哈夫曼编码原理与应用详解

本文是先用实例进行的简单说明，详细解释在标题6

1.首先简单说一下什么是哈夫曼编码？

例如：我们需要存储一个字符串aaaaaabbbbbqqqwwe，因为这个字符串有17个，所以我们需要14个字节来存储。那我们能进一步减少存储的空间呢？哈夫曼编码就可以解决这个问题

2.那哈夫曼编码的原理是什么呢？

我们直接使用实例来解释

就上面的字符串来举例。我们先统计一下上面每个字符出现的个数

a：6

b：5

q：3

w：2

e：1

下面我们需要构建一个哈夫曼树，构建的规则是：每次取出字符个数最小的两个，构建它们的父节点为它们的个数之和，再依次往复；

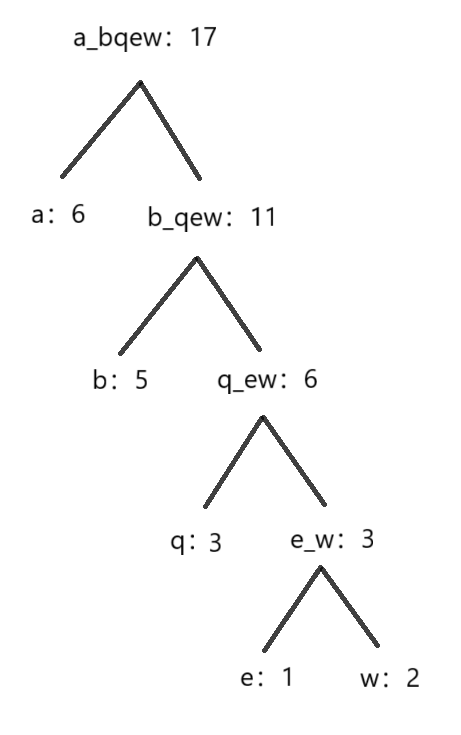
3.编码过程

从根节点开始，向左分支标记0，向右分支标记1

得到的每个字符的编码：

a：0

b：10

q：110

e：1110

w：1111

原字符串aaaaaabbbbbqqqwwe

编码结果0 0 0 0 0 0 10 10 10 10 10 110 110 110 1111 1111 1110

去处空格得到0000001010101010110110110111111111110，相比于原来的17*8=136，比特位少了很多

4.解码过程

编码序列：0 0 0 0 0 0 10 10 10 10 10 110 110 110 1111 1111 1110

使用哈夫曼树解码：

1.读入第一个比特 0 → 从根节点向左 → 到达a

2.读入10→从根节点向右→从根节点向左→到达b

3.依次类推

5.哈夫曼oj题

哈夫曼编码_牛客题霸_牛客网https://www.nowcoder.com/practice/4c0419eb07c840ca8402e4f2a52cfd49?tpId=308&tqId=40489&ru=/exam/oj

cpp 复制代码

#include <functional>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;

int main() {
    int n;
    cin >> n;
    long long sum = 0;
    priority_queue<long long, vector<long long>,greater<long long>> heap;
    while(n--)
    {
        long long x;
        cin >> x;
        heap.push(x);
    } 
    while(heap.size() > 1)
    {
        long long top1 = heap.top();
        heap.pop();
        long long top2 = heap.top();
        heap.pop();
        heap.push(top1+top2);
        sum = sum +top1 + top2;
    }
    cout << sum;

}
// 64 位输出请用 printf("%lld")

6详细原理解释

哈夫曼编码（Huffman Coding） 是一种经典的无损数据压缩算法 ，由大卫·哈夫曼（David A. Huffman）于1952年提出。它的核心思想是根据字符出现的频率来构建最优的变长编码，使得出现频率高的字符用较短的编码表示，出现频率低的字符用较长的编码表示，从而实现数据压缩。

特点

最优前缀码：没有任何编码是其他编码的前缀，解码时无歧义。
贪心算法：通过局部最优选择（每次合并频率最小的节点）达到全局最优。
压缩效率：对于非均匀分布的数据（某些字符频繁出现），压缩效果好；但对均匀分布数据（如加密后数据）效果有限。
需存储编码表：解码时需要哈夫曼树或编码表，会占用少量额外空间。

应用场景

文件压缩（ZIP、GZIP、PNG图像等）
通信协议中的数据压缩
多媒体编码（如JPEG、MP3中结合其他技术）

局限性

需要预先统计频率（或两遍扫描：第一遍统计，第二遍编码）。
对于小数据量，存储编码表的开销可能抵消压缩收益。
无法适应动态变化的数据流（但可通过动态哈夫曼编码改进）。

扩展

自适应哈夫曼编码：在数据流中动态更新频率和树结构，适用于实时压缩。
与算术编码结合：在更复杂的压缩算法中作为组成部分。

哈夫曼编码是信息论和数据结构中的经典算法，体现了用频率换空间的思想，是理解数据压缩的基石之一。