完整的PID和LQR四旋翼无人机simulink,matlab仿真，两个slx文件一个m文件...

完整的PID和LQR四旋翼无人机simulink,matlab仿真，两个slx文件一个m文件，有一篇资料与其对应学习。

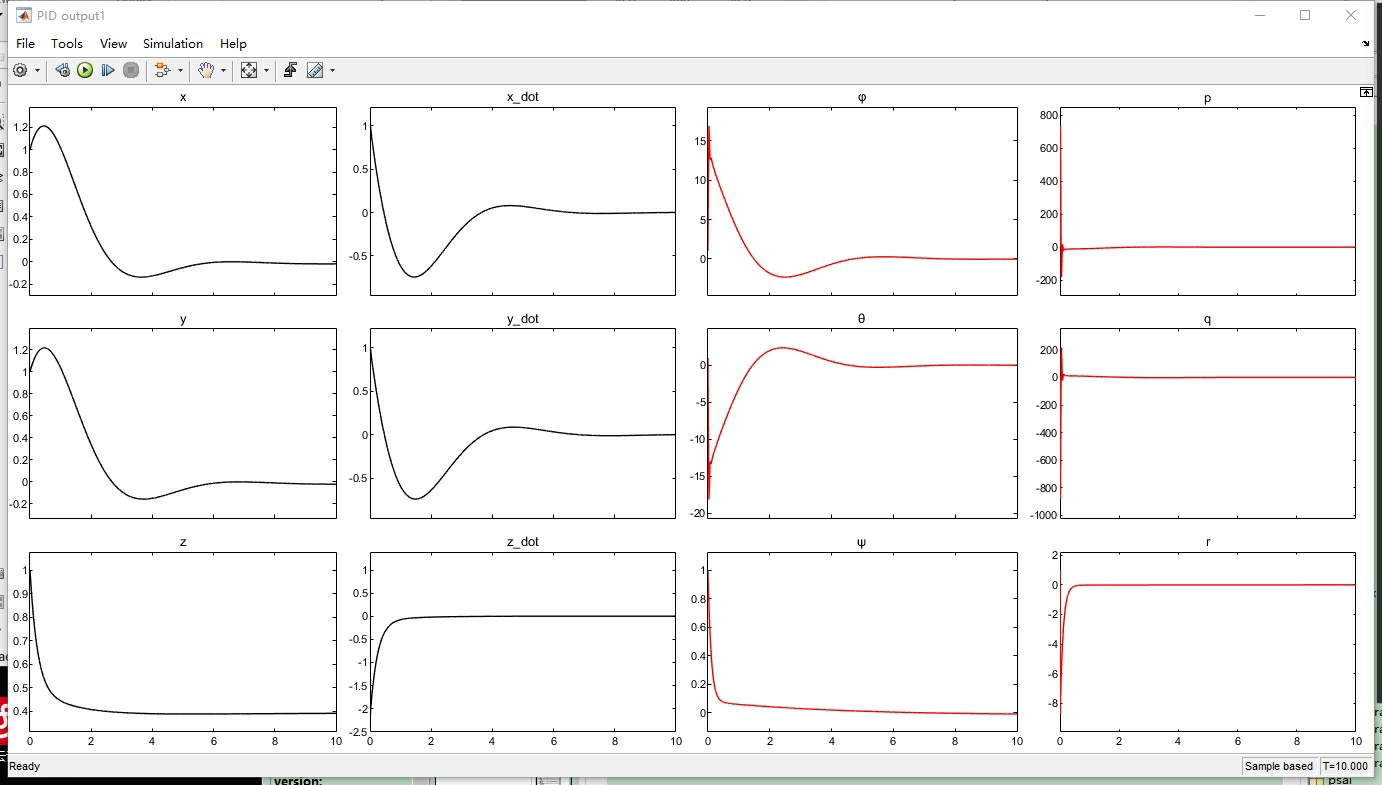
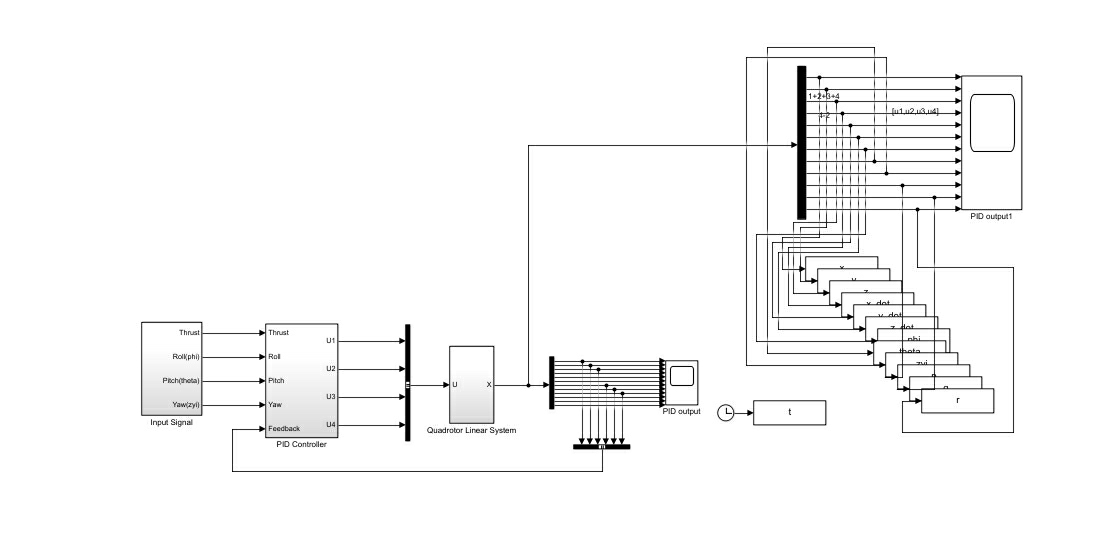
四旋翼控制算法仿真这玩意儿，说难不难说简单也不简单。最近在Matlab里搭了个包含PID和LQR两种控制方案的仿真框架，两个Simulink模型共用同一个动力学模型，参数配置都放在m文件里。先说PID控制那个slx文件，打开就能看到四个环形嵌套的控制器结构------这可不是为了好看，每个环对应姿态角、角速度、位置和速度四个控制维度。

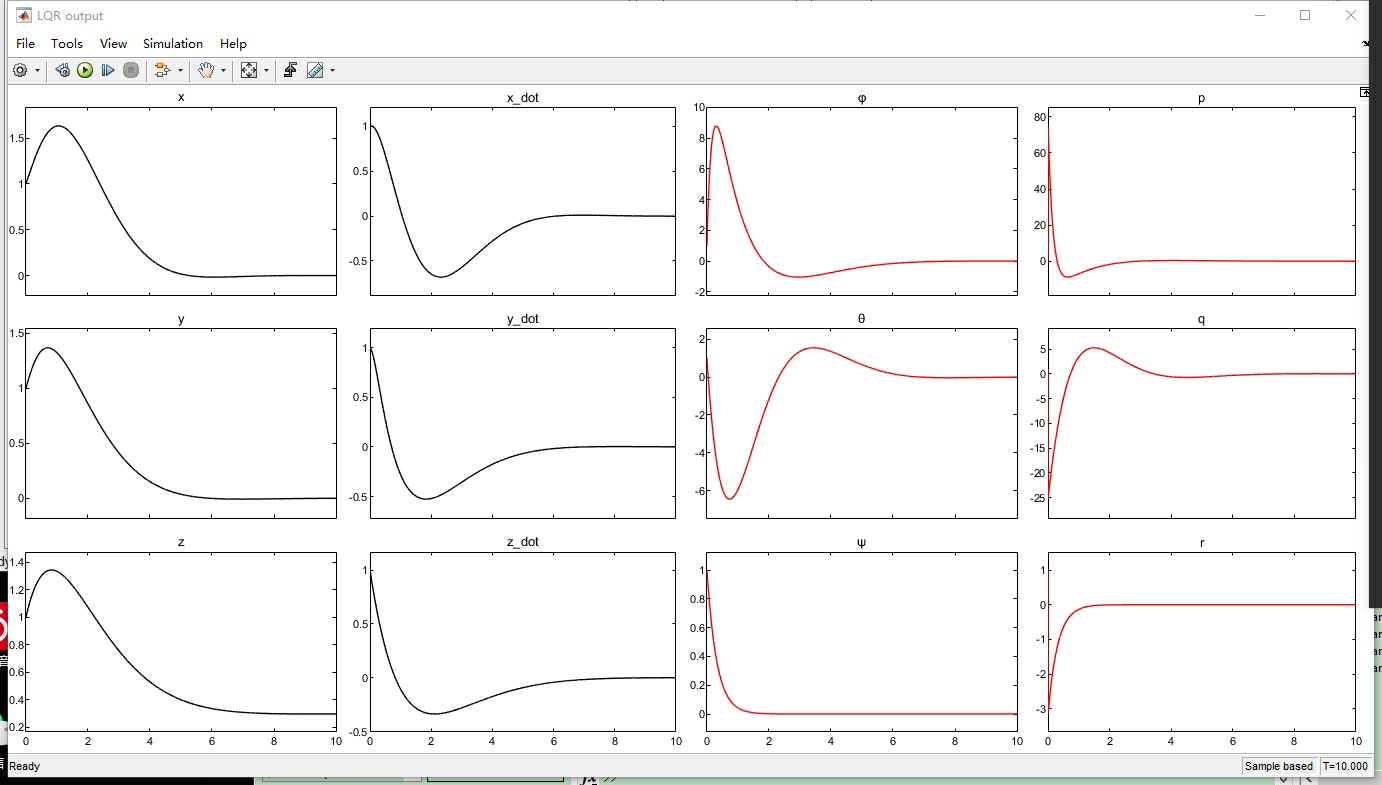
调PID参数那会儿真是试到怀疑人生，特别是积分项。后来在m文件里搞了个参数矩阵批量测试：

matlab 复制代码

Kp_roll = [0.8 1.2 1.5];
Ki_roll = [0.05 0.1];
for i=1:3
    for j=1:2
        simOut = sim('Quadcopter_PID');
        record_data(:,:,i,j) = simOut.logsout{3}.Values.Data;
    end
end

这段循环把三个P值和两个I值排列组合跑仿真，最后用曲面图找最优解。有意思的是当P值超过1.5之后，系统响应反而变慢------后来发现是执行器饱和导致的非线性问题。

LQR那边就是另一个画风了。动力学模型线性化后得到的状态矩阵A长得像被轰炸过的战场：

text 复制代码

A = [0   1   0    0    0    0;
      0   0  -9.8  0    0    0;
      0   0   0    1    0    0;
      0   0   0    0    0    0;
      0   0   0    0    0    1;
      0   0   0    0    0    0];

设计Q矩阵时给高度控制加了10倍权重，结果姿态控制抖得跟筛糠似的。后来改用分块对角矩阵加权，姿态误差项和位置误差项分开处理才算稳住。

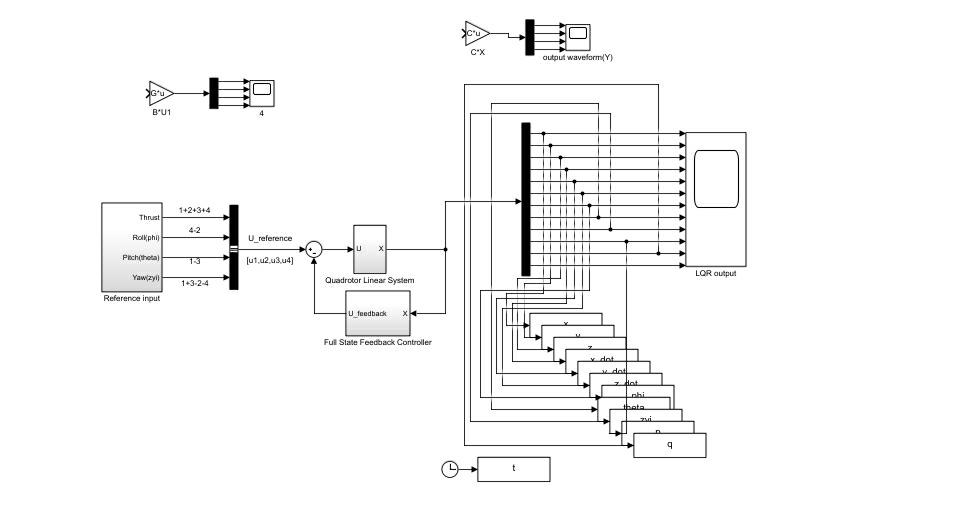
仿真时发现个有趣现象：PID在突加干扰时恢复更快，但稳态误差总在±0.1米晃悠；LQR的轨迹平滑得像德芙巧克力，不过计算量大了三倍。后来在slx里把两种控制器输出并联，用switch模块做实时切换，意外发现过渡过程比单一控制器还稳定------这可能就是玄学吧。

最后说说那个m文件里的数据记录功能，用To Workspace模块导出的数据结构比俄罗斯套娃还复杂。写了个解析函数把嵌套的timeseries数据转成三维数组，这才搞定误差统计分析。建议新手别在数据命名上玩花样，保持time、state、input这种直男命名最省事。