2025.9.24华为软开

1.环形粒子加速器的能量校准

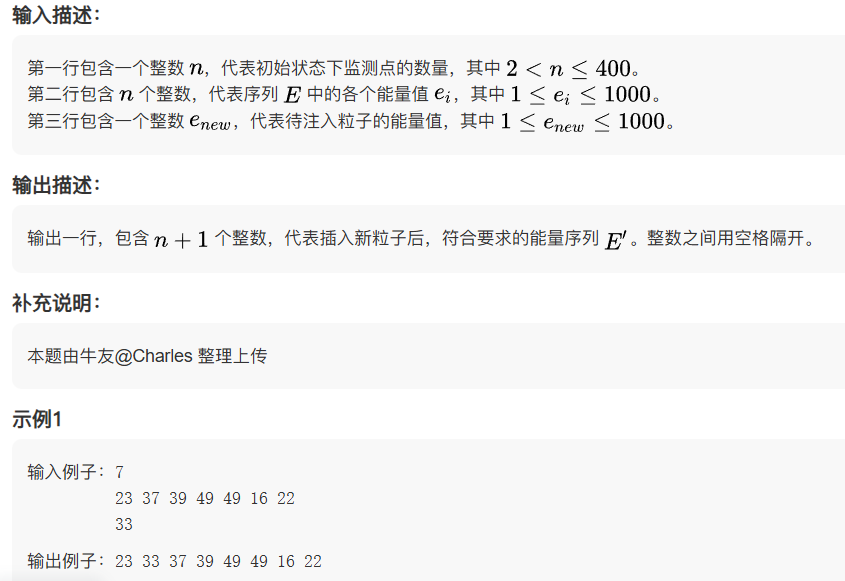
枚举每一个位置

java 复制代码

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class Main {
    /**
     * 求列表中断点（环形非递减序列中出现递减断点的个数）的数量是不是等于1
     * @param list
     * @return
     */
    private static boolean isValid(List<Integer> list) {
        int cutCount = 0;
        for (int i = 0; i < list.size(); i++) {
            int curNum = list.get(i);
            int nextNum = list.get((i + 1) % list.size());
            if (curNum > nextNum) {
                cutCount++;
            }
        }
        return cutCount == 1;
    }
    public static void main(String[] args) {
        //1.初始化输入列表
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        List<Integer> list = new ArrayList<>(n);
        for (int i = 0; i < n; i++) {
            list.add(scanner.nextInt());
        }
        //2.枚举每一个位置插入数字看是否满足环形单调非递减
        int newNum = scanner.nextInt();
        List<Integer> newList = new ArrayList<>(list);
        for (int i = 0; i <= n; i++) {
            newList.add(i, newNum);
            if (isValid(newList)) {
                break;
            }
            newList.remove(i);
        }
        //3.如果新列表的大小没有变说明没有满足要求的位置插入，那么说明所有的数字都一样，插入的数据也是一样的
        if (newList.size() == list.size()) {
            newList.add(0, newNum);
        }
        //4.输出结果
        for (Integer i : newList) {
            System.out.print(i + " ");
        }
        scanner.close();
    }
}

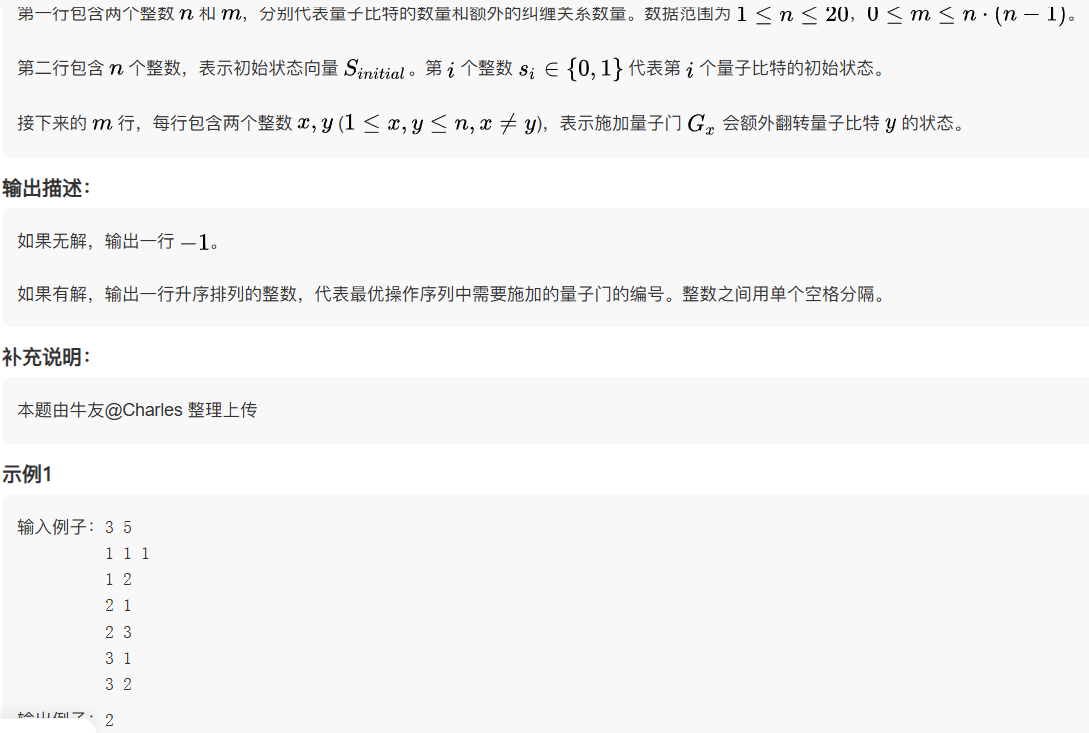
2.量子门

java 复制代码

import java.util.*;

public class Main {
    private static int n;
    private static int[] mask; // mask[1..n] 对应每个操作的翻转向量
    private static int target; // 目标状态对应的mask（初始状态向量）
    private static boolean found = false;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        int m = sc.nextInt();

        int[] s = new int[n];
        for (int i = 0; i < n; i++) {
            s[i] = sc.nextInt();
        }

        // 初始化每个操作的mask：必定翻转自身
        mask = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            mask[i] = 1 << (i - 1); // 第i个操作翻转第i-1位（二进制）
        }

        // 处理纠缠关系
        for (int i = 0; i < m; i++) {
            int x = sc.nextInt();
            int y = sc.nextInt();
            mask[x] |= 1 << (y - 1); // Gx翻转y对应的位
        }

        // 计算目标mask（初始状态需要被抵消的向量）
        target = 0;
        for (int i = 0; i < n; i++) {
            if (s[i] == 1) {
                target |= 1 << i;
            }
        }

        // 按操作数量从小到大枚举（0到n）
        for (int k = 0; k <= n; k++) {
            if (found) break;
            // 回溯生成k个操作的组合（升序，保证字典序）
            backtrack(1, new ArrayList<>(), 0, k);
        }

        // 无解情况
        if (!found) {
            System.out.println(-1);
        }
        sc.close();
    }

    /**
     * 回溯生成组合
     * @param start 起始操作编号（避免重复，保证升序）
     * @param path 当前组合路径
     * @param current 当前异或和
     * @param k 需要选的操作数量
     */
    private static void backtrack(int start, List<Integer> path, int current, int k) {
        if (found) return;
        if (path.size() == k) {
            if (current == target) {
                // 输出结果
                for (int i = 0; i < path.size(); i++) {
                    if (i > 0) System.out.print(" ");
                    System.out.print(path.get(i));
                }
                found = true;
            }
            return;
        }

        // 剪枝：剩余可选数不够k-path.size()时跳过
        for (int i = start; i <= n && (n - i + 1) >= (k - path.size()); i++) {
            path.add(i);
            backtrack(i + 1, path, current ^ mask[i], k);
            path.remove(path.size() - 1); // 回溯
            if (found) return;
        }
    }
}

3.虫洞网络

问题分析

这道题本质是最短路径问题 ，需要将 "虫洞网络" 建模为图的节点，利用Dijkstra 算法求解最小能量消耗。核心逻辑是：进入虫洞网络需支付成本，网络间通过共享星系连通，目标是找到从起始星系所属网络到包含目标星系网络的最小成本路径。

解题思路

建模转化：
- 将每个虫洞网络视为图的节点，节点权重为进入该网络的成本。
- 若两个网络共享星系，则它们之间有边，边权重为目标网络的进入成本。
- 起始星系所属的网络初始化为可达（成本为该网络的进入成本），目标是找到包含目标星系的网络的最小成本。
预处理：
- 记录每个星系所属的虫洞网络（方便快速查找连通性）。
- 构建虫洞网络的邻接表（哪些网络与当前网络共享星系）。
最短路径求解：
- 使用 Dijkstra 算法（优先队列）计算从起始星系所属网络到其他网络的最小成本。
- 若某个网络包含目标星系，则其成本即为答案；若无可达网络包含目标星系或成本超总能量，输出 - 1。

java 复制代码

import java.util.*;

public class Main {
    private static final int INF = Integer.MAX_VALUE;
    private static int networkNum;//虫洞数量
    private static int[] costs;//去往编号为i的虫洞消耗的能量
    private static List<Set<Integer>> networks;//编号为i的虫洞当中包含的星系编号
    private static Map<Integer, List<Integer>> galaxyToNetworks;//编号为i的星系所在的虫洞编号有哪些

    /**
     * 求解两个虫洞是否相交（两个虫洞是否互连可达）
     * @param set1
     * @param set2
     * @return
     */
    private static boolean hasIntersection(Set<Integer> set1, Set<Integer> set2) {
        for (Integer i : set1) {
            if (set2.contains(i)) {
                return true;
            }
        }
        return false;
    }

    private static void dijkstra(int startGalaxy, int endGalaxy, int limit) {
        //0.如果起始星系或者终点星系根本不在任何一个虫洞中，直接返回
        if (galaxyToNetworks.get(startGalaxy) == null || galaxyToNetworks.get(endGalaxy) == null) {
            System.out.println(-1);
            return;
        }
        //1.定义minCost数组，表示达到编号i的虫洞最少的能量消耗是多少，初始化为无穷大表示不可达消耗的能量无限多
        int[] minCosts = new int[networkNum];
        Arrays.fill(minCosts, INF);
        //2.定义优先队列，依据能量消耗排序的小根堆，类型是长度为2的数组，索引0是要到达的虫洞编号，索引1是消耗的能量
        PriorityQueue<int[]> priorityQueue = new PriorityQueue<>((a, b) -> a[1] - b[1]);
        //3.将顶点可到达的虫洞做初始化
        for (int network : galaxyToNetworks.get(startGalaxy)) {
            minCosts[network] = costs[network];
            priorityQueue.add(new int[]{network, costs[network]});
        }
        //4.贪心求解从起点能到达的虫洞去往其他虫洞的最少能量消耗
        while (!priorityQueue.isEmpty()) {
            int[] cur = priorityQueue.poll();
            //4.1遍历其余虫洞看哪些可达然后更新minCost数组
            for (int i = 0; i < networkNum; i++) {
                if (cur[0] == i) {
                    continue;
                }
                if (hasIntersection(networks.get(cur[0]), networks.get(i))) {
                    if (minCosts[i] > cur[1] + costs[i]) {
                        minCosts[i] = cur[1] + costs[i];
                        priorityQueue.add(new int[]{i, minCosts[i]});
                    }
                }
            }
        }
        //5.找到前往目标星系所在的虫洞需要的最小代价
        int result = INF;
        for (int network : galaxyToNetworks.get(endGalaxy)) {
            result = Math.min(result, minCosts[network]);
        }
        //6.输出结果
        System.out.println(result >= limit ? -1 : result);
    }

    public static void main(String[] args) {
        //1.初始化输入
        Scanner scanner = new Scanner(System.in);
        networkNum = scanner.nextInt();
        int startGalaxy = scanner.nextInt();
        int endGalaxy = scanner.nextInt();
        int limitCost = scanner.nextInt();
        costs = new int[networkNum];
        networks = new ArrayList<>(networkNum);
        galaxyToNetworks = new HashMap<>();
        for (int i = 0; i < networkNum; i++) {
            costs[i] = scanner.nextInt();//跃迁到虫洞i消耗的能量
            int n = scanner.nextInt();//虫洞i包含的星系个数
            Set<Integer> galaxys = new HashSet<>();//虫洞i包含的星系
            for (int j = 0; j < n; j++) {
                int galaxy = scanner.nextInt();
                galaxys.add(galaxy);
                galaxyToNetworks.computeIfAbsent(galaxy, k -> new ArrayList<>()).add(i);
            }
            networks.add(galaxys);
        }
        //2.
        dijkstra(startGalaxy, endGalaxy, limitCost);
        scanner.close();
    }
}

另一种思路

把虫洞看作顶点，里面的各个星系如果可以进入其他星系则视作顶点和顶点联通，以此构造图，最后用floyd算法求解最短路径

java 复制代码

import java.util.*;

public class Main {
    private static final int INF = 50 * 10 + 1;
    private static int vertexNum;
    private static int[][] graph;

    /**
     * 求解两个虫洞是否相交（两个虫洞是否互连可达）
     * @param set1
     * @param set2
     * @return
     */
    private static boolean hasIntersection(Set<Integer> set1, Set<Integer> set2) {
        for (Integer i : set1) {
            if (set2.contains(i)) {
                return true;
            }
        }
        return false;
    }

    private static void floyd(List<Integer> startVertexs, List<Integer> endVertexs, int limit) {
        //1.定义dist数组
        int[][] dist = new int[vertexNum][vertexNum];
        for (int i = 0; i < vertexNum; i++) {
            dist[i] = Arrays.copyOf(graph[i], vertexNum);
        }
        //2.利用floyd求最短路
        for (int k = 0; k < vertexNum; k++) {
            for (int i = 0; i < vertexNum; i++) {
                for (int j = 0; j < vertexNum; j++) {
                    dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
                }
            }
        }
        //3.求所有这些起点到这些终点当中长度最短的那一条
        int result = INF;
        for (int startVertex : startVertexs) {
            for (int endVertex : endVertexs) {
                //3.1如果起点和终点相同那么值为graph[i][i]
                if (startVertex == endVertex) {
                    result = Math.min(result, dist[startVertex][startVertex]);
                }
                //3.2如果起点和终点不同，那么可以知道起点到终点的距离，但是还得加上初始进入起点的代价
                else {
                    result = Math.min(result, dist[startVertex][startVertex] + dist[startVertex][endVertex]);
                }
            }
        }
        //4.输出结果
        System.out.println(result >= limit ? -1 : result);
    }

    public static void main(String[] args) {
        //1.初始化输入
        Scanner scanner = new Scanner(System.in);
        vertexNum = scanner.nextInt();
        int start = scanner.nextInt();
        int end = scanner.nextInt();
        int limit = scanner.nextInt();
        graph = new int[vertexNum][vertexNum];
        for (int i = 0; i < vertexNum; i++) {
            Arrays.fill(graph[i], INF);
        }
        List<Set<Integer>> networks = new ArrayList<>();
        List<Integer> startVertexs = new ArrayList<>();
        List<Integer> endVertexs = new ArrayList<>();
        int[] costs = new int[vertexNum];
        for (int i = 0; i < vertexNum; i++) {
            costs[i] = scanner.nextInt();
            int n = scanner.nextInt();
            Set<Integer> set = new HashSet<>();
            for (int j = 0; j < n; j++) {
                int galaxy = scanner.nextInt();
                if (galaxy == start) {
                    startVertexs.add(i);
                }
                if (galaxy == end) {
                    endVertexs.add(i);
                }
                set.add(galaxy);
            }
            networks.add(set);
        }
        scanner.close();
        //2.利用虫洞之间是否可以通过相交的星系互连可达来创建图
        for (int i = 0; i < vertexNum; i++) {
            for (int j = i; j < vertexNum; j++) {
                if (hasIntersection(networks.get(i), networks.get(j))) {
                    graph[i][j] = costs[j];
                    graph[j][i] = costs[i];
                }
            }
        }
        //3.
        floyd(startVertexs, endVertexs, limit);
    }
}