矢量数据结构能直观地表达地理空间,它能精确地表示实体的空间位置及具有的属性。矢量数据结构处理的空间图形实体是点、线、面和体,它能够方便地进行比例尺变换、投影变换以及图形的输入和输出。
矢量数据的位置、形状表达
空间数据具有一定的位置,矢量数据在表达空间位置时,根据其特征具有不同的维数,不同维数的空间数据表达方式也不同。矢量数据空间位置表达方式如图2-6所示。
1.0维矢量
0维矢量在空间呈点状分布特征,在二维、三维欧氏空间具有特定坐标位置,分别用(X,Y)及(X,Y,Z)来表示,它没有大小和方向,如城镇、气象站、火山口等,主要包括:
实体点(EntityPoint):用来代表一个实体;
注记点(Text Point):用于定位注记;
内点(Label Point):用于负载多边形的属性,存在于多边形内;结点(Node):表示线的终点和起点;
结点(Node):表示线的终点和起点;
角点(Vertex):表示线段和弧段的内部点
2.一维矢量
一维矢量在空间呈线状分布特征,在二维、三维欧氏空间分别用离散化的实数点集(X1.Y1)(X2,Y2)...(Xn,Yn)及(X1,Y1,Z1,)(X2,Y2,Z2)...(Xn,Yn,Zn)来表示.它具有长度、曲率、方向,其长度随比例尺变化。一维实体如河流、海岸线、铁路、公路、地下管线、行政边界等,主要包括:
直线:由起点坐标、终点坐标、属性、显示符等组成;
弧、链、网络:是n个坐标对的有序集合,附有属性、指针系统、显示符号等。
3.二维矢量
二维矢量在空间呈面状分布特征,在二维、三维欧氏平面上是一组闭合弧段所包围的空间区域,有特定坐标位置,分别用(X1,Y1)(X2,Y2)...(Xn,Yn)(X1,Y1)及(X1,Y1,Z1,)(X2,Y2,Z2)...(Xn.,Yn,Zn)(X1,Y1,Z1.)来表示。它具有面积、周长、凹凸性、走向、倾角和倾向等几何特征,其面积、周长等随比例尺变化。二维矢量又称多边形或图斑,在数据库中由一封闭曲线加内点来表示面状实体。二维矢量用来表示岛、湖泊、地块、行政区域等。当用等高线和剖面法表示时,可表达空间曲面。
4.三维矢量
三维矢量在空间呈体状分布特征,有表面积、体积、长度、高度等,含有孤立块或相邻块、断面图与剖面图等。三维体状物体一般具有体积、长度、宽度、高度、空间曲面的面积、空间曲面的周长等属性。
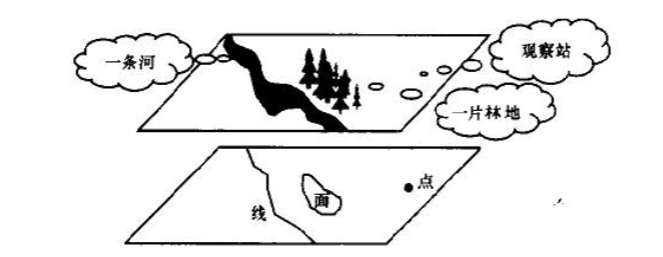
在GIS中,空间数据代表着现实世界地理实体或现象。图2-6为具有一个观察站、一条河和一片林地的区域图及该区域位置形状的矢量数据表达图。其中:
观察站:在空间呈点状分布特征,它具有特定坐标位置,在欧氏平面上用0维实体(X,Y)来表示,其属性信息表示它是一个观察站。
河流:在空间呈线状分布特征,在欧氏平面上用一维矢量表示,由离散化的实数点集(X1,Y1)(X2,Y2)...(Xn,Yn)组成。它具有长度、曲率、水质等属性信息。
林地:在空间呈面状分布特征,在欧氏平面上是一组闭合弧段所包围的空间区域,用(X1,Y1,)(X2,Y2)...(Xn,Yn)(X1,Y1,)来表示。它具有面积、林种组成、畜积等属性信息。
矢量数据的空间关系表达
地理空间信息不仅包含空间几何信息,还包含空间关系信息。空间关系信息主要有空间度量关系、方位关系和拓扑关系,其中空间拓扑关系是最主要的空间关系信息,在GIS数据模型研究中占有十分重要的位置。
1.空间度量关系的表达
空间度量关系描述空间实体之间距离(定量的值、定性的远近),可通过对点、线、面元素的数学表达式计算得到。
2.空间方位关系的表达
空间方位关系分绝对、相对和基于观测者的方位。绝对方位以地球参照系统为标准,如东、西、北、东南等。绝对方位以所给目标为参照方向,如左、右、前、后、上、下等
3.空间拓扑关系的表达
地理要素空间性信息中几何信息其理论基础是几何学(Geometry),它常用空间坐标的位置、方向、角度、距离、面积等描述物体的几何形状和数量特征。拓扑信息是空间关系信息,其理论基础是拓扑学(Topology),拓扑学是几何学的一个分支,它研究的不是具体的几何体的面积、周长、边长、角度,而是将几何体抽象成点、线、面等元素,再研究其间的关系,其表达方式较复杂。
从拓扑的观点看,只关心空间点、线、面之间的逻辑关系,而不关心其几何形状。因此,拓扑信息是一种性能比较稳定的信息,它不受投影关系、比例尺而变化。
1)拓扑学中的空间基本元素
(1)结点(Node):弧段的交点,岛结点是特殊结点。
(2)弧段(Arc):相邻两结点之间的坐标链,岛边界弧段是特殊弧段。
(3)多边形(Polygon)(图斑或面):有限弧段组成的封闭区。
2)拓扑学中空间基本元素的关系及性质
拓扑学中空间基本元素为点、线、面三类,它们之间可归纳为6种关系,关系的性质为关联、相邻、相连、相交、相离、相重、包含等。
(1)点-点间关系:主要指两点间的重合关系和相离关系;
(2)点-线间关系:主要指点和线之间的关联、相交、相离、包含等关系;(3)点-面间关系:主要指点和面间的关联、相交、相离、包含等关系;(4)线-线间关系:主要指二条线间的邻接、相交、相离、相重、包含等关系;
(5)线-面间关系:主要指线和面间的关联、相交、相离、相重、包含等关系;(6)面-面间关系:主要指面和面间的邻接、相交、相离、相重、包含等关系。
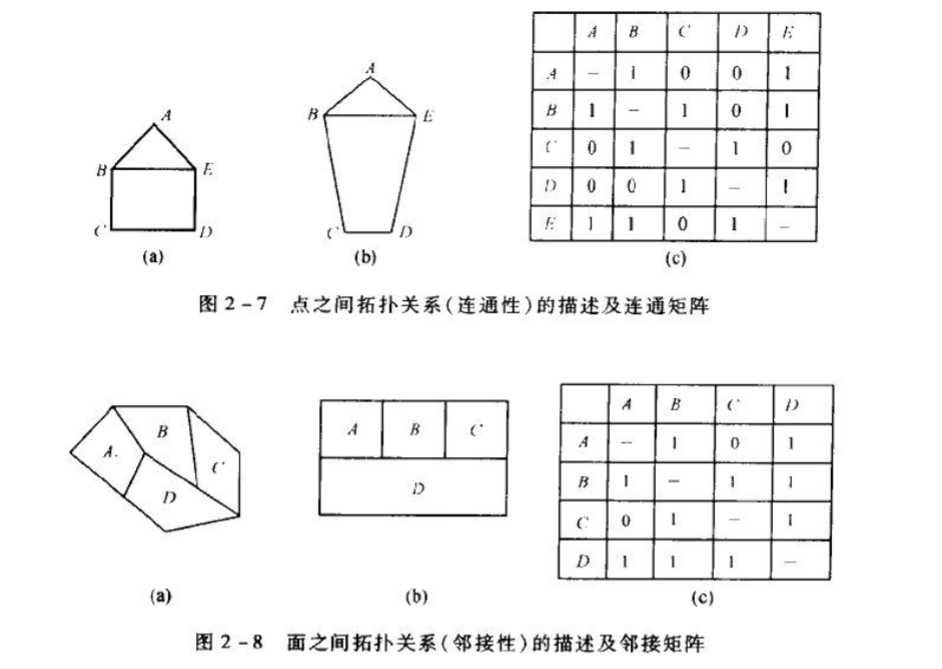
从拓扑角度看,几何形状不同的事物其拓扑关系可能相同。图2-7(a)、(b)描述了两个几何形状不同的实体,但各点之间邻接性关系(点之间邻接性也称连通性)是相同的,都可通过点的邻接矩阵(连通性矩阵)来表示。图2-7(c)中的值1,表示相对应的两点是连通的。
图2-8(a)、(b)描述了两个几何形状不同的实体,但各面之间邻接性关系是相同的,都可通过面邻接矩阵来表示。图2-8(c)中的值1,表示相对应的两个面是邻接的。
3)空间数据的主要拓扑关系的应用
(1)拓扑的关联性
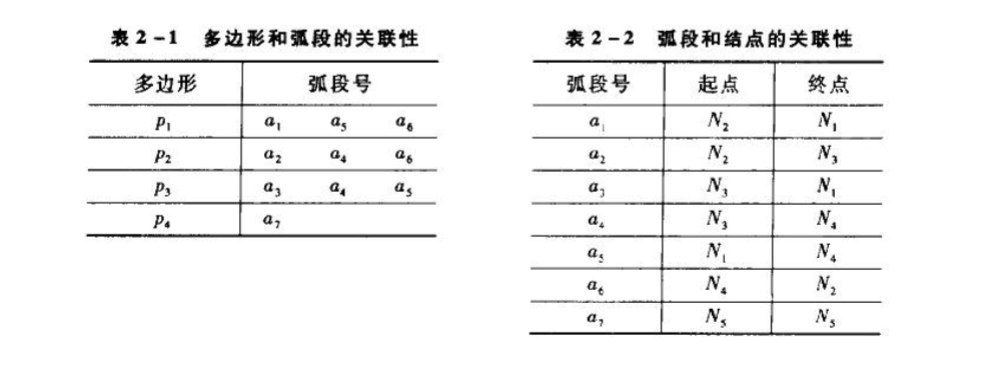
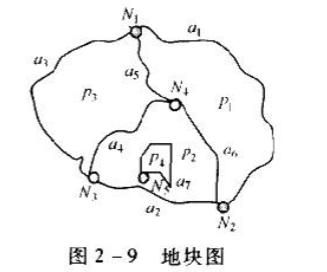
拓扑的关联性表示不同类型元素(结点、弧段、多边形)之间的关系。表2-1和表2-2描述了图2-9地块图的拓扑的关联性。通常,在存储拓扑关系时,拓扑关联性最为重要。
(2)拓扑的邻接性和连通性拓扑的邻接性和连通性
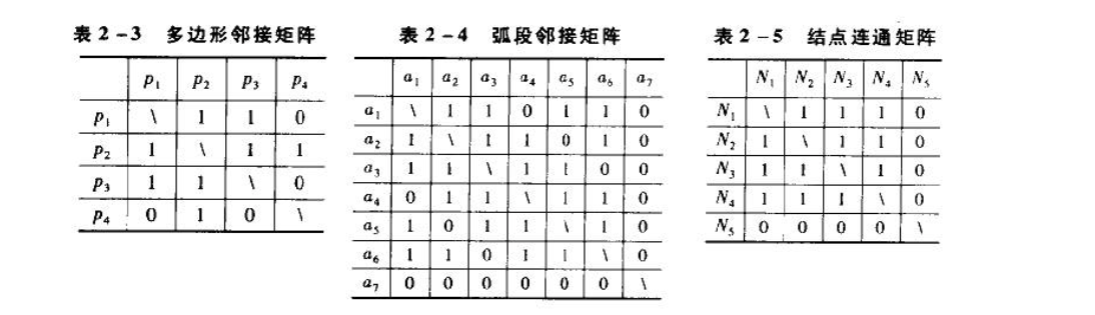
表示同类型元素(结点、弧段、多边形)之间的关系。主要表示多边形之间的邻接性;弧段之间的邻接性;结点之间的连通性。表2-3、表2-4和表2-5分别描述了图2-9地块图的拓扑邻接性和连通性。
(3)拓扑的包含性
拓扑的包含性主要包括面同点、线、面的包含,指一个点、线或面被另一面包含;也包括点和线被另一线包含。图2-10描述了图素之间的拓扑的包含性。

4)拓扑关系的存储
空间数据的拓扑关系是比较复杂的,现有的GIS系统有存储拓扑关系的系统,也有不存储拓扑关系的系统。对无拓扑关系的系统,应用时通过实时操作运算,求解某些拓扑关系。由于求解拓扑关系的操作运算复杂、计算工作量较大、花费时间长,因此,通常有拓扑关系的GIS具有较强的空间分析功能。对于无拓扑关系的GIS,拓扑分析功能往往偏弱。
在空间数据库查询中空间数据拓扑关系中的相邻性、包含性和重叠性被大量应用。如查询一个国家的邻国、查询同废弃物场相邻的地区、查询预测的洪水淹没区内是否有居民点、找出某区域内土厚大于50cm的地区等。
矢量数据的属性表达
空间数据的属性用来描述空间实体的专题特性,常用数值或字符描述,这一点同常规数据库系统相一致。它同常规数据库系统不同之处在于空间数据的属性始终同空间实体图形数据紧密联系在一起。也就是说,空间数据中的属性都对应于某一特定的地理位置。