第3节——differentiation rules（求导法则）

3. 求导法则

求导不是记忆，而是规则 + 组合的艺术。

text 复制代码

3.1 基本求导公式（必须记住）
3.2 加法法则
3.3 乘法法则（Product Rule）
3.4 链式法则（Chain Rule）最重要
3.5 Python 验证 + 可视化
3.6 本节练习

3.1 基本求导公式（记住这 7 条就够了）

函数	导数
ccc	000
xxx	111
xnx^nxn	nxn−1n x^{n-1}nxn−1
exe^xex	exe^xex
ln⁡x\ln xlnx	1/x1/x1/x
sin⁡x\sin xsinx	cos⁡x\cos xcosx
cos⁡x\cos xcosx	−sin⁡x-\sin x−sinx

这 7 条是整个求导体系的基础。

3.2 加法法则

(f+g)′=f′+g′(f+g)'=f'+g'(f+g)′=f′+g′

例：(x2+sin⁡x)′=2x+cos⁡x(x^2+\sin{x})'=2x+\cos{x}(x2+sinx)′=2x+cosx

3.3 乘法法则

乘法法则的本质：两个变量同时变化时，它们的乘积变化需要两部分贡献。
公式：
(fg)′=f′g+fg′(fg)'=f'g+fg'(fg)′=f′g+fg′
记作：前导 × 后 + 前 × 后导
例：(x2sin⁡x)′=2xsin⁡x+x2cos⁡x(x^2\sin{x})'=2x\sin{x}+x^2\cos{x}(x2sinx)′=2xsinx+x2cosx

3.4 链式法则

链式法则负责处理"嵌套结构"。
如果一个函数里面又包着一个函数，就用链式法则。
形式：
ddxf(g(x))=f′(g(x))⋅g′(x)\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)dxdf(g(x))=f′(g(x))⋅g′(x)
记作：外导内不动 × 内导
例 1：(2x+1)5(2x+1)^5(2x+1)5

外：u5u^5u5

内：u=(2x+1)u=(2x+1)u=(2x+1)
5(2x+1)4⋅25(2x+1)^4\cdot 25(2x+1)4⋅2
例 2：sin⁡x2\sin{x^2}sinx2

外：sinsinsin

内：x2x^2x2
cos⁡x2⋅2x\cos{x^2}\cdot 2xcosx2⋅2x
例 3：ln⁡cos⁡x\ln{\cos{x}}lncosx

外：lnlnln

内：cos⁡x\cos{x}cosx
1cos⁡x⋅(−sin⁡x)=−tan⁡x\frac{1}{\cos{x}}\cdot (-\sin{x})=-\tan{x}cosx1⋅(−sinx)=−tanx
链式法则会自动"乘内导"，这是以后做深度学习梯度下降的基础工具。

3.5 用 Python 验证上面做的导数

用 sympy 来检查你的答案

python 复制代码

import sympy as sp

x = sp.symbols('x')

expr = (2*x+1)**5
sp.diff(expr, x)

10(2x+1)4\displaystyle 10 \left(2 x + 1\right)^{4}10(2x+1)4

python 复制代码

expr = sp.sin(x**2)
sp.diff(expr, x)

2xcos⁡(x2)\displaystyle 2 x \cos{\left(x^{2} \right)}2xcos(x2)

3.6 Python 可视化导数（帮助理解链式法则）

例如：
f(x)=sin⁡x2f(x)=\sin{x^2}f(x)=sinx2
f′(x)=2xcos⁡(x2)f'(x)=2x\cos(x^2)f′(x)=2xcos(x2)
绘制：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

xs = np.linspace(-3, 3, 500)
f = np.sin(xs**2)
df = 2*xs*np.cos(xs**2)

plt.plot(xs, f, label='f(x) = sin(x^2)')
plt.plot(xs, df, label="f'(x)")
plt.legend()
plt.show()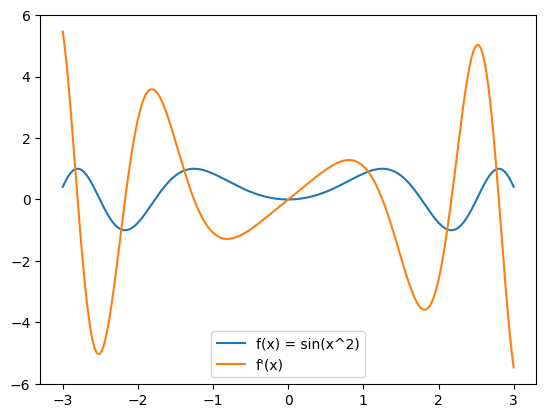

导数的振幅越来越大（因为 2x）

3.7 本节练习

练习 1（加法法则）

求导：
f(x)=x3+5x+sin⁡xf(x) = x^3 + 5x + \sin xf(x)=x3+5x+sinx

解题 1

f′(x)=3x2+5+cos⁡xf'(x)=3x^2+5+\cos{x}f′(x)=3x2+5+cosx

练习 2（乘法法则）

f(x)=x2exf(x) = x^2 e^xf(x)=x2ex

解题 2

f′(x)=2xex+x2exf'(x)= 2xe^x+x^2e^xf′(x)=2xex+x2ex

练习 3（链式法则）

f(x)=(3x−1)4f(x) = (3x - 1)^4f(x)=(3x−1)4

解题 3

f′(x)=4(3x−1)3⋅3f'(x)=4(3x-1)^3\cdot 3f′(x)=4(3x−1)3⋅3

练习 4（重度链式法则）

f(x)=sin⁡(ln⁡(2x+1))f(x) = \sin\left(\ln(2x + 1)\right)f(x)=sin(ln(2x+1))

提示：外 = sin，中 = ln，内 = 2x+1
链式法则会用两次！

解题 4

f′(x)=2cos⁡ln⁡2x+12x+1f'(x)=\frac{2\cos{\ln{2x+1}}}{2x+1}f′(x)=2x+12cosln2x+1

练习 5（链式 + 乘法）

f(x)=x⋅ex2f(x) = x \cdot e^{x^2}f(x)=x⋅ex2

（先视为乘法，再对ex2e^{x^2}ex2用链式）

解题 5

f′(x)=2(x2+1)ex2f'(x)=2(x^2+1)e^{x^2}f′(x)=2(x2+1)ex2