探索弹道计算软件：Matlab GUI 背后的秘密

弹道计算软件由Matlab编写的gui界面有说明文档公式介绍龙格库塔介绍还有多种类似的计算软件

在科研与工程领域，弹道计算是一项关键任务，而弹道计算软件则成为了助力这一任务的强大工具。今天就来聊聊基于 Matlab 编写的弹道计算软件，尤其是其自带的 GUI 界面，简直就是使用者的福音。

Matlab GUI 界面：易用性的提升

Matlab 的 GUI 界面开发功能让弹道计算软件不再是专业人士才能玩转的"高冷"工具。通过直观的图形界面，即使对底层算法不太熟悉的用户，也能轻松上手。例如，我们可以通过简单的按钮、滑块和文本框，实现参数输入与结果查看。

matlab 复制代码

% 创建一个简单的 GUI 按钮
fig = uifigure('Name', '弹道计算界面');
btn = uibutton(fig, 'push',...
    'Text', '开始计算',...
    'Position', [100 100 100 22],...
    'ButtonPushedFcn', @(btn,event)disp('计算开始'));

在这段代码里，我们首先创建了一个名为 "弹道计算界面" 的 uifigure，这就是我们 GUI 的主窗口。接着，创建了一个按钮，设置其文本为 "开始计算"，位置在 [100 100 100 22] （这个位置决定了按钮在窗口中的显示位置，前两个数是坐标，后两个数分别是按钮的宽度和高度），并且定义了按钮按下时的回调函数，这里简单地在命令行显示 "计算开始"。实际应用中，这个回调函数就可以调用弹道计算的核心算法。

说明文档与公式介绍：知其然，更知其所以然

这款软件贴心地配备了说明文档，详细介绍了弹道计算所涉及的公式。这些公式是弹道计算的理论基石，比如经典的运动学方程：

\[ x = v_0 \cos(\theta) t \]

\[ y = v_0 \sin(\theta) t - \frac{1}{2} g t^2 \]

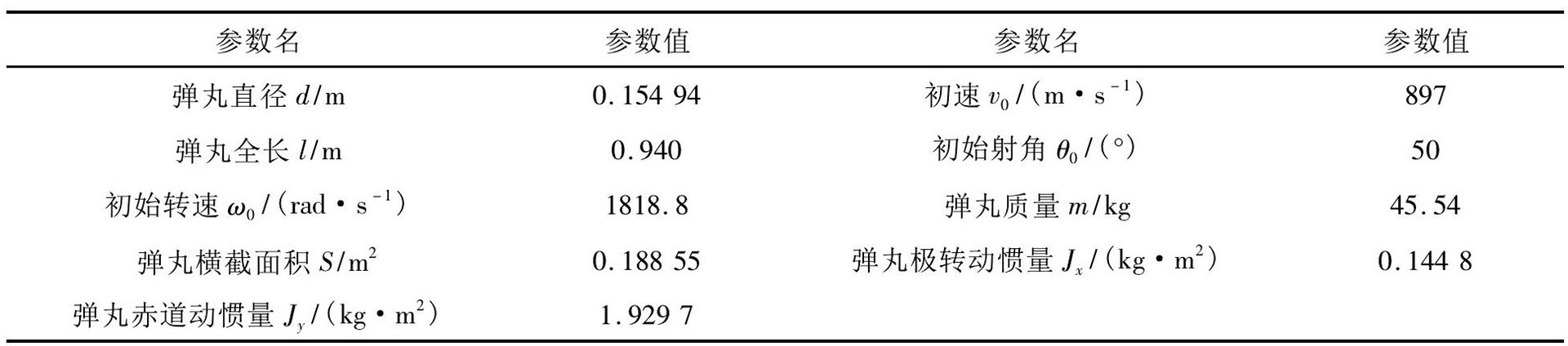
在 Matlab 代码中实现这些公式就非常直观：

matlab 复制代码

% 假设初始速度 v0，发射角度 theta，重力加速度 g
v0 = 100; % m/s
theta = deg2rad(45); % 转换为弧度
g = 9.81; % m/s^2
t = 0:0.01:10; % 时间范围

x = v0 * cos(theta) * t;
y = v0 * sin(theta) * t - 0.5 * g * t.^2;

figure;
plot(x, y);
xlabel('水平距离 (m)');
ylabel('垂直距离 (m)');
title('弹道轨迹');

这段代码中，我们先设定了初始参数，然后根据公式计算出水平和垂直方向的位置随时间的变化。最后使用 Matlab 的绘图函数 plot 绘制出弹道轨迹。通过这样的代码和公式结合，我们就能清楚看到理论是如何在程序中实现的。

龙格 - 库塔介绍：高精度计算的秘诀

龙格 - 库塔方法在弹道计算中起着举足轻重的作用，尤其是对于处理复杂的动力学方程。它是一种数值求解常微分方程的高效算法。以四阶龙格 - 库塔方法为例，对于一个常微分方程 \(\frac{dy}{dt} = f(t, y)\)，其迭代公式为：

\[ k1 = h f(tn, y_n) \]

\[ k2 = h f(t n + \frac{h}{2}, yn + \frac{k1}{2}) \]

\[ k3 = h f(t n + \frac{h}{2}, yn + \frac{k2}{2}) \]

\[ k4 = h f(t n + h, yn + k3) \]

\[ y*{n+1} = y* n + \frac{1}{6}(k1 + 2k 2 + 2k3 + k4) \]

在 Matlab 中实现四阶龙格 - 库塔算法求解简单的常微分方程 \(\frac{dy}{dt} = -y\)，代码如下：

matlab 复制代码

function [t, y] = runge_kutta_4th(f, tspan, y0, h)
    t = tspan(1):h:tspan(2);
    y = zeros(length(t), length(y0));
    y(1, :) = y0;

    for n = 1:length(t)-1
        k1 = h * feval(f, t(n), y(n, :));
        k2 = h * feval(f, t(n) + h/2, y(n, :) + k1/2);
        k3 = h * feval(f, t(n) + h/2, y(n, :) + k2/2);
        k4 = h * feval(f, t(n) + h, y(n, :) + k3);
        y(n+1, :) = y(n, :) + (k1 + 2*k2 + 2*k3 + k4)/6;
    end
end

% 定义微分方程
f = @(t, y) -y;
tspan = [0 5]; % 时间区间
y0 = 1; % 初始条件
h = 0.01; % 步长

[t, y] = runge_kutta_4th(f, tspan, y0, h);
figure;
plot(t, y);
xlabel('时间 t');
ylabel('y 的值');
title('四阶龙格 - 库塔法求解 \frac{dy}{dt} = -y');

在这个代码中，我们定义了一个四阶龙格 - 库塔算法的函数 rungekutta4th，它接受微分方程函数句柄 f、时间区间 tspan、初始条件 y0 和步长 h 作为输入。在函数内部，按照龙格 - 库塔公式进行迭代计算。通过这样的实现，我们就能将龙格 - 库塔方法应用到弹道计算中复杂的动力学方程求解上，提高计算精度。

多种类似计算软件：对比与选择

除了这款基于 Matlab 的弹道计算软件，市面上还有多种类似软件。例如，Python 也有不少用于科学计算与可视化的库，像 SciPy 库中的 odeint 函数，也可以用于求解常微分方程，实现弹道计算。不同软件各有优缺点，Matlab 胜在其丰富的工具箱和简单易懂的语法，适合初学者和快速开发；而 Python 则以其开源特性和强大的社区支持，在数据处理和算法优化方面有独特优势。具体选择哪种软件，要根据实际需求，如计算精度要求、开发成本、团队技术栈等因素来综合考虑。

总之，弹道计算软件无论是对于军事研究、航天工程还是其他相关领域，都有着不可替代的作用。深入了解这些软件背后的原理和实现，能帮助我们更好地利用它们来解决实际问题。