排序的概念
排序,就是把杂乱无章的数据变得"井井有条"的过程。它依据特定规则(如数字大小、字母顺序),将一组数据重新排列,是计算机处理信息、提升查找和分析效率的基础操作。
一般用于购物平台等。
对于排序算法来说有时间,空间和稳定性3个方面。
时间,是执行次数的多少。
空间是额外开辟空间的大小。
稳定性是相同元素的比较
常见的排序算法
插入排序
时间复杂度o(N*N)到o(N),比冒泡号
空间O(1);
稳定性:稳定
把数插入一个一个有序的数组。
原理arr={1,3,4,7,8},n=5.
arr={1,3,4,7, ,8}
arr={1,3,4, ,7,8}
arr={1,3,4,5,7,8}
cpp
void pai(int* arr, int n) {
for (int i = 0; i < n - 1; i++) {
int end=i;
int tmp = arr[end + 1];
while (end >= 0) {
if (arr[end] > tmp) {
arr[end + 1] = arr[end];
--end;
}
else {
break;
}
}
arr[end+1] = tmp;
}
}
int main(){
int a[10] = { 0,3,2,4,5,7,8,9,1,6,};
pai(a, 10);
int i;
for (i = 0; i < 10; i++) {
printf("%d ", a[i]);
}
return 0;
}
冒泡排序
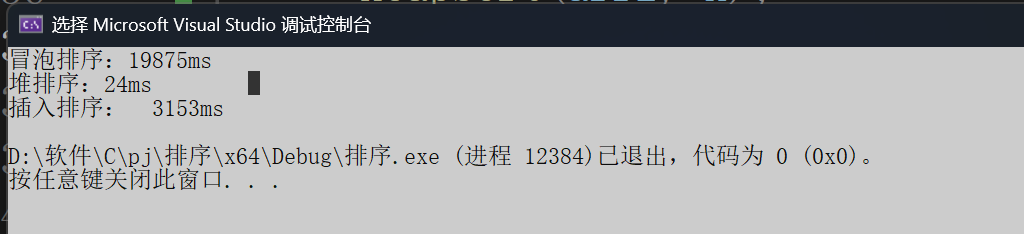
时间复杂度o(N*N)到o(N),趋于o(N*N);
空间复杂度O(1);
稳定性:稳定,
cpp
void maopao(int* arr, int n) {//遍历数组
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1])//大的放在后
{
int t = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = t;
}
}
}
}堆排序
时间O(n log n)
空间O(1)
稳定性:不稳定
cpp
void sw(int* p1, int* p2) {
int t = *p1;
*p1 = *p2;
*p2 = t;
}
void heapify(int* a, int n, int i) {
int largest = i; // 初始化最大值为根
int left = 2 * i + 1; // 左子节点
int right = 2 * i + 2; // 右子节点
// 如果左子节点存在且大于根
if (left < n && a[left] > a[largest])
largest = left;
// 如果右子节点存在且大于当前最大值
if (right < n && a[right] > a[largest])
largest = right;
// 如果最大值不是根节点,则交换并继续调整
if (largest != i) {
sw(&a[i], &a[largest]);
heapify(a, n, largest);
}
}
void heapSort(int* a, int n) {
// 构建最大堆(从最后一个非叶子节点开始向上调整)
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(a, n, i);
}
// 逐个提取堆顶元素(最大值)放到数组末尾
for (int i = n - 1; i > 0; i--) {
sw(&a[0], &a[i]); // 将当前最大值移到末尾
heapify(a, i, 0); // 重新调整堆(堆大小减1)
}
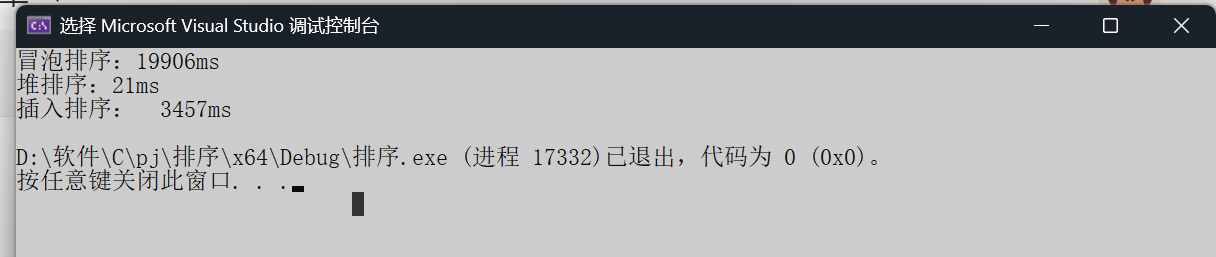
}三个的比较
希尔排序
先进行跨度k的排序,直到k=1进行插入排序;
预排序使数组接近于有序,减少排的时间。
本来插入排序时,100个数时,最坏的情况下第一个数最大,要移99次;
预排序时k=10,最大的数移到末尾只需要10次了;
把个数加多,差距越大。
最后进行插入排序,变得有序
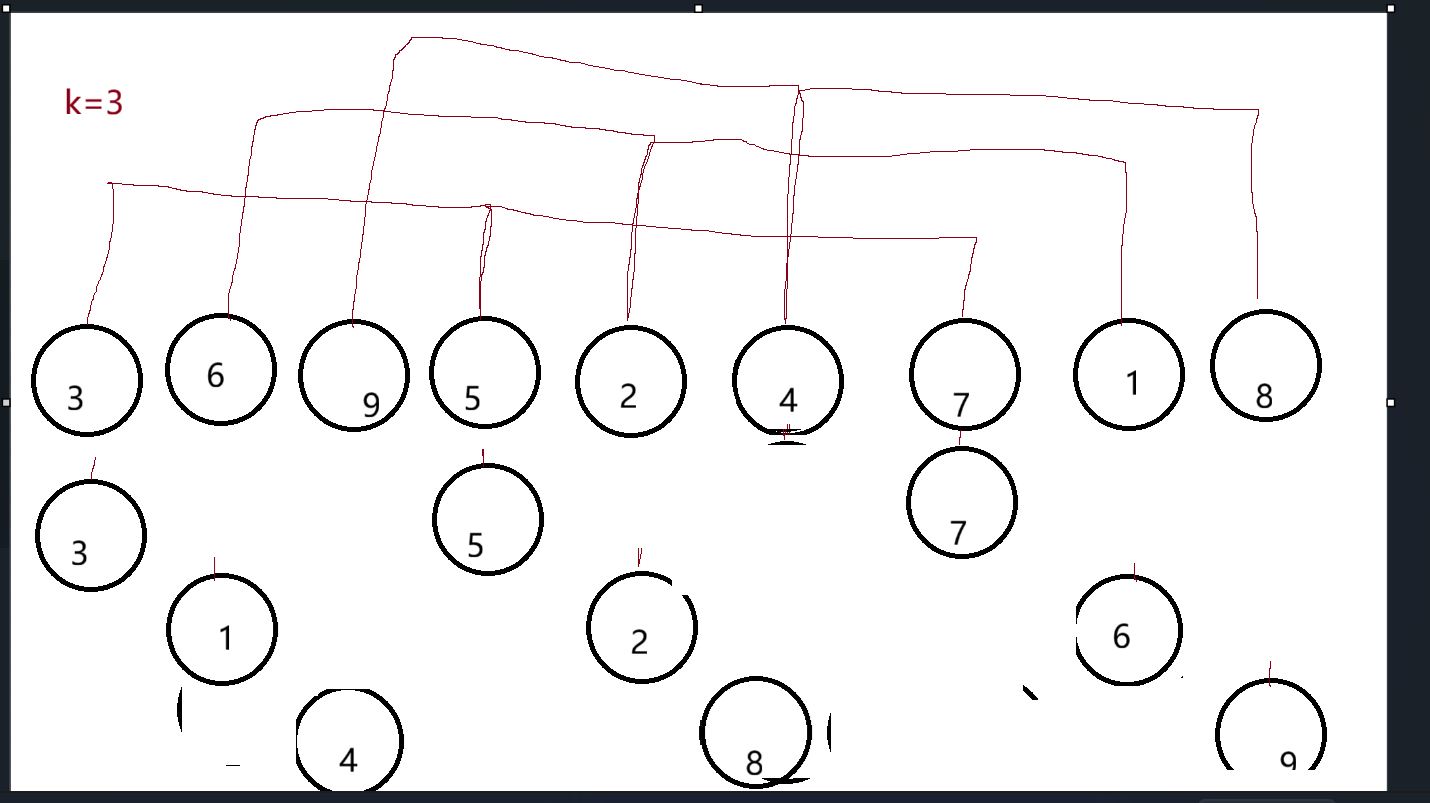
实现
cpp
void xrpai(int* a, int n) {
int k = n;
while (k>1) {
k = k / 3 + 1;//等比缩减间隔
for (size_t j = 0; j < k; j++) {//加快大的移到后面的效率
for (size_t i = j; i < n - k; i += k) {
int end = i;
int tmp = a[end + k];
while (end >= 0) {
if (tmp < a[end]) {
a[end + k] = a[end];
end = end - k;
}
else
break;
}
a[end + k] = tmp;
}
}
}
}时间复杂度是O(N的1.333次方)。
空间复杂度O(1)
稳定性:不稳定
假设第一次是n组,排完后。
第二次是3n组,在n组时已经排序了部分,改变了第二次的环境,组数加多了,但数组有序了一点。
所以次数先增后减。
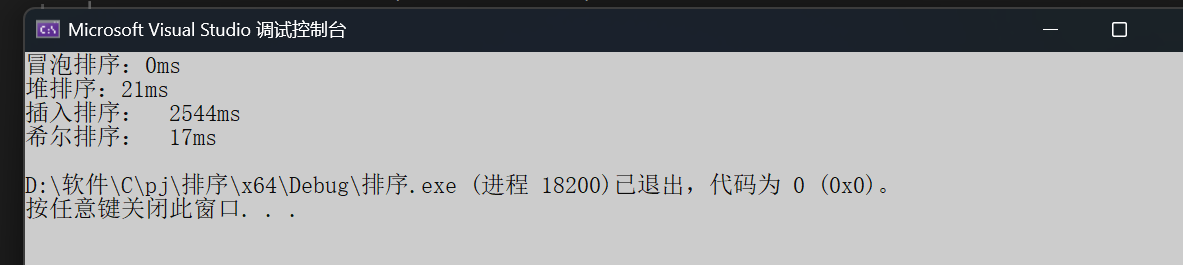
速度比较,和堆排序在一个级别上。
选择排序
选出最小的排在前面再选次小的。
时间复杂度O(N*N)
空间O(1);
稳定性,不稳定
cpp
void xuanpai(int* a, int n) {
int i;
int b = 0;
int end = n-1;
while (end >b) {//所以数据选完
int min = b;
int max = end;
for (i = b + 1; i <= end; i++) {
if (a[min] > a[i]) {
min = i;
}
if (a[max] < a[i])
max = i;
}
int t = a[b];//交换最小位置
a[b] = a[min];
a[min] = t;
if(max==b)//防止max下标的值和min对换
max=min;
t = a[end];//交换最大位置
a[end] = a[max];
a[max] = t;
b++;
end--;
}
}快速排序
霍尔法快速排序
时间复杂度O(N*logN)
空间O(logN)
稳定性:不稳定;
先确定一个数key,一个从左往右找大于key,一个从右往左找小于key,交换找到的值,直到它们相遇。
cpp
#include"插入排序.h"
void sw1(int* p1, int* p2) {
int t = *p1;
*p1 = *p2;
*p2 = t;
}
int getmidi(int* a, int left, int right) {//对于相对有序的优化
int midi = (left + right) / 2;//选出中间的一个数
if (a[midi] > a[left]) {//比较左数
if (a[midi] < a[right]) {//right>midi>ledt
return midi;
}
else if (a[left] < a[right]) {//midi>right>left;
return right;
}
else//midi>left>right
return left;
}
else {//a[left]>=a[midi];
if (a[midi] > a[right])//left>midi>right
return midi;
else if (a[left] < a[right])//right>left>midi
return left;
else//left>right>midi
return right;
}
}
void fastpai(int* a, int left, int right) {
if (left >= right)//只剩一个数
return;
if ((right - left + 1) < 10) {//减少最后递归消耗
pai(a + left, right-left+1);
}
else {
int midi = getmidi(a, left, right);
sw1(&a[left], &a[midi]);
int key = a[left];//选key
int low = left + 1;//选比key大的值
int high = right;//选比key小的值
while (low <= high) {//当low指向越过high
while (low <= high && a[high] >= key) {//选到小的停下
high--;
}
while (low <= high && a[low] <= key) {//选到大的停下
low++;
}
if (low < high) {//low没超过high
sw1(&a[low], &a[high]);//交换使左边比key小,右边比key大
}
}
sw1(&a[left], &a[high]);//到达keyi位置交换
fastpai(a, left, high - 1);//递归key左
fastpai(a, high + 1, right);//递归key右
}
}双指针法快速排序
确定一个key,一个指针找大,一个指针找小。
cpp
void fastpai2(int* a, int left, int right) {
if (left >= right)//只有一个数返回
return;
if ((right - left + 1) < 10) {//少于10个数不递归
pai(a + left, right - left + 1);
}
else {
int midi = getmidi(a, left, right);
sw1(&a[left], &a[midi]);
int keyi = left;//要确定数的位置
int prev = left;//小端
int cur = left + 1;//大的
while (cur <= right) {//到末尾
if (a[cur] < a[keyi] && ++prev != cur)//满足cur选到小才进行执行++prev;
//防止自己交换自己
sw(&a[cur], &a[prev]);//交换大小使小于key的在前
cur++;
}
sw(&a[keyi], &a[prev]);//把key放入;
fastpai2(a, left, prev - 1);//左边
fastpai2(a, prev + 1, right);//右边
}
}挖坑法
选出key,把key变成坑,把右边大的填入左边的坑,把左边大的值填入右坑,直到相等,填入key。
cpp
void fastpai3(int* a, int left, int right) {
if (left >= right)
return;
if ((right - left + 1) < 10) {
pai(a + left, right - left + 1);
}
else {
int midi = getmidi(a, left, right);
sw1(&a[left], &a[midi]);
int key = a[left];
int low = left;
int high = right;
while (low < high) {
// 从右向左找到第一个小于key的元素
while (low < high && a[high] >= key) {
high--;
}
// 将找到的元素填入低指针的位置
a[low] = a[high];
// 从左向右找到第一个大于key的元素
while (low < high && a[low] <= key) {
low++;
}
// 将找到的元素填入高指针的位置
a[high] = a[low];
}
// 最后将基准值放到正确的位置
a[low] = key;
fastpai3(a, left, low - 1);
fastpai3(a, low + 1, right);
}
}非递归快排,防止栈溢出
使用栈来代替递归。
cpp
#pragma once
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int fish;
typedef struct zhan {
fish* x;
int top;
int capacity;
}TP;
void STcs(TP*pst);//初始栈
void STxh(TP*pst);//销毁栈
void STpush(TP*pst,fish x);//入栈
void STpop(TP*pst);//出栈
fish STTop(TP* pst);//取出栈顶
bool STYN(TP* pst);//判断是否为空
int STSize(TP* pst);//个数
void STcs(TP* pst) {//初始栈
assert(pst);
pst->x = NULL;
pst->capacity = 0;
pst->top = 0;
}
void STxh(TP* pst) {//销毁栈
assert(pst);
free(pst->x);
pst->x = NULL;
pst->top = pst->capacity = 0;
}
void STpush(TP* pst, fish x) {//入栈
if (pst->top == pst->capacity) {
int n = pst->capacity == NULL ? 4 : pst->capacity * 2;
fish* tmp = (fish*)realloc(pst->x, sizeof(fish) * n);
if (tmp == NULL) {
perror("malloc fail");
return;
}
pst->x = tmp;
pst->capacity = n;
}
pst->x[pst->top] = x;
pst->top = pst->top + 1;
}
void STpop(TP* pst) {
assert(pst);
assert(pst->top > 0);
pst->top--;
}
fish STTop(TP* pst) {
assert(pst);
assert(pst->top > 0);
return pst->x[pst->top - 1];
}
bool STYN(TP* pst) {
assert(pst);
return pst->top == 0;
}
void print(TP* pst) {
while (!STYN(pst)) {
printf("%d ", STTop(pst));
STpop(pst);
}
}
void fastpai4(int* a, int left, int right) {
TP st;
STcs(&st);
STpush(&st, right);//放入第一个的范围
STpush(&st, left);
while (!STYN(&st)) {//所以数排位
int begin = STTop(&st);//排序第一个范围
STpop(&st);
int end = STTop(&st);
STpop(&st);
int keyi = fastpaid2(a,begin,end);
if (keyi + 1 < end) {//第一个范围的左边
STpush(&st, end);
STpush(&st, keyi + 1);
}
if (begin < keyi-1) {//第二个范围的右边
STpush(&st, keyi-1);
STpush(&st, begin);
}
}
STxh(&st);
}归并排序
时间O(N*logN)
空间O(N);
稳定性:稳定
cpp
#include<stdlib.h>
#include<string.h>
void _guibing(int* a, int* tem, int begin, int end) {
if (begin == end)//只有一个数据返回
return;
int mid = (begin + end) / 2;//划分左右
_guibing(a, tem, begin, mid );
_guibing(a, tem, mid + 1, end);
int begin1 = begin, end1 = mid ;//排序左边
int begin2 = mid + 1, end2 = end;//排序右边
int i = begin;
while (begin1<=end1&&begin2<=end2) {//把左右的数据归在一起排序,直到一边排完
if (a[begin1] < a[begin2]) {
tem[i++] = a[begin1++];
}
else {
tem[i++] = a[begin2++];
}
}
while (begin1 <= end1) {
tem[i++] = a[begin1++];
}
while (begin2 <= end2) {
tem[i++] = a[begin2++];
}
memcpy(a+begin, tem+begin, (end - begin + 1) * sizeof(int));//放回数组
}
void guibing(int* a,int n) {
int* tem = (int*)malloc(sizeof(int) * n);
if (tem == NULL) {
perror("malloc fail");
return;
}
_guibing(a, tem, 0, n );
}非递归
cpp
void guibing2(int* a,int n) {
int* tem = (int*)malloc(sizeof(int) * n);
if (tem == NULL) {
perror("malloc fail");
return;
}
int gap = 1;//gb个数
while (gap < n) {//把所以数据变成两组归并
for (int i = 0; i < n; i += 2 * gap) {//归并2个数
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap , end2 = i + 2 * gap - 1;
if (begin2 >= n) {//没有下一组了
break;
}
if (end2 >= n) {//有下一组但不全
end2 = n - 1;
}
int j = i;
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] < a[begin2]) {
tem[j++] = a[begin1++];
}
else {
tem[j++] = a[begin2++];
}
}
while (begin1 <= end1) {
tem[j++] = a[begin1++];
}
while (begin2 <= end2) {
tem[j++] = a[begin2++];
}
memcpy(a + i, tem + i, (end2 - i + 1) * sizeof(int));
}
gap = gap * 2;//把归并好的数组两两归并
}
free(tem);
tem = NULL;
}非比较排序
只能比较整数
时间o(N+range);对于整数比较快
空间O(range)
#pragma once
//计数排序
#include<stdlib.h>
void jishupai(int* a, int n) {
int i;
int max=a[0];
int min=a[0];
for (i = 0; i < n; i++) {
if (a[i] > max) {
max = a[i];
}
if (a[i] < min)
min = a[i];
}
int range = max - min+1;
int* count = (int*)calloc(range,sizeof(int));
if (count == NULL) {
perror("calloc fail");
return;
}
for (i = 0; i < range; i++) {
count[i] = 0;
}
for (i = 0; i < n; i++) {
count[a[i] - min]++;
}
int t=0;
for (i = 0; i < range; i++) {
while(count[i]--) {
a[t++] = count[i] + min;
}
}
}