前言
🔥个人主页:不会c嘎嘎
📚专栏传送门:【数据结构】 、【C++】 、【Linux】、【算法】、【MySQL】
🐶学习方向:C++方向学习爱好者
⭐人生格言:谨言慎行,戒骄戒躁每日一鸡汤:
"你此刻的每一次咬牙,都是未来闪光的伏笔;别怕路远,只怕你停,别怕梦大,只怕你敢不敢追。把汗水交给今天,把掌声留给明天------当你决定出发,全世界都会为你让路。"


目录
开篇
今天给大家带来三道面试题,分别是:
1.【回文链表 】234. 回文链表 - 力扣(LeetCode) 字节-2024-开发 Meta-2024-开发
2.【最短无序子数组】581. 最短无序连续子数组 - 力扣(LeetCode)字节-2024-开发 谷歌-2024-开发
3.【接雨水】42. 接雨水 - 力扣(LeetCode)字节-2024-开发 腾讯-2024-开发
1.最短无序连续子数组
题目描述
给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。 请你找出符合题意的 最短 子数组,并输出它的长度。
示例 : 输入:
nums = [2, 6, 4, 8, 10, 9, 15]输出:5解释:你需要排序[6, 4, 8, 10, 9],使整个数组变为[2, 4, 6, 8, 9, 10, 15]
核心算法
双指针遍历(贪心思想)
解法思路
我们将数组从逻辑上划分为三段:A (有序) + B (无序) + C (有序)。 我们的目标就是找到 B 段的 左边界 (begin) 和 右边界 (end)。
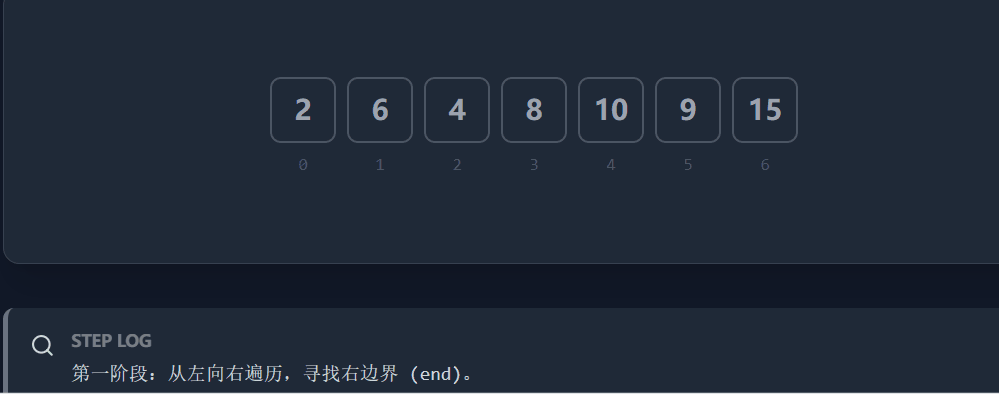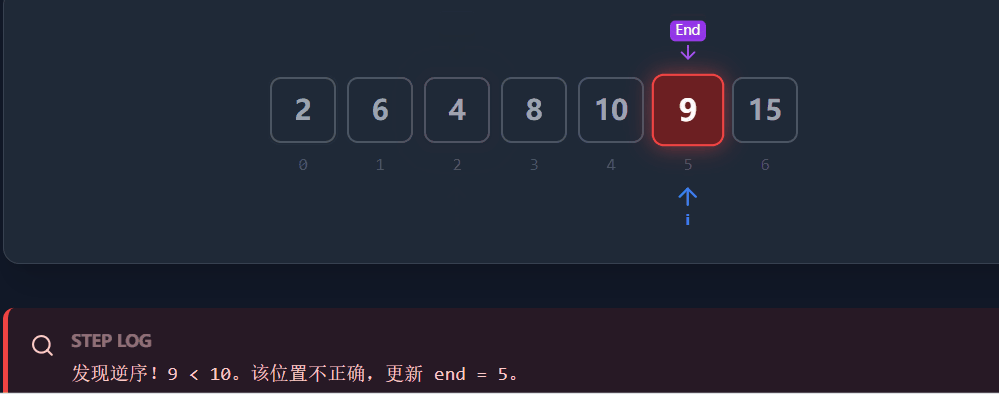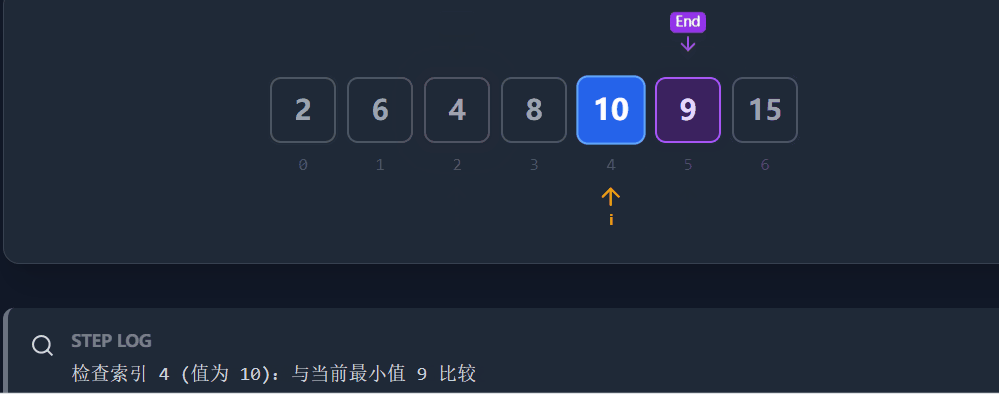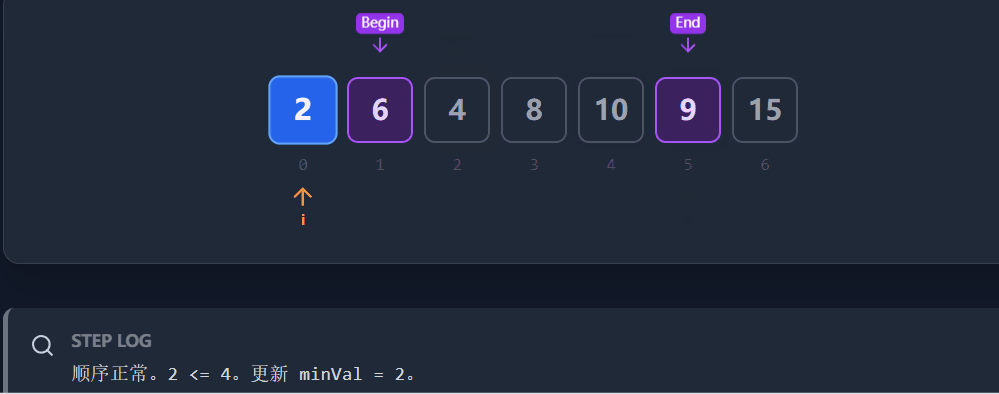
1. 寻找右边界 (end)
原理 :如果数组是整体升序的,那么对于任意位置
i,它一定大于等于左边的所有数(即大于左边的最大值)。操作 :从左向右 遍历。维护一个
maxVal。
如果
nums[i] < maxVal:说明nums[i]的位置不对(它偏小了),它应该属于无序段 B。我们更新end = i。如果
nums[i] >= maxVal:说明当前位置暂时正常,更新maxVal。结论 :遍历结束后,
end记录的就是最右边那个"位置不对"的元素。
2. 寻找左边界 (begin)
原理 :同理,如果数组是整体升序的,对于任意位置
i,它一定小于等于右边的所有数(即小于右边的最小值)。操作 :从右向左 遍历。维护一个
minVal。
如果
nums[i] > minVal:说明nums[i]的位置不对(它偏大了),它应该属于无序段 B。我们更新begin = i。如果
nums[i] <= minVal:说明当前位置暂时正常,更新minVal。结论 :遍历结束后,
begin记录的就是最左边那个"位置不对"的元素。
3. 计算结果
长度
ret = end - begin + 1。边界处理 :如果数组本身就是有序的(例如
[1,2,3]),end和begin可能不会被有效更新(或者end < begin),此时应返回0。
推理流程图
具体代码
cpp
int findUnsortedSubarray(vector<int>& nums)
{
if(nums.size() == 1)
return 0;
int end = 0, maxVal = INT_MIN;
// [2,6,4,8,10,9,15]
//第一次: 正序遍历,找到最后一个值小于我们连续更新的max值的位置
for(int i = 0; i < nums.size(); i++)
{
if(nums[i] >= maxVal)
maxVal = nums[i];
else
end = i;
}
int begin = 0;
int minVal = INT_MAX;
//第二次: 逆序遍历,找到最后一个值大于我们连续更新的min值的位置
for(int i = nums.size() - 1; i >= 0; i--)
{
if(nums[i] <= minVal)
minVal = nums[i];
else
begin = i;
}
int ret = end - begin + 1;
return ret > 1 ? ret : 0;
}2.回文链表
题目描述
给你一个单链表的头节点 head,请你判断该链表是否为回文链表。
-
如果是,返回
true; -
否则,返回
false。
示例 : 输入:
1 -> 2 -> 2 -> 1输出:true
核心算法
快慢指针 + 链表反转
解法思路
判断回文的核心是"两头往中间走"进行比对。但单链表无法从后往前遍历,因此我们需要策略性的改变链表结构:
1.寻找中点
使用快慢指针 fast 和 slow。
slow每次走 1 步,fast每次走 2 步。当
fast走到链表末尾时,slow恰好位于链表的中点(偶数长度时位于下中位数)。
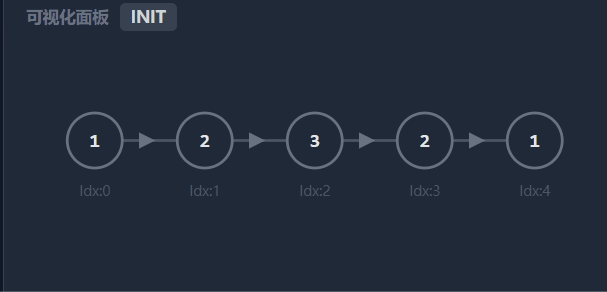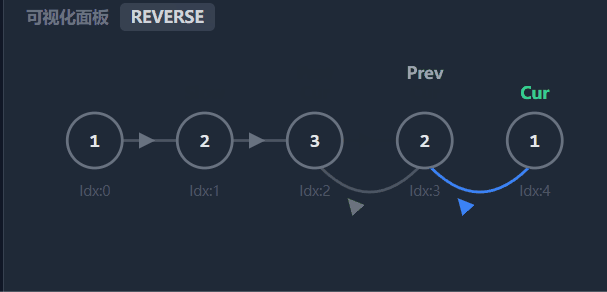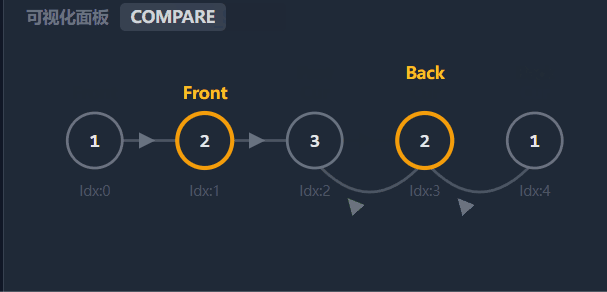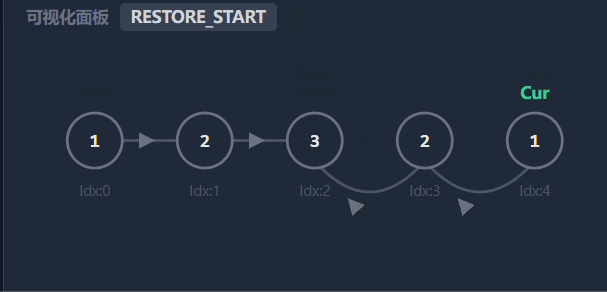
2.反转后半部分
从 slow 位置开始,将后面的链表进行反转。 例如 1 -> 2 -> 3 -> 2 -> 1,反转后变为:
前半部分:
1 -> 2 -> 3(注意:节点 2 仍然指向 3)后半部分(反转后):
1 -> 2 -> 3(3 的 next 变为了 nullptr)
3.比较链表
定义两个指针:
front: 指向原链表头部head。
back: 指向反转后的后半部分头部。
为什么循环条件是 while (back != nullptr)? 这是因为在反转后,原链表的结构变成了一个类似 "Y" 字形 或者 前半部分包含后半部分 的结构。
后半部分链表的尾节点(即原来的中点)指向
nullptr。前半部分的尾节点并没有断开连接,它依然指向中点。
因此,后半部分的长度实际上决定了比较的次数。只要后半部分遍历结束,整个对比就完成了。
4.恢复链表
增加了一个
isPalin标志位。如果在比较过程中发现不相等,不要直接return false,而是先break,执行完恢复链表的操作后再返回结果。
推理流程图
具体代码
cpp
// 辅助函数:反转链表
ListNode* reverseList(ListNode* head) {
ListNode* prev = nullptr;
ListNode* cur = head;
while (cur) {
ListNode* tmp = cur->next; // 保存下一个节点
cur->next = prev; // 反转指向
prev = cur; // 更新 prev
cur = tmp; // 更新 cur
}
return prev;
}
bool isPalindrome(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return true;
}
// 1. 使用快慢指针找中间节点
ListNode* slow = head;
ListNode* fast = head;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
}
// 2. 反转链表后半部分
// slow 此时就是后半部分的头节点
ListNode* backNode = reverseList(slow);
// 保存反转后的头节点,用于后续恢复
ListNode* savedBackHead = backNode;
ListNode* frontNode = head;
// 3. 前半部分正序遍历 和 后半部分反序遍历 比较
bool isPalin = true;
while (backNode != nullptr) {
if (frontNode->val != backNode->val) {
isPalin = false;
break;
}
frontNode = frontNode->next;
backNode = backNode->next;
}
// 4. 恢复链表 (虽然不影响返回值,但保持结构完整是个好习惯)
reverseList(savedBackHead);
return isPalin;
}3.每日温度
前言
在攻克「接雨水」这道 Hard 级别的题目之前,我们先通过「每日温度」来熟悉一个极其重要的解题利器------单调栈。这两道题的核心思想如出一辙,掌握了本题的单调栈用法,再去解决接雨水将事半功倍
题目描述
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1: 输入:
temperatures = [73,74,75,71,69,72,76,73]输出:[1,1,4,2,1,1,0,0]
核心算法
单调栈
解法思路
题目要求我们找到每个元素右边第一个比它大的元素。这是单调栈最经典的应用场景。
我们要维护一个单调递减栈(栈内元素对应的温度从栈底到栈顶逐渐降低):
栈内存什么? 存放数组的下标 (因为我们需要计算天数差
i - st.top())。为什么要递减? 栈里的元素都是"还没有找到比它更高的温度"的日子。一旦遇到一个新的高温,就可以把栈里比这个高温低的元素统统"结算"掉。
1.初始化
创建一个栈
st和结果数组result(默认填充 0)。
2.遍历数组
从左往右遍历温度数组,当前索引为
i。
3.比较与出栈(核心):
如果当前温度
temperatures[i]大于 栈顶索引对应的温度:说明栈顶的那一天终于等到了比它高的温度!此时,执行弹出操作:记录结果
result[top] = i - top,并将栈顶弹出。重复该比较过程,直到栈为空或当前温度不再大于栈顶温度。
4.入栈
将当前索引
i压入栈中,等待后面更高的温度来消除它。
5.后续处理
遍历结束后,栈中剩余的元素说明后面没有比它高的温度了,由于结果数组初始化为 0,无需额外操作。
具体代码
cpp
vector<int> dailyTemperatures(vector<int>& temperatures) {
// 存放下标的栈
stack<int> st;
// 结果数组,初始化为0(默认没有更高温度)
vector<int> result(temperatures.size(), 0);
for(int i = 0; i < temperatures.size(); i++)
{
// 单调栈核心逻辑:
// 当当前温度 > 栈顶所指温度时,说明找到了栈顶元素的"下一个更高温度"
while(!st.empty() && temperatures[i] > temperatures[st.top()])
{
int topIndex = st.top();
st.pop();
// 计算距离(几天后)
result[topIndex] = i - topIndex;
}
// 当前元素入栈,等待寻找它的下一个更高温度
st.push(i);
}
return result;
}4.接雨水
题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
输入 :
height = [0,1,0,2,1,0,1,3,2,1,2,1]输出 :6解释 :上面是由数组[0,1,0,2,1,0,1,3,2,1,2,1]表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。

输入: height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出: 6 **解释:**上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
核心算法
单调栈
解法思路
不同于双指针法的"竖着求"(按列计算),单调栈法的核心思路是"横着求"(按层计算)。 我们要找的是一个凹槽(Bucket)。一个能接水的凹槽,必须具备三个元素:
底(Bottom):当前的凹陷处。
左边界(Left Wall):左边比底高的柱子。
右边界(Right Wall):右边比底高的柱子。
我们需要维护一个单调递减栈 (栈底到栈顶,元素对应的高度递减):
入栈:当当前柱子高度小于等于栈顶高度时,说明我们在"下楼梯",无法形成凹槽,直接入栈(存下标)。
出栈计算 :当
height[i] > height[st.top()]时,说明我们遇到了右边界,形成了一个凹槽,可以开始计算雨水了。
1.遍历与维护递减栈
我们从左到右遍历柱子。如果当前柱子的高度 height[i] 小于等于 栈顶高度,说明我们在"下楼梯",无法形成凹槽的右边。此时直接将下标 i 入栈,这些入栈的元素未来可能会成为凹槽的"左边界"或"底部"。
2.触发计算
确定"底部" 当遇到 height[i] > height[st.top()] 时,说明由于当前柱子变高了,形成了一个右边界 。此时,栈顶元素就是凹槽的底部(mid) 。我们记录并弹出这个底部下标 mid。
3.寻找左边界并计算体积
弹出 mid 后,如果栈变空了,说明左边没有挡板,存不住水,直接结束本次计算。
如果栈不为空,新的栈顶元素就是凹槽的左边界(left)。
此时我们集齐了三要素:左边界(栈顶)、底部(已弹出的mid)、右边界(当前i)。
高
h:木桶效应,取决于左右边界较矮的那个减去底部高度min(height[left], height[i]) - height[mid]宽
w:左右边界下标之间的距离 \\rightarrowi - left - 1累加 :
sum += h * w
4.循环处理与当前元素入栈
因为当前的右边界 i 可能很高,它不仅能和刚才弹出的 mid 形成凹槽,还可能和更左边的元素形成更大的凹槽。 所以我们要用 while 循环重复步骤 2 和 3,直到栈顶元素不再小于 height[i]。最后,将当前的 i 入栈,因为它也可能成为未来的"左边界"。
5.后续处理
遍历结束以后,栈中的即使还有元素也不用匹配了,右边界不存在,无法接雨水。
具体代码
cpp
int trap(vector<int>& height) {
if (height.size() <= 2) return 0;
int sum = 0;
stack<int> st; // 单调递减栈,存下标
for(int i = 0; i < height.size(); i++)
{
// 步骤 2 & 4: 当遇到更高的柱子(右边界),循环处理之前的凹槽
while(!st.empty() && height[i] > height[st.top()])
{
// 步骤 2: 获取凹槽底部的下标
int mid = st.top();
st.pop();
// 如果栈空,说明没有左边界,无法接水
if(st.empty()) break;
// 步骤 3: 获取左边界,计算高和宽
int left = st.top();
int h = min(height[left], height[i]) - height[mid];
int w = i - left - 1;
sum += h * w;
}
// 步骤 1 & 4: 保持单调递减,入栈
st.push(i);
}
return sum;
}结语
从寻找无序子数组的边界,到判断回文链表,再到经典的接雨水困难题,我们一步步攻克了数组、链表和栈这三大关卡。
你可能会觉得"接雨水"的单调栈逻辑比较晦涩,这很正常。请试着回过头再去刷一遍"每日温度",弄清楚为什么栈里存的是下标 ,以及什么时候该出栈。当你彻底理解了"每日温度"中寻找"下一个更高值"的逻辑,再看接雨水的"找凹槽"过程,就会有一种豁然开朗的感觉。
每一道 Hard 题,其实都是由若干个 Easy 或 Medium 的知识点拼接而成的。保持耐心,继续刷题,我们下一篇文章见!
以上就是本期博客的全部内容,感谢各位的阅读以及观看。如果内容有误请大佬们多多指教,一定积极改进,加以学习。
