
/-----------初阶数据结构-----------/
【栈和队列面试题目录】:
[一、 栈和队列面试题](#一、 栈和队列面试题)
谁学数据结构没被栈和队列 "折磨" 过?面试要写括号匹配、用栈造队列,选择题还得算循环队列长度、辨出栈序列 ------ 既要敲代码又要抠概念,主打一个 "全方位考察"。这篇直接端上 4 道面试题 + 5 道选择题,解法 + 坑点 + 考点一次性捋顺,主打一个 "练完少踩坑"。
一、 栈和队列面试题
Ⅰ、有效的括号
【题目】:https://leetcode.cn/problems/valid-parentheses/

【思路】:
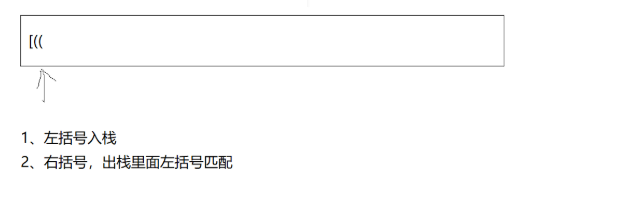
用栈存左括号,遇到右括号就弹出栈顶匹配,不匹配 / 栈空 / 最后栈非空都返回 false,反之合法
【代码】:
cpp
class Solution {
public:
bool isValid(string s) {
stack<char> st;
int i = 0;
while(i < s.size())
{
// 左括号:入栈暂存,等待匹配
if(s[i] == '[' || s[i] == '(' || s[i] == '{')
{
st.push(s[i]);
}
// 右括号:校验匹配性
else
{
// 边界1:只有右括号(栈空无左括号可匹配)
if(st.empty())
{
return false;
}
char top = st.top();
st.pop();
// 核心校验:栈顶左括号与当前右括号类型不匹配
if(top == '(' && s[i] != ')'||top == '[' && s[i] != ']'||top == '{' && s[i] != '}')
{
return false;
}
}
i++;
}
// 边界2:左括号未匹配完(栈非空)
int ret = st.empty();
return ret;
}
};Ⅱ、用队列实现栈
【题目】:https://leetcode.cn/problems/implement-stack-using-queues/

【思路】:

【代码】:
cpp
class MyStack {
public:
MyStack()
{
}
// 核心:新元素始终压入非空队列,保证数据集中在一个队列里(模拟栈的元素存储)
void push(int x) {
if(!q1.empty())
{
q1.push(x);
}
else
{
q2.push(x);
}
}
// 核心:把非空队列的前n-1个元素移到空队列,仅留最后1个(栈顶元素)弹出,模拟栈"后进先出"
int pop() {
// 处理q1非空的情况
if(!q1.empty())
{
// 移走q1中除最后1个外的所有元素到q2
while(q1.size()>1)
{
q2.push(q1.front());
q1.pop();
}
// 取出栈顶元素(q1仅剩的最后一个元素)
int top = q1.front();
q1.pop();
return top;
}
// 处理q2非空的情况(逻辑和q1完全一致)
else
{
while(q2.size()>1)
{
q1.push(q2.front());
q2.pop();
}
int top = q2.front();
q2.pop();
return top;
}
}
// 核心:栈顶元素 = 非空队列的队尾元素(队列内元素顺序和栈一致)
int top() {
if(!q1.empty())
{
return q1.back();
}
else
{
return q2.back();
}
}
// 核心:栈空 = 两个队列都为空(无任何元素残留)
bool empty() {
return q1.empty() && q2.empty();
}
private:
queue<int> q1; // 辅助队列1
queue<int> q2; // 辅助队列2
};
/**
* Your MyStack object will be instantiated and called as such:
* MyStack* obj = new MyStack();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->top();
* bool param_4 = obj->empty();
*/Ⅲ、用栈实现队列
【题目】:https://leetcode.cn/problems/implement-queue-using-stacks/
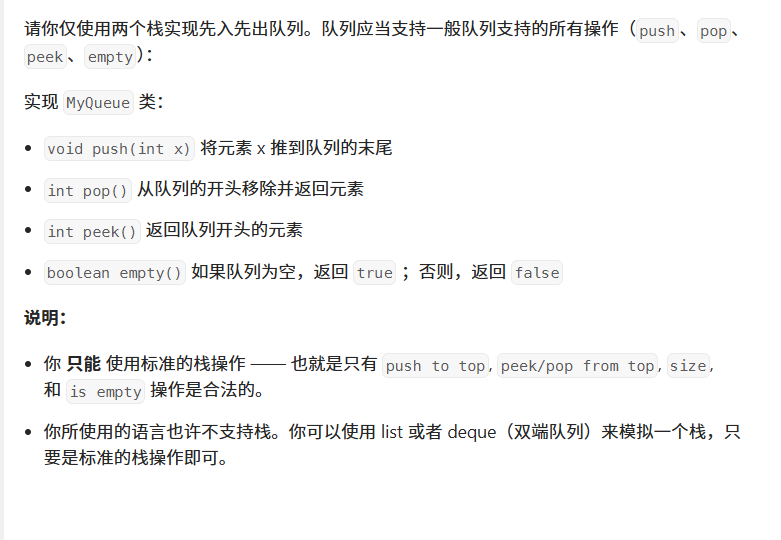
【思路】:
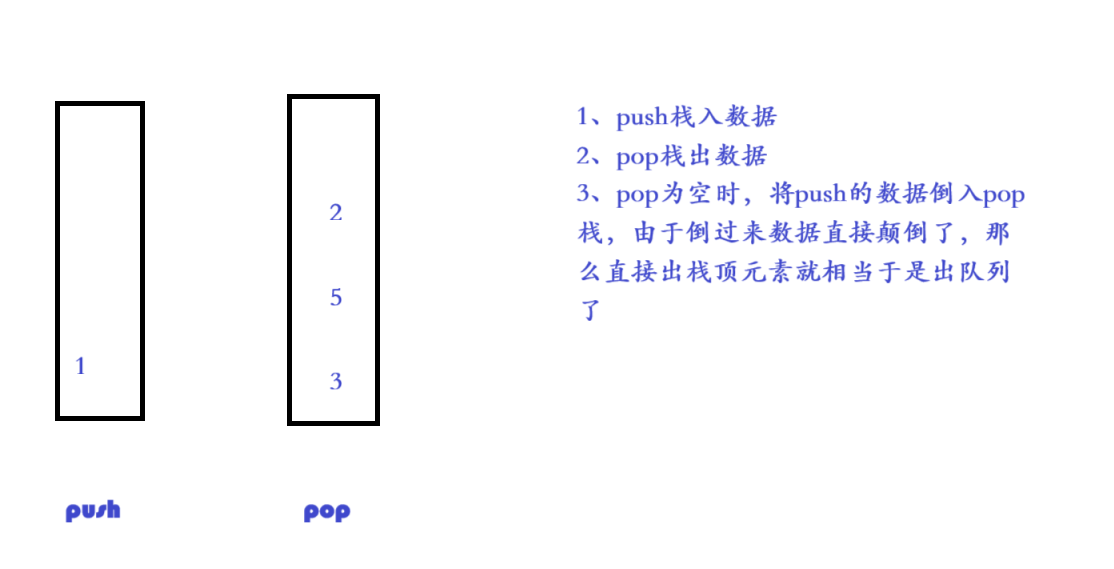
【代码】:
cpp
class MyQueue {
public:
MyQueue() {}
// 核心:入队只往pushst压入元素
void push(int x) {
pushst.push(x);
}
// 核心:popst空则将pushst元素倒过来(反转顺序),取popst栈顶(队头)弹出
int pop() {
if(popst.empty()) {
// pushst元素倒入popst,实现先进先出
while(!pushst.empty()) {
popst.push(pushst.top());
pushst.pop();
}
}
assert(!popst.empty()); // 防御:避免队空时调用pop
int ret = popst.top();
popst.pop();
return ret;
}
// 核心:逻辑同pop,仅取队头不弹出
int peek() {
if(popst.empty()) {
while(!pushst.empty()) {
popst.push(pushst.top());
pushst.pop();
}
}
assert(!popst.empty()); // 防御:避免队空时调用peek
return popst.top();
}
// 核心:队列空 = 两个栈都为空
bool empty() {
return popst.empty() && pushst.empty();
}
private:
stack<int> pushst; // 仅用于入队的栈
stack<int> popst; // 仅用于出队/查队头的栈
};
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue* obj = new MyQueue();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->peek();
* bool param_4 = obj->empty();
*/Ⅳ、设计循环队列
【题目】:https://leetcode.cn/problems/design-circular-queue/

【思路】:
这道题的核心是实现循环队列的完整操作接口,如果你对循环队列的实现细节不太熟悉,可以参考我之前的内容,里面有循环队列的详细实现方案,能帮你快速理清思路~【参考文章】
【代码】:
循环队列的实现方案较为灵活,本次我采用数组的方式来完成具体实现~
cpp
class MyCircularQueue {
public:
// 构造函数:初始化循环队列,分配k大小的数组空间,初始化指针/计数变量
MyCircularQueue(int k) {
a = new int[k]; // 堆区分配数组,容量为k
front = rear = size = 0; // 队头/队尾指针、元素个数初始化为0
capacity = k; // 队列最大容量设为k
}
// 核心:判空 - 元素个数为0则队空
bool isEmpty() {
return size == 0;
}
// 核心:判满 - 元素个数等于容量则队满
bool isFull() {
return size == capacity;
}
// 核心:入队 - 队不满时,将值存入rear位置,rear循环后移,元素个数+1
bool enQueue(int value)
{
if(isFull()) // 队满则入队失败
return false;
a[rear] = value; // 新元素存入当前rear位置
rear = (rear + 1) % capacity; // rear循环后移(取模实现循环)
size++; // 元素个数+1
return true; // 入队成功
}
// 核心:出队 - 队不空时,front循环后移,元素个数-1
bool deQueue()
{
if(isEmpty()) // 队空则出队失败
return false;
front = (front + 1) % capacity; // front循环后移(取模实现循环)
size--; // 元素个数-1
return true; // 出队成功
}
// 核心:取队头 - 队不空时返回front指向的元素
int Front() {
if(isEmpty())
return -1; // 队空返回-1(题目约定)
return a[front];
}
// 核心:取队尾 - 队不空时,根据rear位置分支取队尾元素
int Rear() {
if(isEmpty())
return -1; // 队空返回-1(题目约定)
// rear指向队尾下一个位置:
// 1. rear=0 → 队尾在数组最后一位(capacity-1)
// 2. rear≠0 → 队尾在rear前一位(rear-1)
return rear == 0 ? a[capacity-1] : a[rear-1];
}
private:
int *a; // 数组:存储循环队列元素
int front; // 队头指针:指向队头元素
int rear; // 队尾指针:指向队尾元素的下一个位置
int size; // 当前元素个数:快速判空/判满
int capacity; // 队列最大容量:数组总大小
};
/**
* Your MyCircularQueue object will be instantiated and called as such:
* MyCircularQueue* obj = new MyCircularQueue(k);
* bool param_1 = obj->enQueue(value);
* bool param_2 = obj->deQueue();
* int param_3 = obj->Front();
* int param_4 = obj->Rear();
* bool param_5 = obj->isEmpty();
* bool param_6 = obj->isFull();
*/二、概念选择题

栈是 "后进先出"------ 最后入栈的元素最先出栈。入栈顺序是
1、2、3、4、5、A、B、C、D、E(E 最后入栈),出栈就从 E 开始倒着取,顺序是E、D、C、B、A、5、4、3、2、1,对应选项B。

逐一模拟验证选项:
- A:1 入→1 出;2、3、4 入→4 出、3 出、2 出 → 可行;
- B:1、2 入→2 出;3 入→3 出;4 入→4 出;1 出 → 可行;
- C :要先出 3,需 1、2、3 入→3 出;此时栈内是 1、2(2 在栈顶),但选项接下来出 1------1 在 2 下面,无法跳过 2 先出 1 → 不可行;
- D:1、2、3 入→3 出;4 入→4 出;2 出、1 出 → 可行。

循环队列中,
front=rear对应两种情况:
- 队空:元素数 = 0;
- 队满:元素数 = 容量(本题为 100)。
结论:元素数为 0 或 100,选 D。

队列是 "先进先出" 结构,基本运算只针对队头 / 队尾操作:
- A(队尾插入)、C(判空)、D(读取队头)都是队列基本运算;
- B(删除第 i 个元素)是 "随机访问删除",违背队列 "先进先出" 的操作规则,不是队列基本运算。

步骤 1:画 "未绕圈" 场景
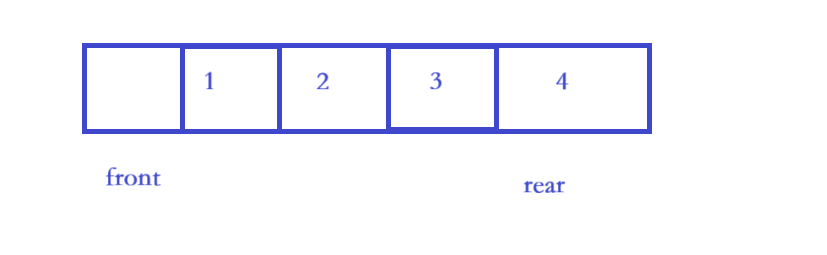
设 N=5,front=0(空),rear=4(有效元素是 1、2、3、4,共 4 个)。
- 代入选项 B:
(4 - 0 + 5) % 5 = 9 % 5 = 4(= 实际元素数 4,对)
步骤 2:画 "绕圈" 场景
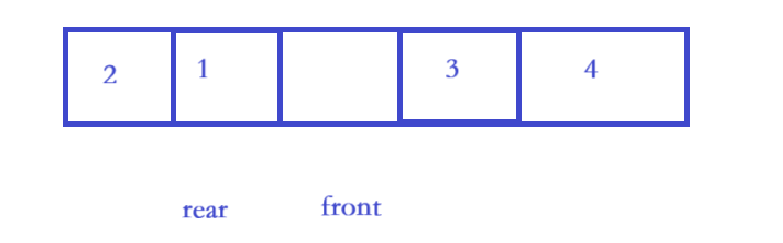
设 N=5,front=2(空),rear=1(有效元素是 2、1、3、4,共 4 个)。
- 代入选项 B:
(1 - 2 + 5) % 5 = 4 % 5 = 4(= 实际元素数 4,对)