27 Anomaly Detection 异常检测
27.1 Finding Unusual Events
最常见的异常检测算法是密度估计,构建一个概率模型,如果 p(xtest)<εp(x_{test})<\varepsilonp(xtest)<ε,标记为异常
27.2 Gaussian (Normal) Distribution
建模p(x)p(x)p(x)需要用到高斯分布(正态分布,钟形分布)
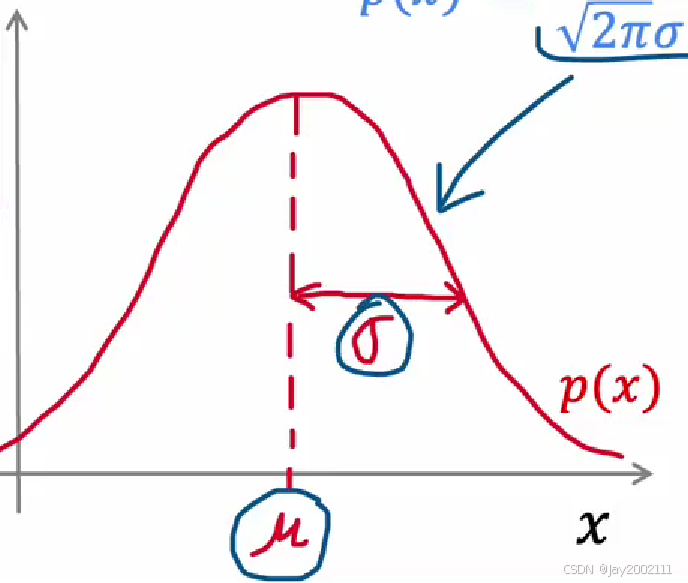
高斯分布概率密度函数:
p(x)=12πσe−(x−μ)22σ2p(x) = \frac 1 {\sqrt{2\pi}\sigma}e^{\frac {-(x - \mu)^2} {2\sigma^2}}p(x)=2π σ1e2σ2−(x−μ)2
概率分布图:
注:
- μ\muμ是均值,控制了中心位置
- σ\sigmaσ是标准差,控制了宽度(分散程度)
- 由于概率密度函数在某一区域上的积分就是这个区域内随机变量取值的概率,即围成的面积(概率之和)为1,如果σ\sigmaσ减小,曲线变窄,曲线的峰值会变高
接下来介绍最大似然估计(Maximum Likelihood Estimation,MLE),核心思想:
假设我们有一个模型(比如高斯分布),但不知道它的参数(比如 μ\muμ 和 σ2\sigma^2σ2)。我们观察到了一组样本数据 D={x1,x2,...,xn}D = \{x_1, x_2, \dots, x_n\}D={x1,x2,...,xn},MLE 认为,我们应该选择一个参数 θ^\hat{\theta}θ^(例如 μ^,σ^2\hat{\mu}, \hat{\sigma}^2μ^,σ^2)使得:在所有可能的参数值中,当前观察到的样本数据出现的概率最大
似然函数(Likelihood Function):对于一个参数集合 θ\thetaθ 和一组独立同分布(Independent and Identically Distributed,i.i.d.)的样本 D={x1,x2,...,xn}D = \{x_1, x_2, \dots, x_n\}D={x1,x2,...,xn},似然函数L(θ)L(\theta)L(θ)定义为观测到这些样本的联合概率:
L(θ)=P(x1,x2,...,xn∣θ)L(\theta) = P(x_1, x_2, \dots, x_n | \theta)L(θ)=P(x1,x2,...,xn∣θ)
由于样本是独立同分布的,联合概率是各个样本概率的乘积:
L(θ)=∏i=1nf(xi∣θ)L(\theta) = \prod_{i=1}^{n} f(x_i | \theta)L(θ)=i=1∏nf(xi∣θ)
其中f(xi∣θ)f(x_i | \theta)f(xi∣θ)是模型的概率密度函数(或概率质量函数)。
注:求解实践中常常用对数似然函数(取ln),因为可以将连乘转化为连加
回到高斯分布,MLE估计高斯分布参数:
μ^MLE=1n∑i=1nxi\hat{\mu}{MLE} = \frac{1}{n} \sum{i=1}^{n} x_iμ^MLE=n1i=1∑nxi
σ^MLE2=1n∑i=1n(xi−μ^MLE)2\hat{\sigma}^2_{MLE} = \frac{1}{n} \sum_{i=1}^{n} (x_i - \hat{\mu}_{MLE})^2σ^MLE2=n1i=1∑n(xi−μ^MLE)2
回到密度估计(异常检测),估计出样本的概率密度函数,然后看样本值xtestx_{test}xtest对应的p(xtest)p(x_{test})p(xtest)的值是否小于极小值ε\varepsilonε即可,小于的话标为异常值
但目前讨论的是单特征密度估计的情况,接下来讨论可以处理多个特征的更复杂的异常检测算法
27.3 Anomaly Detection Algorithm
基本假设:各个特征之间时统计独立的,但是事实证明大多数情况下,即使特征之间不是统计独立的,该算法也能表现良好
记我们现在有特征向量x⃗\vec xx ,那么其概率:
p(x)=∏j=1np(xj;μj,σj2)p(x) = \prod_{j=1}^n p(x_j; \mu_j, \sigma_j^2)p(x)=j=1∏np(xj;μj,σj2)
总结一下流程:
- 选择n个特征
- 最大似然估计,算出n个特征各自的参数μ\muμ 和 σ2\sigma^2σ2
- 代入p(x)p(x)p(x)公式,连乘,比较其值是否小于极小值ε\varepsilonε,是的话标记异常
p(x)=∏j=1np(xj;μj,σj2)=∏j=1n12πσje−(x−μj)22σj2p(x) = \prod_{j=1}^n p(x_j; \mu_j, \sigma_j^2) = \prod_{j=1}^n \frac 1 {\sqrt{2\pi}\sigma_j}e^{\frac {-(x - \mu_j)^2} {2\sigma_j^2}}p(x)=j=1∏np(xj;μj,σj2)=j=1∏n2π σj1e2σj2−(x−μj)2
27.4 Developing and Evaluating an Anomaly Detection System
在实际开发中,需要面临一些决策,例如特征如何选择 和ε\varepsilonε如何选择
很有必要设计一种评估学习算法,可以在改变特征/超参数后计算一个数字,量化表明算法是变好了还是变差了,这种算法被称为**"实数评估"(Real-Valued Evaluation)**:
在异常检测算法里,即使是无监督学习,数据是无标签的,但是我们通常也可以找出部分已知的异常样本,而其他样本可以当做都是正常样本(实际上即使少量异常样本被误认为是正常样本,通常也不影响算法效果)
参考监督学习的方式,构建训练集、测试集、交叉验证集
注:
- 训练集样本认为都是正常的,而测试集和交叉验证集中既有正常也有异常(正常占大多数,异常占极少数)
- 仍然是无监督学习,因为训练样本仍然是无标签的
类似地,调整特征或ε\varepsilonε,观察在交叉验证集上的效果,选取最好的,再在测试集上测试
注:
- 如果异常样本非常少,可以考虑全部放入交叉验证集并移除测试集,但这样容易导致过拟合
- 在交叉验证集的效果观察,通常是统计混淆矩阵(即真阳,真阴,假阳,假阴),然后计算准确率和召回率(或者F1F_1F1分数)来评判
27.5 Anomaly Detection vs. Supervised Learning
如果我们有已经的有标签的异常数据样本,可以考虑用有监督学习,接下来介绍如何选择
一句话总结:选择哪种方法,取决于我们对"异常"是否拥有先验知识 和足够的标注数据
当我们面对的异常类型是未知且稀有 的,或者我们根本无法获得足够的异常样本标签 时,推荐采用无监督方法。这种方法的核心思想是只关注正常数据的特性。这种方法擅长发现全新、未曾见过的异常模式
如果异常的类型是明确且稳定 的,并且我们有足够的 、高质量的已标记正常和异常样本,那么问题就退化成一个标准的二分类任务。这种方法在已知异常类型上的性能往往更高 ,但弱点在于对训练集中未出现过的新型异常缺乏识别能力
两者并不是不可融合的,例如用监督学习去检测已知的已有大量异常样本的异常,例如检测某个零件生产的常发异常,再用无监督的方式去检测可能偶发的新的异常类型
27.6 Choosing What Features to Use
监督学习可以通过调整特征的权重,弱化不重要的特征,所以即使特征选择错误,影响也不会那么大
但是无监督学习无法通过有标签的数据来识别哪些特征是可以忽略的,所以特征的选择对于无监督学习异常检测来说比有监督学习更重要
主要有两种思路:
- 检查特征的分布是否符合正态分布
通过画直方图,粗略估计特征是否符合正态分布
如果不符合,可以手动尝试对特征进行一些调整,直到特征的直方图看起来基本符合正态分布
例如:加常数取对数log(x+c)log(x+c)log(x+c),或者取若干次方xax^{a}xa等等 - 错因分析
检查交叉验证集中没有被正确识别出的异常样本,尝试找出新特征
新特征可以是旧特征组合而来的,例如检查计算机运行的异常状态,有CPU占用率、内存占用率等特征,发现异常案例是CPU占用率很低并且内存占用率很高时出现异常,可以考虑用两者比值作为新特征