A星融合DWA路径规划算法：静态与动态避障的完美结合

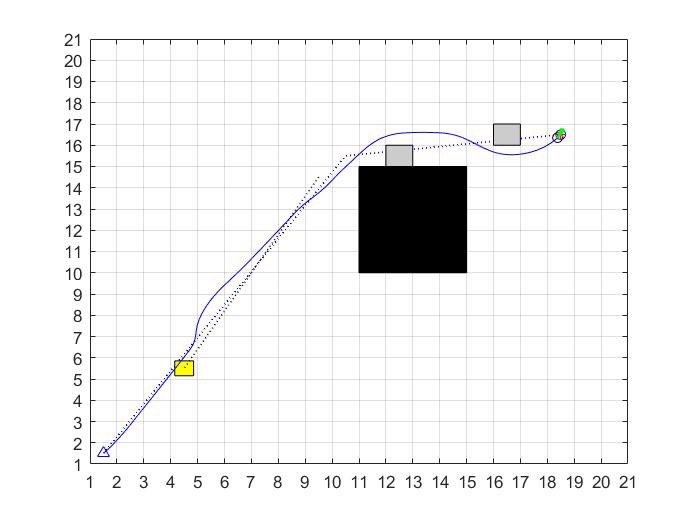
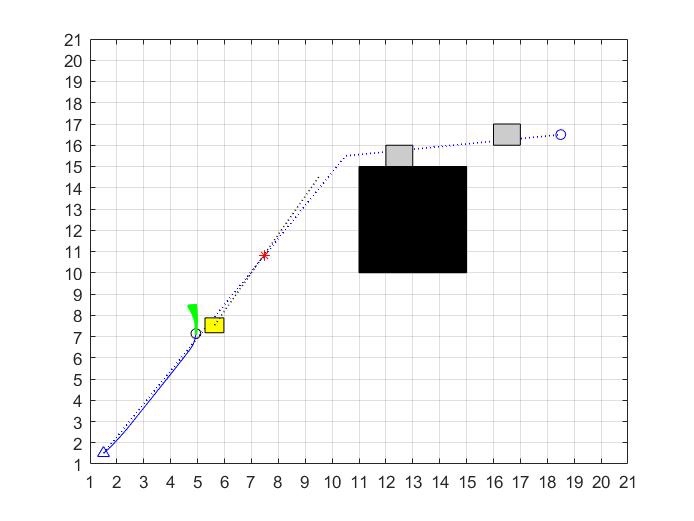
A星融合DWA的路径规划算法，可实现静态避障碍及动态避障,代码注释详细,matlab源码

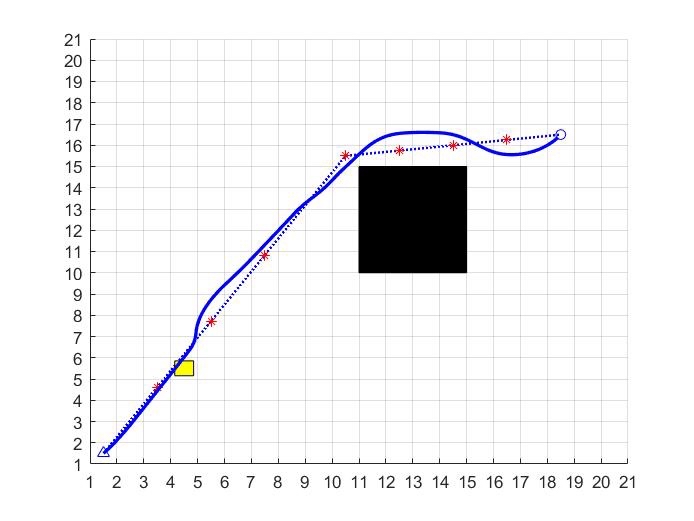
在机器人路径规划领域，A星算法和DWA（Dynamic Window Approach）算法都是非常经典且常用的算法。今天咱们就来聊聊将A星算法和DWA算法融合在一起，实现既能静态避障又能动态避障的路径规划，并且附上详细注释的Matlab源码。

A星算法与DWA算法简介

A星算法

A星算法是一种启发式搜索算法，它通过计算每个节点的代价函数 f(n) = g(n) + h(n) 来寻找最优路径。其中 g(n) 是从起点到节点 n 的实际代价，h(n) 是从节点 n 到目标点的估计代价。简单理解就是，它会综合考虑已经走过的路程和到目标点预估的路程，选择代价最小的路径。

DWA算法

DWA算法主要用于动态环境下的路径规划。它基于机器人当前的速度和加速度限制，在一定的时间窗口内生成一系列可能的轨迹，然后根据与障碍物的距离、接近目标点的程度等评价函数，选择最优的轨迹。

A星融合DWA实现路径规划

这种融合算法的基本思路是，先用A星算法在静态地图上规划出一条大致的全局路径，然后DWA算法根据机器人实时的位置和动态环境信息，在A星规划出的全局路径基础上进行局部调整，实现动态避障。

Matlab源码及详细注释

% 定义地图参数
map_size = [100, 100]; % 地图大小，100x100的网格
obstacle_map = zeros(map_size); % 初始化障碍物地图
% 设置障碍物位置
obstacle_map(20:30, 20:30) = 1; 
obstacle_map(50:60, 50:60) = 1; 

% A星算法部分
start = [1, 1]; % 起点
goal = [map_size(1), map_size(2)]; % 终点
% 计算A星路径
[a_star_path, ~] = a_star(obstacle_map, start, goal);

% DWA算法部分
% 机器人参数
robot_radius = 5; % 机器人半径
max_linear_vel = 1; % 最大线速度
max_angular_vel = pi/4; % 最大角速度
time_step = 0.1; % 时间步长
prediction_time = 1; % 预测时间

% 模拟动态障碍物
dynamic_obstacles = {[30, 40; 31, 40; 32, 40]}; % 动态障碍物位置序列

current_position = start;
dwa_path = [];
for i = 1:length(a_star_path) - 1
    % 获取当前局部目标点
    local_goal = a_star_path(i + 1, :);
    while norm(current_position - local_goal) > 1
        % 执行DWA算法
        [new_vel, ~] = dwa(current_position, local_goal, dynamic_obstacles{i},...
            robot_radius, max_linear_vel, max_angular_vel, time_step, prediction_time, obstacle_map);
        % 更新当前位置
        current_position = current_position + [new_vel(1) * cos(new_vel(2)), new_vel(1) * sin(new_vel(2))] * time_step;
        dwa_path = [dwa_path; current_position];
    end
end

% A星算法函数实现
function [path, cost] = a_star(obstacle_map, start, goal)
    % 初始化
    open_set = [];
    closed_set = [];
    came_from = [];
    g_score = Inf(size(obstacle_map));
    f_score = Inf(size(obstacle_map));
    g_score(start(1), start(2)) = 0;
    f_score(start(1), start(2)) = heuristic(start, goal);
    open_set = [open_set; start];

    while ~isempty(open_set)
        % 找到f_score最小的节点
        [~, min_index] = min(f_score(sub2ind(size(obstacle_map), open_set(:, 1), open_set(:, 2))));
        current = open_set(min_index, :);
        if all(current == goal)
            % 找到路径，回溯
            path = reconstruct_path(came_from, current);
            cost = g_score(goal(1), goal(2));
            return;
        end
        open_set(min_index, :) = [];
        closed_set = [closed_set; current];
        % 遍历邻居节点
        for dx = -1:1
            for dy = -1:1
                if dx == 0 && dy == 0
                    continue;
                end
                neighbor = current + [dx, dy];
                if neighbor(1) < 1 || neighbor(1) > size(obstacle_map, 1) || neighbor(2) < 1 || neighbor(2) > size(obstacle_map, 2) || obstacle_map(neighbor(1), neighbor(2)) == 1
                    continue;
                end
                tentative_g_score = g_score(current(1), current(2)) + 1;
                if ~ismember(neighbor, closed_set, 'rows') && (isempty(find(ismember(open_set, neighbor, 'rows'), 1)) || tentative_g_score < g_score(neighbor(1), neighbor(2)))
                    came_from = [came_from; current; neighbor];
                    g_score(neighbor(1), neighbor(2)) = tentative_g_score;
                    f_score(neighbor(1), neighbor(2)) = tentative_g_score + heuristic(neighbor, goal);
                    if isempty(find(ismember(open_set, neighbor, 'rows'), 1))
                        open_set = [open_set; neighbor];
                    end
                end
            end
        end
    end
    path = [];
    cost = Inf;
end

% 启发式函数
function h = heuristic(node, goal)
    h = norm(node - goal);
end

% 回溯路径函数
function path = reconstruct_path(came_from, current)
    path = [current];
    while ~isempty(came_from) && ~all(came_from(end - 1, :) == current)
        current = came_from(end - 1, :);
        path = [current; path];
        came_from(end - 2:end, :) = [];
    end
end

% DWA算法函数实现
function [best_vel, best_trajectory] = dwa(current_position, local_goal, dynamic_obstacle, robot_radius, max_linear_vel, max_angular_vel, time_step, prediction_time, obstacle_map)
    % 生成速度样本
    linear_vels = linspace(0, max_linear_vel, 10);
    angular_vels = linspace(-max_angular_vel, max_angular_vel, 10);
    best_score = -Inf;
    best_vel = [];
    best_trajectory = [];

    for i = 1:length(linear_vels)
        for j = 1:length(angular_vels)
            vel = [linear_vels(i), angular_vels(j)];
            % 预测轨迹
            trajectory = predict_trajectory(current_position, vel, time_step, prediction_time);
            % 评价轨迹
            score = evaluate_trajectory(trajectory, local_goal, dynamic_obstacle, robot_radius, obstacle_map);
            if score > best_score
                best_score = score;
                best_vel = vel;
                best_trajectory = trajectory;
            end
        end
    end
end

% 预测轨迹函数
function trajectory = predict_trajectory(current_position, vel, time_step, prediction_time)
    num_steps = floor(prediction_time / time_step);
    trajectory = zeros(num_steps, 2);
    for i = 1:num_steps
        current_position = current_position + [vel(1) * cos(vel(2)), vel(1) * sin(vel(2))] * time_step;
        trajectory(i, :) = current_position;
    end
end

% 评价轨迹函数
function score = evaluate_trajectory(trajectory, local_goal, dynamic_obstacle, robot_radius, obstacle_map)
    distance_to_goal = norm(trajectory(end, :) - local_goal);
    % 计算与动态障碍物的距离
    distance_to_dynamic_obstacle = Inf;
    for i = 1:size(dynamic_obstacle, 1)
        for j = 1:size(trajectory, 1)
            dist = norm(trajectory(j, :) - dynamic_obstacle(i, :));
            if dist < distance_to_dynamic_obstacle
                distance_to_dynamic_obstacle = dist;
            end
        end
    end
    % 计算与静态障碍物的距离
    distance_to_static_obstacle = Inf;
    for i = 1:size(trajectory, 1)
        x = round(trajectory(i, 1));
        y = round(trajectory(i, 2));
        if x >= 1 && x <= size(obstacle_map, 1) && y >= 1 && y <= size(obstacle_map, 2) && obstacle_map(x, y) == 1
            distance_to_static_obstacle = 0;
            break;
        end
    end
    % 综合评价
    score = 1 / distance_to_goal + 1 / (distance_to_dynamic_obstacle + 1) + 1 / (distance_to_static_obstacle + 1);
end

这段代码首先定义了地图和障碍物信息，然后通过A星算法规划出全局路径，接着在A星路径的基础上，利用DWA算法结合动态障碍物信息进行局部路径调整。在代码实现中，每个函数都有明确的功能和详细注释，方便大家理解。

总结

A星融合DWA的路径规划算法结合了两者的优势，在静态环境中可以高效地找到全局最优路径，在动态环境下又能灵活地避开动态障碍物。希望这篇博文和代码示例能帮助大家更好地理解和应用这种算法。如果有任何问题，欢迎在评论区留言交流。