OpenCV(三十七)：外接矩形

三类常见定义

OpenCV 中主要有三种常用外接矩形：

1. axis-aligned bounding box（AABB 轴对齐最小外接矩形）

使用 cv2.boundingRect(contour)

特点：

矩形边始终与 X、Y 轴平行
覆盖轮廓的最小面积矩形（在轴对齐限制下）
简单、速度快
不考虑旋转角度，因此对倾斜目标可能较大

数学原理：

对轮廓得到所有点的 xmin、xmax、ymin、ymax：

ini 复制代码

w = xmax - xmin
h = ymax - ymin

2. minimum area bounding rectangle（旋转最小外接矩形）

使用 cv2.minAreaRect(contour)

该矩形是面积最小的外接矩形，允许旋转。

特点：

能贴合物体方向
利用点集求凸包 + Rotating Calipers（旋转卡尺算法）
输出中心点、尺寸、旋转角度

矩形可更精确描述 非水平物体（如倾斜条码、车牌、笔、手机等）。

数学原理（简述）：

对轮廓做凸包
对凸包依次旋转，使某条边与 x 轴平行
在每个旋转角度下计算外接矩形面积
取面积最小者

关键：这是一个 几何最优化问题，时间复杂度接近线性 O(n)。

3. 最小包围圆/椭圆

常见为：

cv2.minEnclosingCircle(contour)
cv2.fitEllipse(contour)

虽然不是矩形，但常与外接矩形一起使用，用于形状更规则的物体。

适用场景：球体、圆盘、胶囊型物体。

适用场景比较

方法	精度	是否旋转	速度	适用场景
`boundingRect`	中等	否	最快	ROI 裁剪、初步定位、跟踪初始化
`minAreaRect`	高	是	较快	倾斜目标，真实物体方向分析，条码/车牌检测
`fitEllipse`	针对椭圆	是	较慢	圆形、椭圆形物体分析

示例

三种外接矩形

python 复制代码

import cv2
import numpy as np

# 读取图像
img = cv2.imread("test.jpg")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 二值化
_, binary = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)

# 获取轮廓
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

for cnt in contours:
    # ====== 1. 轴对齐外接矩形 ======
    x, y, w, h = cv2.boundingRect(cnt)
    cv2.rectangle(img, (x, y), (x+w, y+h), (0, 255, 0), 2)

    # ====== 2. 旋转最小外接矩形 ======
    rect = cv2.minAreaRect(cnt)   # 返回 (中心点, (宽度,高度), 旋转角度)
    box = cv2.boxPoints(rect)
    box = np.int0(box)
    cv2.drawContours(img, [box], 0, (0, 0, 255), 2)

    # ====== 3. 最小外接圆 ======
    (cx, cy), radius = cv2.minEnclosingCircle(cnt)
    cv2.circle(img, (int(cx), int(cy)), int(radius), (255, 0, 0), 2)

cv2.imshow("result", img)
cv2.waitKey(0)
cv2.destroyAllWindows()

执行效果：

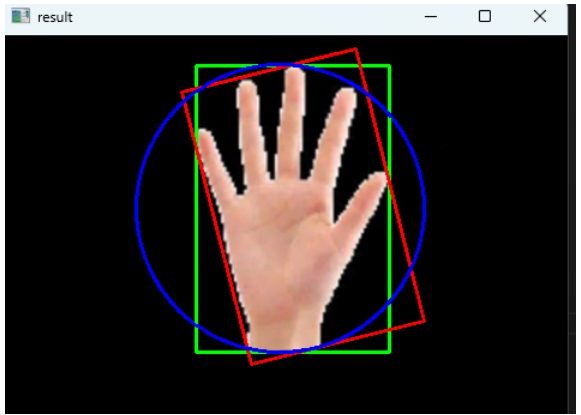
总结

boundingRect 快速、简单，但不考虑旋转
minAreaRect 使用旋转卡尺得到真正意义上的最小外接矩形，是多数精确几何问题首选
选择方法需根据对象形状和业务场景决定
旋转矩形角度处理要特别注意
通过透视变换可获得真实旋转区域的裁剪图像