目录
[1.1 全连接神经网络的结构](#1.1 全连接神经网络的结构)
[Sigmoid 函数](#Sigmoid 函数)
[1.2 全连接神经网络的训练过程](#1.2 全连接神经网络的训练过程)
[1.2.1 前向传播](#1.2.1 前向传播)
[1.2.2 损失函数](#1.2.2 损失函数)
[1.2.3 反向传播](#1.2.3 反向传播)
[2.1 卷积](#2.1 卷积)
[2.1.1 卷积运算](#2.1.1 卷积运算)
[2.1.2 步幅与填充](#2.1.2 步幅与填充)
[2.1.3 多通道卷积](#2.1.3 多通道卷积)
[2.2 池化操作](#2.2 池化操作)
[2.3 CNN反向传播](#2.3 CNN反向传播)
[2.4 总结](#2.4 总结)
一、全连接神经网络
在深度学习中，全连接神经网络是最基础、最具代表性的模型结构之一。
1.1 全连接神经网络的结构
从结构上看，全连接神经网络由输入层、若干隐藏层以及输出层组成。输入层 用于接收原始特征向量；隐藏层 负责对输入特征进行逐层非线性变换；输出层则输出最终的预测结果。
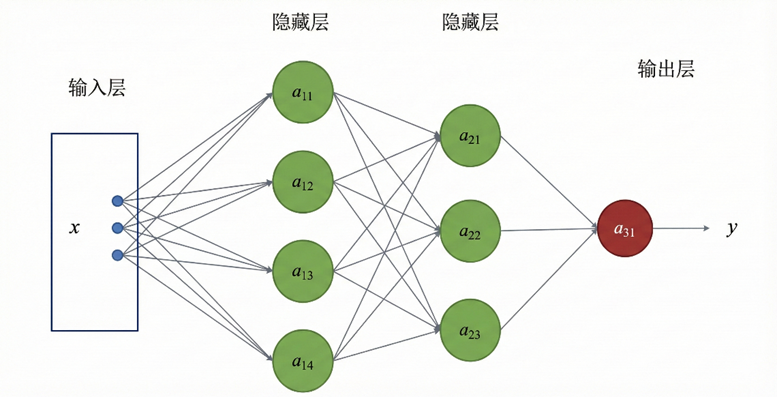
在隐藏层中，相邻两层之间采用全连接方式：上一层的每一个神经元都会与下一层的所有神经元相连。每一层本质上由若干神经元组成，而每个神经元都执行相同的计算流程。其前向计算过程通常可表示为
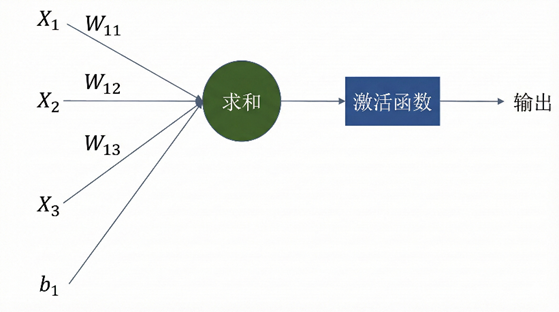
x 表示来自上一层的输入向量，w、b为参数，函数 h() 则称为激活函数。对线性结果进行非线性映射，使神经网络能够逼近复杂的非线性函数；若缺少激活函数，多层网络在表达能力上将退化为单一的线性模型。
常见的激活函数包括以下几类：
Sigmoid 函数
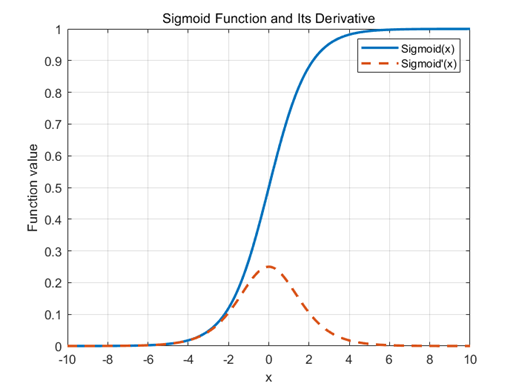
梯度消失：当输入 x 的绝对值较大时，函数输出趋于1，其导数接近于0，反向传播过程中梯度逐层衰减，深层网络难以有效训练。
输出区间关于0不对称
Tanh （双曲正切）函数
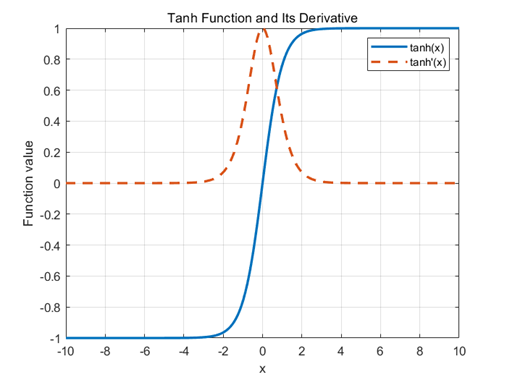
关于0对称，参数更新时不易产生系统性偏移，收敛速度更快
输入绝对值较大时同样会梯度消失
ReLU 函数
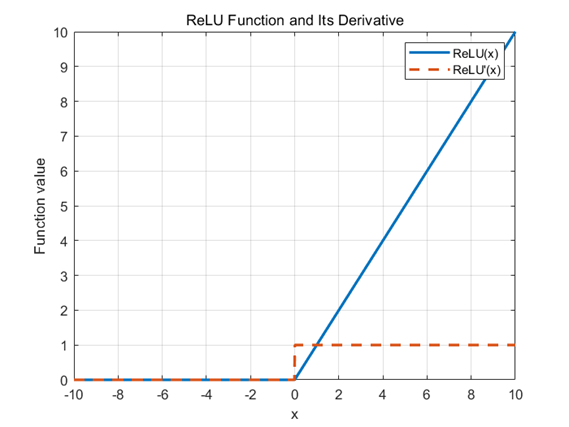
在正区间内具有恒定梯度，缓解了深层网络的梯度消失问题。计算形式简单
某些神经元在训练过程中长期接收到负输入，其输出恒为零，梯度也始终为零，无法继续更新，神经元死亡。
Leaky ReLU
𝛼是一个取值较小的正数，通常设为 0.01或0.02
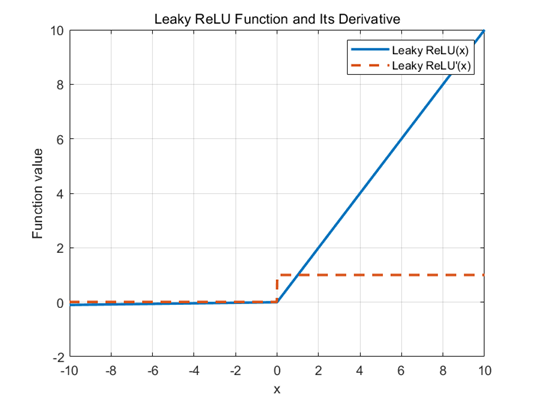
负区间保持非零梯度，避免神经元死亡
缺乏统一的最优选择标准
1.2 全连接神经网络的训练过程
全连接神经网络的训练本质上是一个参数优化问题。模型通过不断调整网络中各层的权重w和偏置参数b，使输出逼近真实标签。训练过程由前向传播、损失计算和反向传播构成。
1.2.1 前向传播
输入数据从输入层开始，逐层经过线性变换与非线性激活函数，最终在输出层产生预测结果。设第 𝑙层的输入为 ，其权重矩阵和偏置向量分别为
和
，该层的计算过程可表示为：
对每一层而言，前一层的输出是后一层的输入。通过层层映射，网络逐步将原始输入变换为更高层次的抽象表示，最终在输出层得到模型预测值
1.2.2 损失函数
为了衡量预测结果与真实标签之间的差异，引入损失函数对预测误差定量描述。训练的目标是最小化该损失。
对于回归任务，常用的损失函数包括均方误差, 表示模型输出值（预测值），y表示标签值
对于分类任务，常采用交叉熵损失，如二分：
1.2.3 反向传播
我们的目的是使用输出误差优化网络参数 ，得到损失函数之后，从输出层开始，将误差信号逐层向输入方向传递，根据这个误差优化每一层参数，具体实现方法是梯度下降法
损失函数是w和b 的函数，我们的目标是调整w和b使损失函数最小 。首先针对w分析，将b看作常数，此时损失函数是关于w的函数，下降最快 的方向是负梯度方向
更新规则为：
同理，对于b：
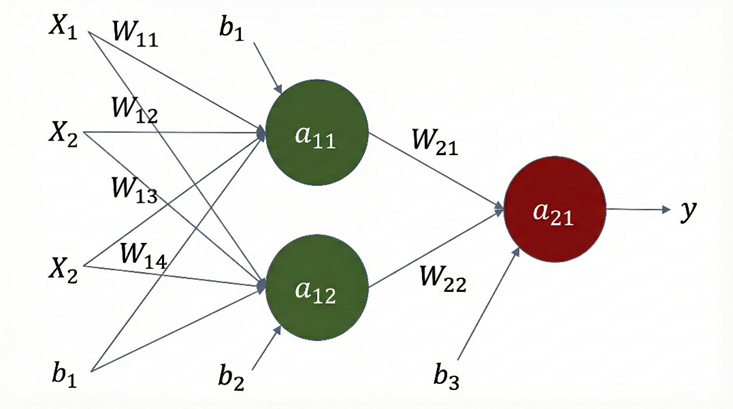
学习率 𝜂表示更新步长，梯度通过链导法则计算,如对下图所示网络：
...
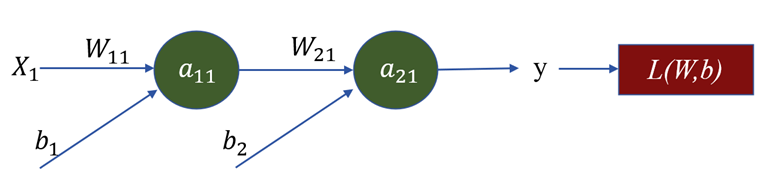
其他参数同理。这样完成了一轮次的参数的更新
模型训练过程中，前向传播、计算误差、反向传播这三个步骤被反复执行，直至模型收敛或达到预设的训练轮数。
总的来说，神经网络的过程需要1.搭建网络结构；2.把数据输入到网络中，3.模型训练，包括前向传播、计算误差、反向传播；4.重复达到训练轮次，得到训练好的模型；5.最后进行测试和使用。
二、卷积神经网络
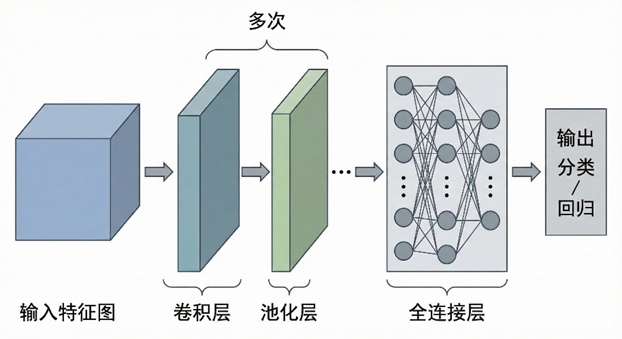
在图像处理任务中，直接使用全连接神经网络需要将图像展开为一维向量。如此会打乱原有的图像结构，同时带来极其庞大的参数数量，不仅计算开销大，也容易过拟合。我们需要一种能够保留空间信息、建模局部特征的网络结构，这便引出了卷积神经网络。
2.1 卷积
2.1.1 卷积运算
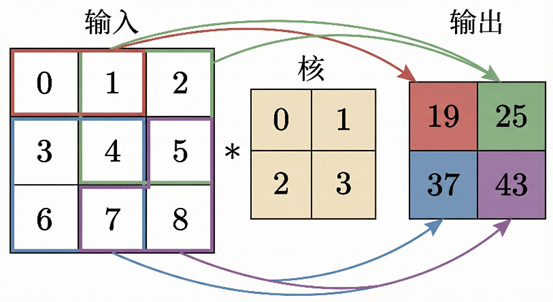
与全连接层不同，卷积层的输入不再是一维向量，而是二维或三维的特征图。卷积核可以理解为一组可学习的权重 𝑤，它以矩阵的形式存在，例如 1*1、3*3、5*5等。
一个卷积核不与整个输入特征图运算，而是从左上角开始，在输入特征图上按一定顺序滑动，与当前位置的局部区域进行内积运算，从而得到输出特征图中的一个像素值。
通过这种方式，卷积操作能够提取图像的局部特征。卷积核在整张特征图上滑动完成后，形成一张输出特征图。
卷积层同样包含偏置项 𝑏。输入特征图与卷积核进行卷积运算后，加上偏置，再通过激活函数，得到最终的输出特征图。
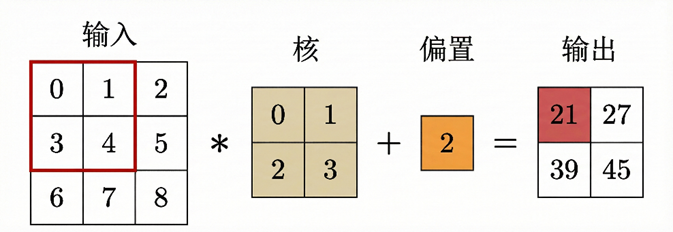
与全连接层相比，区别在于卷积核的大小与数量是人为确定的，可以是2*2，也可以是1*1、3*3，每一个卷积核都会生成一张对应的输出特征图，从而在同一层中提取多种不同类型的特征。
2.1.2 步幅与填充
步幅与填充均可用于控制输出特征图的大小
在卷积运算中，卷积核每次在特征图上移动的步长称为步幅。步幅越大，卷积核移动得越快，输出特征图的尺寸也会相应减小。
随着多次卷积操作，特征图的尺寸会不断变小。为了解决这一问题，通常会在输入特征图的边缘进行填充（Padding），即在四周补零或补其他数值，控制输出特征图的尺寸。
卷积运算后输出特征图的大小可由以下公式计算：
其中，𝑁表示输入特征图尺寸，𝐹为卷积核尺寸，𝑃为填充大小，𝑆为步幅。当计算结果出现小数时，通常向下取整。
2.1.3 多通道卷积
在实际图像中常见的是彩色图像。彩色图像通常由多个通道组成，例如 RGB 图像包含红、绿、蓝三个通道。此时，输入特征图不再是二维的，而是三维的。比如宽、高为128的特征图表示为（128*128*3）
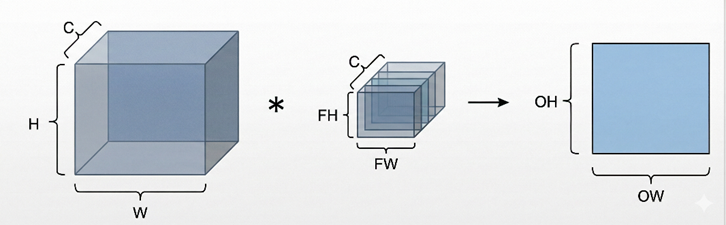
在多通道卷积中，卷积核的深度与输入通道数相同。卷积运算时，卷积核会分别与每一个通道对应位置进行卷积计算，然后将所有通道上的结果相加 ，得到一个输出值。对应输出特征图中的一个像素点。与单通道卷积相比只是多了求和的过程
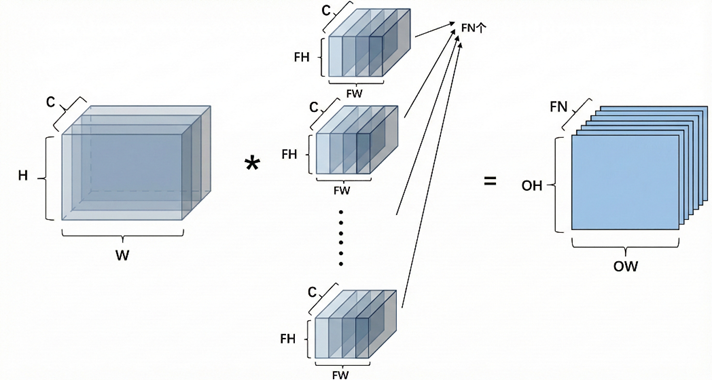
这样的计算得到的是一个卷积核的输出特征图，当设置多个卷积核时，就会得到多张输出特征图，所有这些特征图组合在一起，构成下一层的输入。这里特征图的个数就是下一层输入的通道数
2.2 池化操作
卷积神经网络中，除了卷积操作外，常常还会使用池化（Pooling）操作对特征图下采样。池化减小了特征图尺寸。
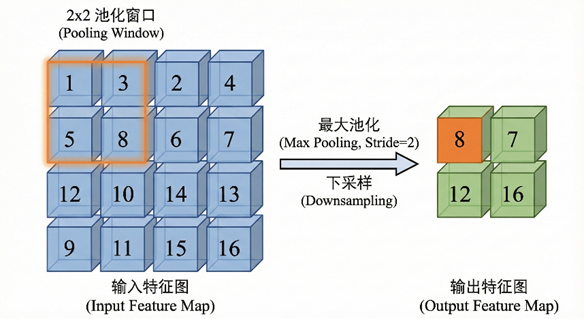
常见的池化方式包括最大池化和平均池化。最大池化是在局部区域内取最大值作为输出，而平均池化则取该区域内的平均值。池化后特征图尺寸为：
H, W 为输入特征图的高度和宽度、 为池化窗口（或卷积核）的高度和宽度、P为填充大小、S为步幅
严格来说，池化不包含可学习参数，并不是神经网络中的一层。只是一种操作，对特征图进行压缩。池化并不是CNN不可或缺的组成部分，事实上，许多模型选择用可学习的下采样方式来替代它。
2.3 CNN反向传播
经过多轮卷积池化操作，输出的多维特征图展平为一维向量输入全连接层。得到模型预测值和损失函数
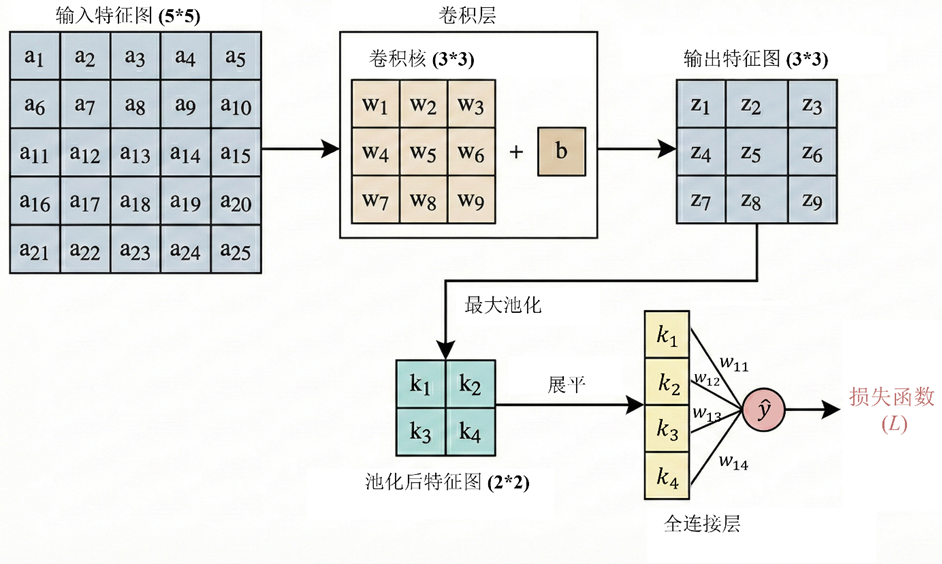
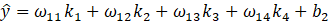
与全连接网络相似，卷积核中的权重 𝑤 以及偏置 𝑏同样通过反向传播和梯度下降法进行更新。核心是求出损失函数对他们的偏导
设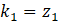
、
、
、
，
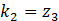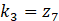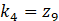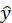是的多元函数
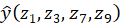，且z1为w1-w9、b的多元函数，由多变量链式法则
可知：
之后经梯度下降参数更新：
...
与全连接网络相似，模型训练过程中前向传播、计算误差、反向传播这三个步骤被反复执行，直至模型收敛或达到预设的训练轮数。
2.4 总结
我们所看到的特征图 ，即卷积层的输出通常是一个二维矩阵。它有宽高，可以可视化成灰度图或热力图，像是一张新的图像。但这只是形式相似，含义完全不同。如果说一个卷积核对应一种特征 ，特征图表示某个卷积核的激活强度分布 ，即某个卷积核对应特征的强弱分布 。比如一个竖直边缘卷积核，在竖直边缘处响应强，而在平坦区域响应弱。
不同卷积核对应不同特征。在靠近输入的卷积层，它们的输入通道是RGB或原始像素，得到的浅层 特征图感知低级结构，如水平/垂直边缘、角点、简单的亮暗变化等；中间层 以各种边缘、角点、纹理特征作为输入，通过在通道维度上组合特征，学习到形状、结构等特征；而输入结构级特征的深层特征图走向抽象和语义，如人的眼睛、车的轮子、字符等特征。由浅入深的，CNN逐层构建对世界的抽象描述。
总结来说，卷积神经网络通常以特征图 作为输入，经过多次卷积层与池化层 的组合逐步提取特征，再通过全连接层对提取到的特征进行综合，输出最终的分类或回归结果。
