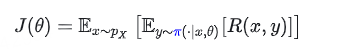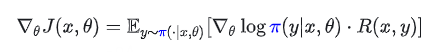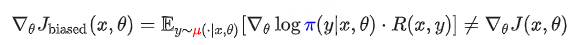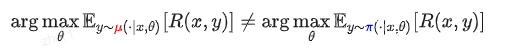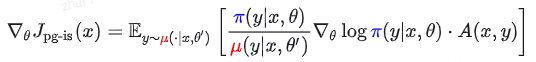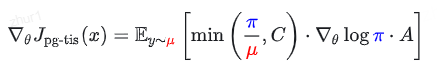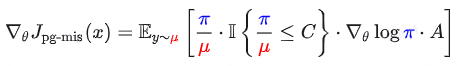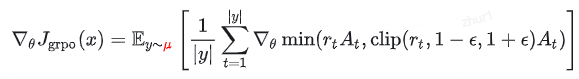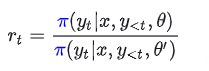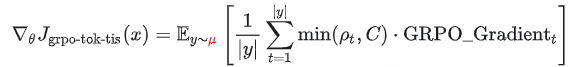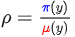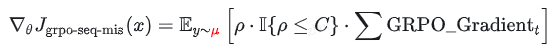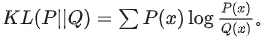为了解决训练不稳定和难以收敛的问题,
业界提出了各种复杂的算法补丁(如Token-level Importance Sampling等)。
但一篇来自Sea AI Lab和新加坡国立大学的最新论文《Defeating the Training-Inference Mismatch via FP16》提出了一个令人震惊的简单结论:
- 我们不需要复杂的算法修正,只需要把精度从 BF16 切回 FP16,一切问题迎刃而解。
一、训练-推理不匹配
1.1 问题的根源:两个引擎的数值差异
在RL 框架中,为了效率,使用了两个不同的策略及其对应的引擎:
推理策略 (Inference Policy) μ( | θ): 使用高度优化的推理引擎(如 vLLM)进行采样。
训练策略 (Training Policy) π( | θ): 使用训练引擎(如PyTorch/DeepSpeed)计算梯度。
虽然理论上 μ = π,但由于数值精度和硬件优化差异,实际上它们并不相等。这产生了两个主要问题:问题一:梯度偏差 (Biased Gradient)
我们希望优化的目标函数是基于训练策略 π 的期望收益:
其中 x 是提示词,y 是回复,R 是奖励。
标准的策略梯度(REINFORCE)应该是:
然而,在实际操作中,样本 y 是从推理策略 μ 中采样出来的。如果我们忽略这种不匹配,直接计算梯度,就会得到一个有偏梯度 (Biased Gradient):
后果: 优化方向发生偏移,导致训练不稳定或崩溃。问题二:部署差距 (Deployment Gap)
即使我们能修正梯度,还有一个无法回避的问题:我们是在优化参数
θ 以适应训练引擎 π,但最终部署时使用的是推理引擎 μ 。
后果: 训练好的模型在实际上线使用时,性能会下降。
1.2 现有的算法修正:重要性采样 (Importance Sampling)
为了修正上述的梯度偏差,学术界引入了重要性采样(IS)。
标准的重要性采样 (IS),通过引入重要性权重 π / μ 来校正分布差异,使梯度重新变得无偏:
其中 A(x, y) 是优势函数。
缺点: 对于长文本,重要性权重方差极大,训练极不稳定。
为了降低方差,研究者提出了两种牺牲少量偏差换取稳定性的变体:
- 截断重要性采样 (Truncated IS, TIS): 设置上限 C
- 掩码重要性采样 (Masked IS, MIS): 如果权重过大直接丢弃
1.3 基于 GRPO 的现有实现及其缺陷
目前的框架大多基于 GRPO 算法。标准的 GRPO 并没有考虑这种不匹配:
标准 GRPO 梯度:
其中:
这里的 rt 是 PPO 中的新旧策略比率,与 μ 无关。
为了解决不匹配,近期工作(如 Yao et al. 和 Liu et al.)给 GRPO 打了补丁:
Token 级 TIS 修正 (GRPO-Tok-TIS): 引入
进行加权:
序列级 MIS 修正 (GRPO-Seq-MIS): 使用整个序列的概率比
进行掩码过滤:
虽然这些公式在数学上试图修正偏差,但它们导致了巨大的计算开销。额外开销: 为了计算上面的 ρ 或 ρt,模型需要额外进行一次前向传播(Forward Pass)来获取 π(у|x, θ') 的概率。
成本量化: 假设反向传播成本是前向的2倍,这相当于增加了 25% 的训练成本。
二、FP16 精度
2.1 BF16 与FP16的特征
2.1.1 FP16 vs. BF16 范围与精度
浮点数:
- 指数位(Exponent Bits) 决定可表示数值的范围(数值能有多大或多小)
- 尾数位(Mantissa Bits)(也称为小数位)决定数值的精度(在该范围内能多细致地区分不同数值)
| Property | FP16 | BF16 |
|---|---|---|
| 比特分配 | ||
| 指数位 (Exponent) | 5 bits | 8 bits |
| 尾数位 (Mantissa) | 10 bits | 7 bits |
| 动态范围 (Range) | 有限,易发生上溢/下溢 | 与 FP32 相同,极不易溢出 |
| 最小正数 | 6.1 × 10⁻⁵ | ~1.2 × 10⁻³⁸ |
| 最大正数 | 6.6 × 10⁴ | 3.4 × 10³⁸ |
| 精度 (Precision) 大于 1 的最小值 | 1 + 2⁻¹⁰ ≈ 1.000977 (精度高) | 1 + 2⁻⁷ ≈ 1.007812 (精度低) |
结论: FP16 的精度是 BF16 的 8 倍 (2的3次方)。 在深度神经网络中,数值会经过数以亿次的累加和乘法。精度的微小差异会在层与层之间被放大。
2.1.2 FP16容易上下溢出,利用损失缩放稳定训练
利用损失缩放稳定 FP16 训练是为了解决 FP16 在工程落地中最大的痛点------数值范围不足。容易溢出。
- 下溢 (Underflow) 风险: 在深度神经网络的训练中(尤其是反向传播计算梯度时),梯度值往往非常小(例如 10-9级别)。在 FP16 中,这些微小的梯度会被直接变成 0。如果梯度为 0,模型权重就不会更新,训练就会停滞。
- 上溢 (Overflow) 风险: 虽然较少见,但在某些计算中数值可能超过
6.6 × 10⁴ ,变成 NaN (Not a Number) 或无穷大,导致训练崩溃。
相比之下,BF16 和 FP32 的指数位有 8 位,几乎不存在这个问题。这就是为什么业界之前普遍抛弃 FP16 转向 BF16 的原因。
为了让 FP16 能够胜任训练任务,作者采用了标准的 Loss Scaling 技术。这是一个简单但在混合精度训练中至关重要的技巧。工作原理(三步走):
放大 (Scaling Up): 在进行反向传播之前,将计算出的 Loss(损失值)乘以一个巨大的缩放因子 S(Scaling Factor,例如 210 或更大)。
反向传播 (Backpropagation): 使用放大的 Loss 计算梯度。根据链式法则,计算出的梯度也会被放大 S 倍。
效果: 原本极小的梯度被放大,从而落入 FP16 的可表示范围内,避免了下溢(变成 0)。缩小 (Unscaling): 在利用梯度更新权重之前,将梯度除以 S,还原其真实的数值大小。
然后使用 FP32 格式的主权重(Master Weights)进行更新。
论文指出,为了不需要人工去猜这个因子 S 到底该设多大,通常采用 动态损失缩放 (Dynamic Loss Scaling) 策略:自动调整:
如果检测到梯度计算中出现了 Inf (无穷大) 或 NaN(说明 S 太大导致上溢),则跳过本次更新,并将 S 减半。
如果连续多次迭代都没有出现溢出,则尝试将 S 增大。RL 场景的适配性:
作者强调,在 RL 微调(Post-training)阶段,模型的权重已经经过预训练,数值分布相对稳定,不像从头预训练那样剧烈波动。因此,配合动态 Loss Scaling,FP16 的稳定性完全可以得到保障。
2.1.3 BF16 照搬了 FP32 的指数位, 不再担心溢出,被广泛使用
- BF16 的解法: BF16 设计极其巧妙,它直接照搬了 FP32 的指数位(8位)。 这意味着:凡是 FP32 能表示的数值范围,BF16 都能表示。
- 结果: 开发者不再需要担心数值溢出的问题,训练过程极其稳定。
极简的工程实现(抛弃 Loss Scaling)由于 BF16 解决了范围问题,它带来了一个巨大的工程红利------不再需要 Loss Scaling。
正如 2.2 节所述,FP16 训练必须配合复杂的"损失缩放"技术,还要处理缩放因子动态调整、跳过 NaN 步数等繁琐逻辑。
BF16 是"即插即用"的: 开发者可以像使用 FP32 一样直接运行代码,却能享受减半的显存占用和翻倍的计算速度。这种"无痛迁移"的特性,使得 BF16 迅速在工程界普及。
预训练对精度的"宽容度"这一点非常关键:
- 观察: 在预训练(Pre-training)阶段,模型是在海量数据上学习通用的统计规律。研究发现,预训练过程具有很强的鲁棒性(Robustness),对数值噪声不敏感。
- 结论: 即使 BF16 的尾数精度很低(只有 7 bits,也就是精度较差),但在预训练这种"大力出奇迹"的阶段,这并没有造成明显的性能损失。模型依然能收敛得很好。
2.2 为什么 FP16 是 RL 微调的关键
2.2.1.RL 算法(如 PPO)对微小变化的极度敏感性
与预训练(Supervised Learning)只关心"预测下一个词是否准确"不同,强化学习(RL)关心的是策略的更新幅度。
PPO 的核心机制: PPO(Proximal Policy Optimization)依赖于新旧策略的概率比率 。它是通过限制这个比率不要偏离 1 太远来保证训练稳定的。
- 精度需求: 在训练后期,新旧策略的概率通常非常接近(例如 0.90001 和 0.9002)。
- BF16 的失效: 由于只有 7 位尾数,BF16 可能会把这两个数都截断成
0.9000。导致比率变成 1.0,梯度消失,模型认为不需要更新。
FP16 的优势: FP16 有 10 位尾数,能精准捕捉到这 0.0001 的差异,从而产生有效的梯度信号。
2.2.2. 解决"分布坍缩"与 KL 散度计算问题
RL 训练中通常包含一个 KL 散度(KL Divergence)惩罚项,用来防止模型"忘得太快"或输出分布崩坏。
- KL 散度公式:
- 对数域的放大效应: 公式里包含对数运算。如果 P 和 Q 在低精度下被舍入成相同的值,log(1)= 0,KL 惩罚项直接失效。
- 后果: 如果 KL 算不准,Reward Model 给出的奖励信号可能会导致模型迅速过拟合到某个错误的模式上,或者训练极其不稳定。FP16 的高精度保证了 KL 散度计算的准确性,维持了训练的"约束力"。
2.2.3. 权衡:用"范围"换"精度"是值得的
作者在这里做了一个关键的价值判断(Trade-off):
- 承认 FP16 的缺点: 作者不否认 FP16 动态范围小(容易溢出)。这意味着使用 FP16 必须配合 Loss Scaling(损失缩放) 技术,工程实现上比 BF16 麻烦。
- 强调 RL 的特性: 但是,在 RL 微调阶段,梯度的数值范围通常没有预训练那么夸张(没有那么大的方差),反而是梯度的细腻程(Precision)更为致命。
- 结论: 为了获得那 2-10 的精度(比 BF16 高 8 倍),去承担 Loss Scaling 的工程成本是完全值得的。
2.3 离线分析--不同模型不同推理精度效果
为了定量地验证精度差异的影响,作者进行了一项离线分析。
使用 Llama-2-7B-Chat 模型,并在相同的输入提示(prompt)下比较了不同精度格式产生的对数概率(log-probabilities)。将全精度(FP32)下的结果视为Ground Truth。
| dtype | AMC23 (8K) | AIME24 (8K) | AMC23 (32K) | AIME24 (32K) |
|---|---|---|---|---|
| BF16 | 50.38 | 22.60 | 62.35 | 29.90 |
| FP16 | 50.60 | 20.10 | 63.10 | 30.94 |
| FP32 | 51.54 | 22.30 | 62.42 | 28.44 |
- FP16 的表现: 结果表明,FP16 的相对误差极低(大约在10-5 量级),这说明 FP16 在表示模型输出分布时几乎是无损的,与 FP32 非常接近。
- BF16 的表现: 相反,BF16 的相对误差要大得多(大约在 10-2 量级)。
这种显著的误差在强化学习(RL)背景下是致命的。PPO 算法依赖于新旧策略之间的概率比率(probability ratios)。
当策略更新非常微小时(这在微调后期很常见),BF16 较大的相对误差可能会:
- 完全掩盖真实的策略变化信号(梯度消失)
- 引入巨大的噪声,导致 KL 散度计算失真
- 造成价值估计(Value Estimation)的严重偏差
因此,从离线分析可以清晰看出:BF16 的尾数精度不足以支撑 RL 微调阶段所需的细粒度计算,而 FP16 则表现出明显更高的稳定性与可靠性,是更合适的选择。
2.4 评估强化学习算法--健全性测试
为了更严格地评估强化学习(RL)算法的可靠性与鲁棒性,作者提出了一种新颖的 健全性测试(Sanity Test)。
传统基准测试往往混杂了对初始模型而言过于简单(Trivial)或彻底无法解决(Unsolvable)的问题。前者会消耗额外计算资源,后者则带来显著歧义:一旦模型表现欠佳,很难判断问题出在算法能力不足,还是模型本身的表达能力就不足以解决该任务。
Sanity Test 的设计目标正是高效消除这种模糊性。
作者通过构建一个 "可完善数据集(Perfectible Dataset)" 解决这一难题:该数据集中的每个问题都已知可解,但同时并非轻而易举即可完成。通过在这样的数据集上训练,可以清晰评估 RL 算法能否真正挖掘模型的潜在能力。理论上,一个可靠的 RL 算法应当能够在该数据集上将训练准确率提升至 100%。
构建该数据集的方法如下:作者对 MATH 数据集的每个问题生成 40 个模型回复,并仅保留初始准确率介于 20% 至 80% 的题目。
最终,针对 DeepSeek-R1-Distill-Qwen-1.5B 模型得到一个包含 1,460 个问题的目标数据集。
为此测试,作者设定了一个清晰的通过标准:若某 RL 算法在该数据集上的训练准确率能够收敛至高阈值(例如 95%)以上,则视为通过。
反之,若无法达到该标准,则可认为该算法不够可靠,甚至可能在设计上存在根本性问题。
需要强调的是,通过 Sanity Test 并不保证算法在所有任务上都能成功,但测试失败几乎可以视为算法存在重大缺陷的重要证据。
2.4.1 实验设置
- 基础模型与硬件环境
初始模型:使用 DeepSeek-R1-Distill-Qwen-1.5B 作为初始模型。
上下文长度:设置为 8,000。
硬件配置:所有实验均在 8张 NVIDIA A100 80G GPU 上运行。- 训练参数配置
Batch Size:64
Rollouts:每个问题进行 8 次采样- 超参数设置
GRPO 系列算法:
clip_higher 参数默认设置为 0.28。
重要性采样(Importance Sampling)方法:
裁剪阈值(Clipping threshold,即公式中的 )设置为 3。- 评估的算法列表
Vanilla GRPO (Dr.GRPO): 作为基线方法,具体使用的是 Dr.GRPO 变体,该变体去除了原始 GRPO 中的长度和难度偏差。
GRPO with Token-level TIS: token 级重要性采样
GRPO with Sequence-level MIS: 序列级重要性采样。
Standard Policy Gradient (PG-Seq-IS): 带有重要性采样的标准策略梯度算法
GSPO:虽然 GSPO 主要是为解决混合专家模型(MoE)的不匹配问题而设计的,但也包含在本次实验中进行对比。
2.4.2 FP16 vs BF16算法修正
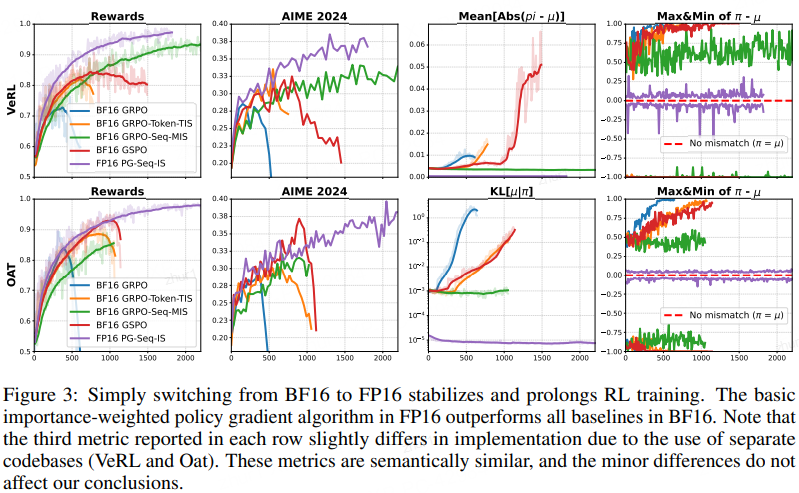
作者主要通过在 VeRL 和 Oat 两个不同的框架下进行实验,对比了现有的旨在解决"训练-推理不匹配"的算法(通常使用 BF16)与本文提出的 FP16 方案的效果。
多框架验证(Framework Validation)
为了确保结论的鲁棒性并排除特定实现带来的干扰,作者在两个独立的框架上进行了测试:VeRL 和 Oat。结果显示,现有方法在 BF16 精度下的不稳定性在两个框架中是一致的。
现有算法在 BF16 下的表现(不稳定性与局限性)
图2: FP16 vs BF16算法修正
作者测试了多种算法在 BF16 下的表现,发现了普遍的训练崩溃(Training Collapse)或性能瓶颈:
- BF16 GRPO (基线):
表现:训练早期就会崩溃。
数据:在 VeRL 中最高准确率仅达到 73%,在 Oat 中为 84%,随后性能便开始下降。- BF16 GRPO-Token-TIS:
表现:虽然比普通 GRPO 稍微延长了训练时间,但最终仍然失败。
数据:在达到 82% (VeRL) 和 88% (Oat) 的准确率后崩溃。- BF16 GSPO:
表现:令人惊讶的是,尽管它完全不使用推理策略 ,但在 BF16 下比 Token-level TIS 更稳定。
问题:在 VeRL 实验中,GSPO 的梯度范数在 1200 步后变为 NaN,导致更新停止。- BF16 GRPO-Seq-MIS:
表现:这是在 BF16 下唯一没有崩溃的算法。
缺陷:
收敛慢:因为序列级比率的方差很高。
性能有上限(部署差距):最高训练准确率仅 95%(FP16 为 99%),AIME 2024 得分 34%(FP16 为 39%)。这证明它虽然稳定,但无法完全消除不匹配带来的性能损失。
FP16 精度的有效性(The Efficacy of FP16)与BF16对比
与上述复杂的算法修正相比,简单地将训练和推理精度从 BF16 切换到 FP16 带来了巨大的提升:
- 全面提升:FP16 训练更稳定、收敛更快、最终奖励和评估分数更高。
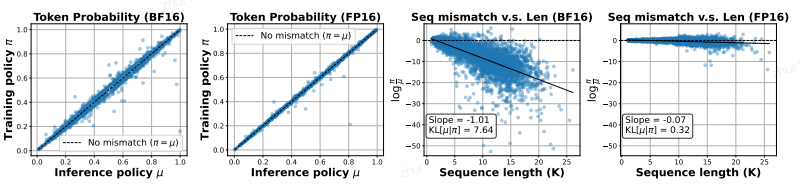
- 核心发现:FP16 能够从根本上改善重要性采(Importance Sampling)的行为。
在 BF16 下方差极大的"序列级比率(sequence-level ratio)",在 FP16 下变得更加集中和稳定。
- 回归本源:由于 FP16 带来的数值稳定性,作者发现最基础、无偏的策略梯度算法(Standard Policy Gradient,公式 5) 在搭配 FP16 使用时,其表现优于所有在 BF16 下运行的复杂算法修正(如 TIS/MIS)。
训练动态分析(Training Dynamics)崩溃预警
作者观察到了一个有趣的现象,可以作为训练崩溃的"早期预警":
- 崩溃前兆:那些最终崩溃的算法,在崩溃前都会表现出不断增长的"训练-推理不匹配"。
- 极端分化:策略差异 π(·|θ′)−μ(·|θ′) 会收敛到极端值(一个策略概率趋近 1,另一个趋近 0),尽管它们使用的是同一份权重。
- FP16 的优势:FP16 训练所展现出的不匹配程度远低于任何 BF16 方法,这种内在的稳定性解释了为什么简单的策略梯度在 FP16 下能胜过复杂的算法。
框架间的细微差异
尽管核心结论一致,但两个框架表现略有不同:
- Oat 稍好:Oat 框架中的初始不匹配程度略小于 VeRL(-0.9 vs -1.0),且训练奖励稍高。
- VeRL 波动:即使在 FP16 下,VeRL 也更容易出现偶尔的数值尖峰。
- 原因推测:这可能归因于它们使用的分布式后端不同(Oat 使用 PyTorch FSDP,VeRL 使用 DeepSpeed ZeRO)。
总结:这一节通过详实的实验数据证明,现有的算法修补方案在 BF16 下要么崩溃,要么有性能瓶颈;而简单地切换到 FP16 不仅解决了稳定性问题,还让最基础的 RL 算法发挥出了超越复杂方法的性能。
2.4.3 在 FP16 下重新审视不同的 RL 算法
这一节主要探讨了当底层精度切换为 FP16 后,那些原本表现各异的强化学习算法(如 GRPO, TIS, MIS 等)在性能上发生了什么变化。
算法性能趋于一致(Performance Convergence)
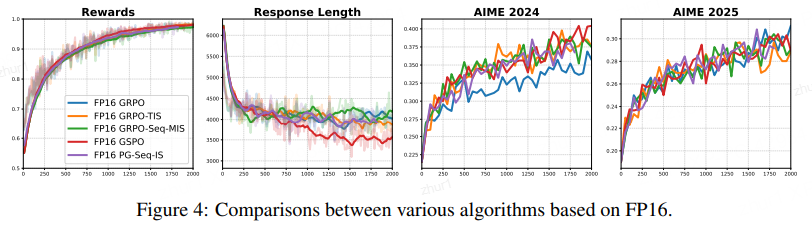
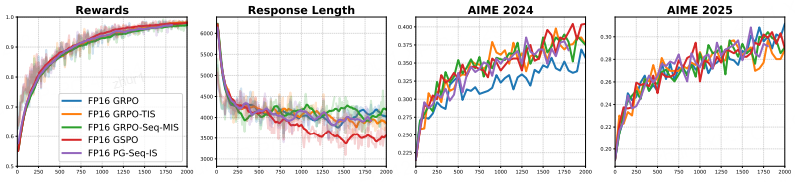
观察结果:当所有算法都使用 FP16 进行训练时,它们之间的性能差异变得几乎无法区分(如图 4 所示)。
对比反差:这与 BF16 下的情况截然不同(在 BF16 下,有些算法会崩溃,有些则勉强维持,差异巨大)。
- 原因分析
作者将这种性能趋同归因于 FP16 显著减少了训练-推理不匹配(Training-Inference Mismatch):
近似在线策略(Nearly On-policy):由于 mismatch 大幅降低,优化问题实际上被转化为了一个近似"在线策略(on-policy)"的设定(即训练策略 和推理策略 数值上几乎一致)。
修正失效:在这种状态下,各种算法原本为了修正 mismatch 而设计的复杂机制(如重要性采样比率截断等)就变得多余了,无法提供额外的收益。
3. 细微的例外情况
GRPO 的表现:作者观察到一个小例外,原始的 GRPO 算法在 AIME 2024 基准测试中的得分略低。
非决定性结论:然而,该算法在 AIME 2025 上的得分却又略高。因此,很难得出它比其他算法差的确定性结论。
总结:这一节的核心观点是,一旦使用 FP16 解决了根本的精度问题,具体的算法选择就变得不再重要。复杂的算法修正不再带来优势,因为它们试图解决的"不匹配"问题在 FP16 下已经基本不存在了。
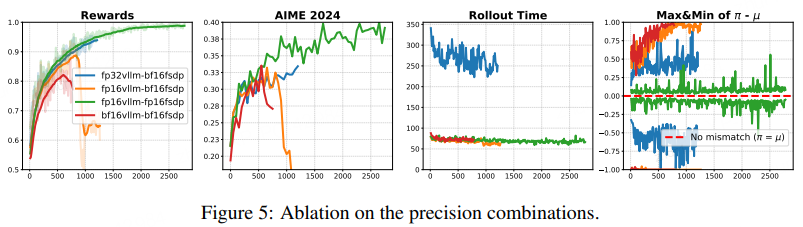
2.4.4 精度消融实验
实验在 VeRL 框架下进行,使用 vLLM 进行推理,PyTorch FSDP 进行训练。
固定或改变训练与推理的精度组合(例如:训练用 BF16,推理用 FP32 等),以观察结果变化(见图 4)。
当固定使用 BF16 进行训练时,作者发现:
- 提高推理精度有帮助:单纯提高推理(Inference)的精度,就能延长训练的稳定性并提升性能。
- FP32 推理能稳定训练:当组合为"BF16 训练 + FP32 推理"时,训练过程变得完全稳定,没有出现崩溃(Collapse)迹象。
- 致命缺陷(效率低):虽然 FP32 推理能解决稳定性问题,但代价极其高昂。FP32 的推理速度比 FP16 或 BF16 慢了近 3 倍,这使得该方案在实际的大规模实验中完全不可行。
当使用 FP16 同时进行训练和推理时,效果最好:
- 最低的不匹配:这种组合产生了最小的训练-推理数值不匹配。
- 最佳稳定性与性能:展现了最稳定的训练动态,并在完美数据集(perfectible dataset)上达到了接近 100% 的训练准确率。
- 高效率:最重要的是,它在获得上述稳定性的同时,没有牺牲任何速度(与 BF16 效率相当)。
这一节的消融实验证实了:虽然提高推理精度(如用 FP32)可以作为一种补救措施来稳定 BF16 训练,但由于效率太低而不实用。相比之下,全流程使用 FP16 是在稳定性、性能和计算效率三者之间取得平衡的最优解。
2.5 FP16训练泛化性
2.5.1 扩展到更大的模型
这一节探讨了当模型架构不同或参数量显著增大时,BF16 的不稳定性是否依然存在。
测试模型:
Llama-3-8B-Instruct(不同架构)
Qwen-2.5-32B-Instruct(更大参数量)
实验结果:
Llama-3-8B:在 BF16 下,训练开始后不久就会崩溃(Collapse),奖励降至 0;而在 FP16 下,训练稳定且性能持续提升。
Qwen-2.5-32B:结果更为惊人。由于模型更大,累积的数值误差更严重。在 BF16 下,训练在第 0 步(Step 0)就直接崩溃了;相比之下,使用 FP16 能够完美训练,在 GSM8K 上达到了 96% 的准确率,在 AIME 上达到了 50%。
- 核心结论:模型越大,BF16 带来的数值不稳定性越严重。这意味着对于未来更大规模的模型,使用 FP16 进行 RL 训练可能不仅仅是一个选项,而是一个必要条件。
2.5.2泛化到更难的任务
这一节探讨了该方法在比 GSM8K 更难的数学推理任务上的表现。
测试数据:MATH-500
实验现象:
BF16:训练迅速崩溃。
FP16:训练非常稳定,最终达到了 65.6% 的准确率,这一成绩与专门针对数学优化的 SOTA 模型(如 Qwen-2.5-Math-7B)相当。
- 深入发现:作者观察到,在更难的 MATH-500 数据集上,"训练-推理不匹配(Mismatch)"的程度实际上比在 GSM8K 上更大。尽管如此,FP16 依然能够有效地缓解这种不匹配,支撑模型完成高质量的学习。
2.5.3 泛化到 PPO 算法
前文主要关注 GRPO,这一节将验证范围扩展到了经典的 PPO算法。PPO 与 GRPO 的主要区别在于 PPO 需要训练一个额外的 Critic(价值模型)。
实验设置:使用 PPO 进行训练,Critic 模型由 Policy 模型初始化。
实验结果:
BF16:
KL 散度爆炸:KL 散度(衡量新旧策略差异的指标)迅速飙升到 > 40 的极高值。
Value Loss 激增:价值函数的损失也急剧上升。
这导致 PPO 训练完全失败。
FP16:
KL 散度保持在合理的低水平。
Value Loss 稳定下降。
训练过程平稳且收敛。
- 核心结论:这一发现极具启发性。PPO 长期以来被认为是一个对超参数极度敏感、极难调优的算法。作者指出,PPO 过去许多"难以训练"或"不稳定"的情况,很可能根本不是超参数的问题,而是由于底层使用了 BF16 导致的数值精度问题。
通过全方位的实验证明了: 无论是更换模型架构(Llama)、增加模型规模(32B)、挑战更难的数据集(MATH-500),还是切换RL 算法(PPO),BF16 导致的训练崩溃都是普遍存在的,而 FP16 则是通用的、稳健的解决方案。