【NLP】one-hot到word2vec发展路线

文章目录

一、图像领域的预训练
- 1.概念
- - [1.1 Frozen](#1.1 Frozen)
  - [1.2 Fine-Tuning（微调）](#1.2 Fine-Tuning（微调）)
  - [1.3 预训练的好处](#1.3 预训练的好处)
  - 1.4常用的预训练模型：ImageNet
二、NLP发展史
- [1. 传统的NLP：one-hot编码](#1. 传统的NLP：one-hot编码)
- [2. 语言模型问题背景及基本思想](#2. 语言模型问题背景及基本思想)
- [3. NNLM神经网络语言模型](#3. NNLM神经网络语言模型)
- 3.Word2Vec的诞生
- - [3.1 改进](#3.1 改进)
  - [3.1 两种核心模型](#3.1 两种核心模型)
  - - （1）CBOW-词袋
    - （2）Skip-gram
  - [3.2 两种优化算法](#3.2 两种优化算法)
  - - [（1）Hierarchical Softmax（层次Softmax）](#（1）Hierarchical Softmax（层次Softmax）)
    - [（2）Negative Sampling（负采样）](#（2）Negative Sampling（负采样）)
    - - 重新计算词频
      - 神来之笔：将多分类问题转变为二分类问题

一、图像领域的预训练

1.概念

先用某个训练集合比如训练集合A或训练集合B，对网络进行预训练，在A或B任务上训练网络参数，然后存起来备用，面临第三个任务C时，应用相同的网络结果，在比较浅层的网络结果中，使用在A或B任务上学习好的参数，其他CNN高层参数仍然随机初始化，然后用C任务的训练数据来训练网络，此时有两种方法：

1.1 Frozen

浅层加载的参数在训练C任务过程中不动

复制代码

**Frozen体现在对所有的预训练参数，让他们不参与梯度下降训练过程，只替换并训练最后的分类头。**

```python
# 冻结所有预训练参数
for param in model.parameters():
    param.requires_grad = False

# 只替换并训练最后的分类头
model.fc = nn.Linear(num_ftrs, 10)
# 此时，优化器只对新分类头的参数进行更新
optimizer = optim.SGD(model.fc.parameters(), lr=1e-3, momentum=0.9)

使用场景：

下游任务数据集非常小（容易过拟合）。
计算资源有限，训练速度快。
预训练模型的特征非常通用，与下游任务高度相关（例如，用ImageNet预训练模型做其他动植物分类）。
作为一个快速的性能基线

1.2 Fine-Tuning（微调）

解冻预训练模型主干的全部或部分参数，让它们和新分类头一起参与训练。通常为主干设置比分类头更小的学习率，以防止预训练好的特征被破坏性地更新。

python 复制代码

optimizer = optim.SGD([
    {'params': model.fc.parameters(), 'lr': 1e-3},           # 新分类头：大学习率
    {'params': (p for n, p in model.named_parameters() if 'fc' not in n), 'lr': 1e-4} # 预训练主干：小学习率
], momentum=0.9)

应用场景：

下游任务数据集足够大。
下游任务与预训练任务的数据分布存在一定差异（例如，用ImageNet自然图像预训练模型去处理医学X光片）。
计算资源充足。
通常能获得比冻结方法更高的性能上限。

1.3 预训练的好处

如果训练集比较少的话，直接使用当前神经网络Resnet、Densenet和Inception等网络时，模型的参数会达到百万、千万甚至上亿的个数，但数据量比较少的情况下做这样的训练效果不一定好，这很容易造成过拟合。但是在已经训练好参数的ImageNet上学习数据集少的可怜的C任务，再通过Fine-Funing调整参数就会让它更加适合解决C任务。

1.4常用的预训练模型：ImageNet

训练数据足够大。训练了大量提前标注好的数据集，训练数据越大，模型参数越靠谱；
数据图像类别多，种类越多，模型越具有通用性。

二、NLP发展史

1. 传统的NLP：one-hot编码

One-hot编码是一种词表示方法，它为基于统计的NLP模型（如n-gram模型）提供了基础的数值化表示，使得基于最大似然估计的概率计算得以实现。具体思想如下：

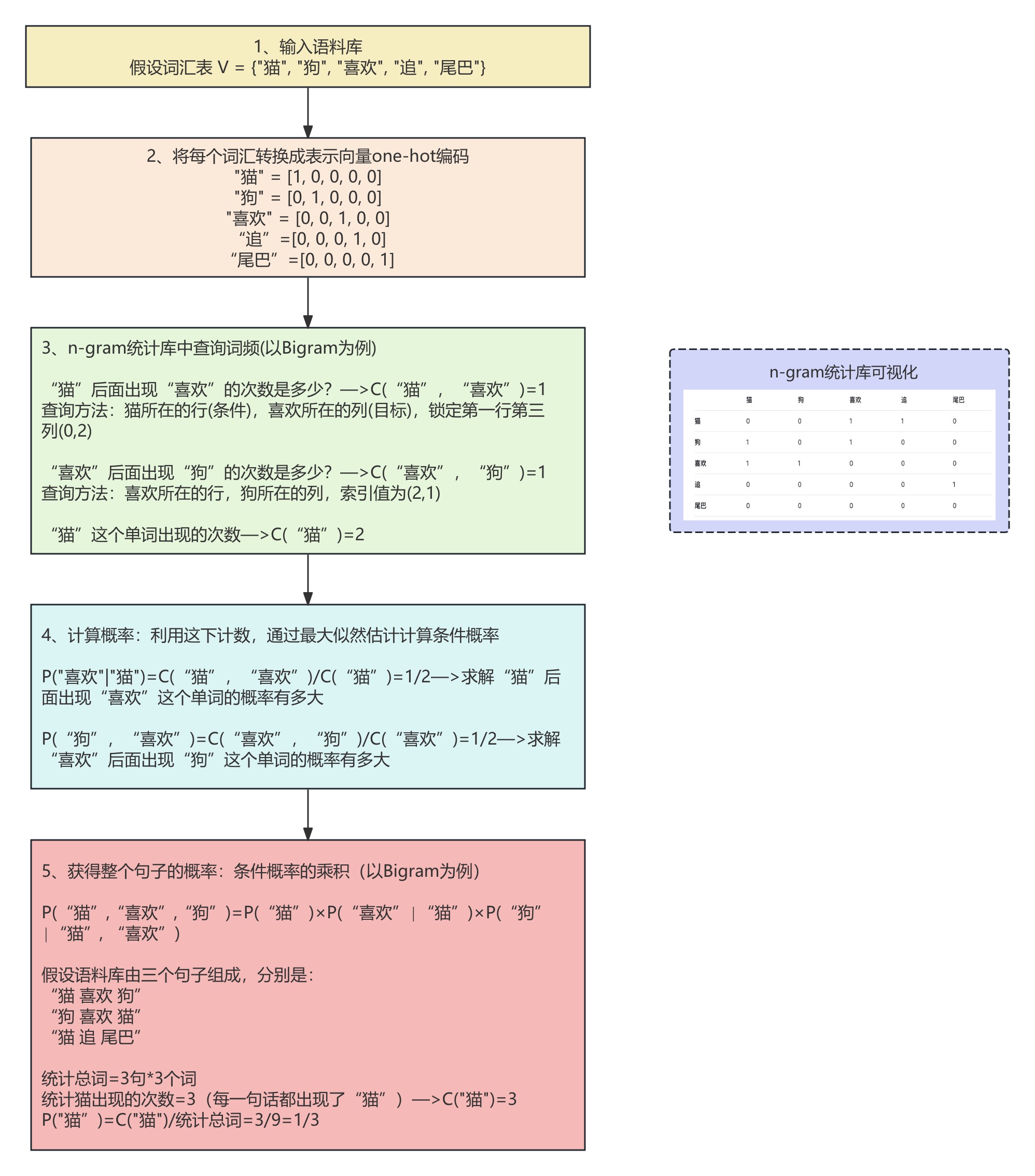
存在的问题：

（1）数据维度高，计算效率低。

（2）在计算相似度时（余弦相似度或者是欧式距离），向量正交产生，词汇鸿沟，无法理解到语义，只能粗暴得判定这两个单词是否是同一个词。

2. 语言模型问题背景及基本思想

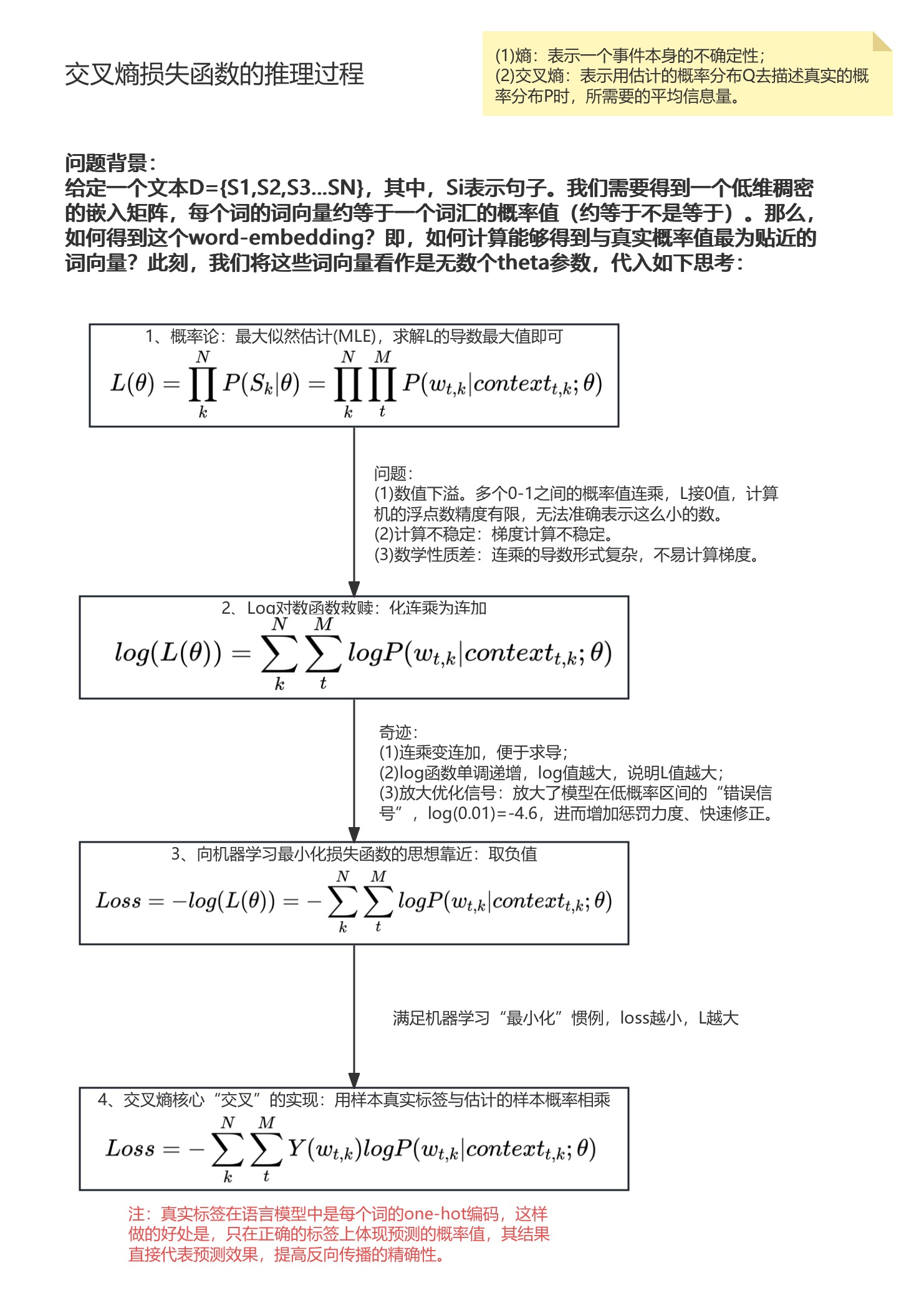
特征	传统NPL(one-hot+统计)	特征
核心思想	统计共现频率	学习分布式表示
词表示	one-hot(稀疏/高维/离散)	词向量(稠密/低维/连续)
工作原理	查找统计表，计算条件概率	通过神经网络计算条件概率
泛化能力	弱	强
例子	没见过"猫"追"球"，就认为概率为0	知道"猫"近似于"狗"，"尾巴"近似于"球"推断出"猫"追"球"是合理的。

3. NNLM神经网络语言模型

提出了嵌入矩阵，初始化了一个嵌入矩阵，维度为（词汇长度，嵌入维度），将原来超高维度的向量矩阵大幅度降维。预测目标：用前n-1个单词预测第n个单词时，每一个词向量都去找到其对应的嵌入向量，然后通过正向传播，让模型进行预测，接着利用反向传播惩罚参数，最终得到一个能够包含语义关系的嵌入矩阵------能够表示单词之间的相似性。

NNLM的基本架构：

输入层：将前 n-1 个单词（作为上下文）通过查找表（Look-up Table）转换为密集向量（即词向量，Word Embedding）。这一步是NNLM的一个重要贡献，它首次将离散的单词映射到了连续的向量空间。
投影层：将上一步得到的多个词向量拼接（concatenate）成一个巨大的输入向量。
隐藏层：一个标准的全连接层，使用tanh等激活函数。
输出层：一个更大的全连接层，接一个softmax函数，用于预测词汇表中所有单词作为下一个单词的概率。

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
# 计算词之间的余弦相似度
from torch.nn.functional import cosine_similarity

# 设置随机种子以保证结果可重现
torch.manual_seed(42)

# 定义超参数
vocab = ["我", "爱", "人工智能"]  # 词汇表
vocab_size = len(vocab)          # 词汇表大小
embedding_dim = 2                # 嵌入维度
context_size = 1                 # 上下文长度（用前1个词预测下一个词）
hidden_dim = 3                   # 隐藏层维度
learning_rate = 0.1
epochs = 50                      # 训练轮数


# 创建词到索引的映射
word_to_ix = {word: i for i, word in enumerate(vocab)}
print("词汇映射:", word_to_ix)
#词汇映射: {'我': 0, '爱': 1, '人工智能': 2}

# 训练数据: 用前一个词预测后一个词
# 输入: ["我"] -> 目标: "爱"
# 输入: ["爱"] -> 目标: "人工智能"
training_data = [
    (["我"], "爱"),
    (["爱"], "人工智能")
]


# 将文本数据转换为索引
def make_context_vector(context, word_to_ix):
    idxs = [word_to_ix[w] for w in context]
    return torch.tensor(idxs, dtype=torch.long)

# 准备训练数据
X_train = []
y_train = []
for context, target in training_data:
    context_vector = make_context_vector(context, word_to_ix)
    target_index = word_to_ix[target]
    X_train.append(context_vector)
    y_train.append(target_index)

print("训练数据准备完成")
print("输入:", [vocab[x.item()] for x in X_train])
print("目标:", [vocab[y] for y in y_train])


class NNLM(nn.Module):
    def __init__(self, vocab_size, embedding_dim, context_size, hidden_dim):
        super(NNLM, self).__init__()
        '''
        vocab_size------>词汇表大小
        embedding_dim------>嵌入维度
        context_size------>上下文长度（用前1个词预测下一个词）
        hidden_dim------>隐藏层维度
        '''
        self.context_size = context_size

        # 词嵌入层 - 这就是我们要学习的词嵌入矩阵！
        self.embeddings = nn.Embedding(vocab_size, embedding_dim)

        # 线性层和激活函数
        self.linear1 = nn.Linear(context_size * embedding_dim, hidden_dim)
        self.tanh = nn.Tanh()
        self.linear2 = nn.Linear(hidden_dim, vocab_size)

        # 打印初始化的词嵌入矩阵
        #print(self.embeddings.weight)
        print("初始词嵌入矩阵:")
        for i, word in enumerate(vocab):
            print(f"  {word}: {self.embeddings.weight[i].detach().numpy()}")

    def forward(self, inputs):
        # 1. 查找词嵌入 (batch_size, context_size) -> (batch_size, context_size, embedding_dim)
        embeds = self.embeddings(inputs)
        #print(embeds)

        # 2. 拼接嵌入向量 (batch_size, context_size * embedding_dim)
        embeds = embeds.view(embeds.shape[0], -1)


        # 3. 通过隐藏层
        out = self.linear1(embeds)
        #print(out)
        #print(out.shape)
        out = self.tanh(out)


        # 4. 输出层
        out = self.linear2(out)
        #print(out)
        #print(out.shape)
        log_probs = torch.log_softmax(out, dim=1)
        return log_probs


# 创建模型
model = NNLM(vocab_size, embedding_dim, context_size, hidden_dim)

loss_function = nn.NLLLoss()  # 负对数似然损失
optimizer = optim.SGD(model.parameters(), lr=learning_rate)


print("\n开始训练...")
for epoch in range(epochs):
    total_loss = 0

    for context, target in zip(X_train, y_train):
        # 准备输入数据
        context_var = context.unsqueeze(0)  # 添加batch维度

        # 前向传播
        model.zero_grad()
        log_probs = model(context_var)

        # 计算损失
        loss = loss_function(log_probs, torch.tensor([target]))

        # 反向传播
        loss.backward()
        optimizer.step()

        total_loss += loss.item()

    # 每10轮打印一次进度
    if (epoch + 1) % 10 == 0:
        print(f'Epoch {epoch + 1}/{epochs}, Loss: {total_loss / len(X_train):.4f}')

print("训练完成！")

print("\n训练后的词嵌入矩阵:")
final_embeddings = model.embeddings.weight.detach()
for i, word in enumerate(vocab):
    print(f"  {word}: {final_embeddings[i].numpy()}")

# 计算词之间的余弦相似度
from torch.nn.functional import cosine_similarity

print("\n词嵌入相似度:")
for i in range(vocab_size):
    for j in range(i + 1, vocab_size):
        sim = cosine_similarity(
            final_embeddings[i].unsqueeze(0),
            final_embeddings[j].unsqueeze(0)
        ).item()
        print(f"  '{vocab[i]}' 和 '{vocab[j]}' 的相似度: {sim:.4f}")


def predict_next_word(model, context_words):
    context_vector = make_context_vector(context_words, word_to_ix)
    context_var = context_vector.unsqueeze(0)

    with torch.no_grad():
        log_probs = model(context_var)
        probs = torch.exp(log_probs)

    print(f"\n输入: '{' '.join(context_words)}'")
    for i, word in enumerate(vocab):
        print(f"  预测 '{word}' 的概率: {probs[0][i]:.4f}")

    predicted_index = torch.argmax(probs[0]).item()
    return vocab[predicted_index]


# 测试预测
test_context = ["我"]
predicted_word = predict_next_word(model, test_context)
print(f"  最可能的下一个词: '{predicted_word}'")

test_context = ["爱"]
predicted_word = predict_next_word(model, test_context)
print(f"  最可能的下一个词: '{predicted_word}'")

存在的问题：

计算复杂度极高：因为Softmax需要计算所有词汇（通常是数万甚至数十万）的得分并归一化为概率。这使得模型的训练和推理速度非常慢。隐藏层的巨大参数量也带来了计算负担。
结构复杂：模型包含了投影层、隐藏层、输出层等多个非线性变换层。复杂的结构意味着更长的训练时间和更多的调参工作。
核心目标不同：NNLM的首要目标是训练一个更好的语言模型（即更准确地预测下一个词），其副产品才是词向量。它的优化过程是为了最小化困惑度（Perplexity），而不是为了得到最优质的词向量。

3.Word2Vec的诞生

3.1 改进

（1）目标转变：放弃完整的语言模型建模。Word2Vec不再以预测下一个单词的概率分布作为核心目标，而是直接专注于学习高质量的词向量。通过更简单高效的任务来达成这个目的；

（2）效率优先：通过简化结构（去掉隐藏层）和优化训练目标（如使用负采样或层次Softmax来避免完整的计算），使得模型可以在大规模语料上进行高效训练。NNML需要对每一个单词计算概率值，当文本量过大时，这样的计算量是灾难性的。

（3）"一个词由其上下文决定"：基于假设分布------相同含义的词会出现在相似的上下文中，Word2Vec通过捕捉单词的上下文关系来学习词向量。

总结：Word2Vec为了高效训练处高质量词向量，甩掉了NNLM做概率预测而产生的沉重包袱。

3.1 两种核心模型

	CBOW-词袋	Skip-gram
目标	通过上下文来预测中心词。	与CBOW相反，通过中心词来预测其上下文。
过程	将上下文多个词的词向量平均（或拼接后投影），直接输入输出层来预测中心词。	输入中心词，输出层试图同时预测多个上下文词。
特点	训练速度快，对高频词效更好。	在小型数据集上效果好，尤其能很好地处理低频词。

（1）CBOW-词袋

目标：通过上下文来预测中心词。

过程：将上下文多个词的词向量平均（或拼接后投影），直接输入输出层来预测中心词。

特点：训练速度快，对高频词效更好。

（2）Skip-gram

目标：与CBOW相反，通过中心词来预测其上下文。

过程：输入中心词，输出层试图同时预测多个上下文词。

特点：在小型数据集上效果好，尤其能很好地处理低频词。

3.2 两种优化算法

为了避免完整的Softmax计算，Word2Vec引入两种革命性技术：

（1）Hierarchical Softmax（层次Softmax）

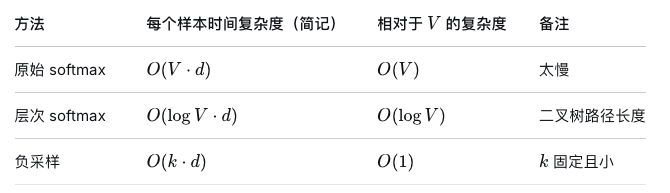
如何基于Huffman树把预测的复杂度从O(V)降到O(logV)？

普通的softmax计算过程

以CBOW模型为例，首先需要通过逻辑回归来计算每个单词的得分，然后通过softmax进行归一化计算（Softmax本身就是一个激活函数）。用公式则可以表示为：

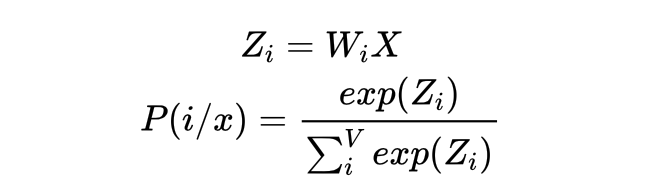
其中，X表示为上下文词向量的平均（或拼接），Wi表示需要预测的中心词的词向量。在Word2Vec中很巧妙得涉及：需要对Win和Wout进行学习，同步输出两个词嵌入矩阵。这是word2vec的创新性之一，认为同一个单词作为预测中心词和上线文本来说，其词向量是不同的。如下所示：

python 复制代码

# 初始化（随机值）
W_in = {
    "the": [0.1, -0.2, 0.3],    # 输入向量
    "cat": [-0.1, 0.3, 0.2],
    "sat": [0.2, -0.1, 0.4],
    "on": [0.3, 0.1, -0.2],     # 也会被更新（如果作为上下文时）
}

W_out = {
    "the": [0.2, -0.1, 0.3],    # 输出向量
    "cat": [-0.2, 0.2, 0.1],
    "sat": [0.1, -0.2, 0.3],
    "on": [-0.1, 0.3, -0.2],    # 目标词的输出向量
}

# 前向传播
x = (W_in["the"] + W_in["sat"]) / 2  # 上下文平均
# 计算"on"的得分
score_on = dot(W_out["on"], x)  # W_out["on"] · x

# 计算损失，反向传播...
# 梯度会更新：
# 1. W_out["on"]（因为它是目标词）
# 2. W_in["the"] 和 W_in["sat"]（因为它们是上下文）
# 3. 其他词的输出向量也会有轻微更新（负采样时）

因此时间复杂度为：O(V)

HierarchicalSoftmax基本思想

将一次巨大的多分类（从 V 个词中选1个）转化为沿着哈夫曼树从根到叶的多次二分类决策。

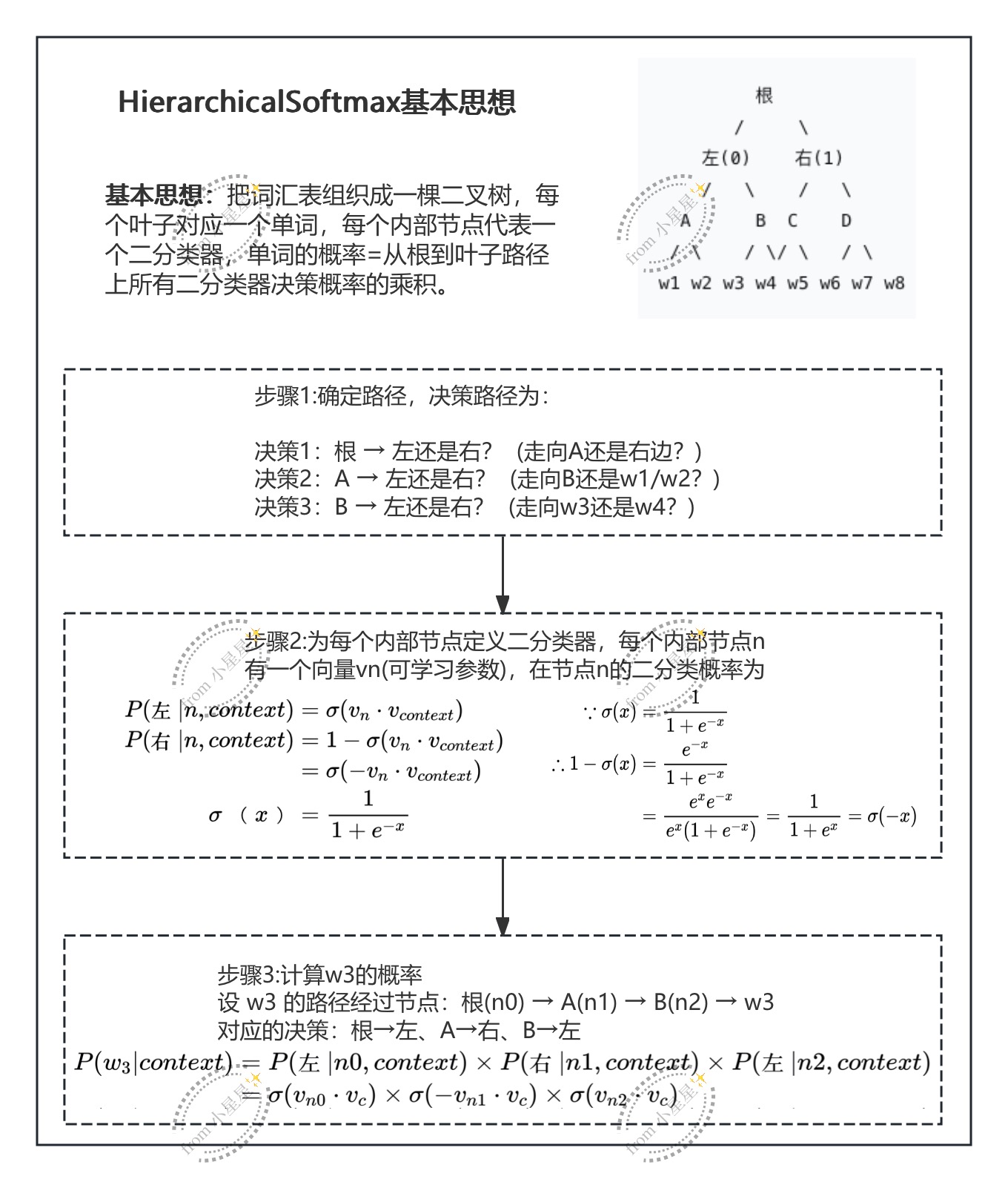
python 复制代码

class HierarchicalSoftmax:
    def __init__(self, vocab_size, embedding_dim):
        # 构建霍夫曼树
        self.tree = build_huffman_tree(word_frequencies)
        # 每个内部节点有一个向量
        self.node_vectors = nn.Embedding(num_internal_nodes, embedding_dim)
    
    def forward(self, context_vector, target_word_id):
        # 1. 找到目标词的路径
        path = self.tree.get_path(target_word_id)  # 例如: [(node1, left), (node2, right), ...]
        
        total_log_prob = 0
        # 2. 遍历路径上的每个节点
        for node_id, is_left in path:
            node_vec = self.node_vectors(node_id)
            score = torch.dot(node_vec, context_vector)
            
            if is_left:
                prob = torch.sigmoid(score)  # P(左|node)
            else:
                prob = torch.sigmoid(-score)  # P(右|node) = 1 - σ(score)
            
            total_log_prob += torch.log(prob)
        
        # 3. 损失
        loss = -total_log_prob
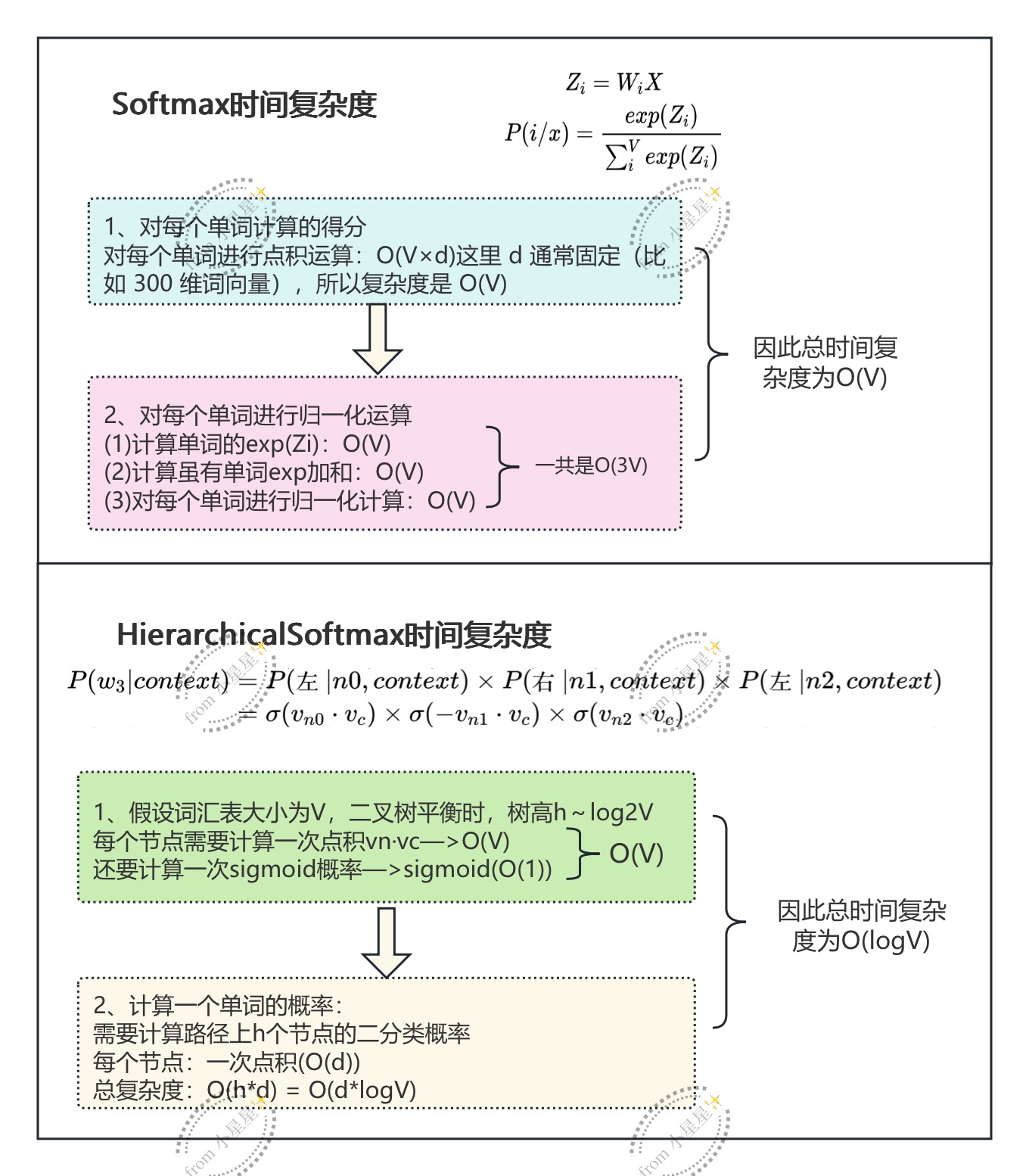
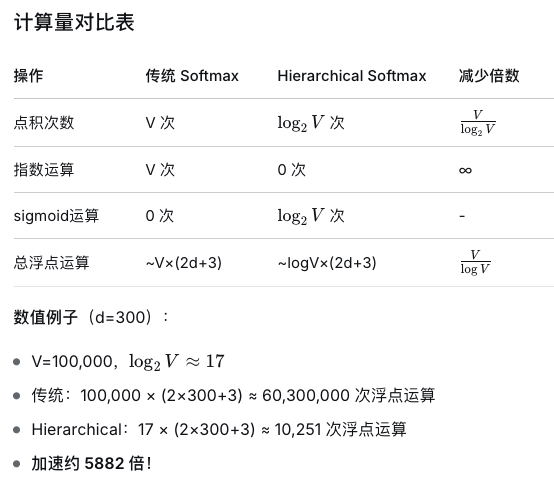
        return loss

Softmax和HierarchicalSoftmax时间复杂度比较

HierarchicalSoftmax的局限性

（1）低频词惩罚：低频词路径长，更新梯度会被稀释；

（2）实现复杂：需要维护树结构；

（3）内存：需要存储内部节点向量（约v-1个）；

（4）现代替代品：负采样更简单，更常用。

（2）Negative Sampling（负采样）

重新计算词频

在正常统计词频的基础上，对每个单词的词频进行3/4幂计算，即：

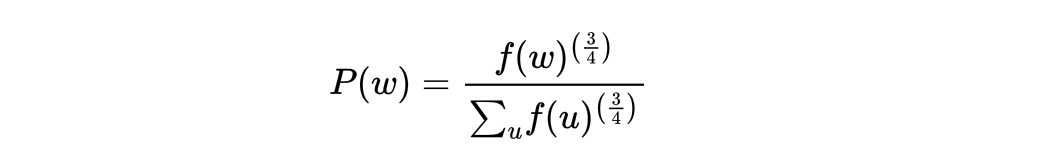
python 复制代码

词频分布示例：
"the":    0.1
"cat":    0.01  
"bed":    0.001
"zygote": 0.00001

采样概率对比：
词        频率     均匀采样   按频率    3/4次幂
-------------------------------------------------
the      0.1      0.00001    0.1      0.056
cat      0.01     0.00001    0.01     0.032
bed      0.001    0.00001    0.001    0.018
zygote   0.00001  0.00001    0.00001  0.001

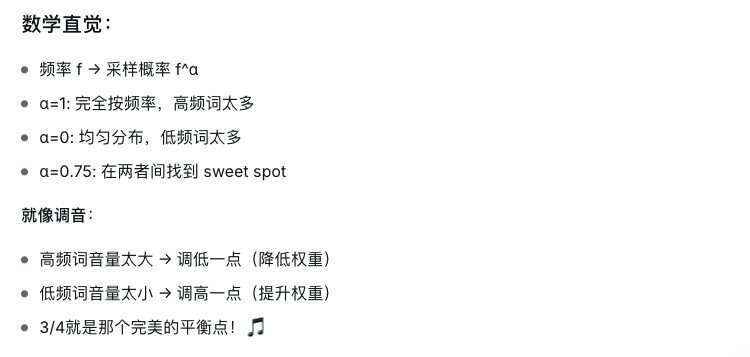
效果：
• 均匀采样：低频词被过度采样，高频词欠采样
• 按频率：高频词 dominate，"the"占10%，学习不平衡
• 3/4次幂：平衡！降低高频词权重，提升低频词机会

至于为什么是3/4？哈哈哈哈哈哈哈，笑死，数学直觉。

代码实现：

python 复制代码

import torch
import numpy as np

class NegativeSampler:
    def __init__(self, word_frequencies, num_negatives=5, power=0.75):
        """
        word_frequencies: 词频列表，长度=词汇表大小
        power: 幂次，通常0.75
        """
        self.vocab_size = len(word_frequencies)
        self.num_negatives = num_negatives
        
        # 1. 计算采样概率
        frequencies = np.array(word_frequencies, dtype=np.float32)
        
        # 2. 应用3/4次幂（核心！）
        probs = np.power(frequencies, power)
        
        # 3. 归一化
        probs = probs / probs.sum()
        
        # 4. 构建采样器
        self.probs = probs
        self.sampler = torch.distributions.Categorical(
            torch.from_numpy(probs)
        )
    
    def sample(self, center_word_idx, batch_size):
        """
        采样负样本，排除中心词本身
        center_word_idx: [batch_size] 中心词索引
        """
        negative_samples = []
        
        for _ in range(self.num_negatives):
            # 采样一批负样本
            samples = self.sampler.sample((batch_size,))  # [batch_size]
            
            # 排除中心词本身（重要！）
            # 如果采到了中心词，重新采样直到不是中心词
            for i in range(batch_size):
                while samples[i] == center_word_idx[i]:
                    samples[i] = self.sampler.sample()
            
            negative_samples.append(samples)
        
        # 组合成 [batch_size, num_negatives]
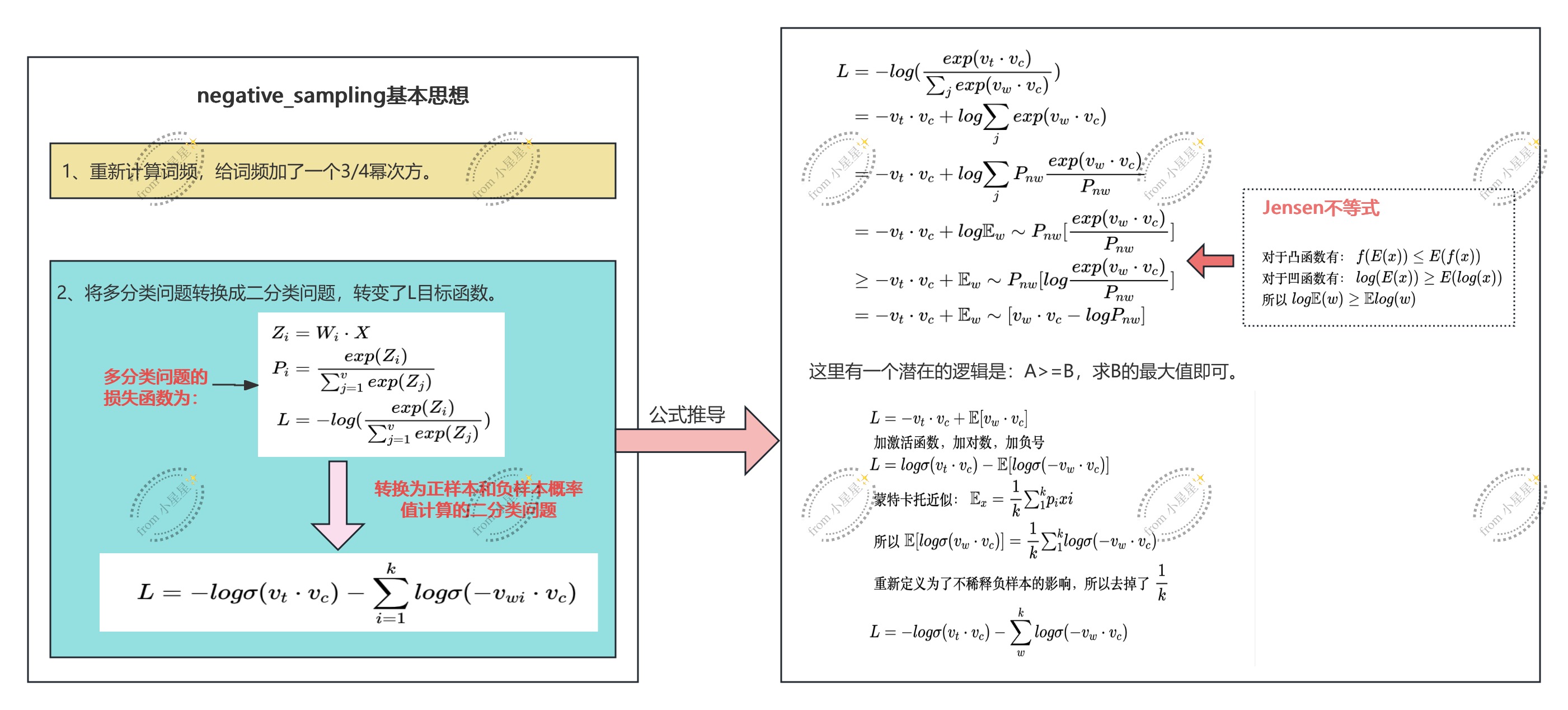
        return torch.stack(negative_samples, dim=1)

神来之笔：将多分类问题转变为二分类问题

传统的softmax：多分类（V选1）

负采样：二分类（是否是正样本？是/否）

具体策略：改变目标函数，对于一对(context,target)

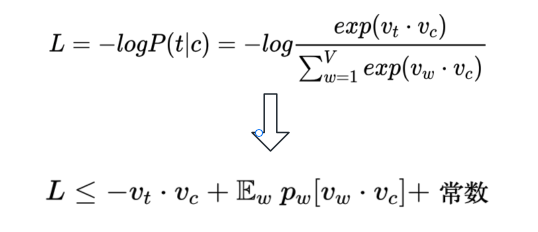
具体的公式推导如下：

高能的部分要来了哈，注意力要集中！

由于我们想要像E(x)= 累加Pi*Xi这个公式靠近，于是，就在log后面的加和函数上乘以一个P(w)，并处以一个P(w)：

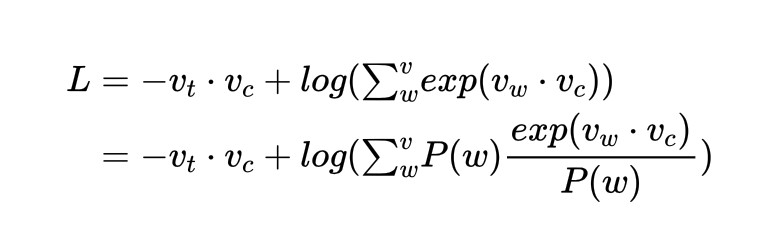
这个时候就会发生神奇的事情，我们会发现加和后面的式子在像期望函数靠近，即：

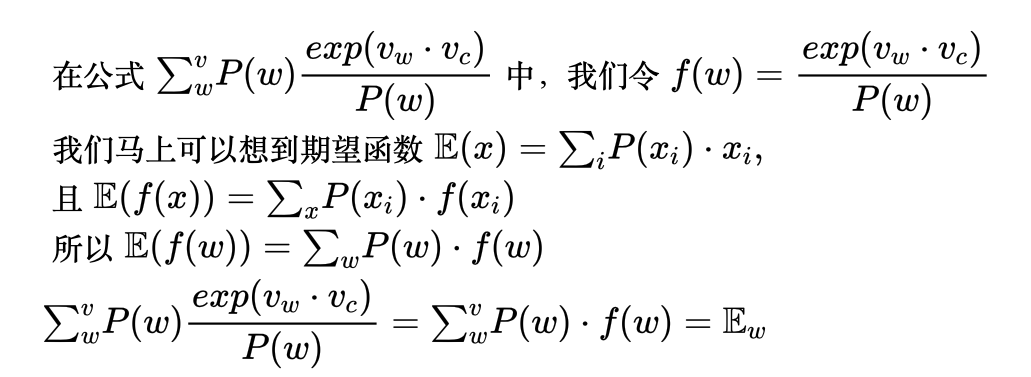
所以，我们最终得到一个推导结果：

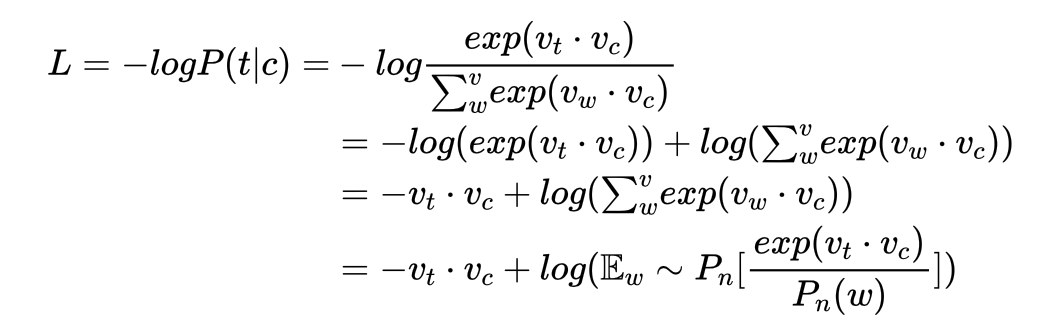
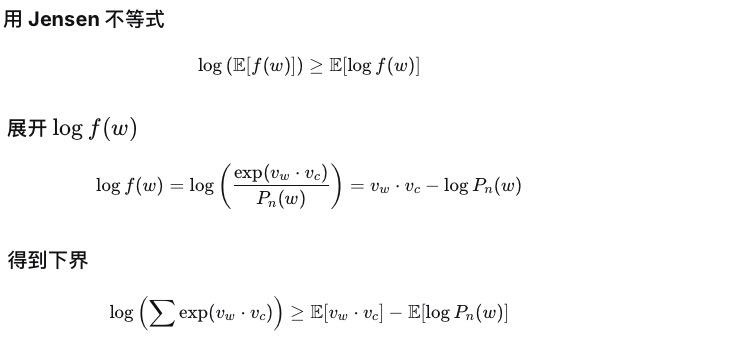
完整的推导链条是：

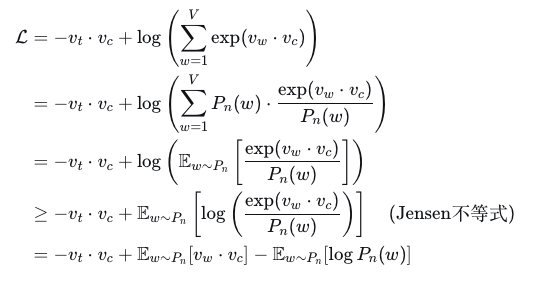
注意：Jensen不等式提供了一个下界，认为A>=B，那么求得B的最大值C之后也满足A>=C的不等式，此时我们就可以将求解B的最大值作为目标。此时，我们知道E～Pn[log Pn(w)]是一个常数值，不影响梯度计算，因此不作为影响因素纳入计算范围。

但是此时的Lbound下界是一个得分，但我们最终要计算的是一个概率，那就需要给这个L得分套上一个sigmoid激活函数，再取对数值，起到一个放大差异的作用，最终我们需要有一个可收敛的目标，即给概率值加一个负号，由此可以得到0是我们最终要靠近的目标值。即：

最终得到我们要求解的L，对L求导得到的参数就是我们需要的参数矩阵。那么可以继续思考一下，时间复杂度是如何减少的？对于L来说，计算L，对于一对(vt，vc)来说，需要计算b次点积(b是词向量的特征个数：n-dim)，复杂度为O(b)，对于一对(vt，vc)来说，需要计算k个负样本的概率值，也就是计算k次，总时间复杂度为O(kd)--->O(1)。所以负样本将时间复杂度降至了最低成本。