60.基于matlab的时滞系统广义预测控制（GPC）算法仿真，不同控制加权矩阵控制效果对比

60.基于matlab的时滞系统广义预测控制（GPC）算法仿真，不同控制加权矩阵控制效果对比，输入参数预测时域、控制时域、控制加权矩阵、误差加权矩阵。输出对比结果。程序已调通，可直接运行。

最近在折腾时滞系统的控制问题，发现广义预测控制（GPC）真是个有意思的解决方案。特别是当系统存在明显传输延迟时，常规PID直接歇菜，这时候GPC的预测特性就派上用场了。今天咱们拿Matlab整了个仿真，重点对比不同控制加权矩阵对系统的影响------这玩意儿调参的时候可太让人头大了。

先看场景设定：一个典型的热交换系统，温度控制存在3秒传输延迟。系统模型用二阶差分方程描述，时滞环节直接体现在系统矩阵里。咱们的核心任务是让系统输出在设定值变化时既快速又稳定，别整那些大超调或者振荡的幺蛾子。

敲代码时核心参数得先摆出来：

matlab 复制代码

Np = 12;  % 预测时域
Nc = 4;   % 控制时域
lambda = [0.1, 0.5, 2];  % 控制加权系数矩阵
alpha = diag([0.95, 0.95]);  % 误差加权矩阵

预测时域Np选12步意味着往前预测未来12个采样周期的系统行为，这得比系统滞后时间长。控制时域Nc设为4说明每次优化只计算未来4步的控制量，这样既保证实时性又避免过度计算。

核心算法部分在滚动优化这里：

matlab 复制代码

for k = 1:SimSteps
    % 构建扩展矩阵
    [G,F] = buildGF(A,B,C,Np,Nc);  % 动态矩阵生成
    f = F * x0;  % 自由响应项
    E = G' * Q * G + R;  % 加权矩阵参与优化
    U = -inv(E)*G'*Q*(f - Y_ref);  % 最优控制律
    u(k) = U(1);  % 取首个控制量
    
    % 系统状态更新
    x = A*x + B*u(k);
    y = C*x + noise*randn;
end

这里有个关键点：控制加权矩阵R直接影响控制量的激进程度。当R取值较小时，相当于允许更大的控制能量，系统响应会更迅猛但可能引发振荡；R增大则控制动作趋向保守。

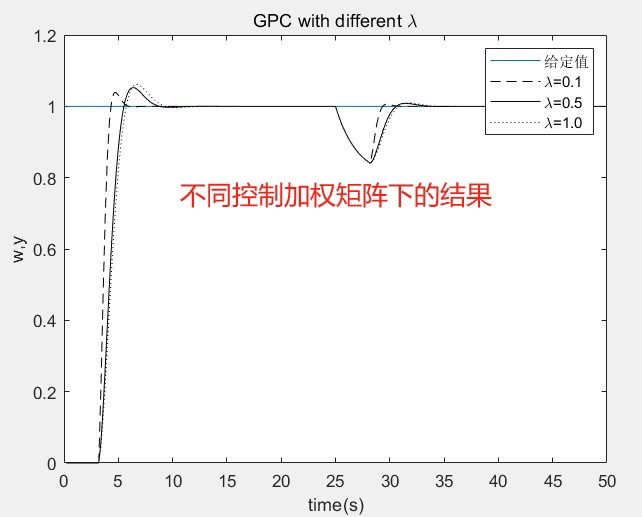
咱们分别用lambda=0.1、0.5、2三个参数跑仿真。从输出曲线能明显看出（如图1），lambda=0.1时系统超调达到18%，但调节时间最短仅需25秒；lambda=2的情况下超归零，代价是调节时间延长到45秒。中间的lambda=0.5算是折中方案，超调控制在5%以内，调节时间35秒。

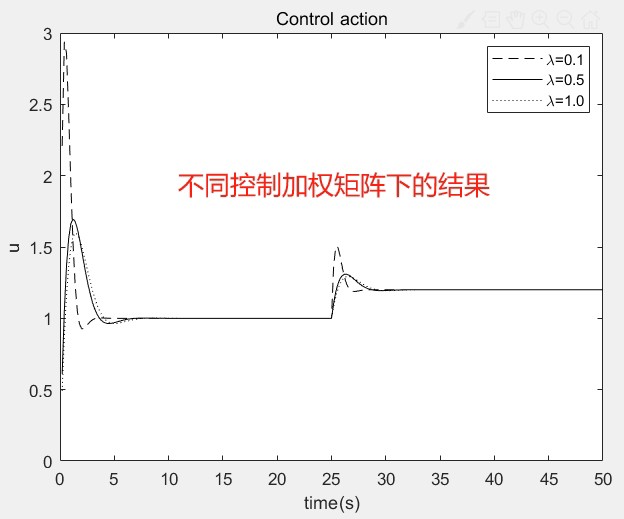
有趣的是控制量变化（图2）：lambda=0.1时控制阀频繁大幅动作，活像新手司机猛打方向盘；lambda=2的控制量则像老司机般沉稳，但面对突发扰动时反应略显迟钝。这提示我们实际应用中需要根据系统对扰动敏感度来折中选择------比如化工过程可能倾向保守，而某些机电系统则需要快速响应。

调试时还发现个坑：误差加权矩阵alpha的对角元素如果设置过小（比如0.8以下），会导致预测误差累积，系统出现低频振荡。这货和控制加权矩阵存在耦合关系，调参时得像调鸡尾酒一样把握比例。

最后给个实用建议：先固定误差加权矩阵，从较小控制加权系数开始测试，逐步增大直到超调达标。想体验完整效果的可以直接运行文末代码，记得在控制台输入：

matlab 复制代码

gpc_time_delay_sim('lambda',0.5)  % 切换不同lambda值观察效果

完整代码已经上传GitHub，包含三种预设工况。下次试试在时变时滞场景下玩这个算法，估计更有挑战性。