深度学习的链式法则

一、链式法则在深度学习里到底在干嘛？

最核心一句话：

深度学习训练 = 通过链式法则，把损失函数对每一层参数的导数算出来，然后用梯度下降更新参数。

数学上最经典的链式法则：

在深度学习中，经常是：

𝐿

L：损失函数（loss）

这就是反向传播里每一层算梯度的本质。

二、从一个最简单的标量例子开始

比如有：

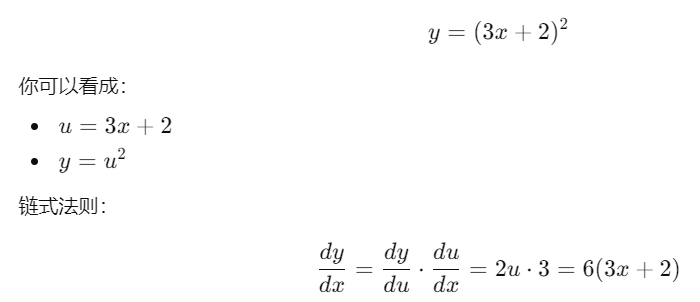
在代码里（伪反向传播）就是：

python 复制代码

x -> u = 3*x + 2 -> y = u**2
# 反向：
dy_du = 2 * u
du_dx = 3
dy_dx = dy_du * du_dx

神经网络只不过是这个过程的「多层版本」+「矩阵形式」。

三、一个两层全连接网络里的链式法则

设一个简单网络：

我们要：

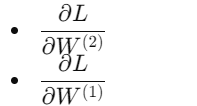
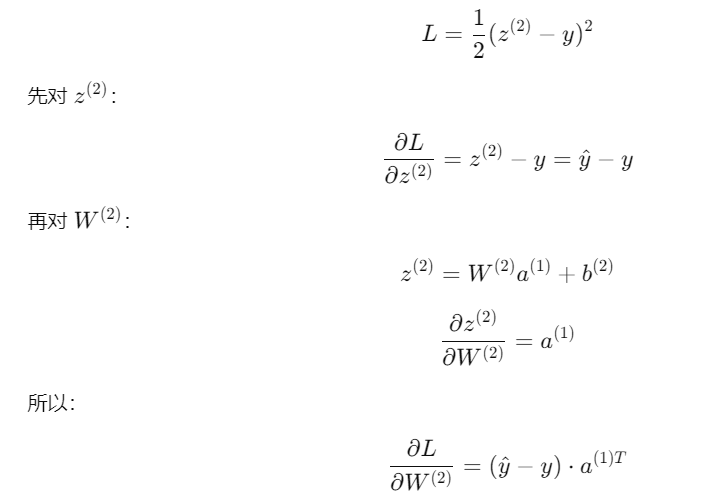
这整个过程，就是链式法则在神经网络里的「矩阵版」。

四、用纯 NumPy 手写一个小网络 + 反向传播

下面是一个1 隐层网络，只有一个样本时的前向、反向计算示例：

python 复制代码

import numpy as np

# 激活函数和导数（这里用 sigmoid）
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_grad(x):
    s = sigmoid(x)
    return s * (s - 1)

# 一些简单数据
np.random.seed(0)
x = np.random.randn(3, 1)     # 输入维度 3，列向量
y = np.array([[1.0]])         # 标量目标

# 网络结构：3 -> 4 -> 1
W1 = np.random.randn(4, 3)    # 第一层权重
b1 = np.zeros((4, 1))
W2 = np.random.randn(1, 4)    # 第二层权重
b2 = np.zeros((1, 1))

# ========= 前向传播 =========
# 隐藏层
z1 = W1 @ x + b1         # (4,1)
a1 = sigmoid(z1)         # (4,1)

# 输出层（线性）
z2 = W2 @ a1 + b2        # (1,1)
y_hat = z2               # 回归问题，输出=线性

# MSE 损失: 0.5 * (y_hat - y)^2
L = 0.5 * (y_hat - y) ** 2
print("Loss:", float(L))

# ========= 反向传播（链式法则） =========
# dL/dy_hat
dL_dyhat = (y_hat - y)   # (1,1)

# 输出层: y_hat = z2
dL_dz2 = dL_dyhat        # (1,1)

# dL/dW2 = dL/dz2 * da1/dW2 = dL/dz2 * a1^T
dL_dW2 = dL_dz2 @ a1.T   # (1,4)
dL_db2 = dL_dz2          # (1,1)

# 反传到 a1: dL/da1 = W2^T * dL/dz2
dL_da1 = W2.T @ dL_dz2   # (4,1)

# 过激活： a1 = sigmoid(z1)
dL_dz1 = dL_da1 * sigmoid_grad(z1)  # (4,1)

# 第一层参数
dL_dW1 = dL_dz1 @ x.T    # (4,3)
dL_db1 = dL_dz1          # (4,1)

print("dL_dW2 shape:", dL_dW2.shape)
print("dL_dW1 shape:", dL_dW1.shape)

可以在这段代码基础上：

加一个学习率 lr，用

W1 -= lr * dL_dW1 这样更新参数

循环多轮，就变成一个最简易的「手写版训练过程」。

五、用 PyTorch 看看自动求导怎么用链式法则

在 PyTorch 里你不会手写链式法则，但底层一样在做这件事。你只负责：

定义前向计算

调 loss.backward()

框架帮你自动用链式法则算梯度。

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim

# 简单两层网络
class SimpleNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(3, 4)
        self.act = nn.Sigmoid()
        self.fc2 = nn.Linear(4, 1)

    def forward(self, x):
        x = self.fc1(x)
        x = self.act(x)
        x = self.fc2(x)
        return x

net = SimpleNet()
criterion = nn.MSELoss()
optimizer = optim.SGD(net.parameters(), lr=0.1)

x = torch.randn(1, 3)   # batch=1, dim=3
y = torch.tensor([[1.0]])

# 前向
y_hat = net(x)
loss = criterion(y_hat, y)
print("loss:", loss.item())

# 反向（内部自动用链式法则）
optimizer.zero_grad()
loss.backward()

# 看梯度
for name, param in net.named_parameters():
    print(name, param.grad.shape)

你看到的 .grad 就是通过链式法则 + 计算图一层层传回来的结果。

总结一句

链式法则 = 把复杂复合函数的导数拆成一层一层的乘积

深度学习 = 用链式法则，把损失函数对每一层参数的梯度都算出来