2019-基于遗传算法的二维最大熵多阈值图像分割

1 论文简介

在图像分割领域，基于遗传算法的二维最大熵阈值分割论文已发表几十篇，知网最近可追溯到的是余荣泉和段先华在《计算机与数字工程》期刊上发表的《基于最大熵和遗传算法的图像分割方法研究》。该论文针对图像分割中传统最大熵阈值法存在的算法复杂度高、计算多阈值时运算时间长、对目标细节分割模糊以及分割结果不精确等问题，提出了将最大熵阈值分割法与遗传算法相结合的核心方法。该方法利用遗传算法的并行性、鲁棒性和自适应性，通过选择、交叉和变异操作快速搜索图像分割的最佳阈值，分别讨论了一维和二维最大熵阈值分割的情况，并以二维熵函数作为适应度函数优化阈值选择过程。该方法被广泛应用于图像处理、计算机视觉等领域，实验结果表明，与传统最大熵分割算法相比，该方法在分割效率和精度上均有显著提升，分割时间大幅缩短，细节分割效果更优，具有较高的理论价值和实践影响力。

2 算法原理

设原始图像 f(x,y)f(x, y)f(x,y) 大小为 M×NM \times NM×N，灰度级为 LLL，灰度均值对的概率为 Pij=nij/(M×N)P_{ij} = n_{ij} / (M \times N)Pij=nij/(M×N)，其中 nijn_{ij}nij 表示点灰度值为 iii、区域灰度均值为 jjj 的像素对个数。二维熵定义为：
H=−∑i=0L−1∑j=0L−1Pijlog⁡PijH = -\sum_{i=0}^{L-1} \sum_{j=0}^{L-1} P_{ij} \log P_{ij}H=−i=0∑L−1j=0∑L−1PijlogPij

阈值 (s,t)(s, t)(s,t) 将图像分为目标区 AAA 和背景区 BBB，目标区概率为：
PA=∑i=0s∑j=0tPijP_A = \sum_{i=0}^{s} \sum_{j=0}^{t} P_{ij}PA=i=0∑sj=0∑tPij

背景区概率为：
PB=∑i=s+1L−1∑j=t+1L−1PijP_B = \sum_{i=s+1}^{L-1} \sum_{j=t+1}^{L-1} P_{ij}PB=i=s+1∑L−1j=t+1∑L−1Pij

目标区熵为：
H(A)=−∑i=0s∑j=0tPijPAlog⁡PijPA=log⁡PA+HAPAH(A) = -\sum_{i=0}^{s} \sum_{j=0}^{t} \frac{P_{ij}}{P_A} \log \frac{P_{ij}}{P_A} = \log P_A + \frac{H_A}{P_A}H(A)=−i=0∑sj=0∑tPAPijlogPAPij=logPA+PAHA

其中 HA=−∑i=0s∑j=0tPijlog⁡PijH_A = -\sum_{i=0}^{s} \sum_{j=0}^{t} P_{ij} \log P_{ij}HA=−∑i=0s∑j=0tPijlogPij。

背景区熵为：
H(B)=−∑i=s+1L−1∑j=t+1L−1PijPBlog⁡PijPB=log⁡PB+HBPBH(B) = -\sum_{i=s+1}^{L-1} \sum_{j=t+1}^{L-1} \frac{P_{ij}}{P_B} \log \frac{P_{ij}}{P_B} = \log P_B + \frac{H_B}{P_B}H(B)=−i=s+1∑L−1j=t+1∑L−1PBPijlogPBPij=logPB+PBHB

其中 HB=−∑i=s+1L−1∑j=t+1L−1Pijlog⁡PijH_B = -\sum_{i=s+1}^{L-1} \sum_{j=t+1}^{L-1} P_{ij} \log P_{ij}HB=−∑i=s+1L−1∑j=t+1L−1PijlogPij。

假设边界和噪声区概率可忽略，则 PB=1−PAP_B = 1 - P_APB=1−PA，HB=HL−HAH_B = H_L - H_AHB=HL−HA，其中 HL=−∑i=0L−1∑j=0L−1Pijlog⁡PijH_L = -\sum_{i=0}^{L-1} \sum_{j=0}^{L-1} P_{ij} \log P_{ij}HL=−∑i=0L−1∑j=0L−1PijlogPij。判别函数为：
φ(s,t)=H(A)+H(B)=log⁡[PA(1−PA)]+HAPA+HL−HA1−PA\varphi(s, t) = H(A) + H(B) = \log [P_A (1-P_A)] + \frac{H_A}{P_A} + \frac{H_L - H_A}{1-P_A}φ(s,t)=H(A)+H(B)=log[PA(1−PA)]+PAHA+1−PAHL−HA

最佳阈值通过 (s∗,t∗)=arg⁡max⁡φ(s,t)(s^*, t^*) = \arg \max \varphi(s, t)(s∗,t∗)=argmaxφ(s,t) 确定。基于最大熵和遗传算法的图像分割方法将遗传算法应用于阈值搜索过程。具体步骤如下：

Step1：随机产生初始种群，设置初始代数 Gen 为 0。
Step2：采用 16 位二进制编码对染色体进行编码，每个染色体代表一个分割阈值。
Step3：设定种群规模为 50，最大繁殖代数为 100。
Step4：解码染色体为 [0,255][0, 255][0,255] 范围内的值，以二维熵函数 φ(s,t)\varphi(s, t)φ(s,t) 作为适应度函数计算个体适应度。
Step5：使用轮盘赌方法进行选择操作，计算个体相对适应度并确定选中次数。
Step6：采用单点交叉操作，交叉概率设置为 0.8。
Step7：采用基本变异操作，变异概率设置为 0.1。
Step8：判断终止条件，当达到最大代数 50 或群体最高适应度值不再变化时终止算法，否则重复 Step4 至 Step7。
Step9：将最高适应度值对应的阈值用于图像分割。

3 实验结果

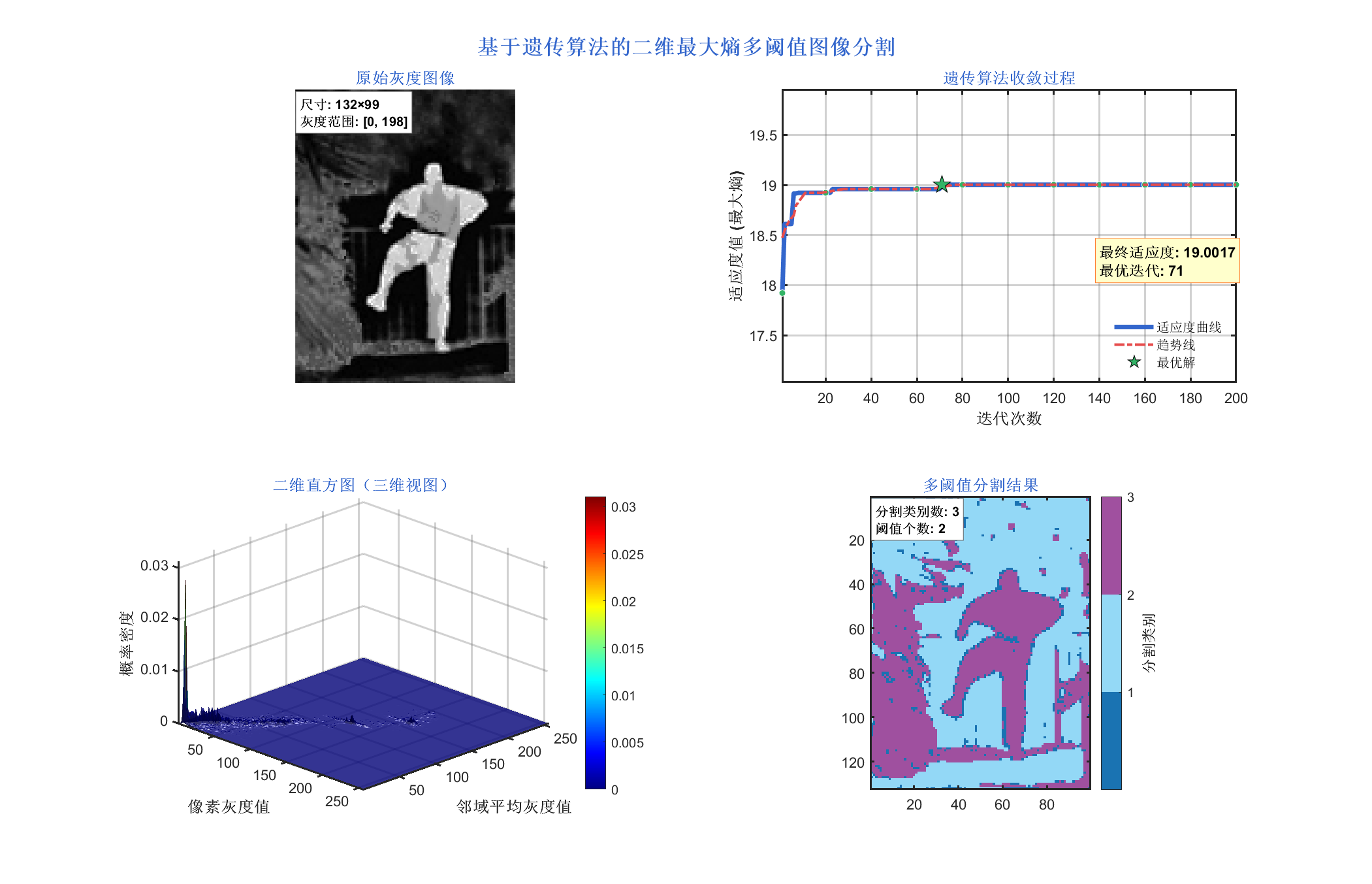
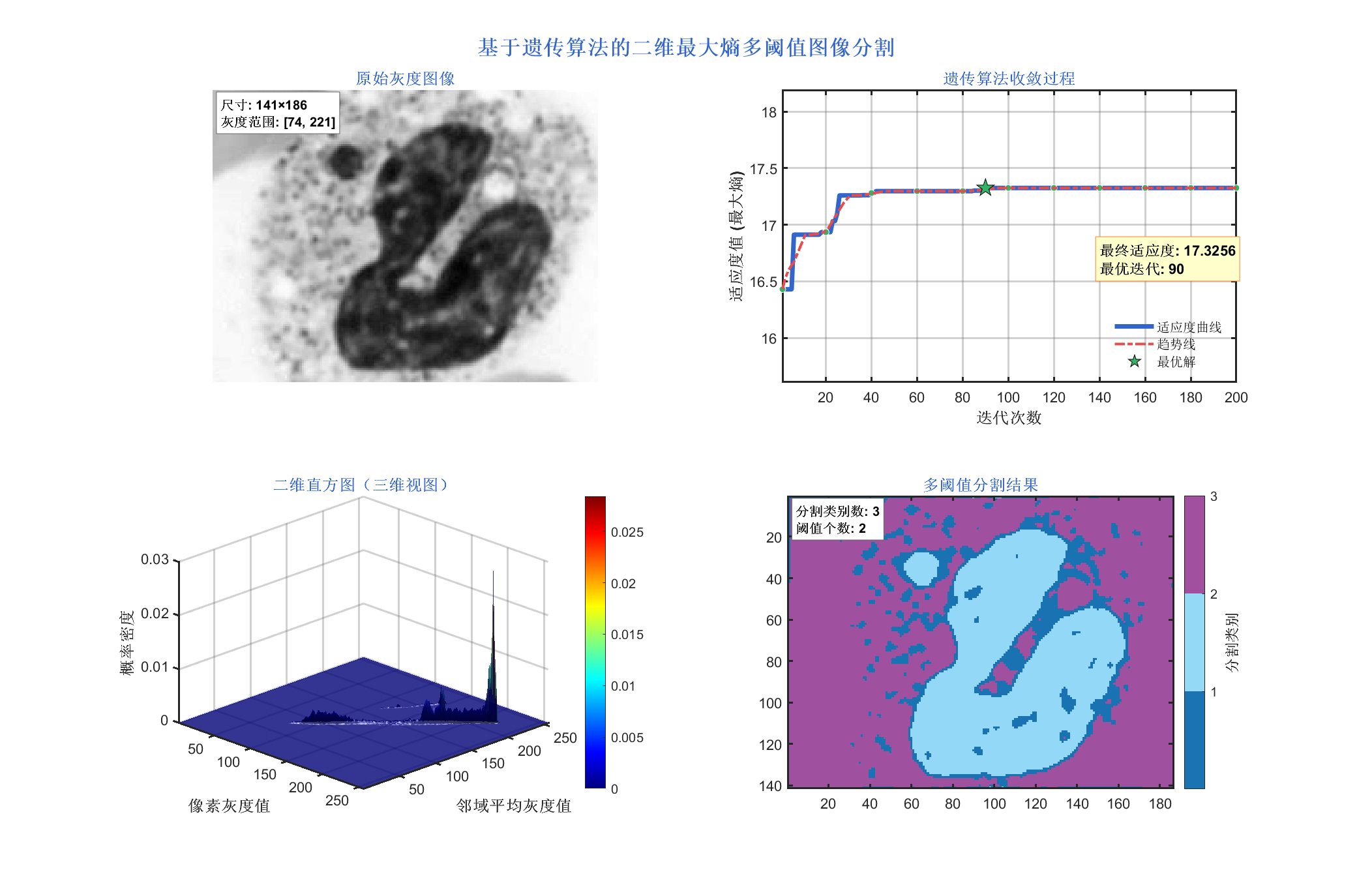
4 参考文献

1\] 陆新泉, 李宁, 陈世福, 等. 基于二维阈值化和遗传算法的图像分割方法\[J\]. 计算机应用与软件, 2001, (12):57-59+65. \[2\] 陈果, 左洪福. 图像分割的二维最大熵遗传算法\[J\]. 计算机辅助设计与图形学学报, 2002, (06):530-534. \[3\] 吴薇, 赵旭, 邓秋霞. 基于遗传算法的二维最大熵图像分割算法\[J\]. 武警工程学院学报, 2003, (04):25-27. \[4\] 练玉来, 耿军雪. 遗传算法在二维熵图像分割中的应用\[J\]. 现代电子技术, 2004, (15):25-27+30. \[5\] 张红蕾, 宋建社, 翟晓颖. 一种基于二维最大熵的 SAR 图像自适应阈值分割算法\[J\]. 电光与控制, 2007, (04):63-65+69. \[6\] 欧萍, 贺电. 遗传算法粒在二维最大熵值图像分割中的应用\[J\]. 计算机仿真, 2011, 28(01):294-297+343. \[7\] 余荣泉, 段先华. 基于最大熵和遗传算法的图像分割方法研究\[J\]. 计算机与数字工程, 2019, 47(07):1805-1809. ## 5 MATLAB 代码