PyTorch 实现 BP 神经网络：从函数拟合到分类任务

引言

反向传播（Back Propagation，BP）神经网络是深度学习的基础，通过前向传播计算输出，反向传播更新权重，能够有效学习非线性映射关系。本文将通过两个经典实验，详细介绍如何使用 PyTorch 实现 BP 神经网络：一维函数拟合 和鸢尾花分类，涵盖数据准备、网络构建、模型训练、结果可视化等完整流程。

一、BP 神经网络理论基础

1. 网络结构

BP 神经网络通常包含输入层、隐藏层和输出层：

输入层：接收原始数据
隐藏层：提取特征，层数和神经元数量决定网络复杂度
输出层：产生最终结果，回归任务用线性激活，分类任务用 Softmax

2. 核心算法

前向传播 ：从输入到输出逐层计算，公式为
反向传播 ：根据损失函数 L，使用链式法则计算梯度，更新权重
激活函数：常用 tanh、ReLU 等，引入非线性能力
损失函数：回归用 MSE，分类用 CrossEntropy
优化器：如 Adam、SGD，加速收敛

二、实验一：一维函数拟合

1. 数据准备

使用表 5-1 中的一维数据，共 21 个样本，输入，目标输出 D 为非线性函数值：

python 复制代码

X = [-1.0, -0.9, ..., 1.0]  # 21个输入点
D = [-0.9602, -0.5770, ..., -0.3201]  # 对应目标输出

2. 网络结构设计

构建 1-10-1 的三层 BP 网络，隐藏层和输出层均使用 tanh 激活：

python 复制代码

class BPNetwork(nn.Module):
    def __init__(self):
        super(BPNetwork, self).__init__()
        self.hidden_layer = nn.Linear(1, 10)  # 输入→隐藏
        self.output_layer = nn.Linear(10, 1)   # 隐藏→输出

    def forward(self, x):
        hidden_out = torch.tanh(self.hidden_layer(x))  # tansig激活
        output_out = torch.tanh(self.output_layer(hidden_out))
        return output_out

3. 训练参数设置

损失函数：均方误差（MSE）
优化器：Adam，学习率 0.01
最大迭代：1000 轮，目标损失 0.005

4. 训练过程

python 复制代码

for epoch in range(max_epochs):
    O_tensor = net(X_tensor)  # 前向传播
    loss = criterion(O_tensor, D_tensor)  # 计算损失
    optimizer.zero_grad()  # 梯度清零
    loss.backward()  # 反向传播
    optimizer.step()  # 更新参数

5. 结果可视化

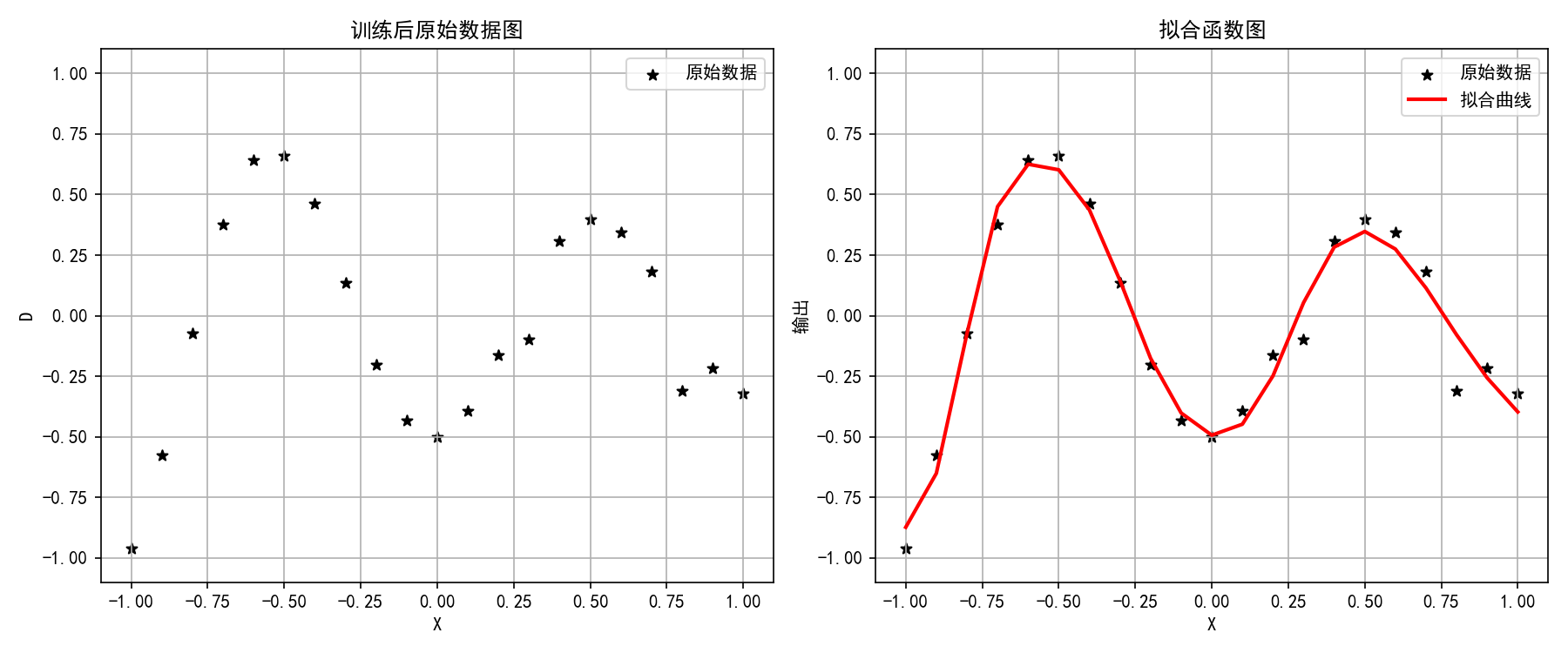
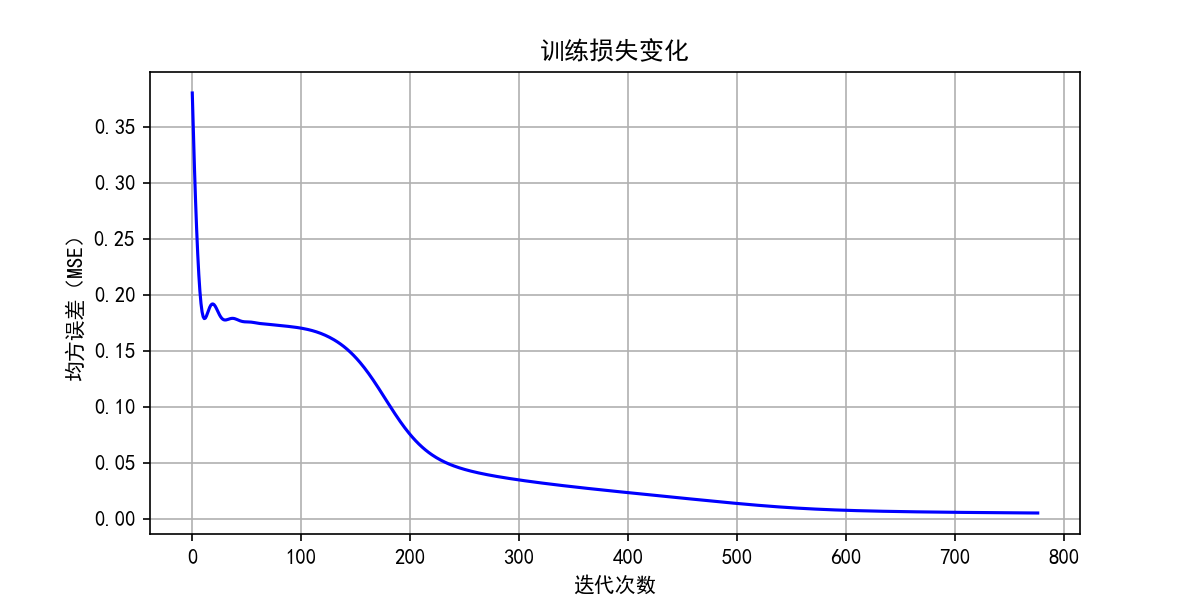
拟合效果：红色曲线为网络输出，黑色星号为原始数据
损失曲线：蓝色曲线展示损失随迭代次数的下降过程

三、实验二：鸢尾花分类

1. 数据集介绍

鸢尾花数据集包含 150 个样本，4 个特征（花萼长度、宽度，花瓣长度、宽度），3 个类别（山鸢尾、变色鸢尾、维吉尼亚鸢尾）。

2. 数据预处理

划分数据集：80% 训练集，20% 测试集，分层抽样保持类别平衡
归一化：使用 MinMaxScaler 将特征缩放到 [0,1] 区间

python 复制代码

x_train0, x_test0, y_train, y_test = train_test_split(
    iris.data, iris.target, test_size=0.2, random_state=22, stratify=iris.target
)
min_max_scaler = preprocessing.MinMaxScaler()
x_train = min_max_scaler.fit_transform(x_train0)
x_test = min_max_scaler.transform(x_test0)

3. 网络结构设计

构建 4-20-3 的三层 BP 网络，隐藏层用 ReLU 激活，输出层用 Softmax：

python 复制代码

class BPNetModel(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(BPNetModel, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        self.out = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        x = Fun.relu(self.hidden(x))  # ReLU激活
        out = Fun.softmax(self.out(x), dim=1)  # Softmax输出概率
        return out

4. 训练参数设置

学习率：0.02
迭代次数：300 轮
隐藏层神经元：20
优化器：Adam
损失函数：交叉熵

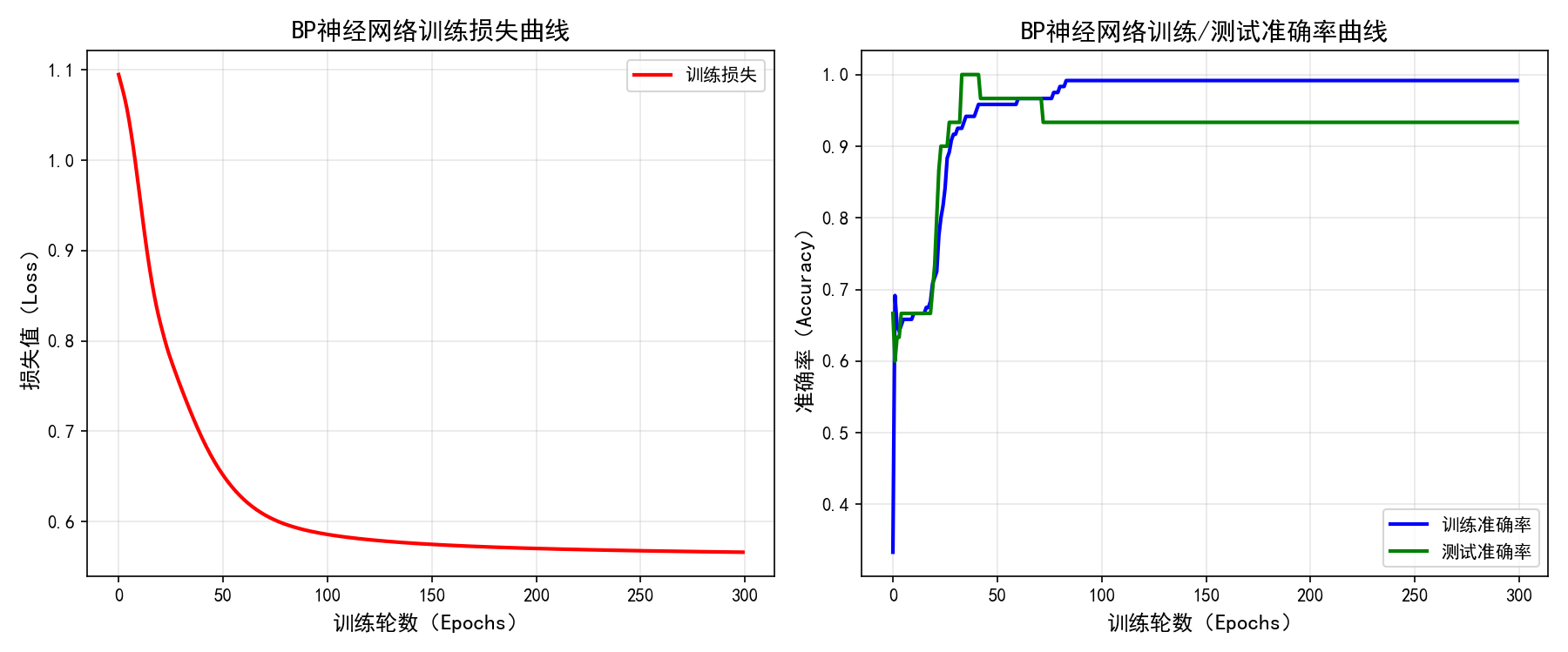
5. 训练过程可视化

损失曲线：红色曲线展示训练损失随迭代的下降
准确率曲线：蓝色（训练集）和绿色（测试集）曲线展示准确率变化

6. 分类结果评估

分类报告：包含精确率、召回率、F1 分数
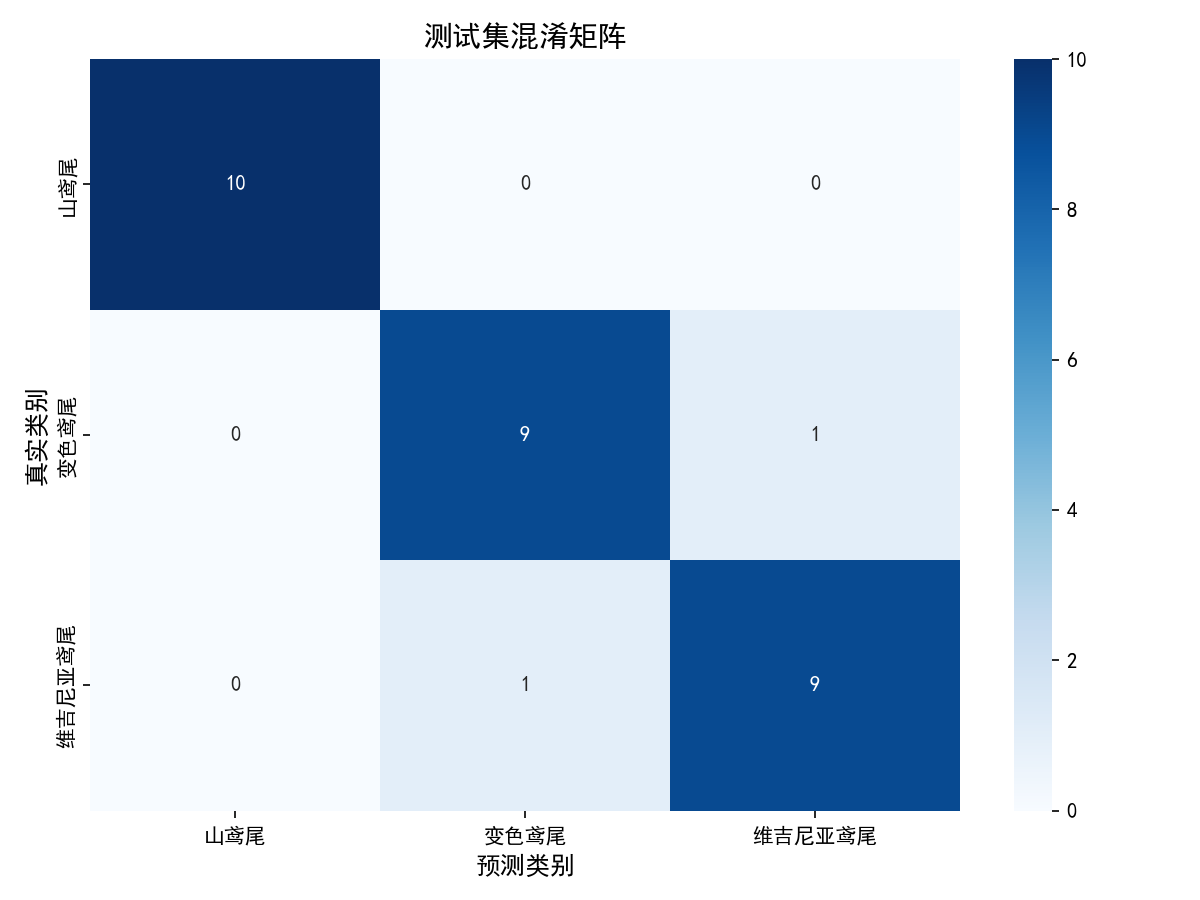
混淆矩阵：热力图展示分类结果的混淆情况
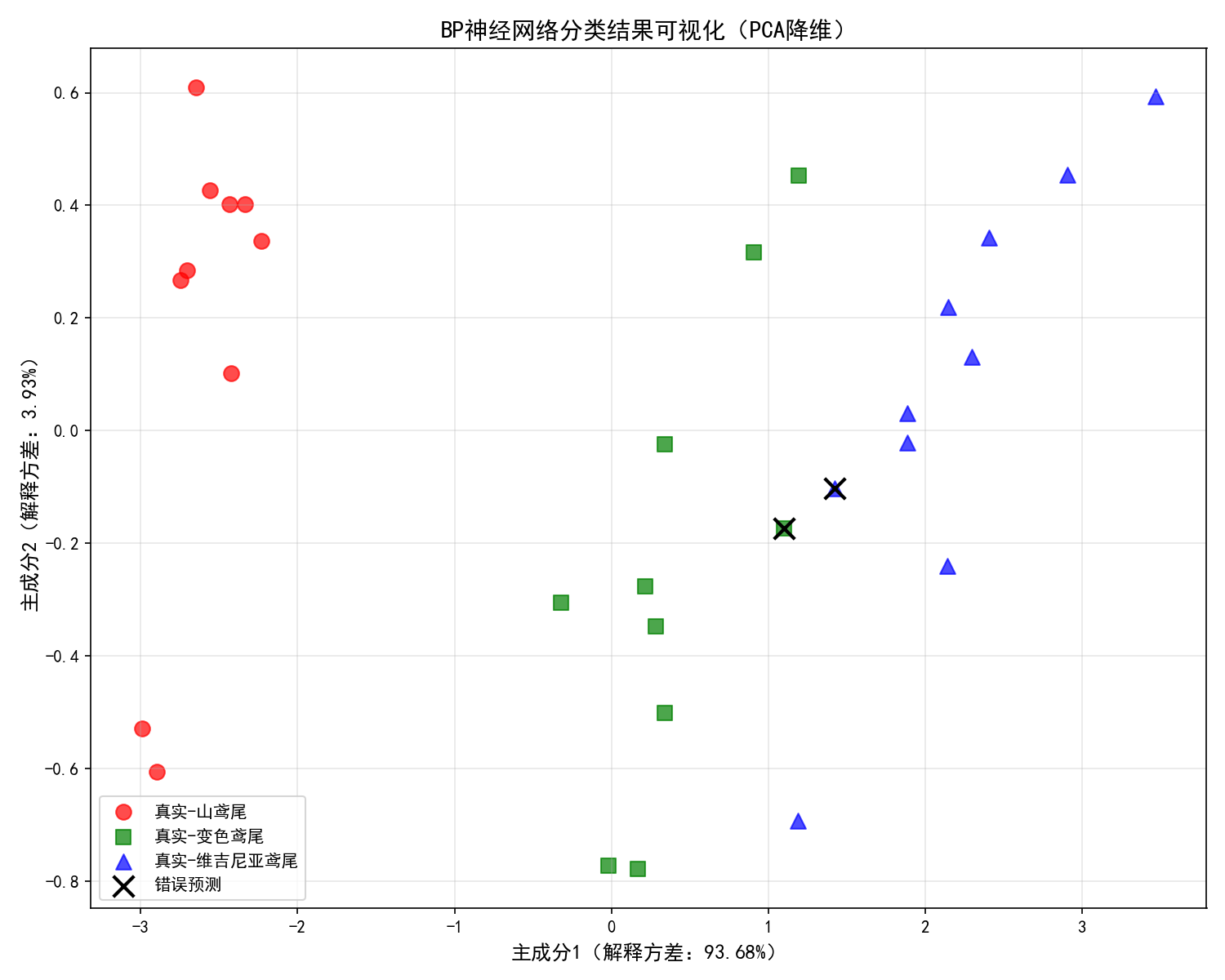
PCA 可视化：将 4 维特征降维到 2 维，直观展示分类效果

分类报告

python 复制代码

              precision    recall  f1-score   support

         山鸢尾     1.0000    1.0000    1.0000        10
        变色鸢尾     0.9000    0.9000    0.9000        10
      维吉尼亚鸢尾     0.9000    0.9000    0.9000        10

    accuracy                         0.9333        30
   macro avg     0.9333    0.9333    0.9333        30
weighted avg     0.9333    0.9333    0.9333        30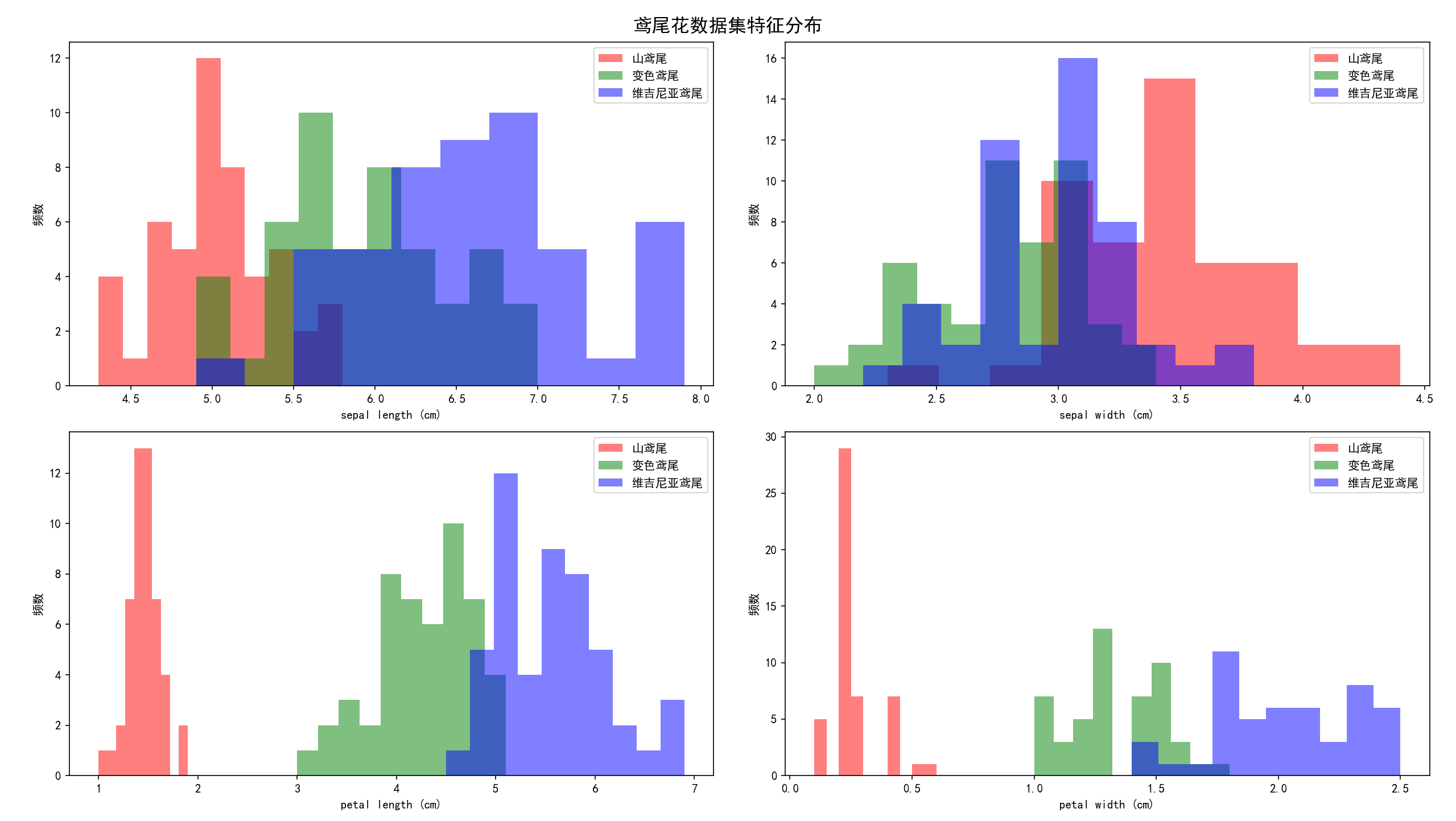

四、实验结果分析

1. 函数拟合实验

网络在第551轮收敛（1000轮以内每次训练可能不一样)，损失=0.004997，低于目标值 0.005
拟合曲线与原始数据高度重合，说明 BP 网络能够有效学习非线性函数关系
tanh 激活函数在回归任务中表现良好，输出范围 [-1,1] 与目标数据匹配

2. 鸢尾花分类实验

训练集准确率：0.9917，测试集准确率：0.9333，模型泛化能力良好
混淆矩阵显示仅 1 个变色鸢尾被误分类为维吉尼亚鸢尾
PCA 可视化直观展示了分类边界，错误预测点用黑色叉号标记
ReLU+Softmax 组合在分类任务中表现优异，加速了训练收敛

五、BP 神经网络的优缺点

优点

能够学习复杂的非线性映射关系
结构灵活，可通过调整层数和神经元数量适应不同任务
训练过程自动化，无需手动提取特征
广泛应用于回归、分类、聚类等多种任务

缺点

容易过拟合，需要正则化等技术
训练时间长，计算资源消耗大
初始权重敏感，需要合适的初始化方法
黑箱模型，可解释性差

六、完整代码

实验一：函数拟合

python 复制代码

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl

# 全局设置
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 数据准备
X = [-1.0, -0.9, -0.8, -0.7, -0.6, -0.5, -0.4, -0.3, -0.2, -0.1, 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
D = [-0.9602, -0.5770, -0.0729, 0.3771, 0.6405, 0.6600, 0.4609, 0.1336, -0.2013, -0.4344, -0.5000, -0.3930, -0.1647, -0.0988, 0.3072, 0.3960, 0.3449, 0.1816, -0.3120, -0.2189, -0.3201]
X_tensor = torch.tensor(X, dtype=torch.float32).view(-1, 1)
D_tensor = torch.tensor(D, dtype=torch.float32).view(-1, 1)

# 网络定义
class BPNetwork(nn.Module):
    def __init__(self):
        super(BPNetwork, self).__init__()
        self.hidden_layer = nn.Linear(1, 10)
        self.output_layer = nn.Linear(10, 1)

    def forward(self, x):
        hidden_out = torch.tanh(self.hidden_layer(x))
        output_out = torch.tanh(self.output_layer(hidden_out))
        return output_out

# 模型初始化
net = BPNetwork()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.01)

# 训练过程
max_epochs = 1000
target_loss = 0.005
loss_history = []

for epoch in range(max_epochs):
    O_tensor = net(X_tensor)
    loss = criterion(O_tensor, D_tensor)
    loss_history.append(loss.item())
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if loss.item() < target_loss:
        print(f"提前停止训练：第{epoch + 1}轮，损失={loss.item():.6f}")
        break

# 结果可视化
with torch.no_grad():
    O = net(X_tensor).numpy()

plt.figure(figsize=(12, 5))
plt.subplot(121)
plt.scatter(X, D, c='k', marker='*', label='原始数据')
plt.xlabel('X')
plt.ylabel('D')
plt.title('训练后原始数据图')
plt.xlim(-1.1, 1.1)
plt.ylim(-1.1, 1.1)
plt.grid(True)
plt.legend()

plt.subplot(122)
plt.scatter(X, D, c='k', marker='*', label='原始数据')
plt.plot(X, O, 'r-', linewidth=2, label='拟合曲线')
plt.xlabel('X')
plt.ylabel('输出')
plt.title('拟合函数图')
plt.xlim(-1.1, 1.1)
plt.ylim(-1.1, 1.1)
plt.grid(True)
plt.legend()

plt.tight_layout()
plt.show()

plt.figure(figsize=(8, 4))
plt.plot(range(len(loss_history)), loss_history, 'b-')
plt.xlabel('迭代次数')
plt.ylabel('均方误差（MSE）')
plt.title('训练损失变化')
plt.grid(True)
plt.show()

实验二：鸢尾花分类

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import datasets
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.decomposition import PCA  # 用于降维可视化
import seaborn as sns  # 用于绘制混淆矩阵
import torch
import torch.nn.functional as Fun

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 设置超参数
lr = 0.02
epochs = 300
n_feature = 4
n_hidden = 20
n_output = 3

# ====================== 1. 数据集展示 ======================
print("=" * 60)
print("  鸢尾花数据集展示")
print("=" * 60)

# 加载数据集
iris = datasets.load_iris()
# 转换为DataFrame方便展示
iris_df = pd.DataFrame(
    data=np.c_[iris.data, iris.target],
    columns=iris.feature_names + ['类别']
)

# 【关键修正】鸢尾花类别映射：0/1/2对应三个品种
iris_df['类别'] = iris_df['类别'].map({0: '山鸢尾', 1: '变色鸢尾', 2: '维吉尼亚鸢尾'})

# 1.1 数据集基本信息
print("\n1. 数据集基本信息：")
print(f"数据集样本总数：{len(iris.data)}")
print(f"特征数量：{iris.data.shape[1]}")
print(f"类别数量：{len(iris.target_names)}")
print(f"类别名称：{', '.join(iris.target_names)}")
print(f"特征名称：{', '.join(iris.feature_names)}")

# 1.2 数据集前5行
print("\n2. 数据集前5行：")
print(iris_df.head())

# 1.3 数据集统计描述
print("\n3. 数据集统计描述：")
print(iris_df.describe())

# 1.4 类别分布
print("\n4. 类别分布：")
class_count = iris_df['类别'].value_counts()
print(class_count)

# 1.5 特征分布可视化
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
fig.suptitle('鸢尾花数据集特征分布', fontsize=16, fontweight='bold')

features = iris.feature_names
for i, (ax, feature) in enumerate(zip(axes.flatten(), features)):
    for label, color, name in zip([0, 1, 2], ['red', 'green', 'blue'], ['山鸢尾', '变色鸢尾', '维吉尼亚鸢尾']):
        ax.hist(iris.data[iris.target == label, i], alpha=0.5, color=color, label=name)
    ax.set_xlabel(feature)
    ax.set_ylabel('频数')
    ax.legend()

plt.tight_layout()
plt.savefig('数据集特征分布.png', dpi=300, bbox_inches='tight')
plt.show()

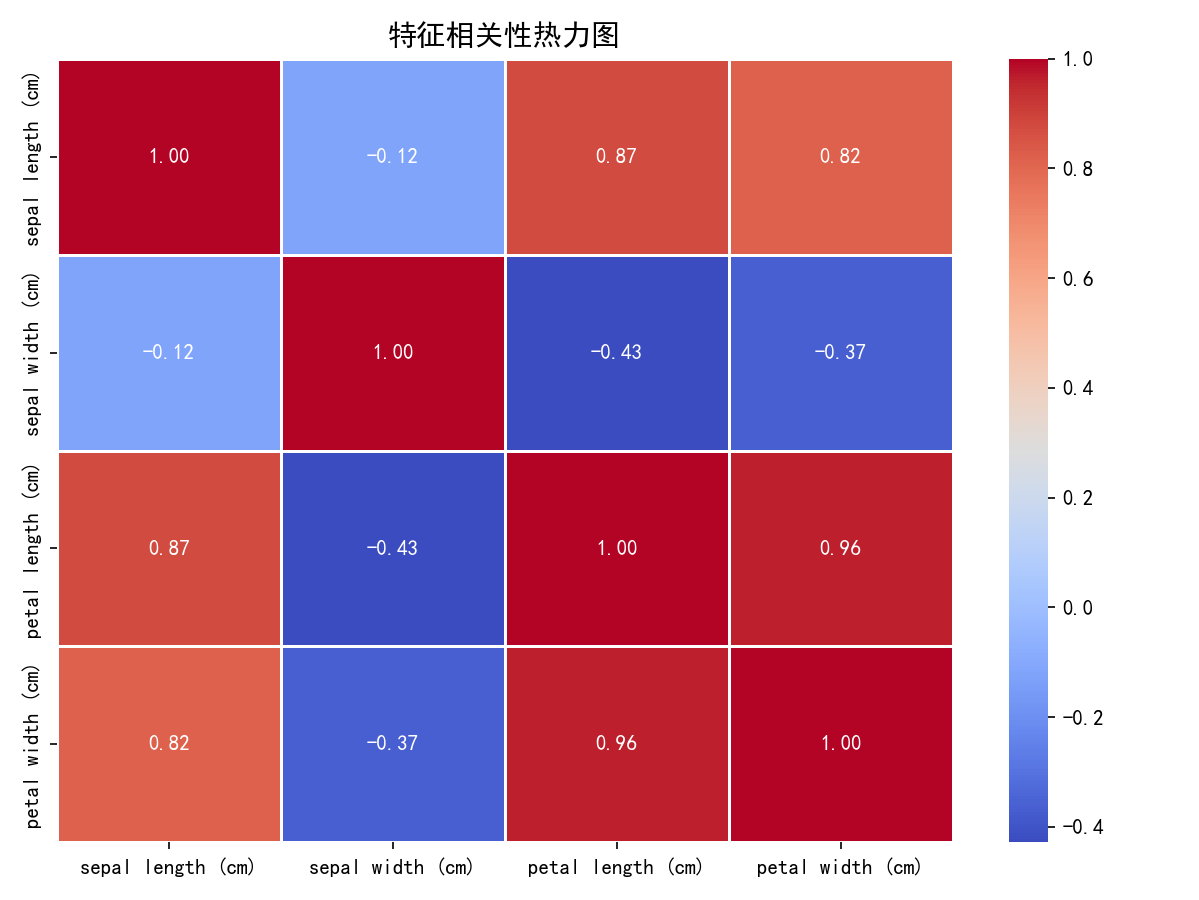
# 1.6 特征相关性热力图
print("\n5. 特征相关性矩阵：")
corr_matrix = pd.DataFrame(iris.data, columns=features).corr()
print(corr_matrix)

plt.figure(figsize=(8, 6))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt='.2f', linewidths=0.5)
plt.title('特征相关性热力图', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.savefig('特征相关性热力图.png', dpi=300, bbox_inches='tight')
plt.show()

print("=" * 60 + "\n")

# ====================== 2. 数据预处理 ======================
# 划分训练集和测试集
x_train0, x_test0, y_train, y_test = train_test_split(
    iris.data, iris.target, test_size=0.2, random_state=22, stratify=iris.target
)

# 归一化
min_max_scaler = preprocessing.MinMaxScaler()
x_train = min_max_scaler.fit_transform(x_train0)
x_test = min_max_scaler.transform(x_test0)  # 测试集只transform，不fit

# 转换为tensor
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)
x_test = torch.FloatTensor(x_test)
y_test = torch.LongTensor(y_test)


# ====================== 3. 定义BP神经网络 ======================
class BPNetModel(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(BPNetModel, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        self.out = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        x = Fun.relu(self.hidden(x))
        out = Fun.softmax(self.out(x), dim=1)
        return out


# 初始化网络、优化器和损失函数
net = BPNetModel(n_feature=n_feature, n_hidden=n_hidden, n_output=n_output)
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
loss_fun = torch.nn.CrossEntropyLoss()

# ====================== 4. 模型训练 ======================
print("开始模型训练...")
loss_steps = np.zeros(epochs)
train_accuracy_steps = np.zeros(epochs)  # 新增训练集准确率
test_accuracy_steps = np.zeros(epochs)

for epoch in range(epochs):
    # 训练模式
    net.train()
    y_pred_train = net(x_train)
    loss = loss_fun(y_pred_train, y_train)

    # 反向传播和优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # 保存损失值
    loss_steps[epoch] = loss.item()

    # 计算训练集准确率
    with torch.no_grad():
        train_correct = (torch.argmax(y_pred_train, dim=1) == y_train).type(torch.FloatTensor)
        train_accuracy_steps[epoch] = train_correct.mean().item()

    # 测试集评估
    net.eval()
    with torch.no_grad():
        y_pred_test = net(x_test)
        test_correct = (torch.argmax(y_pred_test, dim=1) == y_test).type(torch.FloatTensor)
        test_accuracy_steps[epoch] = test_correct.mean().item()

    # 每50轮打印一次信息
    if (epoch + 1) % 50 == 0:
        print(f"第{epoch + 1:3d}轮 | 训练损失：{loss.item():.4f} | "
              f"训练准确率：{train_accuracy_steps[epoch]:.4f} | "
              f"测试准确率：{test_accuracy_steps[epoch]:.4f}")

print("\n模型训练完成！")

# ====================== 5. 训练过程可视化（损失值曲线图） ======================
plt.figure(figsize=(12, 5))

# 损失值曲线
plt.subplot(1, 2, 1)
plt.plot(range(epochs), loss_steps, color='red', linewidth=2, label='训练损失')
plt.xlabel('训练轮数（Epochs）', fontsize=12)
plt.ylabel('损失值（Loss）', fontsize=12)
plt.title('BP神经网络训练损失曲线', fontsize=14, fontweight='bold')
plt.legend()
plt.grid(True, alpha=0.3)

# 准确率曲线
plt.subplot(1, 2, 2)
plt.plot(range(epochs), train_accuracy_steps, color='blue', linewidth=2, label='训练准确率')
plt.plot(range(epochs), test_accuracy_steps, color='green', linewidth=2, label='测试准确率')
plt.xlabel('训练轮数（Epochs）', fontsize=12)
plt.ylabel('准确率（Accuracy）', fontsize=12)
plt.title('BP神经网络训练/测试准确率曲线', fontsize=14, fontweight='bold')
plt.legend()
plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.savefig('训练过程可视化.png', dpi=300, bbox_inches='tight')
plt.show()

# ====================== 6. 分类结果展示 ======================
print("\n" + "=" * 60)
print("                      分类结果展示")
print("=" * 60)

# 生成最终预测结果
net.eval()
with torch.no_grad():
    y_pred_train_final = torch.argmax(net(x_train), dim=1).numpy()
    y_pred_test_final = torch.argmax(net(x_test), dim=1).numpy()
    y_train_np = y_train.numpy()
    y_test_np = y_test.numpy()

# 6.1 分类报告（精确率、召回率、F1分数）
print("\n1. 测试集分类报告：")
print(classification_report(
    y_test_np, y_pred_test_final,
    target_names=['山鸢尾', '变色鸢尾', '维吉尼亚鸢尾'],  # 中文类别名称
    digits=4
))

# 6.2 混淆矩阵可视化
cm = confusion_matrix(y_test_np, y_pred_test_final)
plt.figure(figsize=(8, 6))
sns.heatmap(
    cm, annot=True, fmt='d', cmap='Blues',
    xticklabels=['山鸢尾', '变色鸢尾', '维吉尼亚鸢尾'],
    yticklabels=['山鸢尾', '变色鸢尾', '维吉尼亚鸢尾']
)
plt.xlabel('预测类别', fontsize=12)
plt.ylabel('真实类别', fontsize=12)
plt.title('测试集混淆矩阵', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.savefig('混淆矩阵.png', dpi=300, bbox_inches='tight')
plt.show()

# 6.3 分类结果散点图（使用PCA降维到2D可视化）
print("\n2. 分类结果可视化（PCA降维）：")
# 对测试集特征进行PCA降维
pca = PCA(n_components=2)
x_test_pca = pca.fit_transform(x_test0)  # 使用原始测试集特征（未归一化）进行可视化

# 绘制散点图
plt.figure(figsize=(10, 8))
# 绘制标签
for label, color, marker, name in zip([0, 1, 2], ['red', 'green', 'blue'], ['o', 's', '^'], ['山鸢尾', '变色鸢尾', '维吉尼亚鸢尾']):
    mask = y_test_np == label
    plt.scatter(
        x_test_pca[mask, 0], x_test_pca[mask, 1],
        c=color, marker=marker, s=80, alpha=0.7, label=f'真实-{name}'
    )

# 绘制错误预测的点
error_mask = y_pred_test_final != y_test_np
if np.any(error_mask):
    plt.scatter(
        x_test_pca[error_mask, 0], x_test_pca[error_mask, 1],
        c='black', marker='x', s=150, linewidths=2, label='错误预测'
    )

plt.xlabel(f'主成分1（解释方差：{pca.explained_variance_ratio_[0]:.2%}）', fontsize=12)
plt.ylabel(f'主成分2（解释方差：{pca.explained_variance_ratio_[1]:.2%}）', fontsize=12)
plt.title('BP神经网络分类结果可视化（PCA降维）', fontsize=14, fontweight='bold')
plt.legend(fontsize=10)
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('分类结果散点图.png', dpi=300, bbox_inches='tight')
plt.show()

# 6.4 总体分类准确率
train_acc = np.mean(y_pred_train_final == y_train_np)
test_acc = np.mean(y_pred_test_final == y_test_np)
print(f"\n3. 总体分类准确率：")
print(f"训练集准确率：{train_acc:.4f}")
print(f"测试集准确率：{test_acc:.4f}")

print("\n" + "=" * 60)

七、总结

在实际应用中，需要根据具体任务调整网络结构、激活函数、优化器等超参数，并结合正则化、早停等技术提高模型性能。通过不断优化和改进，BP 神经网络可以在更复杂的任务中取得更好的效果。