向量空间及其性质
向量
高中学过,有大小,有方向的量称为向量,比如力、速度、加速度等,可用有向线段 来表示向量。

相对于高中课程,线性代数中向量的定义会更加严格:

我们会尽量使用列向量来表示向量,这样更符合线性代数的习惯。我们可以通过画图来表示二维向量/三维向量的几何意义是什么。

当然三维向量也是一样:
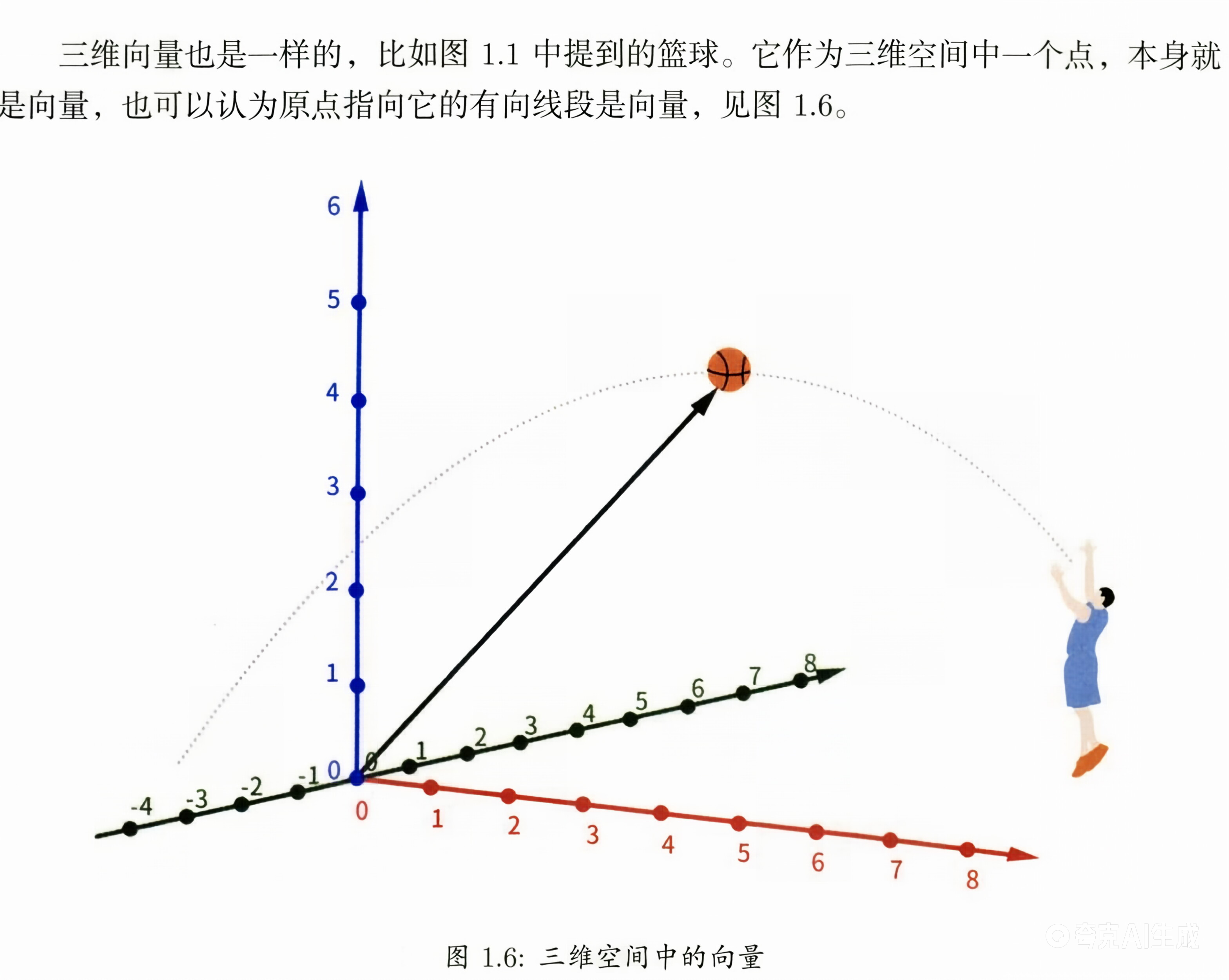
对于零向量:

向量的加法和数乘
向量加法的定义如下:
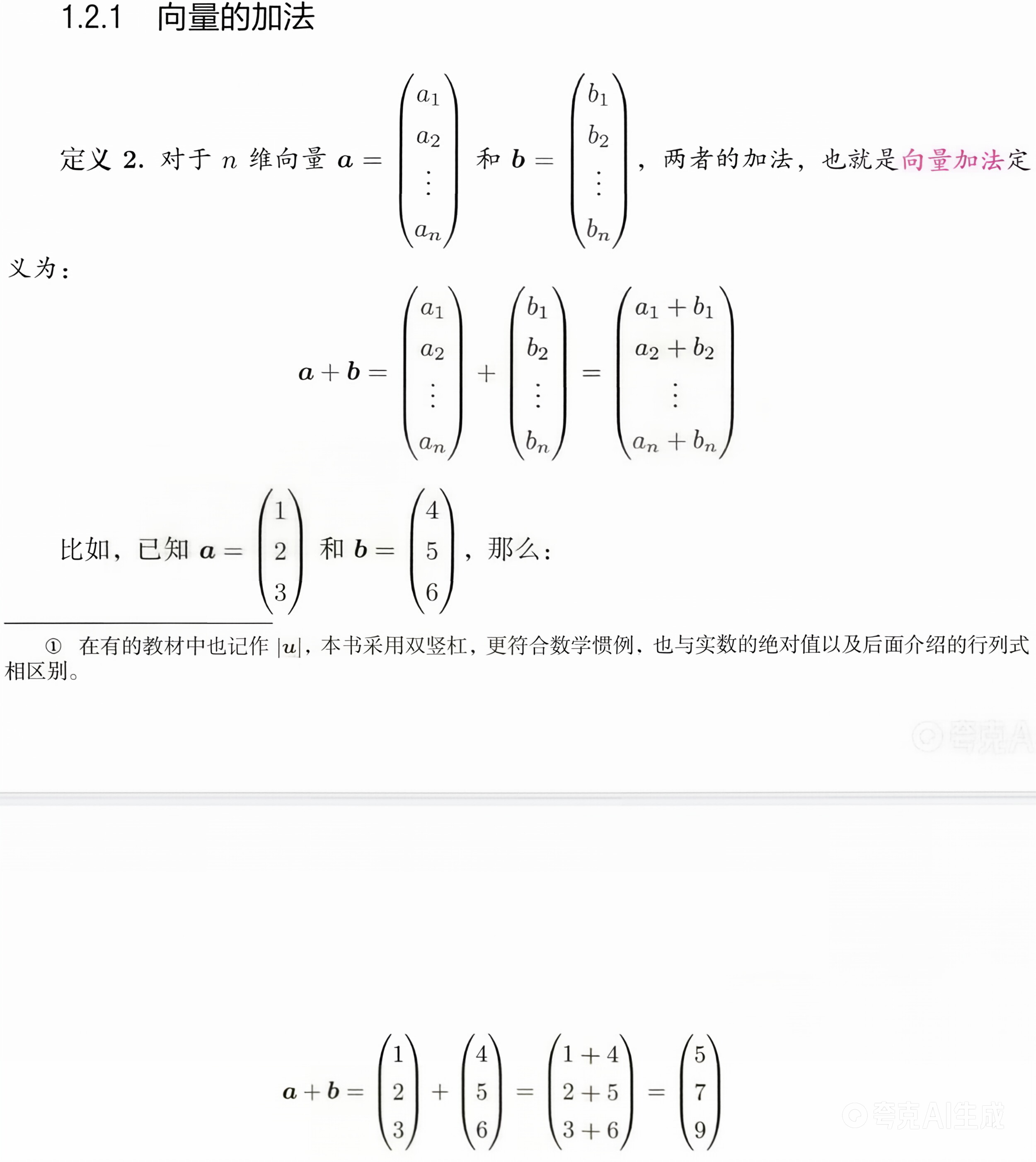
二维/三维向量加法的几何意义就是平行四边形法则或者三角形法则,这在物理中力的合成中常见。
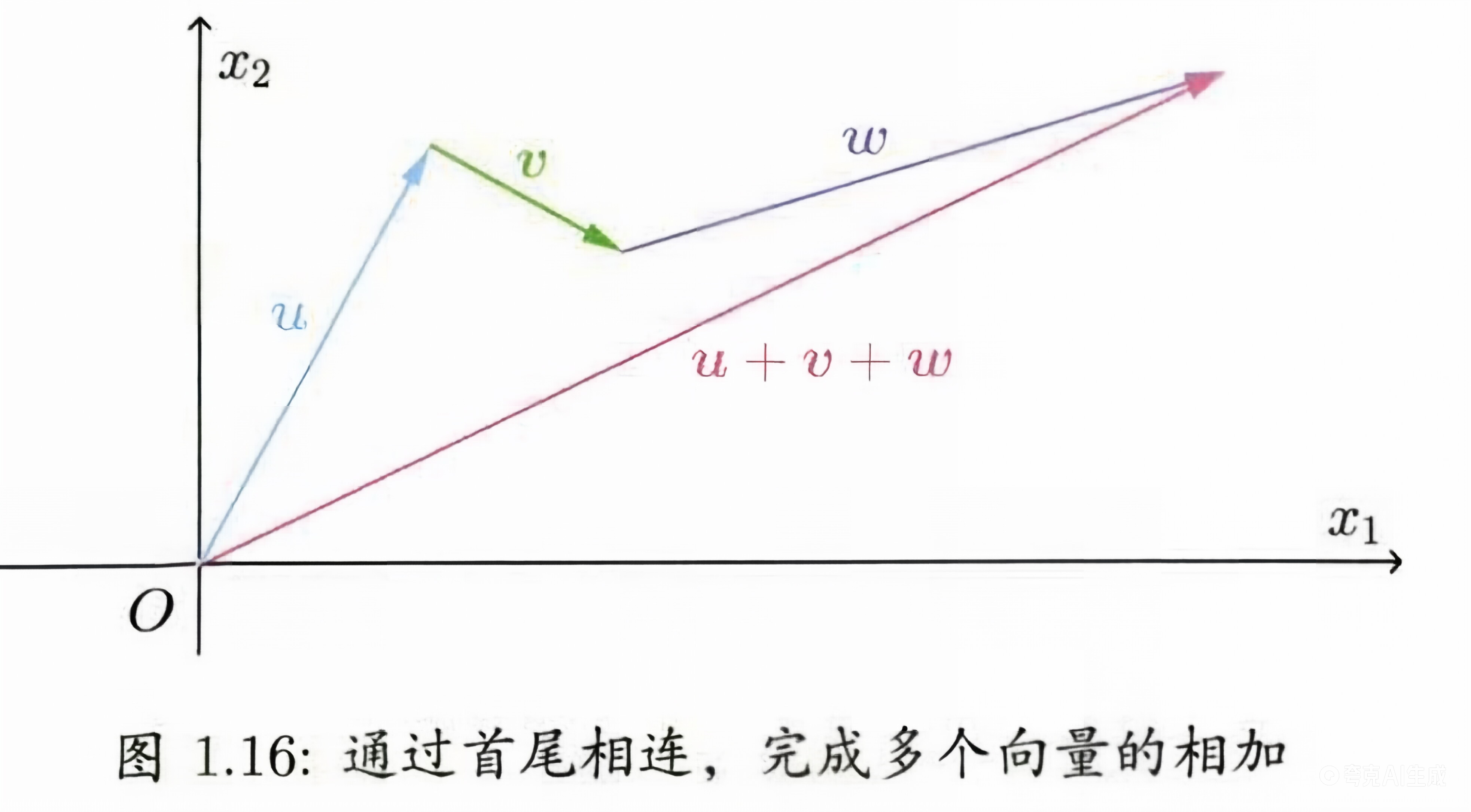
至于向量的数乘:数乘ku 就是将u 的分量扩大k倍,所以其几何意义就是对u进行伸缩,k的符号决定了伸缩的方向。
线性组合与线性相关
线性组合与线性相关是线性代数的核心概念之一,可以以混合颜色RGB来理解这个概念。


在RGB颜色空间(一个三维向量空间)中:
- 我们建立了三个坐标轴:R轴、G轴、B轴。它们两两垂直,张成了一个三维空间。
- "方向"就是颜色本身:在这个抽象空间中,从原点 (0,0,0) (代表纯黑色)出发,指向点 (255, 0, 0) 的箭头,代表的就是"纯红色"这个方向。同理,指向 (0, 255, 0) 的箭头代表"纯绿色"方向。
- "色相"由比例决定:向量 (255, 52, 85) (海棠红)和 (128, 26, 42) (同色系但更暗)在几何上指向是同一个方向,只是长度(大小)不同。因为它们三个分量 R:G:B 的比例是相同的( 255:52:85 )。这个比例就决定了颜色的"色相"。
每一个不同的比例的RGB都是一个大小/方向不同的三维向量,也可以这样理解:
- 基底:我们将纯红、纯绿、纯蓝定义为三个基向量: R = (255,0,0) , G = (0,255,0) , B = (0,0,255) 。
- 线性组合:任何颜色(向量)都可以表示为这三个基向量的线性组合(即数乘后再相加)。这正是您图片中的公式: 海棠红 = 1 * R + (52/255) * G + (85/255) * B
- 物理对应:在显示器上,每个像素点正是通过调节R、G、B三个子像素的亮度(即对基向量进行"数乘"),然后将光混合(即"向量加法")来产生最终颜色的。
下面我们给出线性相关的概念:
给定向量组 A={a1,a2,⋯ ,am}\mathcal{A} = \{ \mathbf{a_1}, \mathbf{a_2}, \cdots, \mathbf{a_m} \}A={a1,a2,⋯,am},如果存在不全为零的实数 k1,k2,⋯ ,kmk_1, k_2, \cdots, k_mk1,k2,⋯,km,使:k1a1+k2a2+⋯+kmam=0k_1 \mathbf{a_1} + k_2 \mathbf{a_2} + \cdots + k_m \mathbf{a_m} = \mathbf{0}k1a1+k2a2+⋯+kmam=0则称向量组 A\mathcal{A}A 是线性相关\textbf{线性相关}线性相关的,否则称它线性无关\textbf{线性无关}线性无关。
上述定义看上去比较复杂,其实结合上线性表示就很容易理解了:
- 如果向量组 A\mathcal{A}A 线性无关,顾名思义,说明其中的向量没有关系,或者说这些向量相互不能线性表示。比如三原色 RGB 彼此不能线性表示,说明它们没有关系,因此向量组 A={R,G,B}\mathcal{A} = \{ R, G, B \}A={R,G,B} 是线性无关的。
- 如果向量组 A\mathcal{A}A 线性相关,顾名思义,说明其中的向量有关系,或者说这些向量可以相互线性表示。比如海棠红可以由三原色线性表示,说明它们是有关系的,因此向量组 A={R,G,B,海棠红}\mathcal{A} = \{ R, G, B, \text{海棠红} \}A={R,G,B,海棠红} 是线性相关的。
下面就其中的细节再进行一下解释。
例4.\textbf{例4.}例4. 已知三原色 RGB 为如下向量,请证明向量组 A={R,G,B}\mathcal{A} = \{ \mathbf{R}, \mathbf{G}, \mathbf{B} \}A={R,G,B} 线性无关。R=(25500),G=(02550),B=(00255)R = \begin{pmatrix}255 \\ 0 \\ 0\end{pmatrix},G = \begin{pmatrix}0 \\ 255 \\ 0\end{pmatrix},B = \begin{pmatrix}0 \\ 0 \\ 255\end{pmatrix}R= 25500 ,G= 02550 ,B= 00255
证明:\textbf{证明:}证明:假设存在 k1,k2,k3k_1, k_2, k_3k1,k2,k3,使得:
k1R+k2G+k3B=k1(25500)+k2(02550)+k3(00255)=(000)k_1 \mathbf{R} + k_2 \mathbf{G} + k_3 \mathbf{B} = k_1 \begin{pmatrix} 255 \\ 0 \\ 0 \end{pmatrix} + k_2 \begin{pmatrix} 0 \\ 255 \\ 0 \end{pmatrix} + k_3 \begin{pmatrix} 0 \\ 0 \\ 255 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}k1R+k2G+k3B=k1 25500 +k2 02550 +k3 00255 = 000
即(255k1255k2255k3)=(000)即\begin{pmatrix}255k_1 \\ 255k_2 \\ 255k_3\end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}即 255k1255k2255k3 = 000
很显然上式只有在 k1=k2=k3=0k_1 = k_2 = k_3 = 0k1=k2=k3=0 时成立,所以向量组 A={R,G,B}\mathcal{A} = \{ \mathbf{R}, \mathbf{G}, \mathbf{B}\}A={R,G,B} 线性无关。