离散 Hopfield 神经网络：图像联想记忆与恢复实验

引言

Hopfield 神经网络是由美国物理学家 John Hopfield 于 1982 年提出的一种递归神经网络，属于联想记忆网络的典型代表。它能够通过训练存储多个模式，然后从部分或噪声污染的输入中恢复出完整的原始模式，具有强大的联想记忆能力。

一、Hopfield 神经网络原理

1. 网络结构

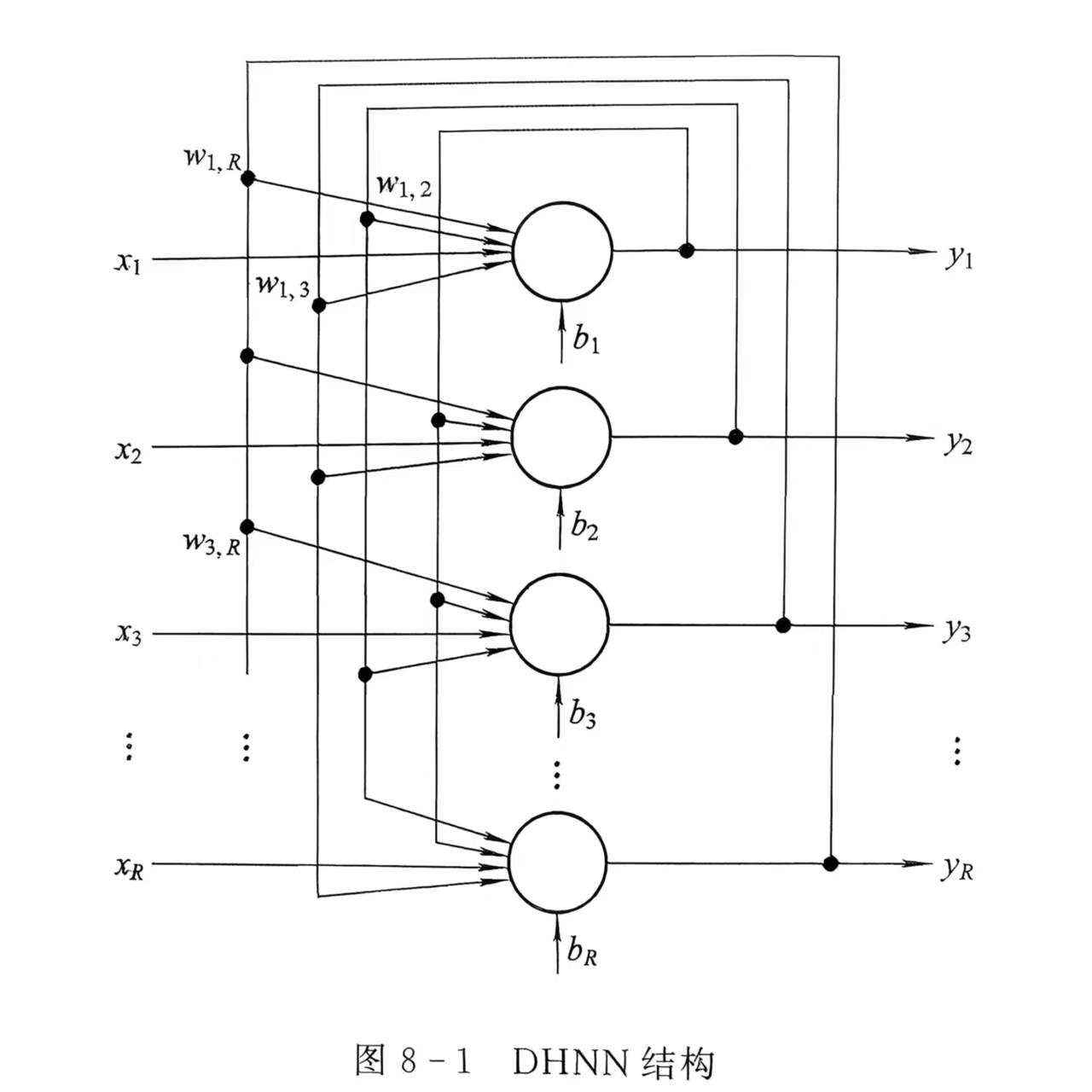
离散 Hopfield 网络是一种全连接的递归神经网络，每个神经元既作为输入也作为输出，网络结构如图所示：

2. 数学模型

神经元状态：每个神经元的状态为离散值，通常取 {-1, 1}
连接权重 ：神经元 i 到 j 的连接权重为，且（无自连接）
状态更新规则 ：

其中当，否则为 - 1

3. 学习规则

采用 Hebbian 学习规则，权重更新公式为：

其中n为神经元数量，m为存储的模式数量，为第k个模式中第i个神经元的状态。

4. 能量函数

Hopfield 网络定义了能量函数：

网络在状态更新过程中，能量函数单调递减，最终收敛到局部极小值，对应存储的模式或伪模式。

二、代码实现

1. 网络类定义

python 复制代码

class HopfieldNetwork:
    """离散Hopfield神经网络"""

    def __init__(self, num_neurons):
        self.num_neurons = num_neurons
        self.weights = np.zeros((num_neurons, num_neurons))

    def train(self, patterns):
        """训练网络"""
        for i in range(self.num_neurons):
            for j in range(self.num_neurons):
                if i != j:
                    self.weights[i, j] = (1 / self.num_neurons) * np.sum(patterns[:, i] * patterns[:, j])

    def predict(self, pattern, max_iter=100):
        """恢复模式"""
        current = pattern.copy()
        for _ in range(max_iter):
            order = np.random.permutation(self.num_neurons)
            new_state = current.copy()
            for idx in order:
                activation = np.dot(self.weights[idx, :], current)
                new_state[idx] = 1 if activation >= 0 else -1
            if np.array_equal(new_state, current):
                break
            current = new_state
        return current

2. 模式创建

python 复制代码

def create_patterns(size=10):
    """创建树和笑脸模式"""
    tree = np.ones((size, size)) * -1
    smile = np.ones((size, size)) * -1

    # 树图案
    for i in range(3):
        tree[i + 1, (3 - i):(7 + i)] = 1
    tree[4:7, 4:6] = 1

    # 笑脸图案
    smile[3, 3] = smile[3, 6] = 1
    smile[5, [2, 7]] = 1
    smile[6, 3:7] = 1

    return tree, smile

3. 噪声添加

python 复制代码

def add_noise(pattern, noise_level):
    """添加噪声"""
    noisy = pattern.copy()
    pixels = pattern.size
    flip_count = int(noise_level * pixels)
    indices = np.random.choice(pixels, flip_count, replace=False)
    rows, cols = pattern.shape
    for idx in indices:
        r, c = idx // cols, idx % cols
        noisy[r, c] *= -1
    return noisy

4. 主函数流程

python 复制代码

def main():
    img_size = 10
    tree, smile = create_patterns(img_size)

    # 训练网络
    patterns = np.array([tree.flatten(), smile.flatten()])
    net = HopfieldNetwork(img_size * img_size)
    net.train(patterns)

    # 测试不同噪声水平
    noise_levels = [0.1, 0.2, 0.15, 0.25]
    test_images = [
        add_noise(tree, noise_levels[0]),
        add_noise(smile, noise_levels[1]),
        add_noise(tree, noise_levels[2]),
        add_noise(smile, noise_levels[3])
    ]

    # 恢复图像
    recovered = []
    for img in test_images:
        recovered_flat = net.predict(img.flatten())
        recovered.append(recovered_flat.reshape(img_size, img_size))

    # 可视化结果
    # ...（省略可视化代码）

三、完整代码

python 复制代码

import numpy as np
import matplotlib.pyplot as plt


class HopfieldNetwork:
    """离散Hopfield神经网络"""

    def __init__(self, num_neurons):
        self.num_neurons = num_neurons
        self.weights = np.zeros((num_neurons, num_neurons))

    def train(self, patterns):
        """训练网络"""
        for i in range(self.num_neurons):
            for j in range(self.num_neurons):
                if i != j:
                    self.weights[i, j] = (1 / self.num_neurons) * np.sum(patterns[:, i] * patterns[:, j])

    def predict(self, pattern, max_iter=100):
        """恢复模式"""
        current = pattern.copy()
        for _ in range(max_iter):
            order = np.random.permutation(self.num_neurons)
            new_state = current.copy()
            for idx in order:
                activation = np.dot(self.weights[idx, :], current)
                new_state[idx] = 1 if activation >= 0 else -1
            if np.array_equal(new_state, current):
                break
            current = new_state
        return current


def create_patterns(size=10):
    """创建树和笑脸模式"""
    tree = np.ones((size, size)) * -1
    smile = np.ones((size, size)) * -1

    # 树图案
    for i in range(3):
        tree[i + 1, (3 - i):(7 + i)] = 1
    tree[4:7, 4:6] = 1

    # 笑脸图案
    smile[3, 3] = smile[3, 6] = 1
    smile[5, [2, 7]] = 1
    smile[6, 3:7] = 1

    return tree, smile


def add_noise(pattern, noise_level):
    """添加噪声"""
    noisy = pattern.copy()
    pixels = pattern.size
    flip_count = int(noise_level * pixels)
    indices = np.random.choice(pixels, flip_count, replace=False)
    rows, cols = pattern.shape
    for idx in indices:
        r, c = idx // cols, idx % cols
        noisy[r, c] *= -1
    return noisy


def main():
    img_size = 10
    tree, smile = create_patterns(img_size)

    # 训练网络
    patterns = np.array([tree.flatten(), smile.flatten()])
    net = HopfieldNetwork(img_size * img_size)
    net.train(patterns)

    # 测试不同噪声水平
    noise_levels = [0.1, 0.2, 0.15, 0.25]
    test_images = [
        add_noise(tree, noise_levels[0]),
        add_noise(smile, noise_levels[1]),
        add_noise(tree, noise_levels[2]),
        add_noise(smile, noise_levels[3])
    ]

    # 恢复图像
    recovered = []
    for img in test_images:
        recovered_flat = net.predict(img.flatten())
        recovered.append(recovered_flat.reshape(img_size, img_size))

    # 可视化结果
    fig, axes = plt.subplots(2, 4, figsize=(12, 6))
    titles = [
        ['Tree+10%', 'Recovered', 'Tree+15%', 'Recovered'],
        ['Smile+20%', 'Recovered', 'Smile+25%', 'Recovered']
    ]

    for i in range(2):
        for j in range(4):
            idx = i * 2 + j // 2
            img = test_images[idx] if j % 2 == 0 else recovered[idx]
            axes[i, j].imshow(img, cmap='binary')
            axes[i, j].set_title(titles[i][j])
            axes[i, j].axis('off')

    plt.suptitle('Hopfield Network - Image Recovery')
    plt.tight_layout()
    plt.show()


if __name__ == "__main__":
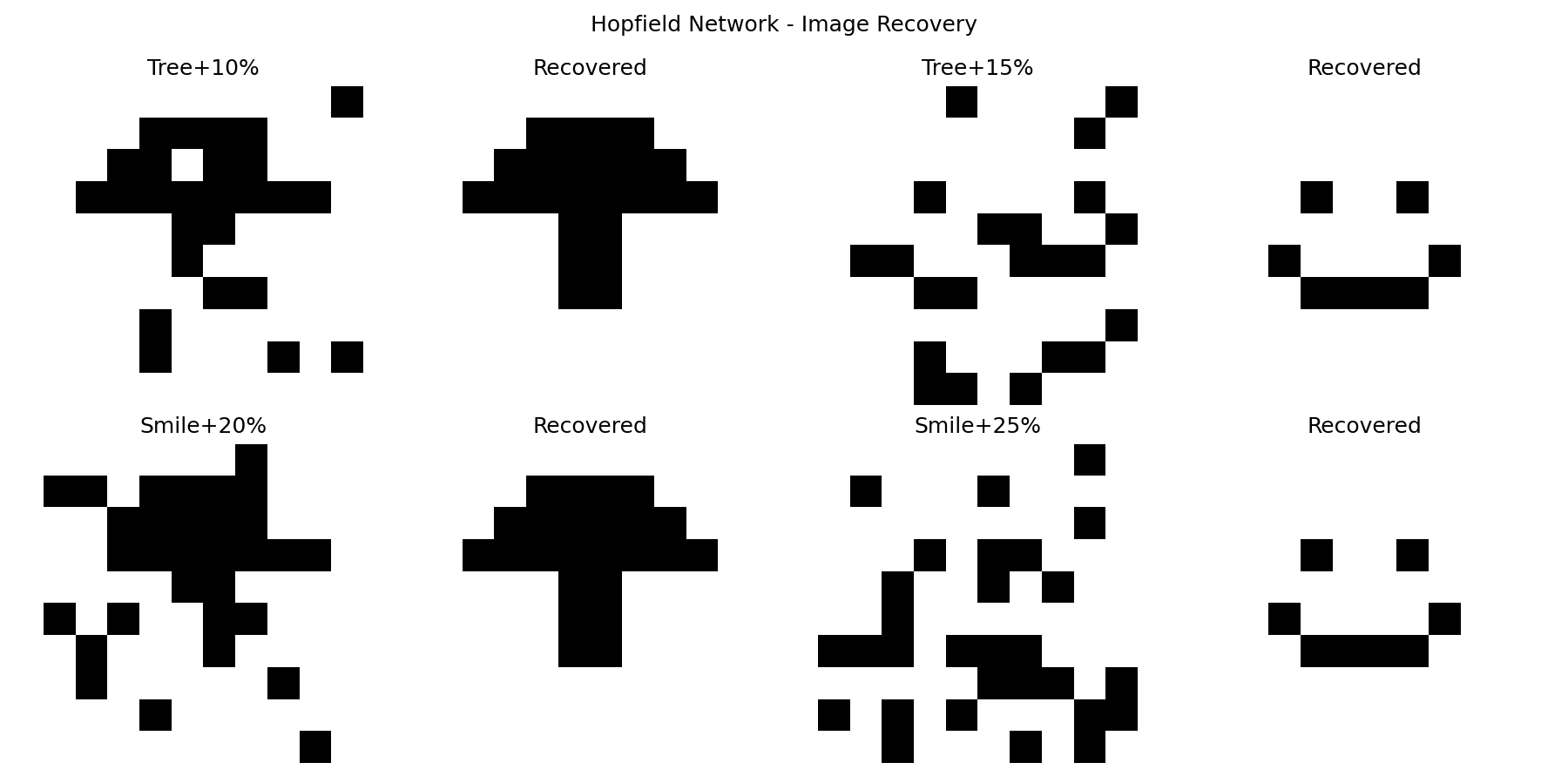
    main()

四、实验结果

五、Hopfield 网络的应用领域

图像恢复：从噪声污染的图像中恢复原始图像
模式识别：识别部分缺失或变形的模式
优化计算：求解旅行商问题（TSP）等组合优化问题
联想记忆：模拟人类的联想记忆能力
故障诊断：从故障症状中推断故障原因

六、总结与展望

1. 实验总结

Hopfield 网络能够从噪声污染的输入中恢复原始模式
恢复效果随噪声水平增加而下降
对于简单模式，在 20% 噪声水平下仍能较好恢复

2. 局限性

存储容量有限，约为神经元数量的 15%
容易收敛到伪模式
对于复杂模式恢复效果不佳
训练过程是一次性的，难以增量学习

3. 改进方向

连续 Hopfield 网络：使用连续状态和 sigmoid 激活函数
Boltzmann 机：引入随机机制，避免陷入局部极小值
受限玻尔兹曼机（RBM）：通过限制连接方式提高学习效率
深度信念网络（DBN）：堆叠多个 RBM，提高特征学习能力