OpenCV 学习5-你知道图像旋转的原理吗？

图像旋转是图像处理的一个常见操作。OpenCV提供了函数来实现图像的旋转。本文主要介绍实现图像旋转的数学原理、getRotationMatrix2D()函数、warpAffine()函数。

1、旋转之数学原理

对线性代数不熟悉的读者，博主建议先看： 数学基础-线性代数-学习系列

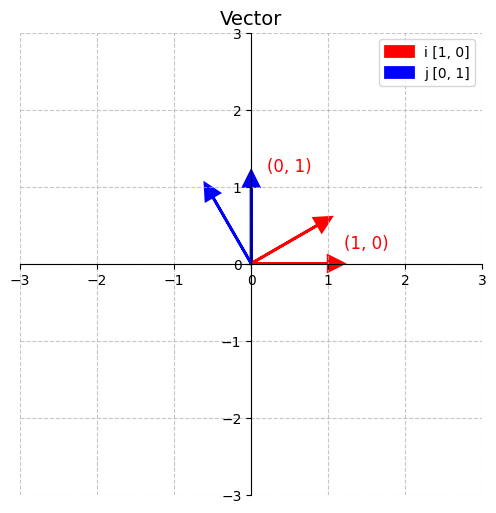
• 一个长度为1指向右边的向量，称作ihat，x方向的单位向量 i ^ \hat{i} i^
• 一个长度为1垂直向上的向量，称作jhat，y方向的单位向量 j ^ \hat{j} j^
  i ^ = [ 1 0 ] , j ^ = [ 0 1 ] \hat{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix},\quad \hat{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} i^=[10],j^=[01]
  基向量围绕原点 逆时针旋转30度。 i ^ \hat{i} i^ 和 j ^ \hat{j} j^ 分别落在

  c o s θ sin ⁡ θ \] , \[ − sin ⁡ θ c o s θ \] \\begin{bmatrix} cos\\theta \\\\ \\sin\\theta \\end{bmatrix},\\quad \\begin{bmatrix} -\\sin\\theta \\\\ cos\\theta \\end{bmatrix} \[cosθsinθ\],\[−sinθcosθ

在二维平面上，一个点 ( x , y ) (x, y) (x,y)绕原点逆时针旋转角度 θ \theta θ 后的新坐标 ( x ′ , y ′ ) (x', y') (x′,y′)可表示为：

x ′ y ′ \] = \[ c o s θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ \] \[ x y \] \\begin{bmatrix} x' \\\\ y' \\end{bmatrix} =\\begin{bmatrix} cos\\theta \& -\\sin\\theta \\\\ \\sin\\theta \& \\cos\\theta \\end{bmatrix} \\begin{bmatrix} x \\\\ y \\end{bmatrix} \[x′y′\]=\[cosθsinθ−sinθcosθ\]\[xy

即：
x ′ = x cos ⁡ θ − y sin ⁡ θ y ′ = x sin ⁡ θ + y cos ⁡ θ x' = x \cos\theta - y \sin\theta \\ y' = x \sin\theta + y \cos\theta x′=xcosθ−ysinθy′=xsinθ+ycosθ

---

2、图像旋转原理

⚠️ 注意：默认坐标系原点在左上角， x x x 向右， y y y 向下。

由于图像的坐标原点位于左上角，若直接使用上述公式，会导致图像绕左上角旋转，造成严重偏移。

✅ 正确做法是让图像 绕其中心点旋转，需执行以下三步：

1. 平移图像：将旋转中心移到原点
2. 应用旋转：使用旋转矩阵
3. 平移回去：将图像恢复到原始坐标系

这称为 "以某点为中心的旋转变换" ，这是一个线性复合变换

---

图像旋转的数学过程：平移 → 旋转 → 平移回

在图像处理中，若要实现"以图像中心为轴心"的旋转操作（如常见的图像顺时针/逆时针旋转），不能直接使用简单的旋转变换。否则图像会绕坐标原点旋转，导致部分区域移出画布。

为此，通常采用三步法：

1. 平移到原点 → 2. 旋转 → 3. 平移回去

这一过程属于仿射变换（Affine Transformation的一种典型应用。

2.1 图像旋转示例

假设我们要将一幅图像绕其中心点逆时针旋转角度 θ θ θ。

设原始图像大小为 W × H W \times H W×H，其中心点坐标 为：
( c x , c y ) = ( W 2 , H 2 ) (c_x, c_y) = \left( \frac{W}{2}, \frac{H}{2} \right) (cx,cy)=(2W,2H)

我们希望将图像中任意一点 ( x , y ) (x, y) (x,y) 绕该中心逆时针旋转 θ \theta θ 角度 ，得到新坐标 ( x ′ , y ′ ) (x', y') (x′,y′)。

整个变换分为以下三个步骤。

---

🔹 第一步：平移到原点（以中心为原点）

将图像整体平移，使中心点移动到坐标原点：
{ x 1 = x − c x y 1 = y − c y ⇒ [ x 1 y 1 ] = [ x y ] − [ c x c y ] \begin{cases} x_1 = x - c_x \\ y_1 = y - c_y \end{cases} \quad \Rightarrow \quad \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} = \begin{bmatrix} x \\ y \end{bmatrix} - \begin{bmatrix} c_x \\ c_y \end{bmatrix} {x1=x−cxy1=y−cy⇒[x1y1]=[xy]−[cxcy]

此时，图像以 ( 0 , 0 ) (0,0) (0,0) 为中心，便于进行标准旋转变换。

---

🔹 第二步：绕原点旋转 θ \theta θ

使用二维旋转矩阵对点 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) 进行逆时针旋转：

x 2 y 2 \] = \[ cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ \] \[ x 1 y 1 \] \\begin{bmatrix} x_2 \\\\ y_2 \\end{bmatrix} = \\begin{bmatrix} \\cos\\theta \& -\\sin\\theta \\\\ \\sin\\theta \& \\cos\\theta \\end{bmatrix} \\begin{bmatrix} x_1 \\\\ y_1 \\end{bmatrix} \[x2y2\]=\[cosθsinθ−sinθcosθ\]\[x1y1

展开为：
{ x 2 = x 1 cos ⁡ θ − y 1 sin ⁡ θ y 2 = x 1 sin ⁡ θ + y 1 cos ⁡ θ \begin{cases} x_2 = x_1 \cos\theta - y_1 \sin\theta \\ y_2 = x_1 \sin\theta + y_1 \cos\theta \end{cases} {x2=x1cosθ−y1sinθy2=x1sinθ+y1cosθ

---

🔹 第三步：平移回原中心位置

将旋转后的点重新平移回原始坐标系，即加上中心偏移量：
{ x ′ = x 2 + c x y ′ = y 2 + c y ⇒ [ x ′ y ′ ] = [ x 2 y 2 ] + [ c x c y ] \begin{cases} x' = x_2 + c_x \\ y' = y_2 + c_y \end{cases} \quad \Rightarrow \quad \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} x_2 \\ y_2 \end{bmatrix} + \begin{bmatrix} c_x \\ c_y \end{bmatrix} {x′=x2+cxy′=y2+cy⇒[x′y′]=[x2y2]+[cxcy]

至此，完成了"绕中心旋转"的全过程。

---

🧮 三步合并为单个仿射变换

上述三步可合并为一个完整的仿射变换表达式：

x ′ y ′ \] = \[ cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ \] ( \[ x y \] − \[ c x c y \] ) + \[ c x c y \] \\begin{bmatrix} x' \\\\ y' \\end{bmatrix} = \\begin{bmatrix} \\cos\\theta \& -\\sin\\theta \\\\ \\sin\\theta \& \\cos\\theta \\end{bmatrix} \\left( \\begin{bmatrix} x \\\\ y \\end{bmatrix} - \\begin{bmatrix} c_x \\\\ c_y \\end{bmatrix} \\right) +\\begin{bmatrix} c_x \\\\ c_y \\end{bmatrix} \[x′y′\]=\[cosθsinθ−sinθcosθ\](\[xy\]−\[cxcy\])+\[cxcy

这对应于 OpenCV 中使用的 2×3 仿射变换矩阵 ：
M = [ cos ⁡ θ − sin ⁡ θ t x sin ⁡ θ cos ⁡ θ t y ] M = \begin{bmatrix} \cos\theta & -\sin\theta & t_x \\ \sin\theta & \cos\theta & t_y \end{bmatrix} M=[cosθsinθ−sinθcosθtxty]

其中平移项为：
t x = c x ( 1 − cos ⁡ θ ) + c y sin ⁡ θ t y = c y ( 1 − cos ⁡ θ ) − c x sin ⁡ θ t_x = c_x (1 - \cos\theta) + c_y \sin\theta \\ t_y = c_y (1 - \cos\theta) - c_x \sin\theta tx=cx(1−cosθ)+cysinθty=cy(1−cosθ)−cxsinθ

---

3、函数说明

3.1 getRotationMatrix2D

cv2.getRotationMatrix2D(center, angle, scale)

• center: 旋转中心坐标 (x, y)
• angle: 旋转角度（度）
• scale: 缩放比例（1.0 表示原尺寸)

返回一个 2x3 的仿射变换矩阵。

3.2 cv2.warpAffine(src, M, dsize)

• src: 输入图像
• M: 变换矩阵
• dsize: 输出图像大小 (width, height)

4、代码示例

在 Python 中使用 OpenCV 旋转图像非常简单，可以使用 cv2.getRotationMatrix2D() 和 cv2.warpAffine() 函数来实现图像的任意角度旋转。

import cv2
import numpy as np
import os

# 1. 读取图像
img_path = "img/dog.jpg"
if not os.path.exists(img_path):
    raise FileNotFoundError(f"未找到图像文件{img_path}")

img = cv2.imread(img_path, cv2.IMREAD_COLOR)

# 2. 获取图像的中心点
height, width = img.shape[:2]
center = (width // 2, height // 2)

# 3. 定义旋转角度（正数表示逆时针旋转）
angle = 45  # 旋转45度
scale = 1.0  # 缩放比例（1.0 表示不缩放）

# 4. 获取旋转矩阵
rotation_matrix = cv2.getRotationMatrix2D(center, angle, scale)

# 5. 执行仿射变换（旋转）
rotated_image = cv2.warpAffine(img, rotation_matrix, (width, height))

# 6. 显示原图和旋转后的图像
cv2.imshow('Original Image', img)
cv2.imshow('Rotated Image', rotated_image)

# 等待按键，然后关闭窗口
cv2.waitKey(0)
cv2.destroyAllWindows()

大家看看博主测试用图片真容

5、其它问题

5.1 避免图像被裁剪（保留完整旋转图像）

旋转后图像可能超出原始尺寸范围，导致边缘被裁剪。可通过计算新尺寸解决：

# 计算旋转后的图像尺寸
cos = abs(rotation_matrix[0, 0])
sin = abs(rotation_matrix[0, 1])

new_width = int((height * sin) + (width * cos))
new_height = int((height * cos) + (width * sin))

# 调整旋转矩阵的平移部分，使图像居中
rotation_matrix[0, 2] += (new_width / 2) - center[0]
rotation_matrix[1, 2] += (new_height / 2) - center[1]

# 应用变换
rotated_image = cv2.warpAffine(
    image,
    rotation_matrix,
    (new_width, new_height)
)

2. 修改背景颜色（默认黑色）

使用 borderValue 参数设置填充颜色（如白色）：

rotated_image = cv2.warpAffine(
    image,
    rotation_matrix,
    (new_width, new_height),
    borderValue=(255, 255, 255)  # 白色背景
)