分层可导航小世界算法（HNSW）

分层可导航小世界算法（HNSW）

引言

随着大语言模型（LLM）与检索增强生成（RAG）技术的普及与应用，向量数据库的热度持续攀升。当前主流的向量数据库（如 Milvus、Weaviate、Chroma、Elasticsearch 等）均支持 HNSW 这一高效的向量检索算法。本文将对 HNSW 算法的起源进行学习及探讨

更好的排版格式~ 传送门

正则图和随机图

在介绍 NSW 和 HNSW 之前，我们先来了解一下正则图和随机图的概念，这对于理解为什么 HNSW 能够加快向量检索效率是很有帮助的

正则图（Regular Graph）

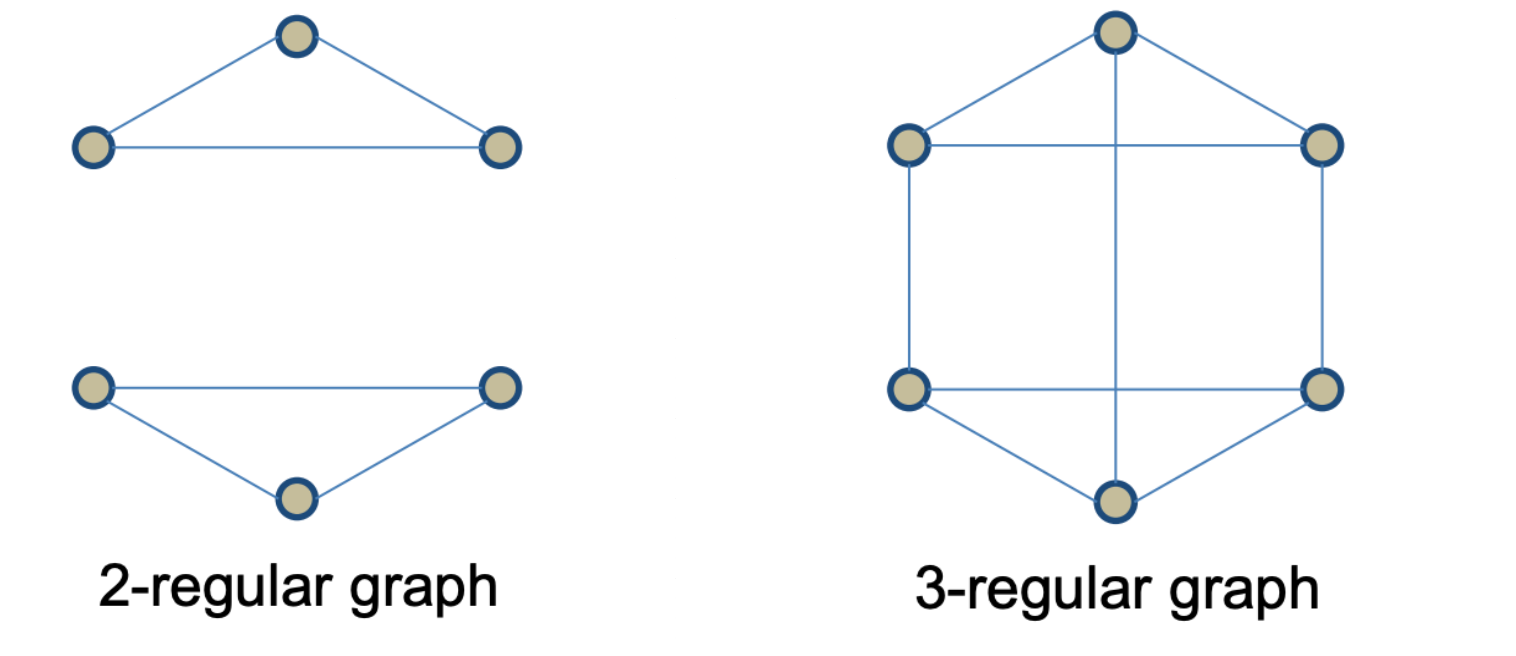
正则图是指各顶点的度均相同的无向简单图。在图论中，正则图中每个顶点具有相同数量的邻点，若每个顶点的度均为k，称为k-正则图

随机图（Random graph）

随机图是指由随机过程产生的图，一个随机图实际上是将给定的顶点之间随机地连上边

正则图 vs 随机图

• 聚类度衡量的是一个节点的邻居之间相互连接的比例
• 正则图具有较高的聚类系数，一个顶点的邻居节点之间有很多相互连接，任意两个节点之间的平均路径比较长
• 随机图具有较低的聚类系数，邻居节点之间的连接比较少，但任意两个节点之间的平均路径就可能比较短

小世界网络（NSW）

起源

在网络理论中，小世界网络 是指一类特殊的复杂网络结构，在这种网络中大部分的节点彼此并不相连，但绝大部分节点之间经过少数几步就可到达。最早观察到小世界现象的是社会人际网络。将每个人作为节点，将人与人之间的人际关系（朋友，合作，相识等）作为链接，就建立起一个社会人际网络。有时你会发现，在这样一个社会网络中，某些你觉得与你隔得很"遥远"的人，其实与你"很近"。二十世纪60年代，美国哈佛大学社会心理学家斯坦利·米尔格伦做了一个连锁信实验。他将一些信件交给自愿的参加者，要求他们通过自己的熟人将信传到信封上指明的收信人手里，他发现，296封信件中有64封最终送到了目标人物手中。而在成功传递的信件中，平均只需要5次转发，就能够到达目标。也就是说，在社会网络中，任意两个人之间的"距离"是6。这就是所谓的六度分隔 理论。 --维基百科

小世界网络具有以下性质：

• 基于规则图的随机重连过程
• 以一定概率随机重连规则图中的每条边
• 同时具备随机图与规则图的特性
  • 高聚类系数
  • 低平均路径

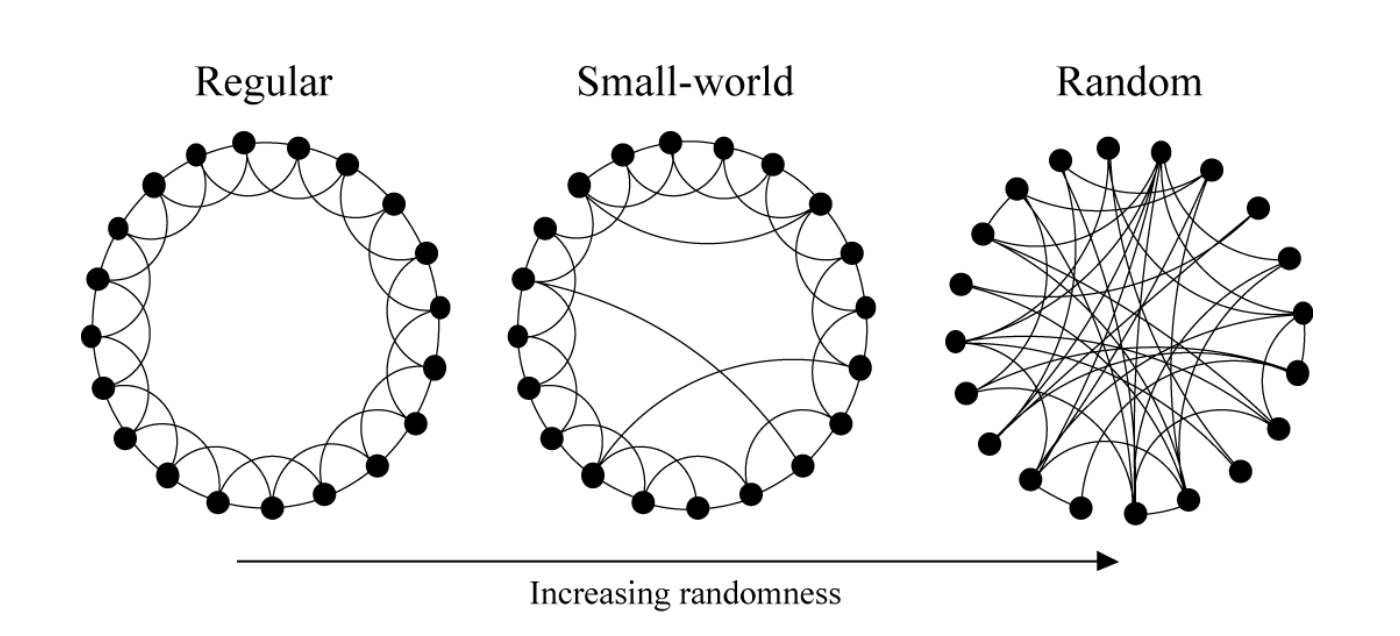
如上图所示，小世界网络介于正则图和随机图之间，小世界在局部同类节点的连接呈现出规则，但从全局来看不同类节点的连接呈现出随机性

但小世界网络还存在以下的问题：

• 网络中的任意两个节点都存在最短路径，但我们怎么去找到这个最短路径呢？
• 为什么网络中两个相互独立的节点能够通过最短路径建立连接呢？

边的构建

在 NSW 中，我们希望局部节点之间能够互相连接，也就是说具有同质性，从而使得我们检索到的大部分节点都是邻近节点。但是也希望能够保留一些"长边"（随机边），使得能够在不同的区域之间快速的跳转

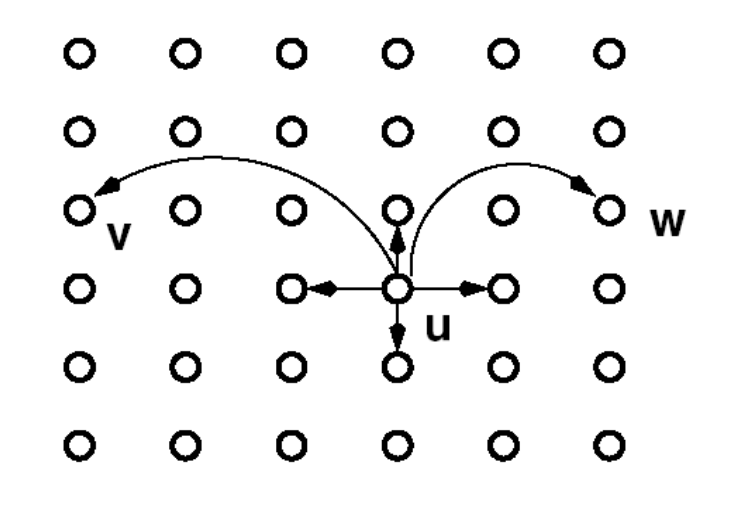
但每个节点之间的连接并不是真正的随机。如下公式所示，节点 u 与节点 v 之间是通过一定的概率来建立连接的，dim（dimension of the euclidean space）为该空间中的网络维度

P ( u → v ) ∼ 1 d ( u , v ) r P(u \to v) \sim \frac{1}{d(u,v)^{r}} P(u→v)∼d(u,v)r1

r 对搜索效率的影响

• 当r < dim时算法倾向于选择更远的邻居节点，搜索算法会快速的逼近目标区域，然后速度逐渐的衰减，但最终会找到目标节点
• 当r > dim时算法会倾向于选择更近的邻居节点，搜索算法会快速的找到较近的目标节点；但目标节点若距离较远，搜索算法会寻找的比较缓慢
• 当r==0时算法对长距离的连接是随机的，搜索算法不能保证找出最优路径
• 当r==dim时算法效果最优

当r==dim时，节点上远程连接边的个数（n）对搜索的影响

• 当n==1时，节点上只有一个远程连接的边，此时的搜索复杂度为 O(log² N)
• 当n==k时，节点拥有 k 条长程连接时，搜索成本在原来的最优基础上又降低了约 k 倍。这是因为在每个决策点，你有更多"候选路径"来尝试接近目标
  节点，搜索复杂度为 O(log² N)/k
• 当n==logN时，每个节点的长程连接数与网络节点的规模的对数相同时，网络在搜索效率上达到了理论上的极致高点，搜索复杂度来到了理论值O(log N)

应用实践：在成本可接受的范围内，增加少量长程连接边的数量，可显著提升搜索效率，也解释了弱连接的价值

NSW 进行搜索

在可导航小世界中进行搜索，搜索过程通过贪婪路由的算法实现，逐步优化来逼近目标顶点

• 贪婪路由搜索: 从起点出发（entry point），在相邻节点中识别出与查询向量最为接近的一个节点，然后转移到该顶点上。重复这一过程，直到找到一个局部最小值，停止搜索
• 停止条件: 当搜索到了一个局部最小值时，NSW 认为找到了足够相似的向量节点了，从而停止搜索
• 网络可导航的定义: 在贪婪搜索下，搜索成本（距离计算次数）随网络规模呈多项式或对数时间复杂度增长
• 贪婪路由的效率问题: 在大型网络中，如果图的结构不可导航，贪婪路由的效率可能会显著下降
• 两种路由
  • 向外扩展（zoom-out）: 搜索初期，从度数低连接较少的顶点进行搜索，有助于快速缩小范围
  • 向内搜索 zoom-in: 当进入目标大致区域后，利用度数更高连接更多的节点进行精确搜索和快速收敛

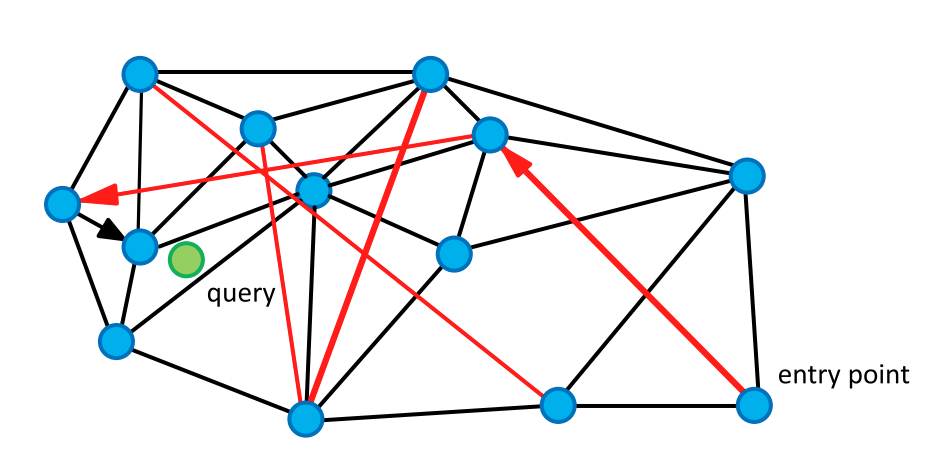
NSW 网络结构虽然有两种类型的边（长边和短边），但还是单层网络结构。搜索从随机起点（通常是低度数节点）开始，在到达一个能"看见"目标区域的枢纽节点之前，它只能在有限的局部范围内摸索，容易陷入局部最优解。并且搜索复杂度未能达到最优的对数级

分层可导航小世界（HNSW）

分层导航小世界图（Hierarchical Navigable Small World Graphs）是 NSW 的演变，它引入了概率跳表 结构中的概率多层次概念

概率跳表（Probability Skip List）

概率跳表既保留了有序数组快速查找的优点，又采用了链表结构，使得新元素的插入快速，这是不同于有序数组的实现

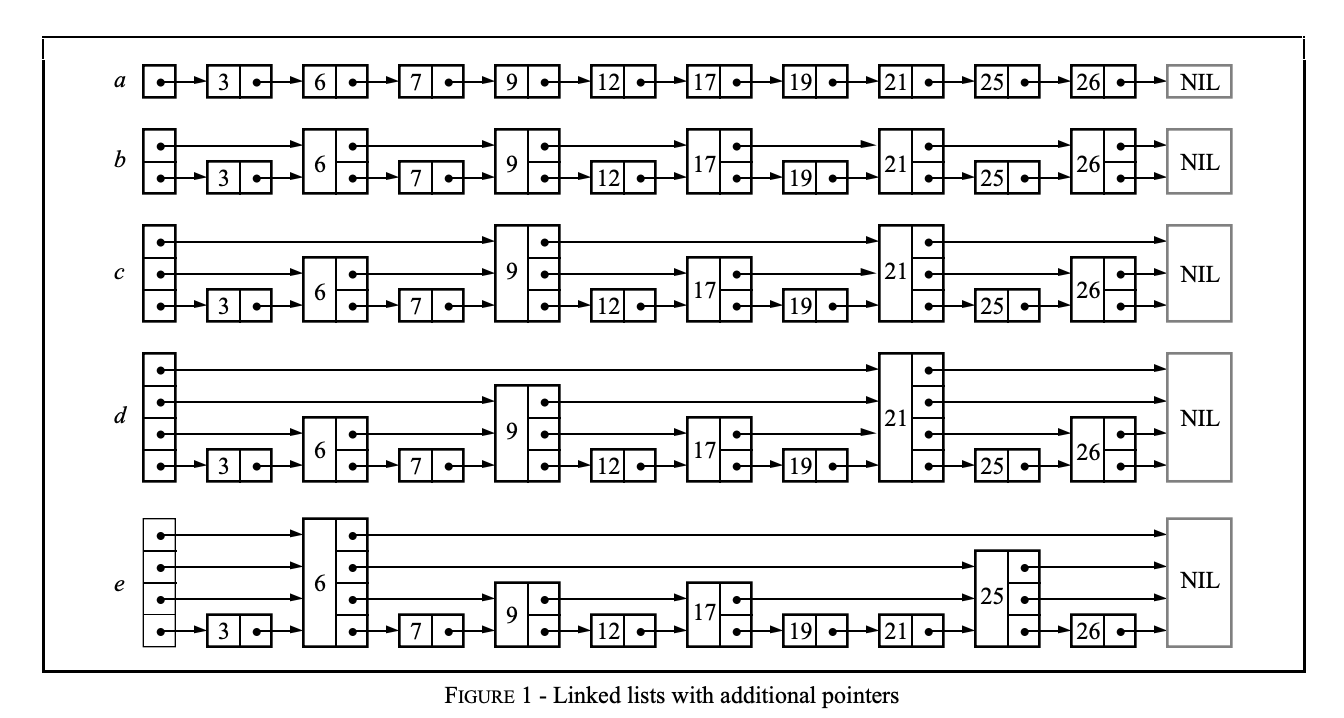
跳表通过构建多层链表来工作

• 在第一层（最高层），链接会跳过许多中间节点。随着层数下降，每个链接所"跳过"的节点数逐层减少
• 在跳表中搜索时，我们从最高层开始，沿着指针向右移动。如果发现当前节点的键值大于我们要查找的键值，就意味着我们已经越过了目标节点。此时，我们退回到前一个节点，并下降至下一层继续搜索
• 概率跳表中的每一层都会完整包含上一层的所有节点

HNSW 继承了相同的分层结构格式：最高层包含最长的连接（用于快速搜索），而较低层包含较短的连接（用于精确搜索）

分层次网络结构

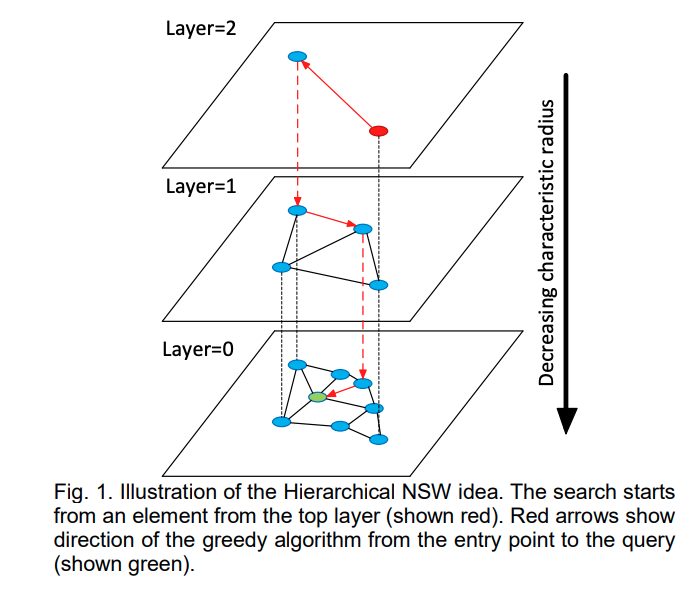
HNSW 通过向 NSW 中添加层次化网络结构，创建一个在不同层级具有不同连接长度的图

• 在网络最高层的节点拥有最长的连接 ，在网络最低层的节点拥有最短的连接
• 最高层作为入口点，仅包含最长的连接，有助于快速跨越较大的范围
• 网络中的每一层会完整包含上一层的全部节点
• 随着向下层级的移动，连接逐渐变短且数量增多，这有助于在局部区域内进行更精细的搜索
• 和 NSW 相同，通过贪婪路由策略，遍历每一层的链接，逐步向最近的顶点移动，直至达到局部最小值
• 和 NSW 不同的是 ，在达到局部最小值后，搜索不会停止，而是转移到当前顶点在下一层的对应点，并在那里重新开始搜索
• 搜索过程会再每一层重复，直到达到最底层并找到该层的局部最小值为止

分层图的构建

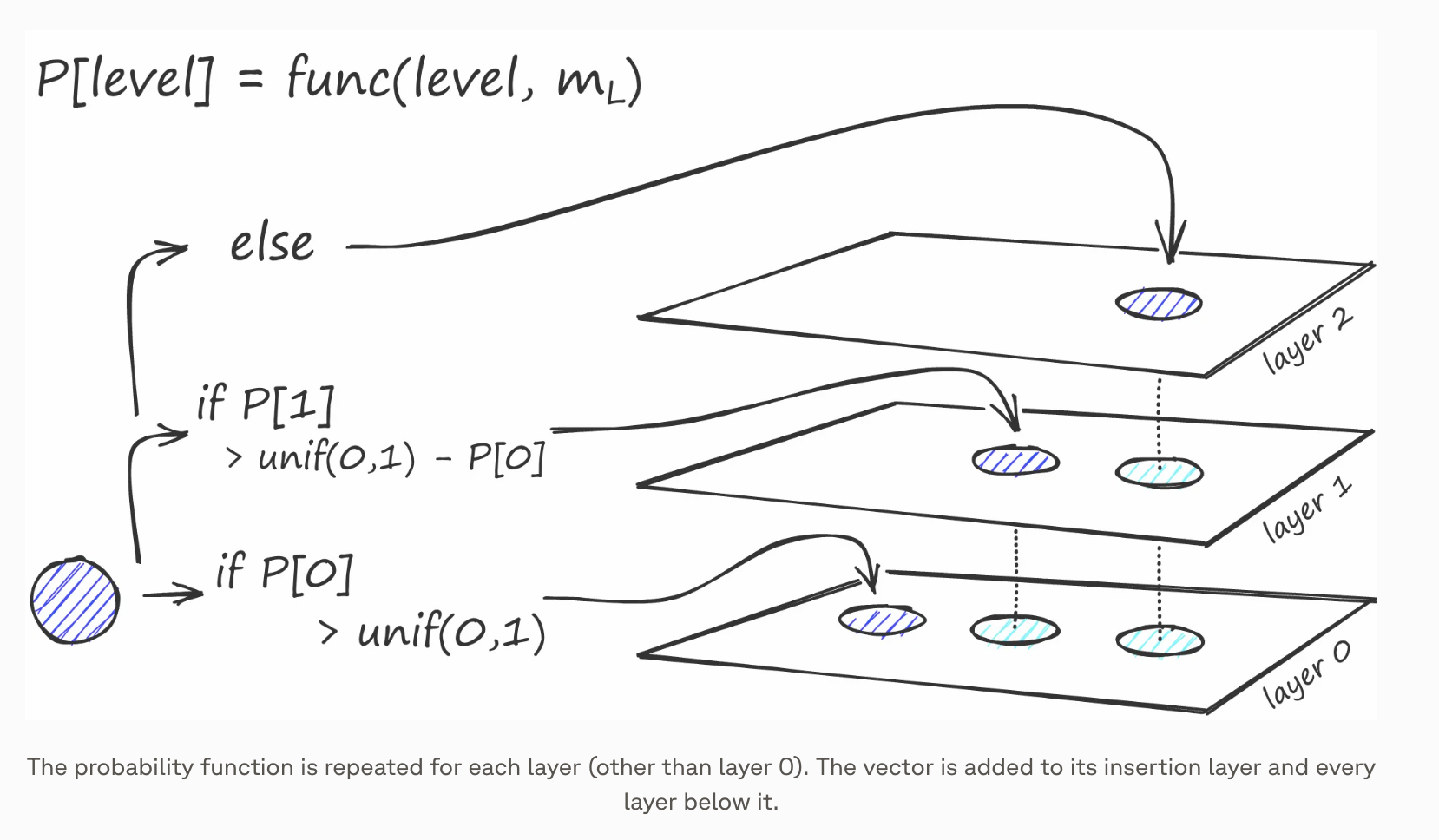
在图构建过程中，向量被逐个迭代插入。总层数由参数 L 表示。向量被插入到某一特定层的概率由一个概率函数给出

• 概率插入：每个新插入的节点，都会以一个随层高递减的概率被分配到更高的层。这确保了上层节点数较少，形成一种类似"跳表"的随机分层结构
• m_l参数：控制着节点被插入到更高层的衰减速率，其值越小，节点出现在高层的概率就越低，当其值趋于0时，所有向量都会被存入第0层，网络退化成了 NSW
• 最小化各层之间共享邻居的重叠 时，能达到最佳性能，减少m_l的值有助于减少重叠，但是会增加搜索时的平均遍历次数。一个理论经验值是1/ln(m_l)
• 图的构建从顶层开始。进入图后，算法沿边进行贪婪遍历，为待插入向量 q 找到最近的 ef 个邻居------此时 ef = 1
• 找到局部最小值后，算法下降至下一层（与搜索过程类似）。此过程重复进行，直至到达我们选择的插入层
• 构建进入第二阶段，此时 ef 值增加到 efConstruction（这是我们设置的参数），意味着将返回更多的最近邻居。在第二阶段，这些最近邻居会作为新插入元素 q 建立连接的候选对象，同时也作为下一层的入口点
• 从这些候选对象中，会添加 M 个邻居作为链接------最直接的选择标准是选取距离最近的向量
• 添加连接时还需要考虑两个参数 ：M_max:它定义了一个顶点可拥有连接的最大数量; M_max0:第0层顶点的最大连接数
• 插入的停止条件是在层 0 中找到局部最小值

参考文献

• 1\] [HNSW的基本原理及使用](https://zhuanlan.zhihu.com/p/264832755)

• 3\] [大白话理解HNSW](https://juejin.cn/post/7082579087776022541)

  neighbor search using Hierarchical Navigable
  Small World graphs](https://arxiv.org/pdf/1603.09320)

• 5\] [Hierarchical Navigable Small Worlds (HNSW)](https://www.pinecone.io/learn/series/faiss/hnsw/)

  Balanced Trees](https://15721.courses.cs.cmu.edu/spring2018/papers/08-oltpindexes1/pugh-skiplists-cacm1990.pdf)