你是否好奇过,手机相册如何自动将照片分为"人像"、"风景"和"美食"?电商网站如何知道"买了这本书的人也可能喜欢那本书"?这些看似智能的背后,都藏着一个简单而强大的机器学习算法------K-均值聚类。
用生活场景类比+可视化演示+极简代码实践,带你轻松入门第一个无监督学习算法。今天我们来聊一个既经典又直观的机器学习算法------k-均值聚类。我会尽量不用复杂公式,带大家从生活场景出发,通过可视化演示和简单代码实践,真正理解这个算法的精髓。
一、从生活场景说起:什么是"物以类聚"?
场景1:操场上重新分班
想象一下,学校要求全校同学在操场上重新组成5个新班级,但没有名单,只告诉你要组成5个班。你会怎么做?
你可能会:
-
找认识的同学
-
找穿同样队服的人
-
慢慢观察,和看起来"合群"的人站在一起
这本质上就是根据"相似性"进行"聚类"------我们今天要学的,就是让计算机自动完成这件事的方法。
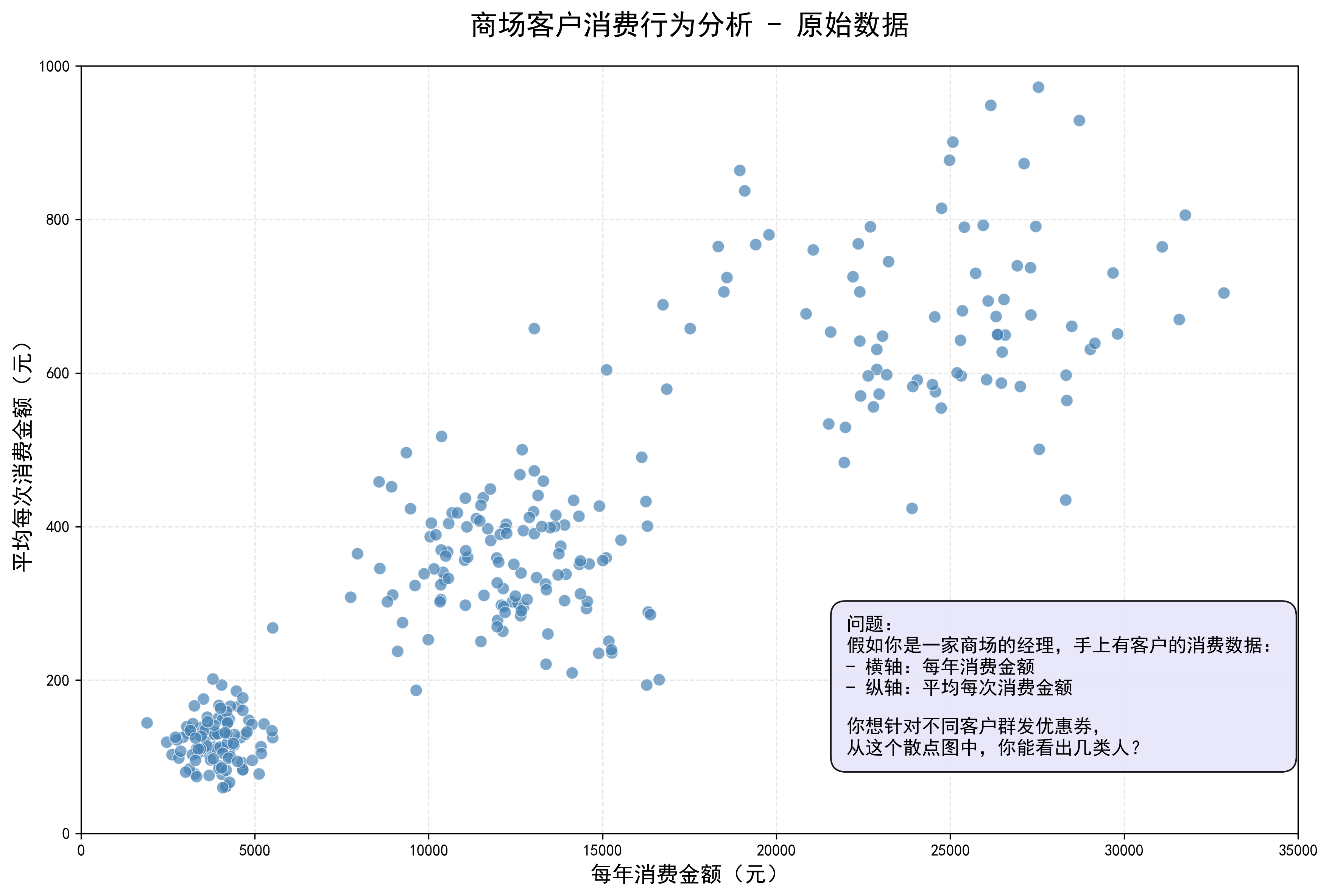
场景2:商场客户分组
假如你是一家商场的经理,手上有客户的消费数据:
-
横轴:每年消费金额
-
纵轴:平均每次消费金额
你想针对不同客户群发优惠券,从下面的散点图中,你能看出几类人?
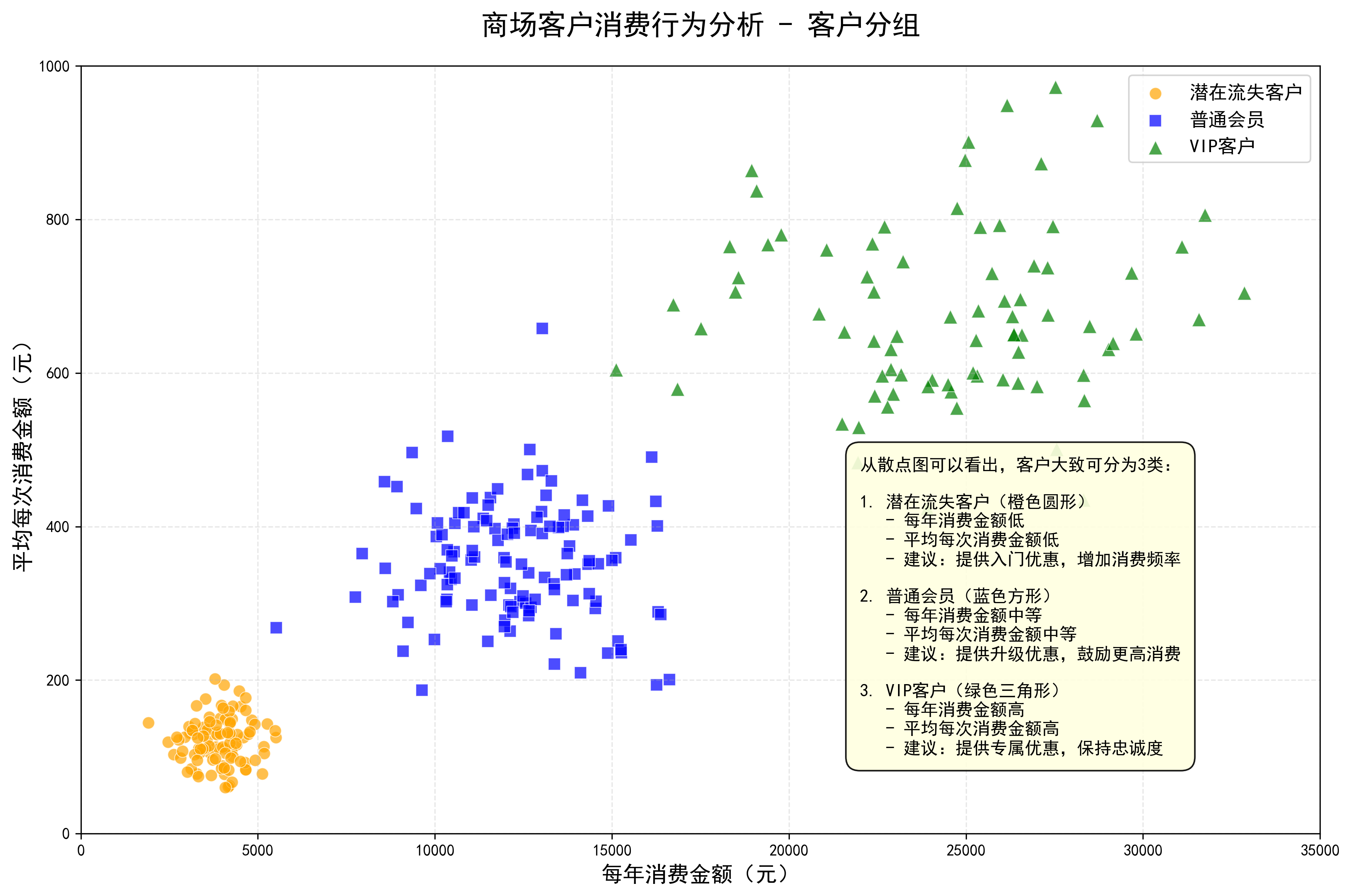
通常我们能看出:
-
高消费高频次(VIP客户)
-
低消费低频次(潜在流失客户)
-
中等消费群体(普通会员)
python
import numpy as np
import matplotlib.pyplot as plt
import os
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
# 创建用于保存图片的子文件夹
output_folder = "商场客户分析图表"
if not os.path.exists(output_folder):
os.makedirs(output_folder)
print(f"已创建文件夹: {output_folder}")
else:
print(f"文件夹已存在: {output_folder}")
# 生成模拟客户数据
np.random.seed(42) # 确保结果可重复
# 1. 低消费低频次(潜在流失客户)
low_spenders = np.random.normal(loc=[4000, 120], scale=[800, 30], size=(100, 2))
# 2. 中等消费群体(普通会员)
medium_spenders = np.random.normal(loc=[12000, 350], scale=[2000, 80], size=(120, 2))
# 3. 高消费高频次(VIP客户)
high_spenders = np.random.normal(loc=[25000, 700], scale=[4000, 120], size=(80, 2))
# 合并所有数据
all_data = np.vstack([low_spenders, medium_spenders, high_spenders])
# 创建散点图
fig, ax = plt.subplots(figsize=(12, 8))
# 用不同颜色和形状标记不同类型的客户
scatter1 = ax.scatter(low_spenders[:, 0], low_spenders[:, 1],
c='orange', alpha=0.7, s=60, edgecolors='white', linewidth=0.5,
marker='o', label='潜在流失客户')
scatter2 = ax.scatter(medium_spenders[:, 0], medium_spenders[:, 1],
c='blue', alpha=0.7, s=60, edgecolors='white', linewidth=0.5,
marker='s', label='普通会员')
scatter3 = ax.scatter(high_spenders[:, 0], high_spenders[:, 1],
c='green', alpha=0.7, s=80, edgecolors='white', linewidth=0.5,
marker='^', label='VIP客户')
# 设置图表标题和标签
ax.set_title('商场客户消费行为分析 - 客户分组', fontsize=18, fontweight='bold', pad=20)
ax.set_xlabel('每年消费金额(元)', fontsize=14)
ax.set_ylabel('平均每次消费金额(元)', fontsize=14)
# 添加图例
ax.legend(fontsize=12, loc='upper right')
# 添加网格线
ax.grid(True, alpha=0.3, linestyle='--')
# 设置坐标轴范围
ax.set_xlim(0, 35000)
ax.set_ylim(0, 1000)
# 在图上添加说明文字
analysis_text = "从散点图可以看出,客户大致可分为3类:\n\n" \
"1. 潜在流失客户(橙色圆形)\n" \
" - 每年消费金额低\n" \
" - 平均每次消费金额低\n" \
" - 建议:提供入门优惠,增加消费频率\n\n" \
"2. 普通会员(蓝色方形)\n" \
" - 每年消费金额中等\n" \
" - 平均每次消费金额中等\n" \
" - 建议:提供升级优惠,鼓励更高消费\n\n" \
"3. VIP客户(绿色三角形)\n" \
" - 每年消费金额高\n" \
" - 平均每次消费金额高\n" \
" - 建议:提供专属优惠,保持忠诚度"
plt.text(22000, 100, analysis_text,
fontsize=11,
bbox=dict(boxstyle="round,pad=0.8", facecolor="lightyellow", alpha=0.9),
verticalalignment='bottom')
plt.tight_layout()
# 保存图片到子文件夹
output_path = os.path.join(output_folder, "商场客户分组散点图.png")
plt.savefig(output_path, dpi=300, bbox_inches='tight')
print(f"已保存图片到: {output_path}")
plt.show()
# 创建第二张图:未分组的散点图,让用户自己观察
fig2, ax2 = plt.subplots(figsize=(12, 8))
# 绘制所有客户数据
scatter_all = ax2.scatter(all_data[:, 0], all_data[:, 1],
c='steelblue', alpha=0.7, s=60,
edgecolors='white', linewidth=0.5)
# 设置图表标题和标签
ax2.set_title('商场客户消费行为分析 - 原始数据', fontsize=18, fontweight='bold', pad=20)
ax2.set_xlabel('每年消费金额(元)', fontsize=14)
ax2.set_ylabel('平均每次消费金额(元)', fontsize=14)
# 添加网格线
ax2.grid(True, alpha=0.3, linestyle='--')
# 设置坐标轴范围
ax2.set_xlim(0, 35000)
ax2.set_ylim(0, 1000)
# 添加问题描述
question_text = "问题:\n" \
"假如你是一家商场的经理,手上有客户的消费数据:\n" \
"- 横轴:每年消费金额\n" \
"- 纵轴:平均每次消费金额\n\n" \
"你想针对不同客户群发优惠券,\n" \
"从这个散点图中,你能看出几类人?"
plt.text(22000, 100, question_text,
fontsize=12,
bbox=dict(boxstyle="round,pad=0.8", facecolor="lavender", alpha=0.9),
verticalalignment='bottom')
plt.tight_layout()
# 保存第二张图片到子文件夹
output_path2 = os.path.join(output_folder, "商场客户原始数据散点图.png")
plt.savefig(output_path2, dpi=300, bbox_inches='tight')
print(f"已保存图片到: {output_path2}")
plt.show()
print(f"\n所有图片已保存到 '{output_folder}' 文件夹中")-
第一张图:已分组的散点图
-
用不同颜色和形状标记了三种客户类型
-
添加了详细的客户类型说明
-
保存为"商场客户分组散点图.png"
-
-
第二张图:原始数据散点图
-
只显示原始数据点,未进行分组标记
-
添加了问题描述,让用户可以自己观察并分组
-
保存为"商场客户原始数据散点图.png"
-
二、认识今天的主角:k-均值聚类
2.1 "物以类聚"的机器版本
聚类,简单来说就是"物以类聚,人以群分"的机器实现。机器在没有老师指导(无标签)的情况下,自己发现数据中的"小团体"。
监督学习 vs 无监督学习:
-
监督学习:像做有答案的习题(有标签)
-
无监督学习:像自己整理杂乱的书架(无标签)
2.2 一个小思考题
想象你有这些水果,如何按"甜度"和"水分"给它们分组?
这里我使用python语言制作了如下的图片:
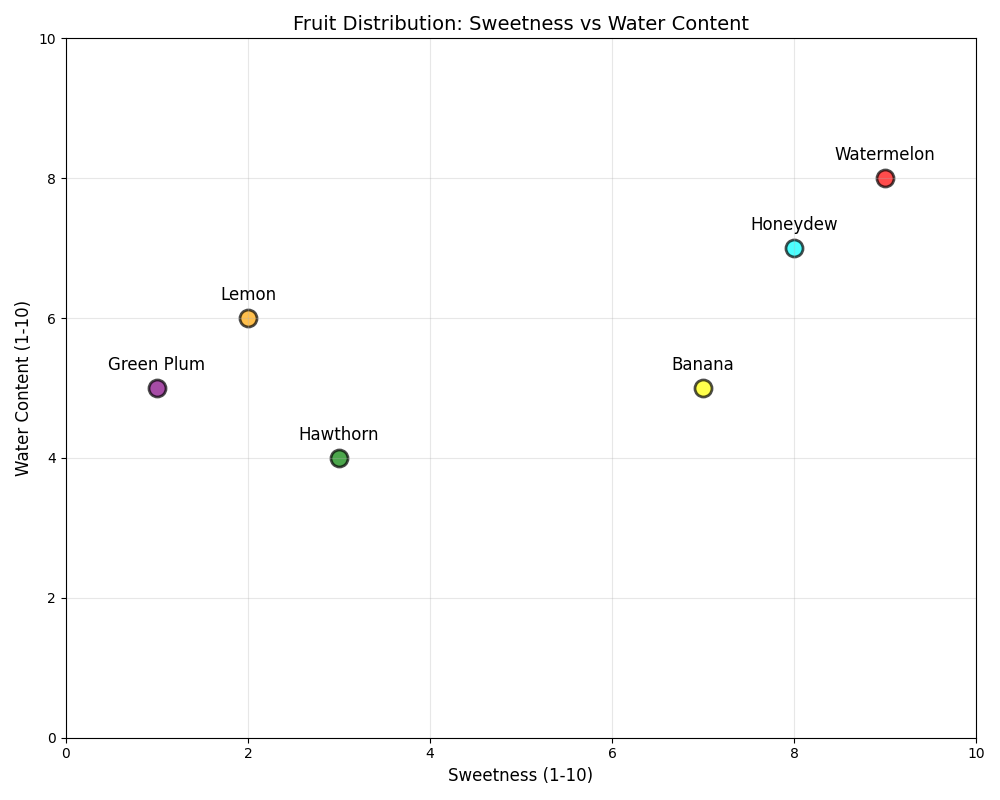
想一想:
-
你能发现几类水果?
-
你的分类标准是什么?
-
如果让你画线分开它们,怎么画?
这里是这张图片的python代码:
python
import matplotlib.pyplot as plt
import numpy as np
# 水果数据 [甜度, 水分],分值1-10
fruit_data = {
'Watermelon': [9, 8], # 很甜,多水分
'Lemon': [2, 6], # 很酸,多水分
'Banana': [7, 5], # 较甜,少水分
'Hawthorn': [3, 4], # 很酸,少水分
'Honeydew': [8, 7], # 很甜,多水分
'Green Plum': [1, 5] # 极酸,多水分
}
# 提取数据
fruit_names = list(fruit_data.keys())
sweetness = [fruit_data[fruit][0] for fruit in fruit_names]
water_content = [fruit_data[fruit][1] for fruit in fruit_names]
# 创建图形
plt.figure(figsize=(10, 8))
# 绘制散点图,用不同颜色区分
colors = ['red', 'orange', 'yellow', 'green', 'cyan', 'purple']
for i, (fruit, x, y) in enumerate(zip(fruit_names, sweetness, water_content)):
plt.scatter(x, y, color=colors[i], s=150, alpha=0.7, edgecolors='black', linewidth=2)
plt.text(x, y+0.2, fruit, fontsize=12, ha='center', va='bottom')
# 设置坐标轴标签
plt.xlabel('Sweetness (1-10)', fontsize=12)
plt.ylabel('Water Content (1-10)', fontsize=12)
plt.title('Fruit Distribution: Sweetness vs Water Content', fontsize=14)
# 设置坐标轴范围
plt.xlim(0, 10)
plt.ylim(0, 10)
# 添加网格
plt.grid(True, alpha=0.3)
# 显示图形
plt.tight_layout()
plt.show()三、K-均值算法:四步"舞蹈"轻松学
3.1 核心比喻:选班干部!
K-均值的过程就像班级选班干部:
-
随机提名:先随机选K个班长候选人(初始质心)
-
投票归属:每个同学投票给离自己最近的班长(分配点到最近质心)
-
重新计票:根据投票结果,重新计算每个班长应该站的位置(更新质心)
-
重复投票:直到班长位置不再变化(算法收敛)
3.2 详细四步曲
|--------|-----------|--------------|--------------|
| 步骤 | 算法做什么 | 生活比喻 | 数学简化 |
| 1. 初始化 | 随机选K个质心 | 随便拿3个衣架挂不同衣服 | 在数据范围内随机选K个点 |
| 2. 分配 | 每个点找最近质心 | 每件衣服挂到最近的衣架 | 勾股定理 |
| 3. 更新 | 重新计算质心位置 | 调整衣架到衣服堆的中心 | 求平均值 |
| 4. 判断 | 质心还变吗? | 衣架位置稳定了吗? | 距离<阈值就停止 |
关键概念:
-
距离计算:就是中学学的"两点间距离公式"
-
质心:就是一个簇所有点的"平均位置"
-
K值:你想把数据分成几类(就像决定选几个班长)
3.3 算法的"性格特点"
三大优点:
-
收敛快:通常几次迭代就稳定
-
实现简单:核心思想容易理解
-
计算高效:适合大规模数据
四个局限:
-
需要指定K:你得提前知道(或猜)分几类
-
对初始点敏感:不同的随机起点可能得到不同结果
-
只找圆形簇:数据如果是其他形状(如月牙形)就不好分了
-
怕异常值:一个极端值可能带偏整个簇
四、动手实践:亲眼看见聚类发生
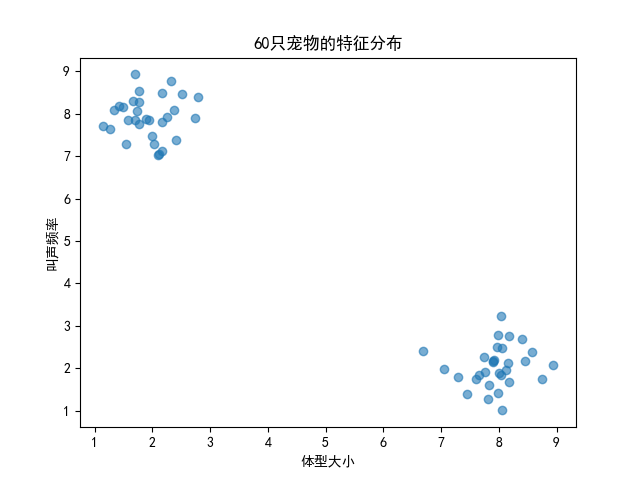
4.1 准备数据:60只"宠物"的特征
我们创建一个有趣的数据集:60只宠物,用"体型大小"和"叫声频率"两个特征来描述。
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import matplotlib
# 设置中文字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
matplotlib.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 创建数据集
np.random.seed(42)
# 30只小猫:体型小(2),叫声频率高(8)
小猫 = np.random.randn(30, 2) * 0.5 + [2, 8]
# 30只小狗:体型大(8),叫声频率低(2)
小狗 = np.random.randn(30, 2) * 0.5 + [8, 2]
# 合并数据
X = np.vstack([小猫, 小狗])
# 先看看数据长什么样
plt.scatter(X[:,0], X[:,1], alpha=0.6)
plt.xlabel("体型大小")
plt.ylabel("叫声频率")
plt.title("60只宠物的特征分布")
plt.show()运行后你会看到:点明显分成了左上和右下两团
4.2 第一次聚类:分出"猫"和"狗"
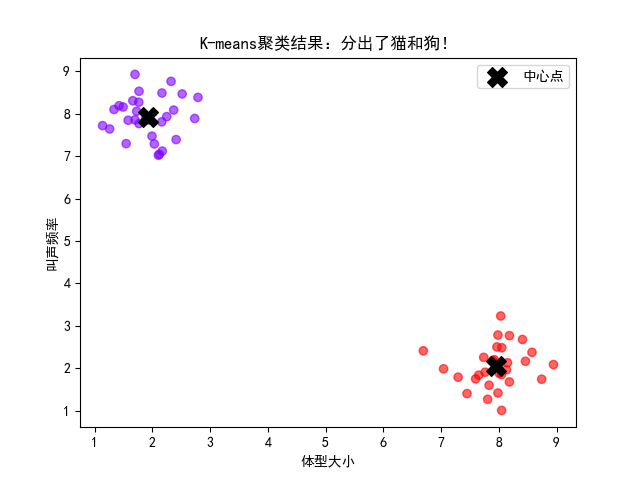
观察与思考:
-
算法真的分出了两簇吗?
-
中心点大约在什么位置?(应该在[2,8]和[8,2]附近)
-
有没有"分错"的点?为什么会有?
此处代码:
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import matplotlib
# 设置中文字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
matplotlib.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 创建数据集
np.random.seed(42)
# 30只小猫:体型小(2),叫声频率高(8)
小猫 = np.random.randn(30, 2) * 0.5 + [2, 8]
# 30只小狗:体型大(8),叫声频率低(2)
小狗 = np.random.randn(30, 2) * 0.5 + [8, 2]
# 合并数据
X = np.vstack([小猫, 小狗])
# 先看看数据长什么样
plt.scatter(X[:,0], X[:,1], alpha=0.6)
plt.xlabel("体型大小")
plt.ylabel("叫声频率")
plt.title("60只宠物的特征分布")
plt.show()
# 最简单的三行代码完成聚类
kmeans = KMeans(n_clusters=2, random_state=42) # 告诉算法:我想分2类
kmeans.fit(X) # 开始聚类!
# 看看结果
labels = kmeans.labels_ # 每个点的标签:0或1
centers = kmeans.cluster_centers_ # 两个簇的中心点
print("前10个点的标签:", labels[:10])
print("\n两个簇的中心坐标:")
print("中心1(可能是猫):", centers[0])
print("中心2(可能是狗):", centers[1])
# 可视化结果
plt.scatter(X[:,0], X[:,1], c=labels, cmap='rainbow', alpha=0.6)
plt.scatter(centers[:,0], centers[:,1],
c='black', s=200, marker='X', label='中心点')
plt.xlabel("体型大小")
plt.ylabel("叫声频率")
plt.title("K-means聚类结果:分出了猫和狗!")
plt.legend()
plt.show()4.3 K值的影响:分几类最合适?
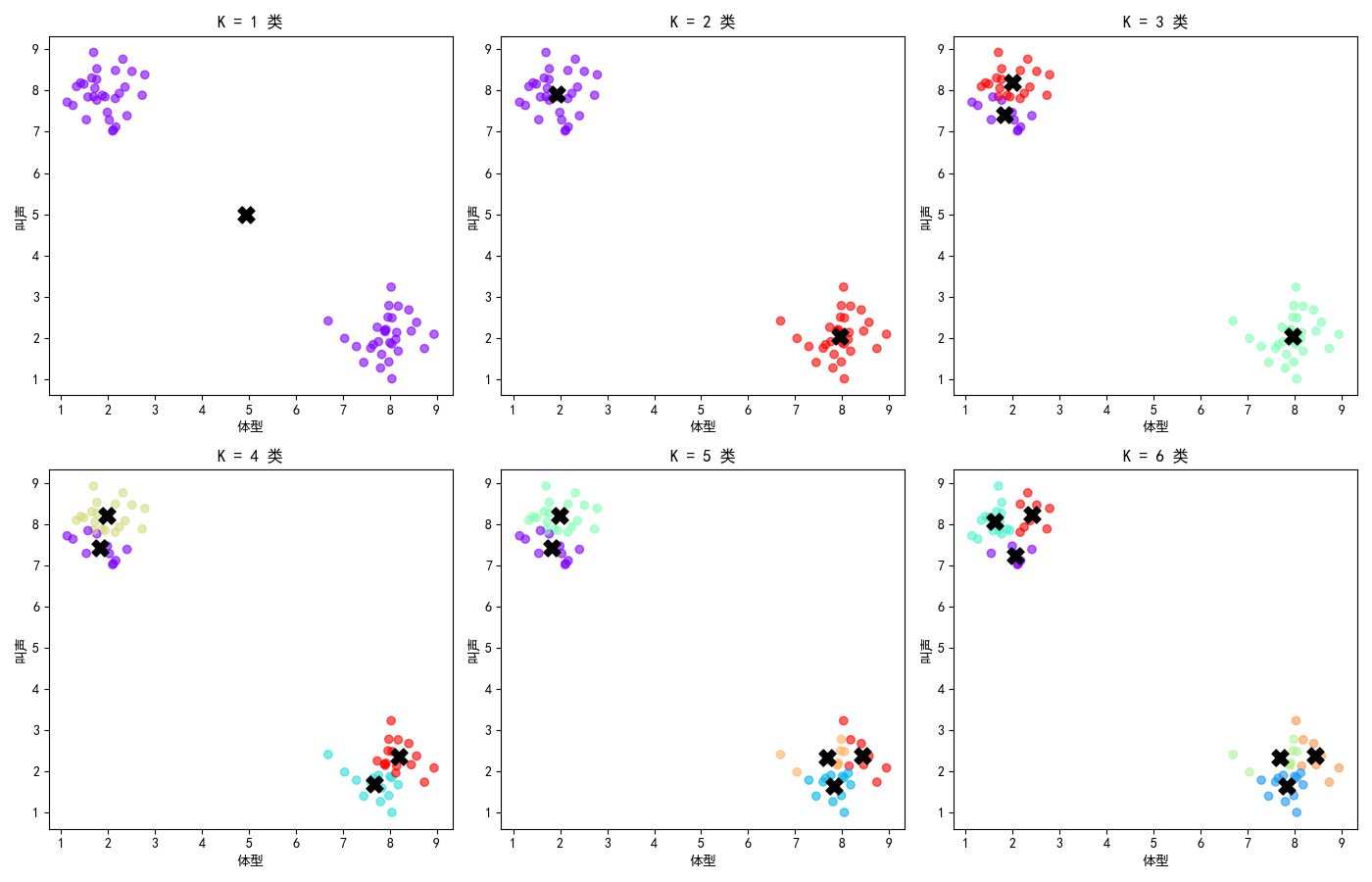
如果我们改变K值(想分的类数),会发生什么?
关键发现:
-
K=1:所有点都是同一类 → 这没意义
-
K=2:完美分出了猫和狗 → 这正是我们想要的!
-
K=3,4,5...:开始"过度细分",硬把一簇拆成多簇
-
K=6:几乎每个点都快自成一类了 → 太过分了!
此处所使用到的代码:
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import matplotlib
# 设置中文字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
matplotlib.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 创建数据集
np.random.seed(42)
# 30只小猫:体型小(2),叫声频率高(8)
小猫 = np.random.randn(30, 2) * 0.5 + [2, 8]
# 30只小狗:体型大(8),叫声频率低(2)
小狗 = np.random.randn(30, 2) * 0.5 + [8, 2]
# 合并数据
X = np.vstack([小猫, 小狗])
# 先看看数据长什么样
plt.scatter(X[:,0], X[:,1], alpha=0.6)
plt.xlabel("体型大小")
plt.ylabel("叫声频率")
plt.title("60只宠物的特征分布")
plt.show()
# 最简单的三行代码完成聚类
kmeans = KMeans(n_clusters=2, random_state=42) # 告诉算法:我想分2类
kmeans.fit(X) # 开始聚类!
# 看看结果
labels = kmeans.labels_ # 每个点的标签:0或1
centers = kmeans.cluster_centers_ # 两个簇的中心点
print("前10个点的标签:", labels[:10])
print("\n两个簇的中心坐标:")
print("中心1(可能是猫):", centers[0])
print("中心2(可能是狗):", centers[1])
# 可视化结果
plt.scatter(X[:,0], X[:,1], c=labels, cmap='rainbow', alpha=0.6)
plt.scatter(centers[:,0], centers[:,1],
c='black', s=200, marker='X', label='中心点')
plt.xlabel("体型大小")
plt.ylabel("叫声频率")
plt.title("K-means聚类结果:分出了猫和狗!")
plt.legend()
plt.show()
# 试试不同的K值:从1到6
fig, axes = plt.subplots(2, 3, figsize=(14, 9))
for k, ax in zip([1, 2, 3, 4, 5, 6], axes.ravel()):
# 每次用不同的K
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
# 画图
ax.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap='rainbow', alpha=0.6)
ax.scatter(kmeans.cluster_centers_[:, 0],
kmeans.cluster_centers_[:, 1],
c='black', s=150, marker='X')
ax.set_title(f'K = {k} 类')
ax.set_xlabel("体型")
ax.set_ylabel("叫声")
plt.tight_layout()
plt.show()4.4 如何科学选择K值?肘部法则来帮忙!
我们不想瞎猜K值,有没有科学方法?有!就是肘部法则。
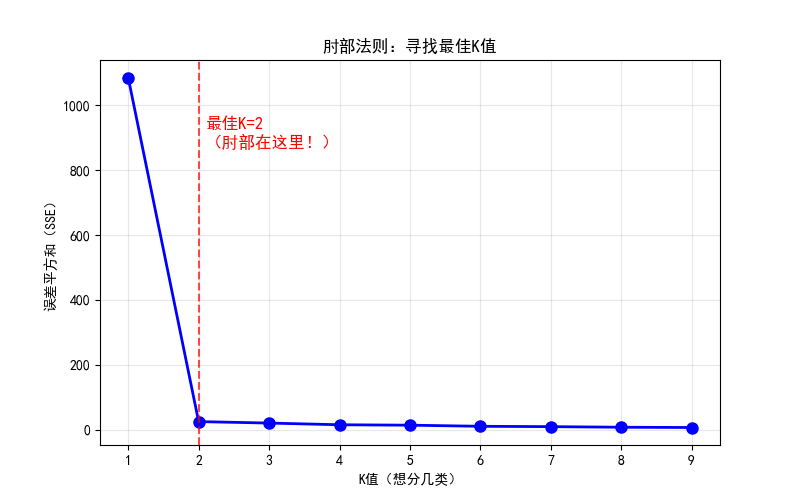
肘部法则的直观解释:
-
误差(SSE):可以理解为"不满意度"
-
K太小(如K=1):大家挤在一起,很不满意 → 误差大
-
K合适(如K=2):各自找到组织,满意度高 → 误差明显下降
-
K太大(如K>3):过度管理,性价比低 → 误差下降变慢
-
"肘部":就是那个拐点,性价比最高的K值!
此处使用到的代码:
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import matplotlib
# 设置中文字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
matplotlib.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 创建数据集
np.random.seed(42)
# 30只小猫:体型小(2),叫声频率高(8)
小猫 = np.random.randn(30, 2) * 0.5 + [2, 8]
# 30只小狗:体型大(8),叫声频率低(2)
小狗 = np.random.randn(30, 2) * 0.5 + [8, 2]
# 合并数据
X = np.vstack([小猫, 小狗])
# 先看看数据长什么样
plt.scatter(X[:,0], X[:,1], alpha=0.6)
plt.xlabel("体型大小")
plt.ylabel("叫声频率")
plt.title("60只宠物的特征分布")
plt.show()
# 最简单的三行代码完成聚类
kmeans = KMeans(n_clusters=2, random_state=42) # 告诉算法:我想分2类
kmeans.fit(X) # 开始聚类!
# 看看结果
labels = kmeans.labels_ # 每个点的标签:0或1
centers = kmeans.cluster_centers_ # 两个簇的中心点
print("前10个点的标签:", labels[:10])
print("\n两个簇的中心坐标:")
print("中心1(可能是猫):", centers[0])
print("中心2(可能是狗):", centers[1])
# 可视化结果
plt.scatter(X[:,0], X[:,1], c=labels, cmap='rainbow', alpha=0.6)
plt.scatter(centers[:,0], centers[:,1],
c='black', s=200, marker='X', label='中心点')
plt.xlabel("体型大小")
plt.ylabel("叫声频率")
plt.title("K-means聚类结果:分出了猫和狗!")
plt.legend()
plt.show()
# 试试不同的K值:从1到6
fig, axes = plt.subplots(2, 3, figsize=(14, 9))
for k, ax in zip([1, 2, 3, 4, 5, 6], axes.ravel()):
# 每次用不同的K
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
# 画图
ax.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap='rainbow', alpha=0.6)
ax.scatter(kmeans.cluster_centers_[:, 0],
kmeans.cluster_centers_[:, 1],
c='black', s=150, marker='X')
ax.set_title(f'K = {k} 类')
ax.set_xlabel("体型")
ax.set_ylabel("叫声")
plt.tight_layout()
plt.show()
# 计算不同K值时的"误差"
inertias = []
K_range = range(1, 10) # 试试K从1到9
for k in K_range:
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
inertias.append(kmeans.inertia_) # 误差平方和(SSE)
# 画出"误差-K值"曲线
plt.figure(figsize=(8, 5))
plt.plot(K_range, inertias, 'bo-', linewidth=2, markersize=8)
plt.xlabel('K值(想分几类)')
plt.ylabel('误差平方和(SSE)')
plt.title('肘部法则:寻找最佳K值')
plt.grid(True, alpha=0.3)
# 标记肘部
plt.axvline(x=2, color='r', linestyle='--', alpha=0.7)
plt.text(2.1, max(inertias)*0.8, '最佳K=2\n(肘部在这里!)',
color='red', fontsize=12, fontweight='bold')
plt.show()五、真实应用:K-均值在改变世界
5.1 你身边的聚类应用
|----------|---------------|-----------------------|
| 应用场景 | 数据是什么 | 聚类目的 |
| 电商推荐 | 你的购买记录、浏览时间 | 把相似用户聚在一起,给你推荐他们喜欢的东西 |
| 新闻分类 | 文章关键词、TF-IDF值 | 自动发现热点话题,整理新闻 |
| 图像压缩 | 图片所有像素的RGB颜色值 | 提取主要颜色,减少颜色数量(颜色量化) |
| 异常检测 | 服务器访问日志、交易记录 | 发现异常模式(如黑客攻击、信用卡欺诈) |
5.2 小挑战:找出"异常学生"
给你一些学生数据:[学习时间, 考试成绩],你能找出异常者吗?
下面是我使用Python画出的一些图片:
第一张图片:"异常学生检测结果.png"(包含三个子图)
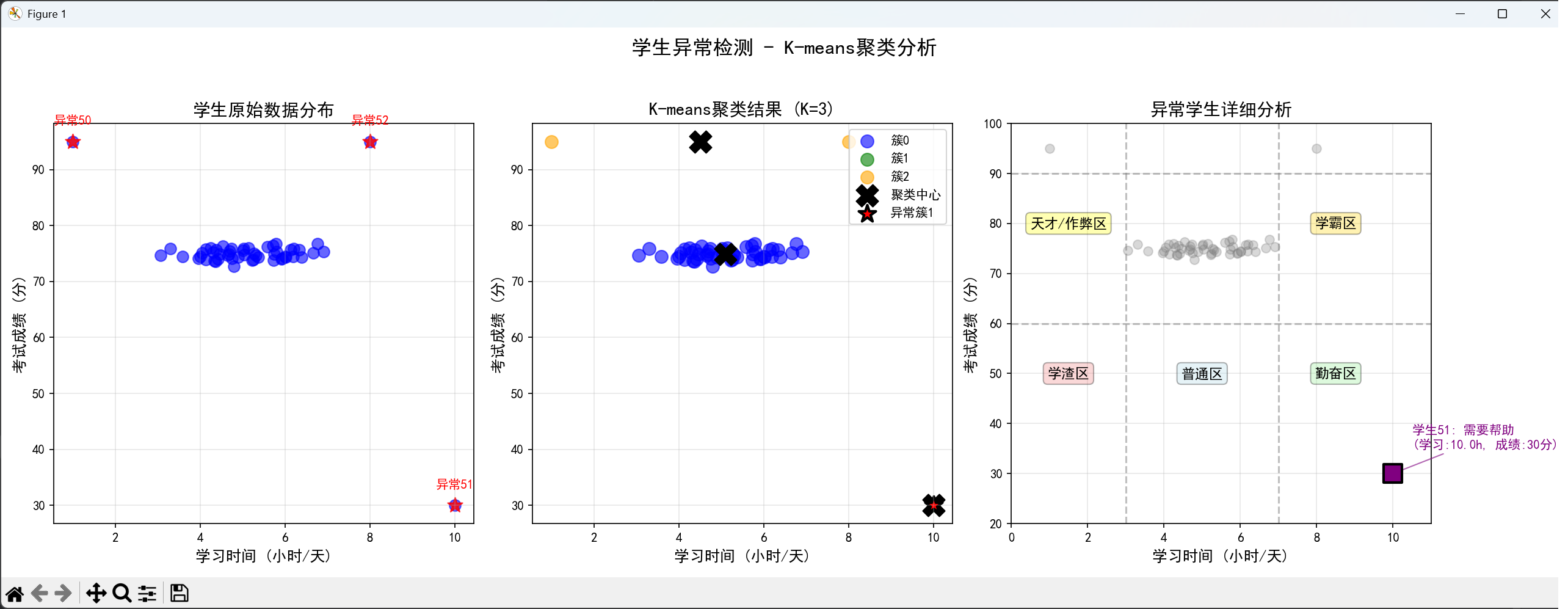
左子图:学生原始数据分布图
展示了53名学生的原始特征分布,横轴为学习时间(小时/天),纵轴为考试成绩(分)。图中大部分蓝色点集中在中部区域(学习时间4-6小时,成绩70-80分),代表正常学生群体。三个红色星号标记了预设的异常学生位置:左上角(学习时间极少但成绩极高)、右下角(学习时间极长但成绩极低)、右上角(学习时间长且成绩高)。这张图直观呈现了数据的基本结构和异常点的明显偏离特征,为后续聚类分析奠定了视觉基础。
中子图:K-means聚类结果图
展示了K-means算法(K=3)的聚类效果。不同颜色(蓝、绿、橙)代表三个不同的簇,黑色"X"标记表示各簇的质心。值得注意的是,红色星号标记的异常学生全部被分到了橙色簇中,形成了一个独立的异常簇。该簇的质心明显偏离正常学生簇的质心,表明算法成功捕捉到了数据的异常模式。图中还清晰展示了正常学生被分为两个簇的情况,反映了学生群体中可能存在的亚群体差异。
右子图:异常学生详细分析图
提供了对异常学生的深度分析。通过灰色背景点表示正常学生,用不同形状和颜色的标记突出三名异常学生,并为每个异常学生添加了详细的文字标注(包括学生编号、异常类型、具体数据)。图中添加了参考网格线(学习时间3小时和7小时分界线,成绩60分和90分分界线)和五个特征区域标注(学渣区、普通区、勤奋区、天才/作弊区、学霸区),帮助理解异常学生相对于正常范围的偏离程度。这张图不仅识别了异常学生,还对其异常类型进行了智能分类和解释。
第二张图片:"肘部法则分析.png"
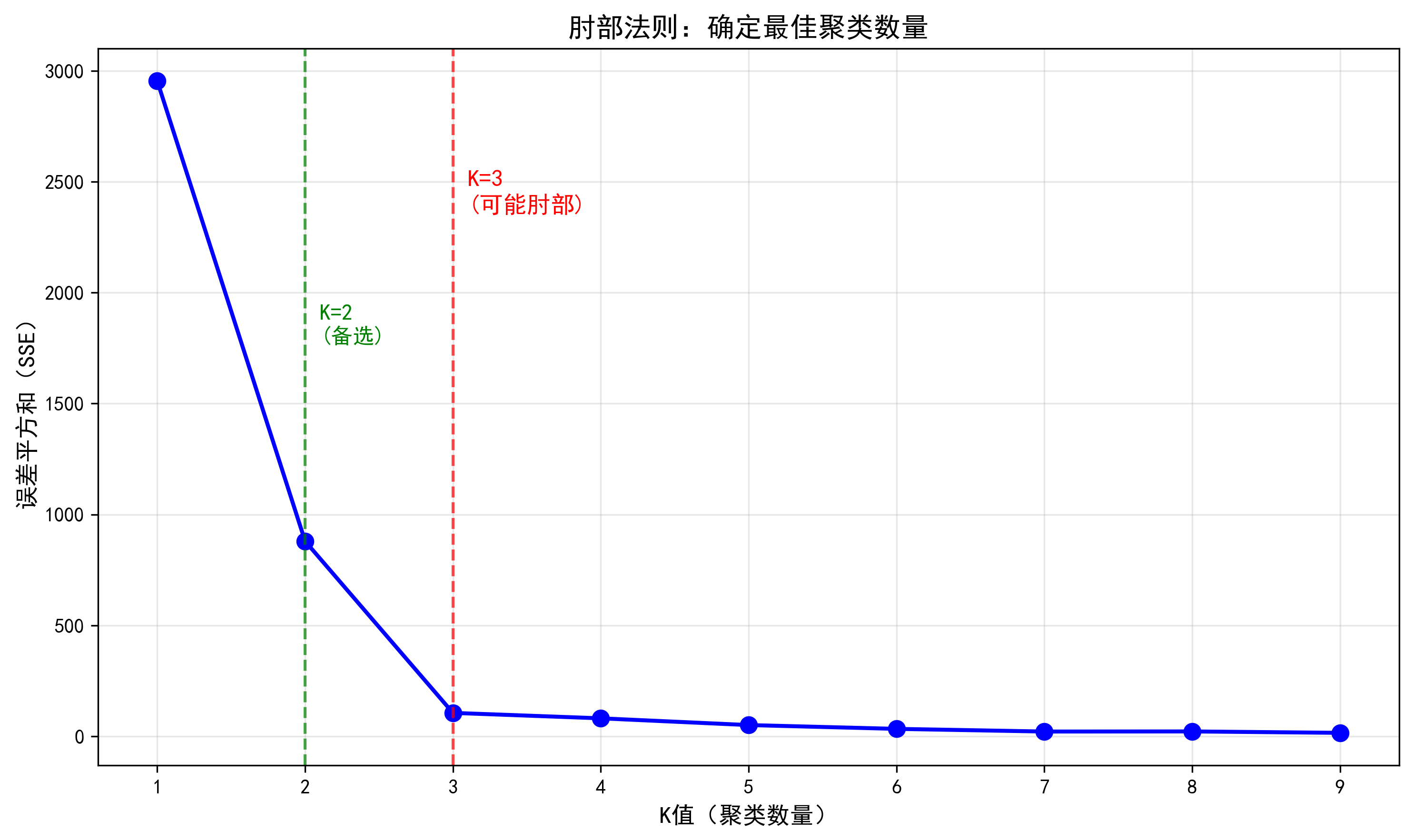
这张图运用肘部法则来验证K值选择的科学性。横轴表示不同的K值(从1到9),纵轴表示对应的误差平方和(SSE)。蓝色点线显示了SSE随K值增加而下降的趋势:当K从1增加到3时,SSE急剧下降;当K大于3后,SSE下降速度明显变缓。图中用红色虚线标出了K=3的位置,并标注为"可能肘部",表明此处是曲线的拐点,增加更多簇带来的收益显著降低。这张图为选择K=3提供了数据支持,避免了聚类数量选择的主观随意性,体现了机器学习中参数优化的科学方法。
六、总结回顾与进阶思考
6.1 三句话掌握K-均值
-
是什么:让机器自己发现数据中的"小团体"
-
怎么做:选班长 → 投票 → 调整位置 → 重新投票(直到稳定)
-
何时用:当你不知道数据有哪些类别,但相信"相似的总会聚在一起"
6.2 给你的小任务
打开你的音乐播放列表(或任何你有数据的地方),尝试:
-
找2-3个特征(如节奏快慢、音量大小、歌曲时长)
-
用K-均值分成3-4类
-
看看机器分的类,和你自己感觉的类别一致吗?
6.3 鼓励的话
今天,你用不到90分钟的时间,掌握了一个真正在工业中使用的机器学习算法。虽然K-均值是最简单的聚类算法之一,但它解决了无数实际问题。
记住:最强大的工具往往源于最简单的思想。聚类的大门已经为你打开,接下来还有层次聚类、DBSCAN、高斯混合模型等更"聪明"的算法等着你探索。
附:完整代码集合
如果你想要一次性运行所有代码,这里提供了一个完整版本:
下面这段代码完整演示了K-means聚类算法的完整工作流程:首先创建了一个模拟的"猫狗数据集"(包含60个宠物样本,每个样本有体型大小和叫声频率两个特征),然后使用K-means算法将数据分为两类(K=2),最后通过"肘部法则"确定最佳聚类数量。整个过程涵盖了数据生成、算法应用、结果可视化和参数优化四个关键环节。
python
# 1. 导入库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# 2. 创建猫狗数据集
np.random.seed(42)
小猫 = np.random.randn(30, 2) * 0.5 + [2, 8]
小狗 = np.random.randn(30, 2) * 0.5 + [8, 2]
X = np.vstack([小猫, 小狗])
# 3. 执行聚类(K=2)
kmeans = KMeans(n_clusters=2, random_state=42)
kmeans.fit(X)
# 4. 可视化结果
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.scatter(X[:,0], X[:,1], alpha=0.6)
plt.title("原始数据")
plt.xlabel("体型大小"); plt.ylabel("叫声频率")
plt.subplot(1, 2, 2)
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_, cmap='rainbow', alpha=0.6)
plt.scatter(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1],
c='black', s=200, marker='X')
plt.title("K-means聚类结果 (K=2)")
plt.xlabel("体型大小"); plt.ylabel("叫声频率")
plt.tight_layout()
plt.show()
# 5. 肘部法则
inertias = []
for k in range(1, 10):
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
inertias.append(kmeans.inertia_)
plt.figure(figsize=(8, 4))
plt.plot(range(1, 10), inertias, 'bo-')
plt.xlabel('K值'); plt.ylabel('误差平方和')
plt.title('肘部法则:最佳K=2')
plt.axvline(x=2, color='r', linestyle='--')
plt.grid(True, alpha=0.3)
plt.show()第一张图片:原始数据与聚类结果对比图(包含两个子图)
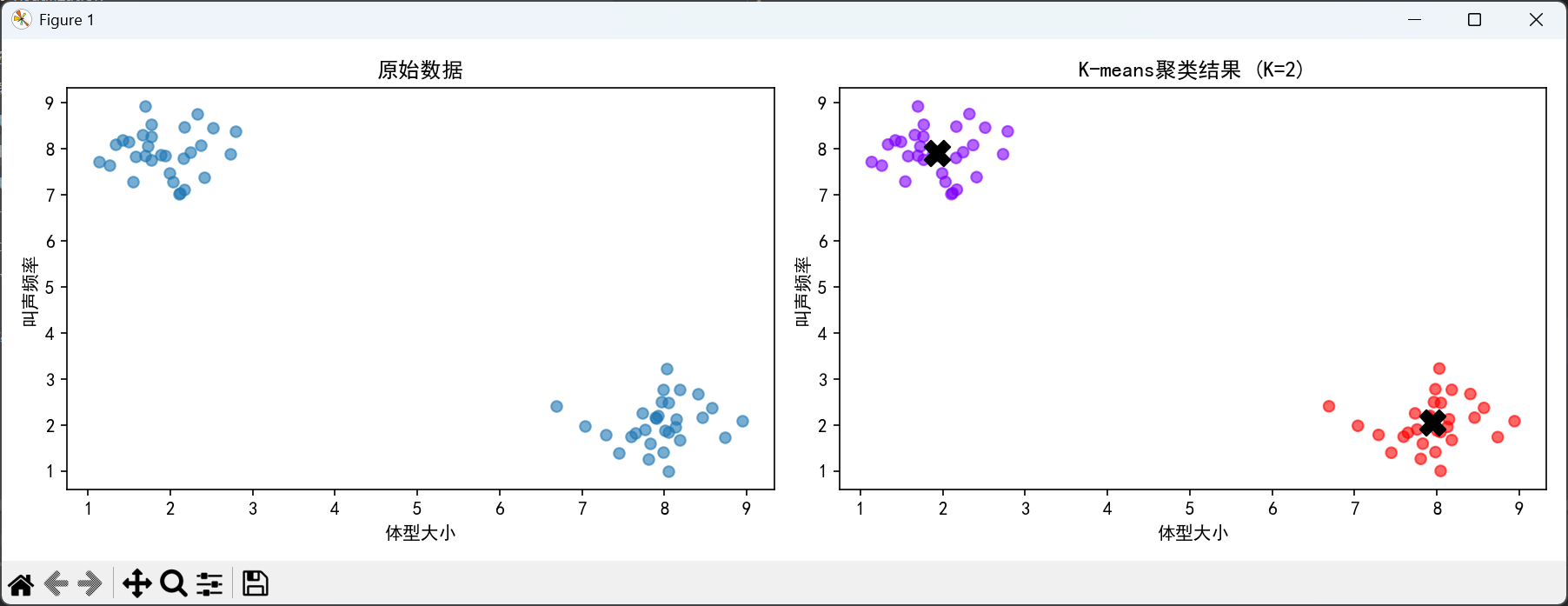
左侧子图(原始数据分布) :
展示了60只宠物的原始特征分布,横轴表示体型大小,纵轴表示叫声频率。图中可以明显看到数据点自然分成两个区域:左上角区域(体型小、叫声频率高,代表小猫)和右下角区域(体型大、叫声频率低,代表小狗)。这张图直观呈现了数据的自然分组结构,为后续聚类分析提供了视觉基础。
右侧子图(K-means聚类结果) :
展示了K-means算法(K=2)的聚类结果。相同颜色的点属于同一簇,黑色"X"标记表示每个簇的质心(中心点)。从图中可以看到,算法成功将数据分成了两个簇,基本对应了猫和狗的自然分类。质心位置分别位于每个簇的中心,这表明算法找到了数据的内在分组结构。
第二张图片:肘部法则图
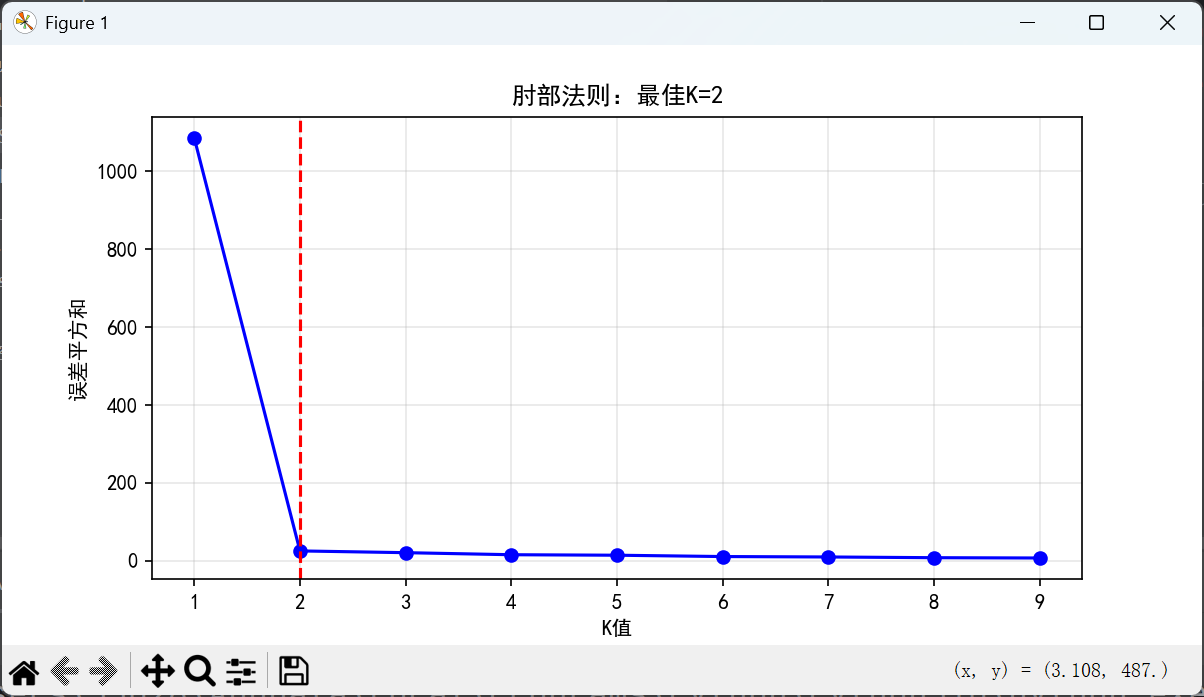
展示了"肘部法则"用于确定最佳K值的过程。横轴表示不同的K值(从1到9),纵轴表示对应的误差平方和(SSE)。图中用蓝色点线连接了每个K值对应的SSE值,红色虚线标记了K=2的位置。曲线在K=2处出现明显的拐点(形似"肘部"),之后SSE的下降趋势明显变缓,这表明K=2是最具"性价比"的聚类数量,增加更多簇的收益有限。这张图形象展示了如何科学地选择聚类数量,避免主观猜测。