探索八索并联绳索机器人的Matlab仿真模型

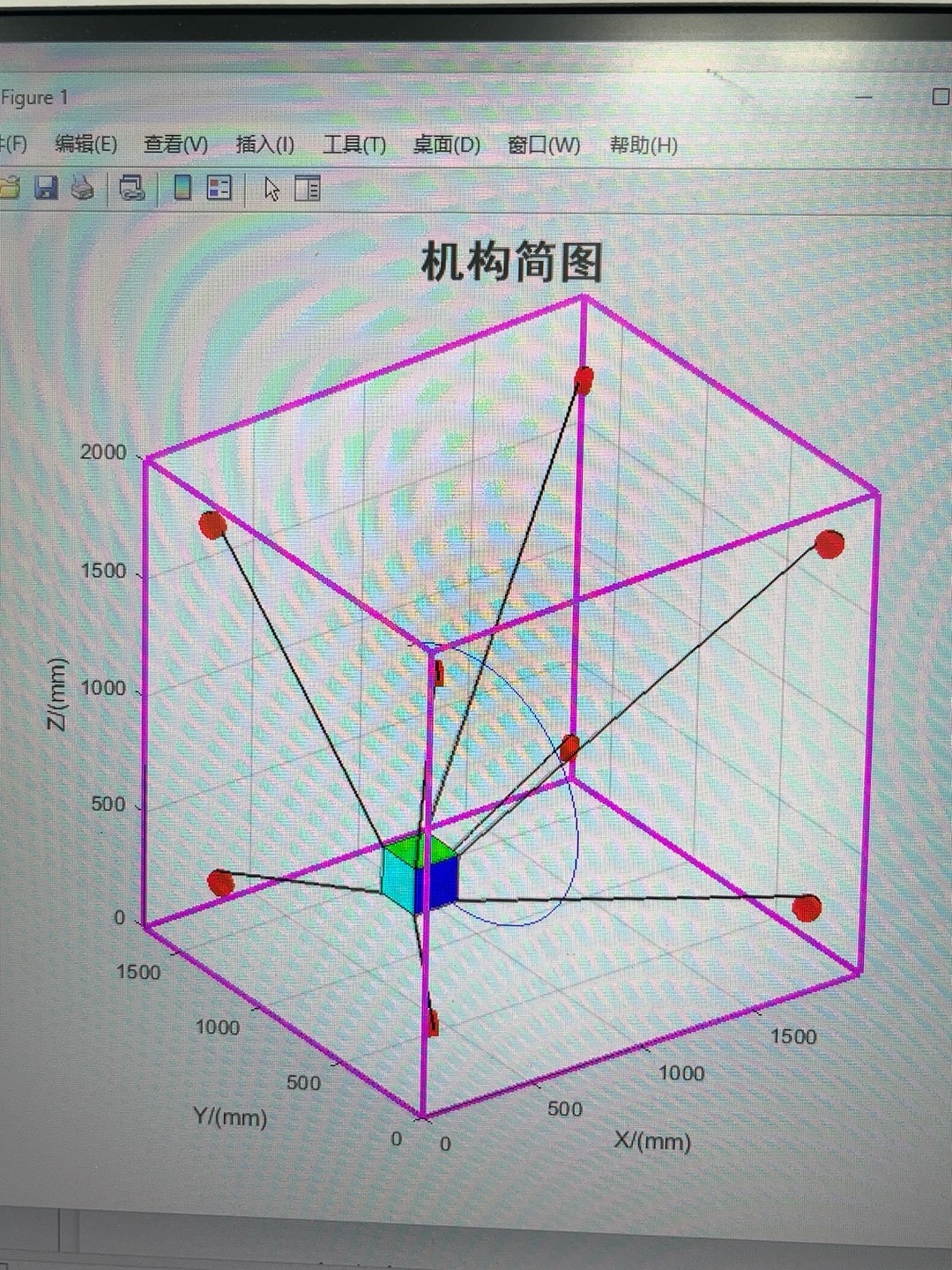
八索并联绳索机器人仿真matlab模型，带出绳点滑轮摆动与俯仰，是运动学模型另外还有正运动学模型，力分配以及动力学模型，可以改

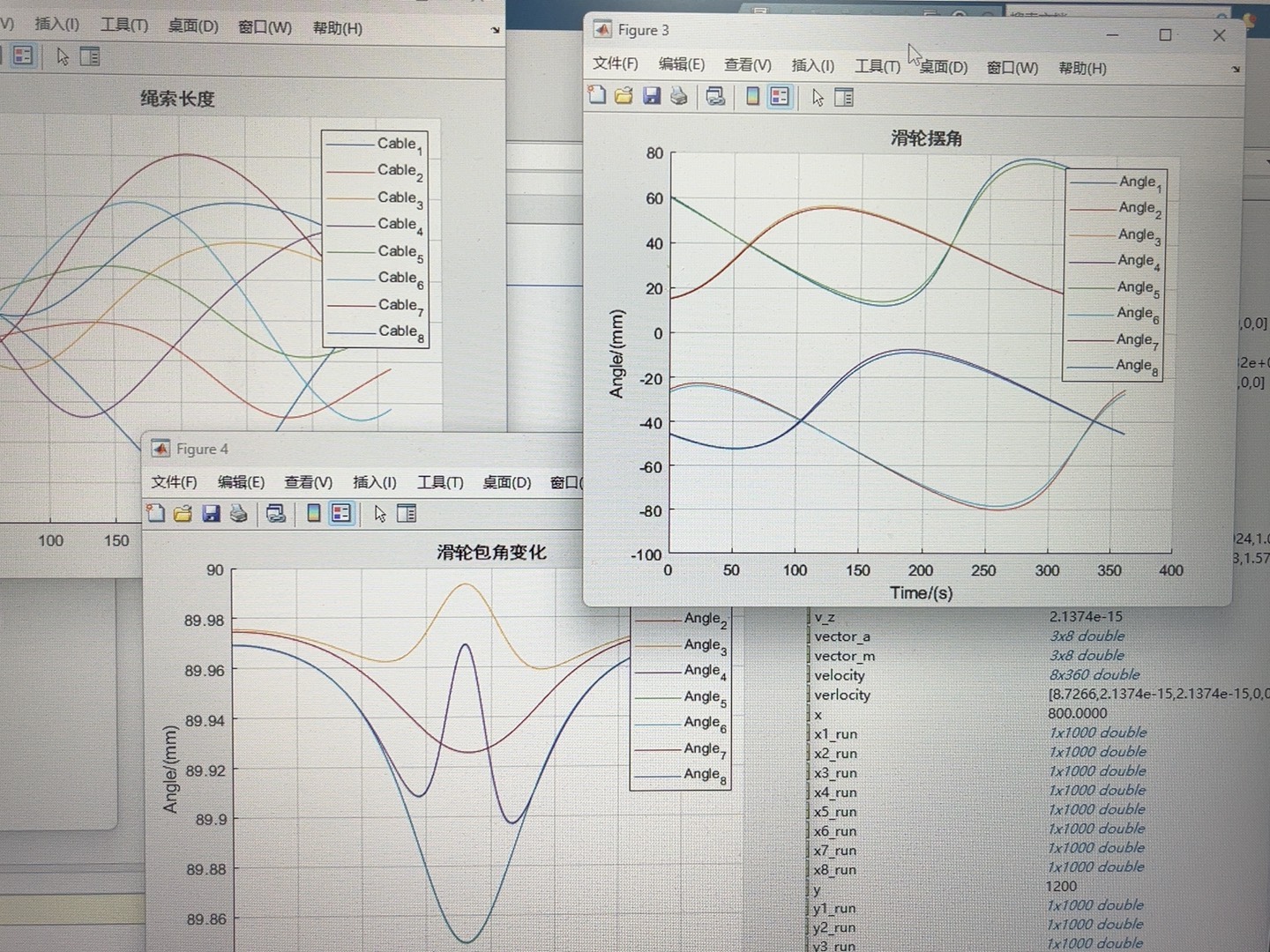
最近在研究八索并联绳索机器人，发现它的Matlab仿真模型真是个有趣又充满挑战的领域。今天就来和大家唠唠其中涉及的一些关键模型。

带出绳点滑轮摆动与俯仰的运动学模型

这部分模型主要聚焦在机器人的带出绳点滑轮的运动特性上。想象一下，滑轮的摆动和俯仰动作对于机器人整体的运行有着至关重要的影响。在Matlab里，我们可以通过定义一些基本的几何参数和运动方程来构建这个模型。

matlab 复制代码

% 定义初始参数
l1 = 1; % 某个连杆长度
theta1 = pi/4; % 初始角度

% 计算位置
x = l1 * cos(theta1);
y = l1 * sin(theta1);

在这段简单代码里，我们先定义了一个连杆长度 l1 和初始角度 theta1 ，通过三角函数计算出在这个角度下，对应点在平面坐标系中的 x 和 y 坐标。这只是运动学模型里非常基础的一个示例，实际的带出绳点滑轮摆动与俯仰运动学模型会复杂得多，可能涉及到多个关节、角度和空间坐标的变换。

正运动学模型

正运动学模型旨在根据给定的机器人关节输入参数，计算出末端执行器的位置和姿态。简单理解就是，知道机器人各个关节怎么动，推测出它的"手"会到哪里。

matlab 复制代码

% 假设机器人有3个关节，定义关节角度
q1 = pi/6;
q2 = pi/3;
q3 = pi/4;

% 定义连杆长度
a1 = 1;
a2 = 1;
a3 = 1;

% 计算末端执行器位置（这里是简化的2D示例）
x_end = a1 * cos(q1) + a2 * cos(q1 + q2) + a3 * cos(q1 + q2 + q3);
y_end = a1 * sin(q1) + a2 * sin(q1 + q2) + a3 * sin(q1 + q2 + q3);

这段代码通过给定三个关节角度 q1、q2、q3 以及连杆长度 a1、a2、a3 ，利用三角函数来计算末端执行器在二维平面上的位置 xend**和 y end 。实际的八索并联绳索机器人正运动学模型，会基于更复杂的空间几何和矩阵变换，因为它要考虑到绳索的布局和空间中各个方向的运动。

力分配模型

力分配模型关乎如何合理地将机器人所需的合力分配到每一根绳索上。毕竟八根绳索协同工作，力的分配不当，机器人可能就"站不稳"或者"运动不协调"。

matlab 复制代码

% 假设已知合力F_total
F_total = [10; 5]; % 二维力向量

% 绳索数量
n = 8;

% 初始化力分配向量
F_distribution = zeros(n, 1);

% 简单的力分配算法示例（这里只是示例，实际更复杂）
for i = 1:n
    F_distribution(i) = F_total(1) / n + randn * 0.1; % 加入一些随机扰动模拟实际情况
end

这里我们先假设有一个已知的合力 Ftotal*，初始化了一个用于存储力分配结果的向量 F* distribution 。通过一个简单的循环，将合力大致平均分配到每根绳索上，并加入一些随机扰动来模拟实际可能出现的情况。真实的力分配模型需要考虑绳索的张力限制、机器人的姿态稳定性等诸多因素，算法会更加复杂精妙。

动力学模型

动力学模型则是研究机器人在力和力矩作用下的运动变化，也就是从力如何转化为运动这个角度去建模。

matlab 复制代码

% 定义质量矩阵M
M = [5 0; 0 5];

% 定义科里奥利力和离心力矩阵C
C = [0 0; 0 0];

% 定义重力向量g
g = [0; -9.8];

% 定义关节力矩tau
tau = [10; 10];

% 动力学方程示例（简化的线性模型）
q_ddot = M \ (tau - C * q_dot - g);

在这段代码里，我们定义了质量矩阵 M 、科里奥利力和离心力矩阵 C 、重力向量 g 以及关节力矩 tau ，通过简单的矩阵运算求解关节的加速度 q_ddot 。八索并联绳索机器人的动力学模型由于绳索的柔性以及多体动力学的耦合特性，会比这个示例复杂得多，需要更精确的力学分析和数学推导。

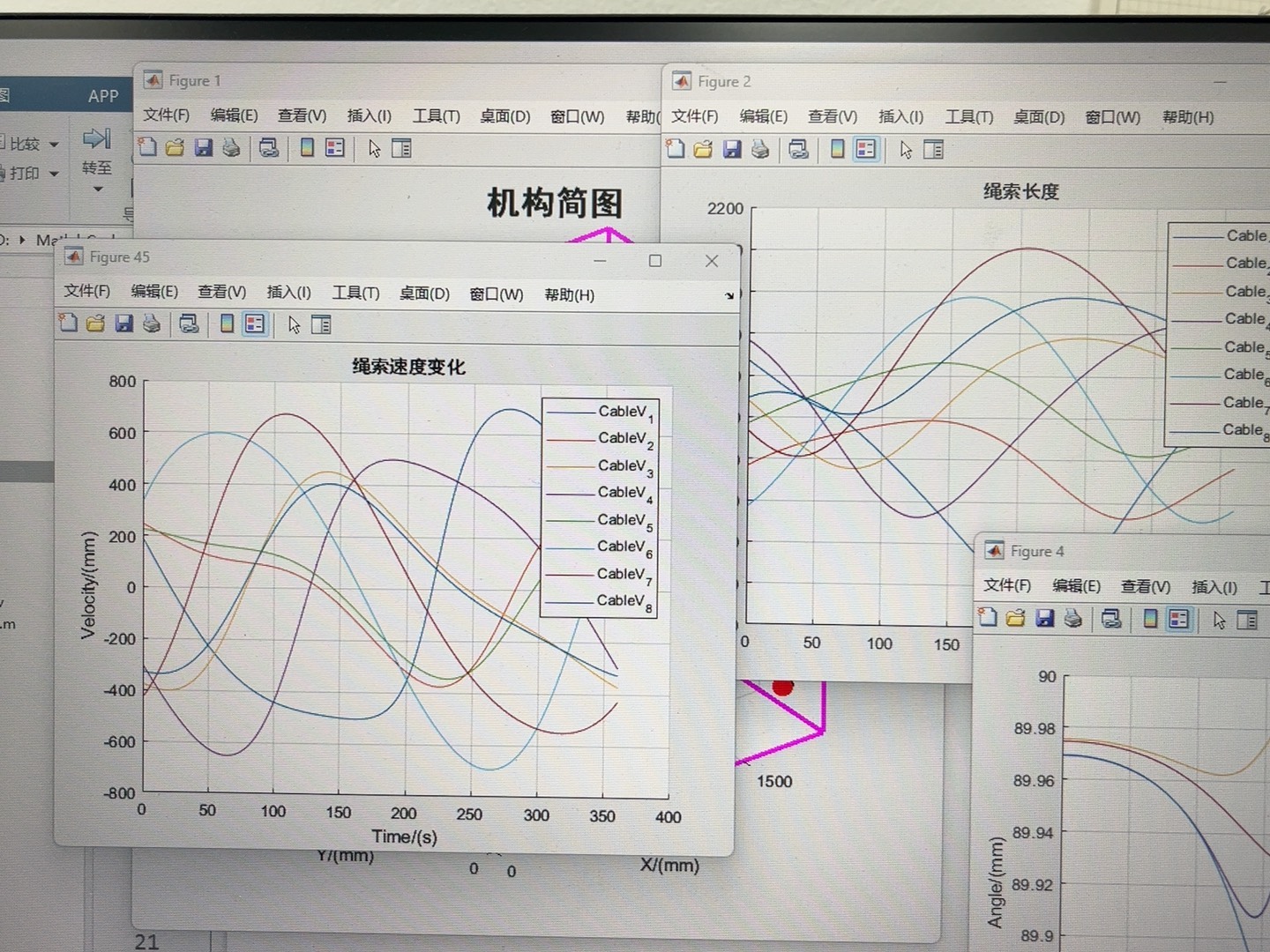
八索并联绳索机器人的这些Matlab仿真模型每一个都充满了研究的乐趣和实际应用价值，它们相互关联，共同为我们构建出一个虚拟的机器人运动模拟环境，无论是对于机器人的设计优化还是控制算法开发都有着举足轻重的作用。后续有更多新发现，再和大家分享！