机器人机械臂建模仿真MATLAB轨迹规划 多项式函数插值/抛物线插值轨迹规划/直线/圆弧轨迹规...

机器人机械臂建模仿真MATLAB轨迹规划 多项式函数插值/抛物线插值轨迹规划/直线/圆弧轨迹规划/3次多项式/5次多项式/B样条等等/353轨迹规划/434轨迹规划，粒子群算法等智能优化算法优化轨迹规划时间

机械臂轨迹规划就像给钢铁手臂编排舞蹈动作，既要避开障碍物，又要动作丝滑不抽风。在MATLAB里折腾过轨迹规划的老铁都知道，这玩意儿看着高大上，实操起来全是细节坑。

三次多项式：直男式插值法

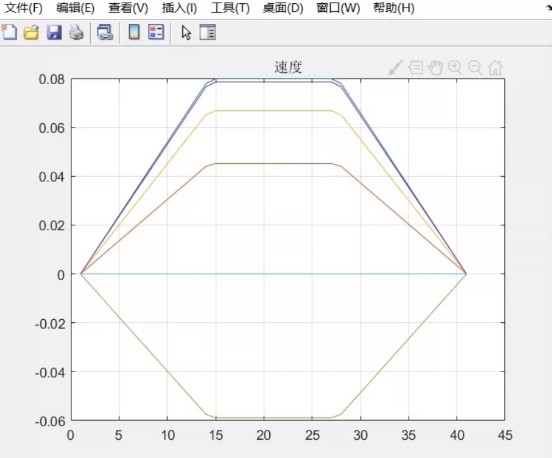
最简单的三次多项式轨迹，适合关节空间规划。假设机械臂从0°到90°转5秒，咱们用polyfit搞个系数矩阵：

t = [0 5]; 
theta = [0 90];
vel = [0 0]; % 端点速度设为零
A = [1 0 0 0; 
     0 1 0 0;
     1 5 25 125;
     0 1 10 75];
b = [0; 0; 90; 0];
coeffs = A\b; % 解线性方程组

这段代码的核心在于构造边界条件矩阵。四个方程对应位置和速度约束，最后算出的四次系数其实是三次多项式（这里有个隐藏知识点：MATLAB的polyfit是从高次到低次排列系数）。

五次多项式：强迫症福音

当需要指定加速度连续时，五次多项式就派上用场了。在笛卡尔空间规划中特别实用：

syms t;
eqns = [a0 == 0,                  % 初始位置
        a1 + 2*a2*t1 + 3*a3*t1^2 == 0, % 终止速度
        a0 + a1*t2 + a2*t2^2 + a3*t2^3 == 1]; % 终止位置

这种符号运算虽然看着优雅，但实际工程中更推荐用数值解法------毕竟符号计算在复杂场景下能把你电脑卡成PPT。

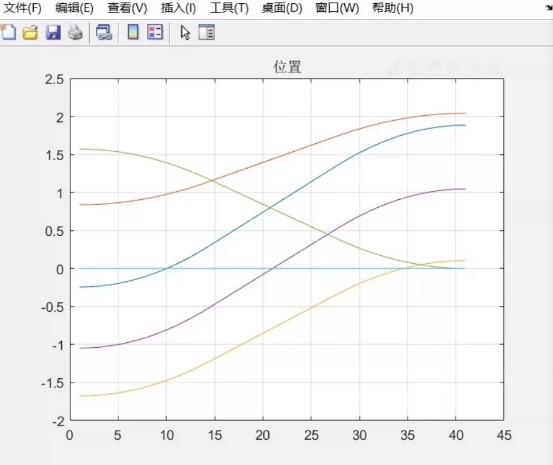
B样条：老司机的选择

想要轨迹柔性高？试试B样条。下面这段代码生成S型速度曲线：

knots = [0 0 0 0 2 4 6 8 8 8 8]; 
cpts = [0 1 3 6 7 8];
sp = spapi(knots, cpts, linspace(0,10,6)); 
fnplt(sp,'r',2)

这里的knot向量设计是精髓：头尾重复度4保证端点插值，中间节点控制曲线形态。不过B样条参数调不好容易翻车，建议配合jerk限制一起使用。

粒子群优化：卷王必备

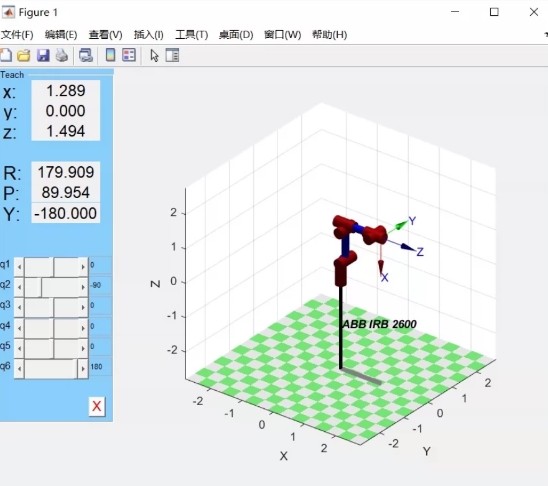
当传统方法搞不定时间最优时，智能算法就该出场了。用粒子群优化轨迹时间：

function time = costFunc(q)
    torque = inverseDynamics(q); % 逆动力学计算
    time = sum(abs(torque)) + 0.5*max(q); % 自定义代价函数
end

options = optimoptions('particleswarm','SwarmSize',50);
[optQ,minTime] = particleswarm(@costFunc, 30, lb, ub, options);

注意代价函数设计要有技巧------直接优化时间可能导致违反动力学约束，这里把力矩消耗和关节位移打包计算。跑一次优化够你喝三杯咖啡，记得先做参数敏感性分析。

轨迹规划没有银弹，三次多项式适合简单搬运作业，B样条用在雕刻这类精细操作，智能算法留着对付甲方奇葩需求。最后提醒：仿真时看着完美的轨迹，上真机前务必备份数据------别问我是怎么知道的。