超越循环前缀限制的 OFDM-ISAC：迭代 SIC-DFT 原理解析

超越循环前缀限制的 OFDM-ISAC：迭代 SIC-DFT 原理解析

前言

一体化感知与通信（Integrated Sensing and Communication，ISAC）是 5G/6G 时代的重要方向之一。基于 OFDM 的蜂窝波形具有大带宽、高频谱利用率等优势，因此被广泛视为实现 ISAC 的候选体制。然而，传统 OFDM 雷达建模大多假设目标往返时延完全落在循环前缀（CP）长度之内，从而可以忽略符号间干扰（ISI）与载波间干扰（ICI）。在大距离、高载频（如 28 GHz 毫米波）场景下，这一假设经常不再成立。

一、系统模型与基本参数

1.1 OFDM 信号与带宽

考虑一个典型的 OFDM-ISAC 系统，采用 N N N 个子载波、 M M M 个连续 OFDM 符号，子载波间隔为 Δ f \Delta f Δf，信号总带宽为 B B B。则有

B = N Δ f B = N \Delta f B=NΔf

式中：

• B B B 为 OFDM 信号总带宽，单位为 Hz \text{Hz} Hz；

• N N N 为子载波数；

• Δ f \Delta f Δf 为子载波间隔，单位为 Hz \text{Hz} Hz。

有效符号时长（不含 CP）为

T = 1 Δ f T = \frac{1}{\Delta f} T=Δf1

式中：

• T T T 为每个 OFDM 符号的有效时长，单位为 s \text{s} s；

• Δ f \Delta f Δf 含义同上。

在每个符号上添加长度为 T cp T_{\text{cp}} Tcp 的循环前缀（CP），则符号总时长为

T s = T + T cp T_s = T + T_{\text{cp}} Ts=T+Tcp

式中：

• T s T_s Ts 为包含 CP 的 OFDM 符号总时长，单位为 s \text{s} s；

• T T T 为有效符号时长；

• T cp T_{\text{cp}} Tcp 为 CP 时长，单位为 s \text{s} s。

1.2 雷达基本性能指标与 CP 限制

假设信号在自由空间传播，光速为 c 0 c_0 c0，则基于带宽 B B B 的距离分辨率为

Δ R = c 0 2 B \Delta R = \frac{c_0}{2B} ΔR=2Bc0

式中：

• Δ R \Delta R ΔR 为距离分辨率，单位为 m \text{m} m；

• c 0 c_0 c0 为光速，约 3 × 1 0 8 m/s 3\times 10^8\ \text{m/s} 3×108 m/s；

• B B B 为信号带宽。

若对第一个维度（子载波方向）做 N N N 点 FFT，则 RDM 的距离轴上最大可显示距离近似为

R max ⁡ RDM ≈ ( N − 1 ) Δ R R_{\max}^{\text{RDM}} \approx (N-1)\Delta R RmaxRDM≈(N−1)ΔR

式中：

• R max ⁡ RDM R_{\max}^{\text{RDM}} RmaxRDM 为 RDM 上最大距离刻度，单位为 m \text{m} m；

• N N N 为子载波数；

• Δ R \Delta R ΔR 为距离分辨率。

若希望目标回波在时域卷积后仍保持循环卷积结构（从而保持子载波正交性），则目标最大往返时延应不超过 CP 长度，即

2 R c 0 ≤ T cp \frac{2R}{c_0} \le T_{\text{cp}} c02R≤Tcp

式中：

• R R R 为目标距离，单位为 m \text{m} m；

• c 0 c_0 c0 为光速；

• T cp T_{\text{cp}} Tcp 为 CP 时长。

由此可得在 CP 限制下无 ISI 的最大距离为

R max ⁡ CP = c 0 T cp 2 R_{\max}^{\text{CP}} = \frac{c_0 T_{\text{cp}}}{2} RmaxCP=2c0Tcp

式中：

• R max ⁡ CP R_{\max}^{\text{CP}} RmaxCP 为 CP 条件下无 ISI 的最大感知距离，单位为 m \text{m} m；

• c 0 c_0 c0 为光速；

• T cp T_{\text{cp}} Tcp 为 CP 时长。

可以看到，当 R R R 远大于 R max ⁡ CP R_{\max}^{\text{CP}} RmaxCP 时，即使 RDM 频域轴仍能表示该距离（由 Δ R \Delta R ΔR 和 N N N 决定），时域上 CP 已不足以覆盖多径延迟，将不可避免地产生 ISI 与 ICI。

1.3 多普勒分辨率与无模糊速度

以 OFDM 符号重复周期 T s T_s Ts 作为脉冲重复周期（PRF），则

PRF = 1 T s \text{PRF} = \frac{1}{T_s} PRF=Ts1

式中：

• PRF \text{PRF} PRF 为脉冲重复频率，单位为 Hz \text{Hz} Hz；

• T s T_s Ts 为 OFDM 符号总时长。

在观测 M M M 个连续 OFDM 符号的条件下，多普勒频率分辨率为

Δ f d = 1 M T s \Delta f_d = \frac{1}{M T_s} Δfd=MTs1

式中：

• Δ f d \Delta f_d Δfd 为多普勒频率分辨率，单位为 Hz \text{Hz} Hz；

• M M M 为连续 OFDM 符号数；

• T s T_s Ts 为符号周期。

若载波频率为 f c f_c fc，目标径向速度 v v v 与多普勒频移 f d f_d fd 的关系为

f d = 2 v f c c 0 f_d = \frac{2 v f_c}{c_0} fd=c02vfc

式中：

• f d f_d fd 为多普勒频移，单位为 Hz \text{Hz} Hz；

• v v v 为目标径向速度，单位为 m/s \text{m/s} m/s；

• f c f_c fc 为载波频率，单位为 Hz \text{Hz} Hz；

• c 0 c_0 c0 为光速。

由上两式可得速度分辨率

Δ v = c 0 2 f c Δ f d = c 0 2 f c M T s \Delta v = \frac{c_0}{2 f_c} \Delta f_d = \frac{c_0}{2 f_c M T_s} Δv=2fcc0Δfd=2fcMTsc0

式中：

• Δ v \Delta v Δv 为速度分辨率，单位为 m/s \text{m/s} m/s；

• c 0 c_0 c0 为光速；

• f c f_c fc 为载波频率；

• M M M 为 OFDM 符号数；

• T s T_s Ts 为符号周期。

在均匀采样的多普勒频率轴上，无模糊多普勒频率范围为 ± 1 2 T s \pm \tfrac{1}{2T_s} ±2Ts1，对应的速度无模糊范围为

∣ v ∣ max ⁡ = c 0 4 f c T s \lvert v \rvert_{\max} = \frac{c_0}{4 f_c T_s} ∣v∣max=4fcTsc0

式中：

• ∣ v ∣ max ⁡ \lvert v \rvert_{\max} ∣v∣max 为无模糊最大速度的绝对值，单位为 m/s \text{m/s} m/s；

• c 0 c_0 c0、 f c f_c fc、 T s T_s Ts 含义同上。

---

二、目标与回波信号建模

2.1 目标参数

假设场景中有 Q Q Q 个点目标，第 q q q 个目标的距离与速度分别为 R q R_q Rq 和 v q v_q vq，则其往返时延与多普勒频移为

τ q = 2 R q c 0 , f d , q = 2 v q f c c 0 \tau_q = \frac{2 R_q}{c_0}, \qquad f_{d,q} = \frac{2 v_q f_c}{c_0} τq=c02Rq,fd,q=c02vqfc

式中：

• τ q \tau_q τq 为第 q q q 个目标的往返传播时延，单位为 s \text{s} s；

• R q R_q Rq 为第 q q q 个目标的距离，单位为 m \text{m} m；

• f d , q f_{d,q} fd,q 为第 q q q 个目标的多普勒频移，单位为 Hz \text{Hz} Hz；

• v q v_q vq 为第 q q q 个目标的径向速度，单位为 m/s \text{m/s} m/s；

• f c f_c fc 为载波频率，单位为 Hz \text{Hz} Hz；

• c 0 c_0 c0 为光速。

2.2 频域 QAM 符号矩阵

发射端在每个子载波、每个 OFDM 符号时隙上加载 1024-QAM 调制符号，构成频域数据矩阵

S ∈ C N × M \mathbf{S} \in \mathbb{C}^{N \times M} S∈CN×M

式中：

• S \mathbf{S} S 为频域调制符号矩阵；

• C \mathbb{C} C 表示复数域；

• N N N 为子载波数；

• M M M 为 OFDM 符号数。

第 n n n 个子载波、第 m m m 个 OFDM 符号上的调制符号记为 S ( n , m ) S(n,m) S(n,m)。通常对星座进行归一化，使

E [ ∣ S ( n , m ) ∣ 2 ] = 1 \mathbb{E}\big[\lvert S(n,m) \rvert^2\big] = 1 E[∣S(n,m)∣2]=1

式中：

• S ( n , m ) S(n,m) S(n,m) 为第 n n n 个子载波、第 m m m 个符号的复调制符号；

• E [ ⋅ ] \mathbb{E}[\cdot] E[⋅] 为数学期望算子；

• ∣ ⋅ ∣ \lvert \cdot \rvert ∣⋅∣ 为复数的幅度。

2.3 CP 充分时的回波频域模型

在 CP 足够长 （即对所有目标都有 τ q ≤ T cp \tau_q \le T_{\text{cp}} τq≤Tcp）的理想情况下，经过 CP 去除与 FFT 解调后，第 q q q 个目标对频域接收信号的贡献可写为

Y q ( n , m ) = α q b q ( n ) c q ∗ ( m ) S ( n , m ) Y_q(n,m) = \alpha_q b_q(n) c_q^*(m) S(n,m) Yq(n,m)=αqbq(n)cq∗(m)S(n,m)

式中：

• Y q ( n , m ) Y_q(n,m) Yq(n,m) 为第 q q q 个目标在第 n n n 个子载波、第 m m m 个符号位置的频域回波；

• α q \alpha_q αq 为第 q q q 个目标的复反射系数（包含路径损耗与散射特性）；

• b q ( n ) b_q(n) bq(n) 为与时延 τ q \tau_q τq 相关的频域"距离导向向量"；

• c q ( m ) c_q(m) cq(m) 为与多普勒频移 f d , q f_{d,q} fd,q 相关的"速度导向向量"；

• c q ∗ ( m ) c_q^*(m) cq∗(m) 为 c q ( m ) c_q(m) cq(m) 的复共轭；

• S ( n , m ) S(n,m) S(n,m) 为发射的 QAM 符号。

其中，距离导向向量 b q ( n ) b_q(n) bq(n) 和速度导向向量 c q ( m ) c_q(m) cq(m) 为

b q ( n ) = e − j 2 π n Δ f , τ q , n = 0 , ... , N − 1 b_q(n) = e^{-j 2\pi n \Delta f, \tau_q},\quad n = 0,\dots,N-1 bq(n)=e−j2πnΔf,τq,n=0,...,N−1

c q ( m ) = e − j 2 π f d , q m T s , m = 0 , ... , M − 1 c_q(m) = e^{-j 2\pi f_{d,q} m T_s},\quad m = 0,\dots,M-1 cq(m)=e−j2πfd,qmTs,m=0,...,M−1

式中：

• b q ( n ) b_q(n) bq(n) 为第 q q q 个目标在第 n n n 个子载波上的相位旋转因子；

• n n n 为子载波索引；

• Δ f \Delta f Δf 为子载波间隔；

• τ q \tau_q τq 为目标往返时延；

• c q ( m ) c_q(m) cq(m) 为第 q q q 个目标在第 m m m 个 OFDM 符号上的多普勒相位因子；

• m m m 为符号索引；

• f d , q f_{d,q} fd,q 为多普勒频移；

• T s T_s Ts 为符号周期；

• j j j 为虚数单位。

所有目标叠加后，理想"无 ISI/ICI"频域回波矩阵为

Y free ( n , m ) = ∑ q = 1 Q α q b q ( n ) c q ∗ ( m ) S ( n , m ) Y_{\text{free}}(n,m) = \sum_{q=1}^{Q} \alpha_q b_q(n) c_q^*(m) S(n,m) Yfree(n,m)=q=1∑Qαqbq(n)cq∗(m)S(n,m)

式中：

• Y free ( n , m ) Y_{\text{free}}(n,m) Yfree(n,m) 为在 CP 充分条件下、第 n n n 个子载波、第 m m m 个符号位置的总回波；

• Q Q Q 为目标个数；

• 其余变量含义同上。

三、超越 CP 限制的频域干扰模型

当存在远距离目标，使得

τ q > T cp \tau_q > T_{\text{cp}} τq>Tcp

时，CP 不足以覆盖其往返时延。此时，时域卷积不再是纯循环卷积，在频域中表现为符号间干扰（ISI）和载波间干扰（ICI）。

3.1 离散延迟与 CP 长度（采样点）

设系统采样率为

F s = B eff F_s = B_{\text{eff}} Fs=Beff

式中：

• F s F_s Fs 为采样率，单位为 Hz \text{Hz} Hz；

• B eff B_{\text{eff}} Beff 为有效信号带宽，在该模型中通常取 B eff = B B_{\text{eff}} = B Beff=B。

则 CP 长度对应的采样点数为

N cp = ⌊ T cp F s ⌉ N_{\text{cp}} = \Big\lfloor T_{\text{cp}} F_s \Big\rceil Ncp=⌊TcpFs⌉

式中：

• N cp N_{\text{cp}} Ncp 为 CP 长度对应的采样点数；

• T cp T_{\text{cp}} Tcp 为 CP 时长；

• F s F_s Fs 为采样率；

• ⌊ ⋅ ⌉ \lfloor \cdot \rceil ⌊⋅⌉ 表示取最近整数。

第 q q q 个目标的离散延迟 tap 近似为

ℓ q = ⌊ τ q F s ⌉ \ell_q = \Big\lfloor \tau_q F_s \Big\rceil ℓq=⌊τqFs⌉

式中：

• ℓ q \ell_q ℓq 为第 q q q 个目标的离散延迟样本数；

• τ q \tau_q τq 为往返时延；

• F s F_s Fs 为采样率。

若 ℓ q > N cp \ell_q > N_{\text{cp}} ℓq>Ncp，则 CP 无法完全覆盖该目标的时延，将导致 ISI/ICI。

3.2 超出 CP 的"多余时延"

对于 ℓ q > N cp \ell_q > N_{\text{cp}} ℓq>Ncp 的目标，其超出 CP 的多余时延为

τ q ex = τ q − T cp \tau_q^{\text{ex}} = \tau_q - T_{\text{cp}} τqex=τq−Tcp

式中：

• τ q ex \tau_q^{\text{ex}} τqex 为第 q q q 个目标超出 CP 的时延部分，单位为 s \text{s} s；

• τ q \tau_q τq 为总往返时延；

• T cp T_{\text{cp}} Tcp 为 CP 时长。

对应的"多余时延"距离导向向量为

b q ex ( n ) = e − j 2 π n Δ f τ q ex b_q^{\text{ex}}(n) = e^{-j 2\pi n \Delta f \tau_q^{\text{ex}}} bqex(n)=e−j2πnΔfτqex

式中：

• b q ex ( n ) b_q^{\text{ex}}(n) bqex(n) 为与多余时延相关的相位因子；

• n n n 为子载波索引；

• Δ f \Delta f Δf 为子载波间隔；

• τ q ex \tau_q^{\text{ex}} τqex 为多余时延。

3.3 符号间移位矩阵

令符号维度上的移位矩阵为

J 1 ∈ C M × M \mathbf{J}_1 \in \mathbb{C}^{M \times M} J1∈CM×M

其仅在上偏一条对角线 上为 1 1 1，其余元素为 0 0 0，用于表示"向后平移一符号"的操作，即

J 1 ( m , m + 1 ) = 1 , m = 0 , ... , M − 2 \mathbf{J}_1(m,m+1) = 1,\quad m = 0,\dots,M-2 J1(m,m+1)=1,m=0,...,M−2

式中：

• J 1 ( m , m + 1 ) \mathbf{J}_1(m,m+1) J1(m,m+1) 为矩阵 J 1 \mathbf{J}_1 J1 的第 m m m 行、第 m + 1 m+1 m+1 列元素；

• m m m 为符号索引；

• M M M 为符号总数。

对某矩阵右乘 J 1 \mathbf{J}_1 J1 相当于其列索引整体向右平移一位，从而把"上一符号"的数据对齐到当前符号位置，实现 ISI 的建模。

3.4 总体频域模型：含 ISI/ICI

在考虑 CP 不足导致的 ISI 与 ICI 时，接收端的频域信号可建模为

Y = Y free + Y ISI − Y ICI + Z \mathbf{Y} = \mathbf{Y}{\text{free}} + \mathbf{Y}{\text{ISI}} - \mathbf{Y}_{\text{ICI}} + \mathbf{Z} Y=Yfree+YISI−YICI+Z

式中：

• Y ∈ C N × M \mathbf{Y} \in \mathbb{C}^{N\times M} Y∈CN×M 为实际接收的频域信号矩阵；

• Y free \mathbf{Y}_{\text{free}} Yfree 为无 ISI/ICI 时的理想回波矩阵；

• Y ISI \mathbf{Y}_{\text{ISI}} YISI 为符号间干扰（ISI）分量矩阵；

• Y ICI \mathbf{Y}_{\text{ICI}} YICI 为子载波间干扰（ICI）分量矩阵；

• Z \mathbf{Z} Z 为加性复高斯白噪声矩阵。

1）ISI 分量

第 q q q 个目标的 ISI 基础分量可写为

A ISI ( q ) ( n , m ) = b q ex ( n ) c q ∗ ( m ) S ( n , m ) A^{(q)}_{\text{ISI}}(n,m) = b_q^{\text{ex}}(n) c_q^*(m) S(n,m) AISI(q)(n,m)=bqex(n)cq∗(m)S(n,m)

式中：

• A ISI ( q ) ( n , m ) A^{(q)}_{\text{ISI}}(n,m) AISI(q)(n,m) 为在第 n n n 个子载波、第 m m m 个符号上的 ISI 基础项；

• b q ex ( n ) b_q^{\text{ex}}(n) bqex(n) 为多余时延导向向量；

• c q ∗ ( m ) c_q^*(m) cq∗(m) 为多普勒导向向量的共轭；

• S ( n , m ) S(n,m) S(n,m) 为频域调制符号。

将 A ISI ( q ) A^{(q)}{\text{ISI}} AISI(q) 组成矩阵 A ISI ( q ) \mathbf{A}^{(q)}{\text{ISI}} AISI(q)，其右乘移位矩阵 J 1 \mathbf{J}_1 J1，得到

A ISI,shift ( q ) = A ISI ( q ) J 1 \mathbf{A}^{(q)}{\text{ISI,shift}} = \mathbf{A}^{(q)}{\text{ISI}} \mathbf{J}_1 AISI,shift(q)=AISI(q)J1

式中：

• A ISI ( q ) \mathbf{A}^{(q)}{\text{ISI}} AISI(q) 为由 A ISI ( q ) ( n , m ) A^{(q)}{\text{ISI}}(n,m) AISI(q)(n,m) 组成的矩阵；

• A ISI,shift ( q ) \mathbf{A}^{(q)}_{\text{ISI,shift}} AISI,shift(q) 为将上一符号内容对齐到当前符号后的矩阵；

• J 1 \mathbf{J}_1 J1 为移位矩阵。

接下来通过一个与延迟超出 CP 相关的矩阵 Φ q \boldsymbol{\Phi}_q Φq 将 ISI 引入子载波间耦合，最终，第 q q q 个目标的 ISI 分量为

Y ISI ( q ) = α q Φ q A ISI,shift ( q ) \mathbf{Y}^{(q)}_{\text{ISI}} = \alpha_q \boldsymbol{\Phi}q \mathbf{A}^{(q)}{\text{ISI,shift}} YISI(q)=αqΦqAISI,shift(q)

式中：

• Y ISI ( q ) \mathbf{Y}^{(q)}_{\text{ISI}} YISI(q) 为第 q q q 个目标的 ISI 频域分量；

• α q \alpha_q αq 为第 q q q 个目标的复反射系数；

• Φ q ∈ C N × N \boldsymbol{\Phi}_q \in \mathbb{C}^{N\times N} Φq∈CN×N 为第 q q q 个目标对应的干扰耦合矩阵；

• A ISI,shift ( q ) \mathbf{A}^{(q)}_{\text{ISI,shift}} AISI,shift(q) 为移位后的 ISI 基础矩阵。

多目标的 ISI 总分量为

Y ISI = ∑ q = 1 Q Y ISI ( q ) \mathbf{Y}{\text{ISI}} = \sum{q=1}^{Q} \mathbf{Y}^{(q)}_{\text{ISI}} YISI=q=1∑QYISI(q)

式中：

• Y ISI \mathbf{Y}_{\text{ISI}} YISI 为所有目标引起的总 ISI；

• Y ISI ( q ) \mathbf{Y}^{(q)}_{\text{ISI}} YISI(q) 为第 q q q 个目标的 ISI 分量；

• Q Q Q 为目标数。

2）ICI 分量

第 q q q 个目标在"本符号内"的 ICI 基础分量为

A ICI ( q ) ( n , m ) = b q ( n ) c q ∗ ( m ) S ( n , m ) A^{(q)}_{\text{ICI}}(n,m) = b_q(n) c_q^*(m) S(n,m) AICI(q)(n,m)=bq(n)cq∗(m)S(n,m)

式中：

• A ICI ( q ) ( n , m ) A^{(q)}_{\text{ICI}}(n,m) AICI(q)(n,m) 为 ICI 基础项；

• b q ( n ) b_q(n) bq(n) 为距离导向向量；

• c q ∗ ( m ) c_q^*(m) cq∗(m) 为多普勒导向向量的共轭；

• S ( n , m ) S(n,m) S(n,m) 为调制符号。

组成矩阵 A ICI ( q ) \mathbf{A}^{(q)}_{\text{ICI}} AICI(q) 后，经 Φ q \boldsymbol{\Phi}_q Φq 作用，第 q q q 个目标的 ICI 分量为

Y ICI ( q ) = α q Φ q A ICI ( q ) \mathbf{Y}^{(q)}_{\text{ICI}} = \alpha_q \boldsymbol{\Phi}q \mathbf{A}^{(q)}{\text{ICI}} YICI(q)=αqΦqAICI(q)

式中：

• Y ICI ( q ) \mathbf{Y}^{(q)}_{\text{ICI}} YICI(q) 为第 q q q 个目标的 ICI 分量；

• α q \alpha_q αq、 Φ q \boldsymbol{\Phi}_q Φq 含义同上；

• A ICI ( q ) \mathbf{A}^{(q)}{\text{ICI}} AICI(q) 为由 A ICI ( q ) ( n , m ) A^{(q)}{\text{ICI}}(n,m) AICI(q)(n,m) 组成的矩阵。

ICI 总分量为

Y ICI = ∑ q = 1 Q Y ICI ( q ) \mathbf{Y}{\text{ICI}} = \sum{q=1}^{Q} \mathbf{Y}^{(q)}_{\text{ICI}} YICI=q=1∑QYICI(q)

式中：

• Y ICI \mathbf{Y}_{\text{ICI}} YICI 为所有目标引起的总 ICI；

• Y ICI ( q ) \mathbf{Y}^{(q)}_{\text{ICI}} YICI(q) 为第 q q q 个目标的 ICI 分量；

• Q Q Q 为目标数。

至此， Y \mathbf{Y} Y 的完整频域接收模型如前所示。

---

四、干扰矩阵 Φ q \boldsymbol{\Phi}_q Φq 的构造与性质

当 ℓ q ≤ N cp \ell_q \le N_{\text{cp}} ℓq≤Ncp 时，第 q q q 个目标完全落在 CP 内，不产生额外 ISI/ICI，此时

Φ q = 0 N × N \boldsymbol{\Phi}q = \mathbf{0}{N\times N} Φq=0N×N

式中：

• Φ q \boldsymbol{\Phi}_q Φq 为第 q q q 个目标的干扰矩阵；

• 0 N × N \mathbf{0}_{N\times N} 0N×N 为 N × N N\times N N×N 零矩阵；

• ℓ q \ell_q ℓq 为离散延迟；

• N cp N_{\text{cp}} Ncp 为 CP 样本数。

当 ℓ q > N cp \ell_q > N_{\text{cp}} ℓq>Ncp 时，定义

K q = ℓ q − N cp K_q = \ell_q - N_{\text{cp}} Kq=ℓq−Ncp

式中：

• K q K_q Kq 为超出 CP 的离散采样点数；

• ℓ q \ell_q ℓq 为总离散延迟；

• N cp N_{\text{cp}} Ncp 为 CP 样本数。

此时 Φ q \boldsymbol{\Phi}_q Φq 的元素 ϕ q ( n , n ′ ) \phi_q(n,n') ϕq(n,n′) 可写为

ϕ q ( n , n ′ ) = 1 N ∑ i = 0 K q − 1 e j 2 π ( n ′ − n ) i N \phi_q(n,n') = \frac{1}{N} \sum_{i=0}^{K_q-1} e^{j 2\pi (n' - n) \frac{i}{N}} ϕq(n,n′)=N1i=0∑Kq−1ej2π(n′−n)Ni

式中：

• ϕ q ( n , n ′ ) \phi_q(n,n') ϕq(n,n′) 为矩阵 Φ q \boldsymbol{\Phi}_q Φq 的第 n n n 行、第 n ′ n' n′ 列元素；

• n n n 为接收子载波索引；

• n ′ n' n′ 为发送子载波索引；

• K q K_q Kq 为超出 CP 的采样点数；

• N N N 为子载波个数；

• i i i 为时间采样索引。

令

Δ n = n ′ − n \Delta n = n' - n Δn=n′−n

式中：

• Δ n \Delta n Δn 为子载波索引差，即频域"间隔"；

• n , n ′ n,n' n,n′ 含义同上。

当 Δ n = 0 \Delta n = 0 Δn=0 时，上式退化为

ϕ q ( n , n ) = K q N \phi_q(n,n) = \frac{K_q}{N} ϕq(n,n)=NKq

式中：

• ϕ q ( n , n ) \phi_q(n,n) ϕq(n,n) 为干扰矩阵的对角元素；

• K q K_q Kq 为超出 CP 的采样点数；

• N N N 为子载波数。

当 Δ n ≠ 0 \Delta n \ne 0 Δn=0 时，上式为几何级数，可写为

ϕ q ( n , n ′ ) = 1 N 1 − r K q 1 − r \phi_q(n,n') = \frac{1}{N} \frac{1 - r^{K_q}}{1 - r} ϕq(n,n′)=N11−r1−rKq

其中

r = e j 2 π Δ n N r = e^{j 2\pi \frac{\Delta n}{N}} r=ej2πNΔn

式中：

• r r r 为几何级数公比；

• Δ n \Delta n Δn 为子载波索引差；

• K q K_q Kq 为求和项数；

• N N N 为子载波数。

由此可见， Φ q \boldsymbol{\Phi}_q Φq 描述了超出 CP 的那段时域片段在频域中如何造成子载波间耦合，进而产生 ISI/ICI。

五、距离--多普勒图（RDM）的构造

5.1 频域匹配滤波

在频域中，利用已知发射符号矩阵 S \mathbf{S} S，可对接收矩阵 Y \mathbf{Y} Y 进行匹配滤波：

Y ~ ( n , m ) = Y ( n , m ) S ∗ ( n , m ) \widetilde{Y}(n,m) = Y(n,m) S^*(n,m) Y (n,m)=Y(n,m)S∗(n,m)

式中：

• Y ~ ( n , m ) \widetilde{Y}(n,m) Y (n,m) 为匹配滤波后的频域信号；

• Y ( n , m ) Y(n,m) Y(n,m) 为接收频域信号；

• S ∗ ( n , m ) S^*(n,m) S∗(n,m) 为发射符号的复共轭。

矩阵形式为

Y ~ = Y ⊙ S ∗ \widetilde{\mathbf{Y}} = \mathbf{Y} \odot \mathbf{S}^* Y =Y⊙S∗

式中：

• Y ~ \widetilde{\mathbf{Y}} Y 为匹配滤波后的频域矩阵；

• ⊙ \odot ⊙ 为 Hadamard 乘积（元素逐点相乘）；

• S ∗ \mathbf{S}^* S∗ 为矩阵 S \mathbf{S} S 的逐元素共轭；

• Y \mathbf{Y} Y 为接收矩阵。

5.2 距离向 IFFT

对每个符号 m m m，在子载波维度上进行 N N N 点逆 FFT，实现从频域到距离域的变换。一般形式为

χ ( r , m ) = ∑ n = 0 N − 1 Y ~ ( n , m ) e j 2 π n r N \chi(r,m) = \sum_{n=0}^{N-1} \widetilde{Y}(n,m) e^{j 2\pi \frac{n r}{N}} χ(r,m)=n=0∑N−1Y (n,m)ej2πNnr

式中：

• χ ( r , m ) \chi(r,m) χ(r,m) 为第 r r r 个"距离单元"、第 m m m 个符号的匹配输出；

• r r r 为距离单元索引， r = 0 , ... , N − 1 r=0,\dots,N-1 r=0,...,N−1；

• n n n 为子载波索引；

• Y ~ ( n , m ) \widetilde{Y}(n,m) Y (n,m) 为匹配滤波结果。

距离轴的物理刻度为

R r = r Δ R R_r = r \Delta R Rr=rΔR

式中：

• R r R_r Rr 为第 r r r 个距离单元对应的实际距离，单位为 m \text{m} m；

• r r r 为距离单元索引；

• Δ R \Delta R ΔR 为距离分辨率。

5.3 多普勒向 FFT

在多普勒维度，对每个距离单元 r r r 的 M M M 个符号做 M M M 点 FFT，得到

χ ( r , k ) = ∑ m = 0 M − 1 χ ( r , m ) e − j 2 π m k M \chi(r,k) = \sum_{m=0}^{M-1} \chi(r,m) e^{-j 2\pi \frac{m k}{M}} χ(r,k)=m=0∑M−1χ(r,m)e−j2πMmk

式中：

• χ ( r , k ) \chi(r,k) χ(r,k) 为第 r r r 个距离单元、第 k k k 个多普勒单元的匹配输出；

• k k k 为多普勒频率索引，一般通过 FFT 加频移实现居中；

• m m m 为符号索引；

• χ ( r , m ) \chi(r,m) χ(r,m) 为距离向 IFFT 后结果。

多普勒频率与速度的对应关系为

f d , k = k M T s , v k = c 0 f d , k 2 f c f_{d,k} = \frac{k}{M T_s},\quad v_k = \frac{c_0 f_{d,k}}{2 f_c} fd,k=MTsk,vk=2fcc0fd,k

式中：

• f d , k f_{d,k} fd,k 为第 k k k 个多普勒单元对应的频率，单位为 Hz \text{Hz} Hz；

• v k v_k vk 为第 k k k 个多普勒单元对应的径向速度，单位为 m/s \text{m/s} m/s；

• k k k 为多普勒索引；

• M M M 为符号数；

• T s T_s Ts 为符号周期；

• c 0 c_0 c0 为光速；

• f c f_c fc 为载波频率。

5.4 RDM 幅度谱与归一化

得到 χ ( r , k ) \chi(r,k) χ(r,k) 后，可构造 RDM 的幅度谱

RDM ( r , k ) = 20 log ⁡ 10 ( ∣ χ ( r , k ) ∣ max ⁡ r ′ , k ′ ∣ χ ( r ′ , k ′ ) ∣ + ε ) \text{RDM}(r,k) = 20 \log_{10} \left( \frac{\lvert \chi(r,k) \rvert} {\max_{r',k'} \lvert \chi(r',k') \rvert + \varepsilon} \right) RDM(r,k)=20log10(maxr′,k′∣χ(r′,k′)∣+ε∣χ(r,k)∣)

式中：

• RDM ( r , k ) \text{RDM}(r,k) RDM(r,k) 为第 r r r 个距离单元、第 k k k 个多普勒单元的功率谱（单位为 dB \text{dB} dB）；

• ∣ χ ( r , k ) ∣ \lvert \chi(r,k) \rvert ∣χ(r,k)∣ 为复数 χ ( r , k ) \chi(r,k) χ(r,k) 的幅度；

• max ⁡ r ′ , k ′ ∣ χ ( r ′ , k ′ ) ∣ \max_{r',k'} \lvert \chi(r',k') \rvert maxr′,k′∣χ(r′,k′)∣ 为所有距离--多普勒点上的最大幅度，用于归一化；

• ε \varepsilon ε 为极小正数，防止对 0 0 0 取对数；

• r , k r,k r,k 为距离和多普勒索引。

---

六、迭代式 SIC-DFT 算法

在仿真环境中， Y free \mathbf{Y}{\text{free}} Yfree、 Y ISI \mathbf{Y}{\text{ISI}} YISI、 Y ICI \mathbf{Y}_{\text{ICI}} YICI 均被显式构造，因此可以视为已知，用于研究理想"Oracle 级"迭代干扰抵消的性能上界。

6.1 频域干扰分量定义

由总体模型可定义总干扰分量为

Y intf = Y ISI − Y ICI \mathbf{Y}{\text{intf}} = \mathbf{Y}{\text{ISI}} - \mathbf{Y}_{\text{ICI}} Yintf=YISI−YICI

式中：

• Y intf \mathbf{Y}_{\text{intf}} Yintf 为总干扰（ISI 与 ICI 组合）频域矩阵；

• Y ISI \mathbf{Y}_{\text{ISI}} YISI 为 ISI 分量矩阵；

• Y ICI \mathbf{Y}_{\text{ICI}} YICI 为 ICI 分量矩阵。

6.2 迭代 SIC 更新过程

令迭代次数上限为 L L L，初始化第 0 0 0 次迭代的信号为

Y ( 0 ) = Y \mathbf{Y}^{(0)} = \mathbf{Y} Y(0)=Y

式中：

• Y ( 0 ) \mathbf{Y}^{(0)} Y(0) 为第 0 0 0 次迭代时的频域接收矩阵；

• Y \mathbf{Y} Y 为原始接收矩阵。

在第 i i i 次迭代中（ i = 1 , ... , L i=1,\dots,L i=1,...,L），做如下更新：

Y ( i ) = Y ( i − 1 ) − 1 L Y intf \mathbf{Y}^{(i)} = \mathbf{Y}^{(i-1)} - \frac{1}{L} \mathbf{Y}_{\text{intf}} Y(i)=Y(i−1)−L1Yintf

式中：

• Y ( i ) \mathbf{Y}^{(i)} Y(i) 为第 i i i 次迭代后的频域信号；

• Y ( i − 1 ) \mathbf{Y}^{(i-1)} Y(i−1) 为第 i − 1 i-1 i−1 次迭代的频域信号；

• Y intf \mathbf{Y}_{\text{intf}} Yintf 为总干扰矩阵；

• L L L 为总迭代次数。

形式上，在完成 L L L 次迭代后，有

Y ( L ) = Y − Y intf = Y free + Z \mathbf{Y}^{(L)} = \mathbf{Y} - \mathbf{Y}{\text{intf}} = \mathbf{Y}{\text{free}} + \mathbf{Z} Y(L)=Y−Yintf=Yfree+Z

式中：

• Y ( L ) \mathbf{Y}^{(L)} Y(L) 为第 L L L 次迭代后的频域信号；

• Y \mathbf{Y} Y 为真实接收信号；

• Y intf \mathbf{Y}_{\text{intf}} Yintf 为总干扰；

• Y free \mathbf{Y}_{\text{free}} Yfree 为无 ISI/ICI 的理想回波；

• Z \mathbf{Z} Z 为噪声矩阵。

在实际系统中， Y ISI \mathbf{Y}{\text{ISI}} YISI、 Y ICI \mathbf{Y}{\text{ICI}} YICI 通常未知，需要通过估计目标参数并重构干扰项来实现真正的 SIC；此处的迭代模型主要用于分析"若干扰能被完美估计"时，超越 CP 限制仍能恢复高质量 RDM 的潜力。

6.3 与简单 DFT 基线的对比

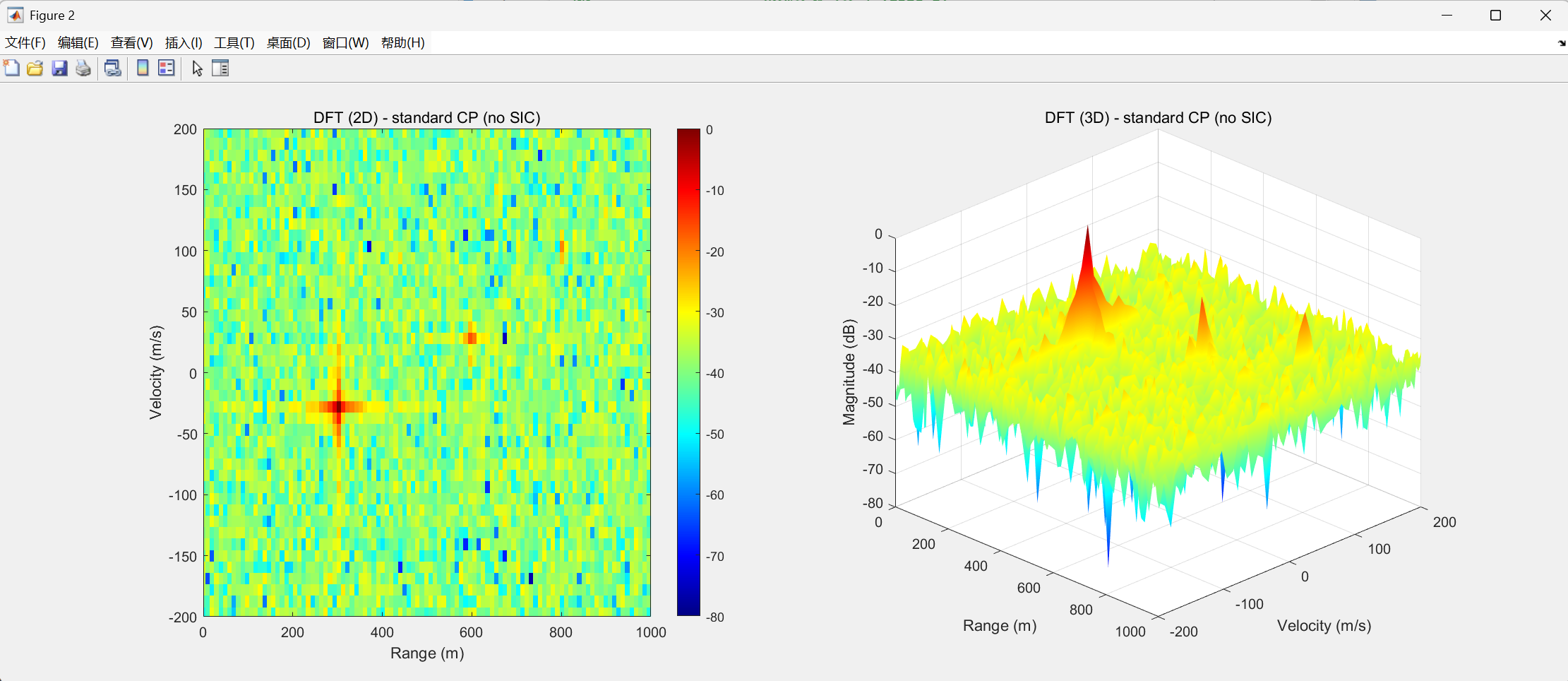
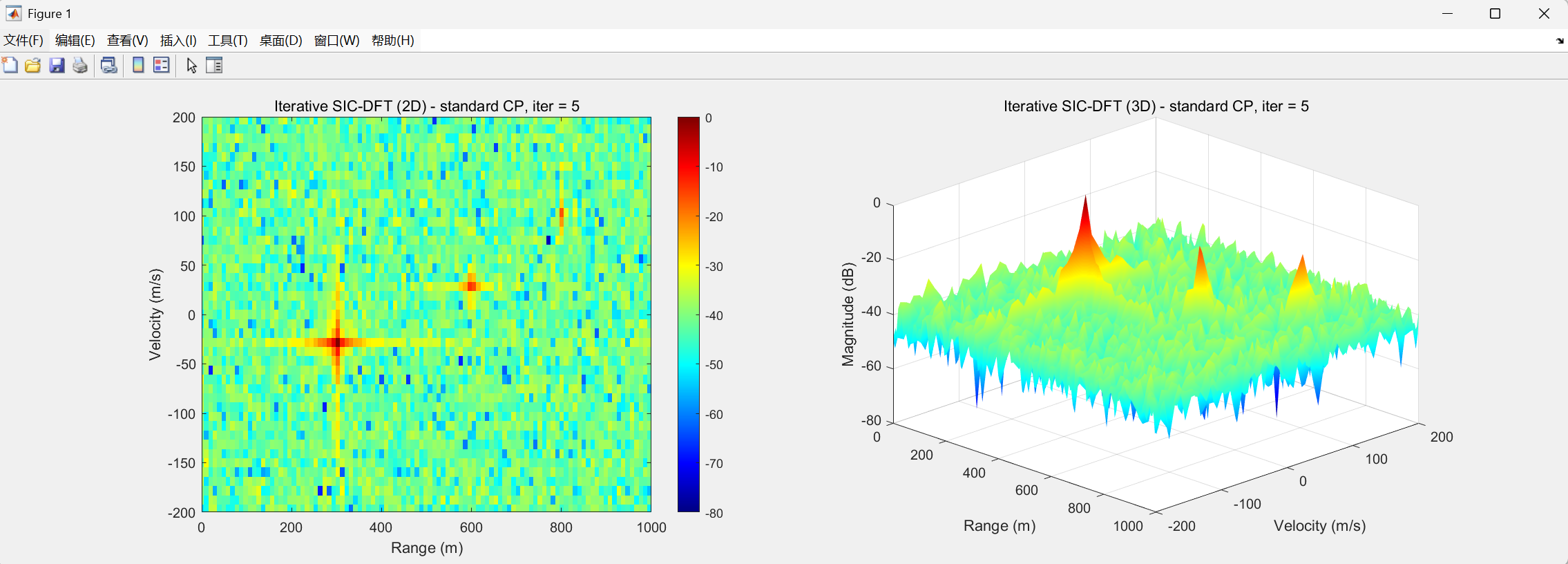
• 基线方案（无 SIC） ：直接利用 Y \mathbf{Y} Y 构造 RDM，即在构造匹配滤波与二维 FFT 时，包含所有 ISI/ICI。此时 RDM 中的目标峰将受到明显的旁瓣上升与伪峰污染。

• 迭代 SIC-DFT 方案 ：对每次迭代后的 Y ( i ) \mathbf{Y}^{(i)} Y(i) 构造 RDM，可以观察到随着 i i i 增大，RDM 中主峰逐渐变得尖锐、旁瓣降低，远距离目标在短 CP 条件下仍然可以被清晰分辨。

总结

本文围绕"OFDM-ISAC 超越 CP 限制"这一主题，从公式与原理角度对仿真模型所隐含的数学机制进行了系统梳理，主要包括：

1. 从 OFDM 基本参数出发，推导了距离分辨率、速度分辨率、CP 限制下的最大无 ISI 距离等关键指标，明确了RDM 轴范围 与CP 物理约束之间的差异。

2. 在 CP 足够的前提下，给出了多目标场景下的频域回波模型，并用导向向量 b q ( n ) b_q(n) bq(n)、 c q ( m ) c_q(m) cq(m) 统一描述时延与多普勒效应。

3. 在 CP 不足时，构建了包含 ISI 与 ICI 的完整频域模型，通过干扰矩阵 Φ q \boldsymbol{\Phi}_q Φq 精确刻画了"超出 CP 的时域片段"在频域中的能量泄漏与子载波耦合。

4. 基于频域匹配滤波和二维 FFT，给出了 RDM 的构造方法及其距离--速度轴的物理映射。

5. 引入迭代 SIC-DFT 算法，对频域干扰进行多轮抵消，理论上可逐步逼近无 ISI/ICI 的理想回波 Y free \mathbf{Y}_{\text{free}} Yfree，显著提升在短 CP 条件下的远距离感知性能。

从工程角度看，当标准通信 CP 显著短于雷达设计所需 CP 时，直接延长 CP 会明显降低频谱效率。本文分析的"超越 CP 限制 + 迭代式频域 SIC"思路，为在复用现有通信波形的前提下扩展雷达感知距离、提升感知性能提供了重要的理论基础与算法范式。