有起点、起绕点、转弯绕点、终点这四个点以及一个时间,每个点都有经纬度、高度,用于生成在给定时间内,飞行这四个点的顺序,由于时间的问题,肯定需要生成一个向终点飞行的结束绕圈的脱离点
效果
直径圆
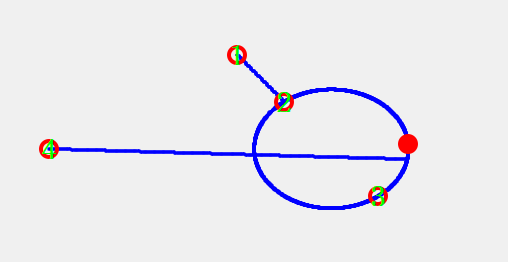
- 起绕点<->转弯绕点为直径
8字圆(双直径)
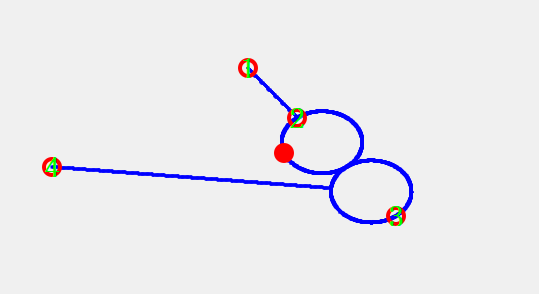
- 圆 A:entry → 中点 前半段为直径
- 圆心 CA = entry→中点 中点
- 半径 R = |entry-turn|/4
- 圆 B:中点 → turn 后半段为直径
- 圆心 CB = 中点→turn 中点
- 半径同 R
- 两圆仅在中点相切,走向相反,组成 ∞ 形
- 顺序:entry → A(π) → B(π) → turn → B(π) → A(π) → entry → ...
跑道型 = 两半圆 + 2 条正方形直边 ,先圆后直
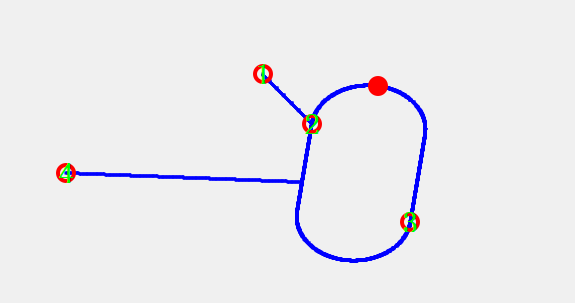
cpp
顺时针 顺序
边1
entry◀─────────▶p1
│ │
│ │ 边2
│ │
▼ ▼
p4◀─────────▶turn
边3
逆时针 顺序
边4
entry◀─────────▶p4
│ ▲
边1│ │ 边3
│ │
▼ │
p1◀─────────▶turn
边2
半圆 A 贴在 边1中点 外侧 → 圆心即中点
半圆 B 贴在 边3中点 外侧 → 圆心即中点
走向:
entry → A(π) → p1 → 边2 → turn → B(π) → p4 → 边4 →entry跑道型 = 两半圆 + 2 条正方形直边 ,先直后圆
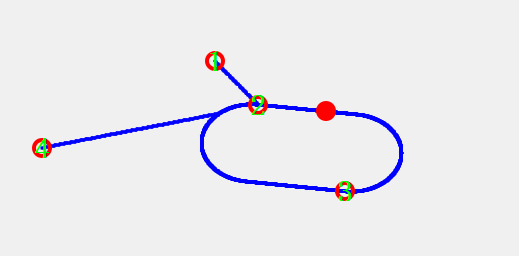
cpp
顺时针顺序:
边1
entry ◀──────▶ p1
│ │
│ │ 边2
│ │
▼ ▼
p4 ◀──────▶ turn
边3
逆时针顺序:
边4
entry ◀──────▶ p4
│ ▲
边1│ │边3
│ │
▼ │
p1 ◀──────▶ turn
边2
半圆A贴在边2中点外侧(圆心为边2中点)
半圆B贴在边4中点外侧(圆心为边4中点)
走向(顺时针):
entry → 边1 → p1 → A(π) → turn → 边3 → p4 → B(π) → entry代码
cpp
#pragma once
#include <QGuiApplication>
#include <QTime>
#include <QTimer>
#include <QtWidgets/QApplication>
#include <QtWidgets/QWidget>
#include <QPainter>
#include <QtMath>
/*
在c++qt中有起点、起绕点、转弯绕点、终点这四个点以及一个时间,每个点都有经纬度,高度,
写一套算法用于生成在给定时间内,飞行这四个点的顺序,由于时间的问题,肯定需要生成一个向终点飞行的结束绕圈的脱离点,
*/
// 基本点
struct WayPoint {
double t; // 秒
double lat, lon; // 弧度
double h; // 米
WayPoint() = default;
WayPoint(double _t, double _lat, double _lon, double _h)
:t(_t), lat(_lat), lon(_lon), h(_h) {
}
// 相等比较
bool operator==(const WayPoint& other) const {
return qFuzzyCompare(t, other.t)
&& qFuzzyCompare(lat, other.lat)
&& qFuzzyCompare(lon, other.lon)
&& qFuzzyCompare(h, other.h);
}
};
// 把 lat/lon(弧度) 转成局部平面米制坐标,以 p0 为原点
static void ll2local(double lat0, double lon0,
double lat, double lon,
double& x, double& y)
{
const double Re = 6371000; // 地球平均半径
double dlat = lat - lat0;
double dlon = lon - lon0;
y = dlat * Re;
x = dlon * Re * cos(lat0);
}
// 平面米制坐标反算回 lat/lon
static void local2ll(double lat0, double lon0,
double x, double y,
double& lat, double& lon)
{
const double Re = 6371000;
double dlat = y / Re;
double dlon = x / (Re * cos(lat0));
lat = lat0 + dlat;
lon = lon0 + dlon;
}
// 转弯模型
enum TurnModel
{
TM_CIRCLE, //直径圆
TM_8_CIRCLE,// 8字圆(双直径)
TM_RUNWAY_CIRCLE_LINE, // 跑道型 = 两半圆 + 2 条正方形直边 ,先圆后直
TM_RUNWAY_LINE_CIRCLE, // 跑道型 = 两半圆 + 2 条正方形直边 ,先直后圆
};
// 旋转方向
enum RotationDirection
{
RD_CLOCKWISE,// 顺时针
RD_COUNTERCLOCKWISE// 逆时针
};
/* 函数:生成航迹,时间驱动,形状固定
* 输入:4 个航点(rad),总时间(s),地速(m/s),采样周期(s)
* 输出:带时间戳的完整航迹
* 极端时间:start→P→final 或 start→final 直线
*/
static QVector<WayPoint> planDiameterCircle2(
const WayPoint& start, /* 起点*/
const WayPoint& entry, /* 起绕点*/
const WayPoint& turn, /* 转弯绕点*/
const WayPoint & final, /* 终点*/
double Ttotal, /* 总飞行时间,单位:秒(s) */
double V, /* 地速,单位:米/秒(m/s) */
double dt, /* 采样周期,单位:秒(s) */
TurnModel model = TM_CIRCLE,
RotationDirection dir = RD_CLOCKWISE
)
{
QVector<WayPoint> path; // 输出航迹
/* 0. 局部坐标:以 start 为原点,米制(x,y) */
double xs, ys, xe, ye, xt, yt, xf, yf;
ll2local(start.lat, start.lon, start.lat, start.lon, xs, ys); // (0,0)
ll2local(start.lat, start.lon, entry.lat, entry.lon, xe, ye); // entry 向量(m)
ll2local(start.lat, start.lon, turn.lat, turn.lon, xt, yt); // turn 向量(m)
ll2local(start.lat, start.lon, final.lat, final.lon, xf, yf); // final 向量(m)
/* 1. 起点→起绕点 直线长度 & 时间 */
double leg1 = hypot(xe - xs, ye - ys); // 长度,单位:米(m)
double t1 = leg1 / V; // 时间,单位:秒(s) t1 = 距离/速度
/* 2. 极端时间:t1 ≥ Ttotal 时,无法到达 entry,只能 start→P→final 两段直线 */
if (t1 >= Ttotal)
{
/* 2.0 更极端:直飞 final 就够,连中间点都不需要 */
double legSF = hypot(xf - xs, yf - ys); // start→final 长度(m)
double tSF = legSF / V; // 所需时间(s)
if (tSF >= Ttotal) { // 连直飞都来不及
int N = qCeil(Ttotal / dt); // 总采样点数
for (int i = 0; i <= N; i++) {
double k = i / double(N); // 归一化时间 0→1
double x = xs + k * (xf - xs); // 直线插值 x(m)
double y = ys + k * (yf - ys); // 直线插值 y(m)
double h = start.h + k * (final.h - start.h); // 高度插值(m)
double lat, lon;
local2ll(start.lat, start.lon, x, y, lat, lon);
path.append(WayPoint(k * Ttotal, lat, lon, h)); // 时间戳(s)
}
return path; // early return
}
/* 2.1 两段直线:start→P→final,总路程 = V·Ttotal
* 设 P = start + s·(entry-start),解二次方程求 s∈[0,1] */
double dx = xe - xs, dy = ye - ys; // start→entry 向量(m)
double fx = xf - xs, fy = yf - ys; // start→final 向量(m)
double a = dx * dx + dy * dy; // |entry-start|² (m²)
double b = dx * fx + dy * fy; // dot(entry-start, final-start) (m²)
double c = fx * fx + fy * fy; // |final-start|² (m²)
double S = V * Ttotal; // 总路程(m) S = V·Ttotal
double delta = b * b - a * (c - S * S); // 二次方程判别式(m⁴)
double s = 0; // 脱离比例 0≤s≤1
if (delta >= 0) {
double s1 = (-b + qSqrt(delta)) / a; // 公式解 1
double s2 = (-b - qSqrt(delta)) / a; // 公式解 2
s = qBound(0.0, s1, 1.0);
if (s < 0 || s > 1) s = qBound(0.0, s2, 1.0);
}
/* 2.2 脱离点 P(局部米) */
double px = xs + s * dx; // P.x = start.x + s·dx(m)
double py = ys + s * dy; // P.y = start.y + s·dy(m)
double ph = start.h + s * (entry.h - start.h); // P.h 线性插值(m)
/* 2.3 统一时间轴采样:总点数 = Ttotal/dt,全程匀速 V */
int N = qCeil(Ttotal / dt);
for (int i = 0; i <= N; i++) {
double k = i / double(N); // 归一化时间 0→1
double x, y, h;
if (k <= s) { // 第一段 start→P
double r = k / s; // 路程比例 0→1
x = xs + r * (px - xs); // 直线插值 x(m)
y = ys + r * (py - ys); // 直线插值 y(m)
h = start.h + r * (ph - start.h);// 直线插值 h(m)
}
else { // 第二段 P→final
double r = (k - s) / (1.0 - s); // 路程比例 0→1
x = px + r * (xf - px); // 直线插值 x(m)
y = py + r * (yf - py); // 直线插值 y(m)
h = ph + r * (final.h - ph); // 直线插值 h(m)
}
double lat, lon;
local2ll(start.lat, start.lon, x, y, lat, lon);
path.append(WayPoint(k * Ttotal, lat, lon, h)); // 时间戳(s)
}
return path; // early return
}
/* 3. 正常情况:时间足够,生成 start→entry 完整直线 */
int N1 = qCeil(t1 / dt);
for (int i = 0; i <= N1; i++) {
double s = i * dt / t1; // 归一化路程 0→1
double x = xs + (xe - xs) * s; // 直线插值 x(m)
double y = ys + (ye - ys) * s; // 直线插值 y(m)
double h = start.h + (entry.h - start.h) * s; // 直线插值 h(m)
double lat, lon;
local2ll(start.lat, start.lon, x, y, lat, lon);
path.append(WayPoint(i * dt, lat, lon, h)); // 时间戳(s)
}
/* 4. 剩余时间 Tleft = Ttotal - t1 */
double Tleft = Ttotal - t1; // 单位:秒(s)
/* 4.0 极端:剩余时间只够 entry→final 直飞,不绕圈 */
double legSF = hypot(xf - xe, yf - ye); // entry→final 长度(m)
double tSF = legSF / V; // 所需时间(s)
if (tSF >= Tleft) { // 连切线都不够
int N = qCeil(Tleft / dt);
for (int i = 0; i <= N; i++) {
double k = i / double(N); // 归一化时间 0→1
double x = xe + k * (xf - xe); // 直线插值 x(m)
double y = ye + k * (yf - ye); // 直线插值 y(m)
double h = entry.h + k * (final.h - entry.h); // 直线插值 h(m)
double lat, lon;
local2ll(start.lat, start.lon, x, y, lat, lon);
path.append(WayPoint(t1 + k * Tleft, lat, lon, h)); // 时间戳(s)
}
return path; // early return
}
const int cw = (dir == RD_CLOCKWISE) ? 1 : -1;
if (model == TM_CIRCLE)
{
/*起绕点<->转弯绕点为直径*/
/* 5. 固定几何:直径圆 + 切线(形状固定,时间可任意) */
double cx = (xe + xt) * 0.5; // 圆心 x(m)
double cy = (ye + yt) * 0.5; // 圆心 y(m)
double R = hypot(xt - xe, yt - ye) * 0.5; // 半径(m) R = |entry-turn|/2
double OFx = xf - cx, OFy = yf - cy; // 圆心→final 向量(m)
double D = hypot(OFx, OFy); // 圆心到 final 距离(m)
double alphaExit = qAcos(R / D); // 切线角(rad) cosα = R/D
double ang0 = qAtan2(ye - cy, xe - cx); // entry 对应角度(rad)
double angEnd = qAtan2(OFy, OFx) - alphaExit; // 切点角度(rad)
if (angEnd < ang0) angEnd += 2 * M_PI; // 保证在 ang0 之后
double Sline = qSqrt(D * D - R * R); // 切线长度(m) Sline = √(D²-R²)
double TlineMin = Sline / V; // 最低切线时间(s)
double TarcMax = Tleft - TlineMin; // 留给圆弧的极限时间(s)
if (TarcMax < 0) TarcMax = 0; // 下限 0
double Tarc = TarcMax; // 真实圆弧时间(s)
double Tline = Tleft - Tarc; // 真实切线时间(s)
double theta = Tarc * V / R; // 真实绕角(rad) θ = Tarc·V/R
double omega = theta / Tarc; // 角速度(rad/s) ω = θ/Tarc
/* 6. 圆弧段:绕 θ 角,脱离点始终在切点 */
int Narc = qCeil(Tarc / dt); // 圆弧采样点数
for (int i = 0; i <= Narc; i++) {
double tau = i * dt; // 当前弧段时间(s)
double a = ang0 - omega * tau* cw; // 当前角度(rad)
double x = cx + R * qCos(a); // 当前 x(m)
double y = cy + R * qSin(a); // 当前 y(m)
double h = entry.h + (turn.h - entry.h) * (tau / Tarc); // 高度线性(m)
double lat, lon;
local2ll(start.lat, start.lon, x, y, lat, lon);
path.append(WayPoint(t1 + tau, lat, lon, h)); // 时间戳(s)
}
/* 7. 直线段:切点 → final */
double px = cx + R * qCos(ang0 - theta * cw); // 切点 x(m)
double py = cy + R * qSin(ang0 - theta * cw); // 切点 y(m)
double ph = entry.h + (turn.h - entry.h); // 切点高度(m)
int Nline = qCeil(Tline / dt); // 切线采样点数
for (int i = 0; i <= Nline; i++) {
double s = i * dt / Tline; // 归一化路程 0→1
double x = px + s * (xf - px); // 直线插值 x(m)
double y = py + s * (yf - py); // 直线插值 y(m)
double h = ph + s * (final.h - ph); // 直线插值 h(m)
double lat, lon;
local2ll(start.lat, start.lon, x, y, lat, lon);
path.append(WayPoint(t1 + Tarc + i * dt, lat, lon, h)); // 时间戳(s)
}
}
else if (model == TM_8_CIRCLE)
{
/* 5. 模式二:8 字双半圆 + 切线脱离
* 圆 A:entry → 中点 前半段为直径
* 圆心 CA = entry→中点 中点
* 半径 R = |entry-turn|/4
* 圆 B:中点 → turn 后半段为直径
* 圆心 CB = 中点→turn 中点
* 半径同 R
* 两圆仅在中点相切,走向相反,组成 ∞ 形
* 顺序:entry → A(π) → B(π) → turn → B(π) → A(π) → entry → ...
* 脱离:当前圆上切点 → final 直线
*/
/* 先算出 entry↔turn 中点(公共相切点)*/
double mx = (xe + xt) * 0.5; // 中点 x(m)
double my = (ye + yt) * 0.5; // 中点 y(m)
double R = hypot(xt - xe, yt - ye) * 0.25; // 公共半径(m) R = |entry-turn|/4
/* 圆 A:entry → 中点 前半段直径 */
double CAx = (xe + mx) * 0.5; // 圆A中心 x(m) CA = entry→中点 中点
double CAy = (ye + my) * 0.5; // 圆A中心 y(m)
/* 圆 B:中点 → turn 后半段直径 */
double CBx = (mx + xt) * 0.5; // 圆B中心 x(m) CB = 中点→turn 中点
double CBy = (my + yt) * 0.5; // 圆B中心 y(m)
/* 5.2 单半圈时间:Tsemi = π·R / V (s) */
double Tsemi = M_PI * R / V; // 半圈时间(s) Tsemi = πR/V
/* 5.5 高度:每半圈增量 */
int nSemiTot = qCeil(Tleft / Tsemi);
double dHsemi = (turn.h - entry.h) / nSemiTot;// 每半圈高度增量
/* 5.6 真 ∞ 8 字 + 切线脱离:重写采样循环 */
int Nsamp = qCeil(Tleft / dt);
for (int i = 0; i <= Nsamp; i++) {
double tau = i * dt; // 当前时间(s)
double tArc = tau; // 圆弧内时间(s)
int nSemi = int(tArc / Tsemi); // 第 n 个半圈
double tSemi = tArc - nSemi * Tsemi; // 半圈内时间(s)
int phase = nSemi & 3; // 0,1,2,3 只用来选圆心
/* 当前圆心 & 半径 */
double cx = 0, cy = 0;
switch (phase) {
case 0: cx = CAx; cy = CAy; break; // A 前半:entry→中点
case 1: cx = CBx; cy = CBy; break; // B 后半:中点→turn
case 2: cx = CBx; cy = CBy; break; // B 前半:turn→中点
case 3: cx = CAx; cy = CAy; break; // A 后半:中点→entry
}
/* 4 段循环:A前→B后→B前→A后→A前→...(走向相反,交叉 ∞)*/
/* ---- 起始角 ---- */
double a0 = 0;
if (phase == 0) a0 = qAtan2(ye - CAy, xe - CAx);
else if (phase == 1) a0 = qAtan2(my + CBy, mx + CBx);
else if (phase == 2) a0 = qAtan2(yt - CBy, xt - CBx);
else a0 = qAtan2(my - CAy, mx - CAx);
/* ---- 当前角度 ---- */
double ang = tSemi / Tsemi * M_PI;// 0→π(rad)
//if (!clockwise) ang = -(M_PI - ang);// B 反向:π→0,交叉 ∞
double a = a0;
if (phase == 0) {
a -= ang * cw;
}
else if (phase == 1) {
ang = -(M_PI - ang);
a += ang * cw;
}
else if (phase == 2)
{
a += ang * cw;
}
else if (phase == 3)
{
a -= ang * cw;
}
a = qAtan2(qSin(a), qCos(a)); // 正规化到 [-π,π]
/* 当前位置 & 高度 */
double x = cx + R * qCos(a); // x(m)
double y = cy + R * qSin(a); // y(m)
double h = entry.h + dHsemi * (tArc / Tsemi); // 高度线性(m)
/* 脱离判断:
当角度 ≥ 切点角,且剩余时间足够切线,则直接进入切线模式,按当前圆实时计算 */
/* ---------- 1. 当前圆切线几何 ---------- */
double OFx = xf - cx, OFy = yf - cy; // 圆→final 向量(m)
double D = hypot(OFx, OFy); // 圆心到 final 距离(m)
double alphaE = (D > R) ? qAcos(R / D) : 0.0;// 切线角(rad) cosα = R/D
double TlineNeed = qSqrt(D * D - R * R) / V; // 当前圆→final 必须切线时间
/* ---------- 2. 脱离条件 ---------- */
bool canExit = (tau >= (Tleft - TlineNeed));
if (canExit)
{
double tLine = tau - (Tleft - TlineNeed); // 直线内时间(s)
double px = x; // 脱离点 x(m)
double py = y; // 脱离点 y(m)
double ph = h; // 脱离点高度(m)
const int N = Nsamp - i + 1;
for (int j = 1; j <= N; j++) {
double k = j / double(N); // 归一化时间 0→1
double x = px + k * (xf - px); // 直线插值 x(m)
double y = py + k * (yf - py); // 直线插值 y(m)
double h = ph + k * (final.h - ph); // 直线插值 h(m)
double lat, lon;
local2ll(start.lat, start.lon, x, y, lat, lon);
path.append(WayPoint(t1 + k * tLine, lat, lon, h)); // 时间戳(s)
}
break; // 退出主循环
}
double lat, lon;
local2ll(start.lat, start.lon, x, y, lat, lon);
path.append(WayPoint(t1 + tau, lat, lon, h)); // 时间戳(s)
}
}
else if (model == TM_RUNWAY_CIRCLE_LINE) // 模式三:跑道型 = 两半圆 + 2 条正方形直边 ,先圆后直
{
/*
顺时针 顺序
边1
entry◀─────────▶p1
│ │
│ │ 边2
│ │
▼ ▼
p4◀─────────▶turn
边3
逆时针 顺序
边4
entry◀─────────▶p4
│ ▲
边1│ │ 边3
│ │
▼ │
p1◀─────────▶turn
边2
半圆 A 贴在 边1中点 外侧 → 圆心即中点
半圆 B 贴在 边3中点 外侧 → 圆心即中点
走向:
entry → A(π) → p1 → 边2 → turn → B(π) → p4 → 边4 →entry
*/
/* ---------------- 几何预计算 ---------------- */
double dx = xt - xe;
double dy = yt - ye;
double L_diag = hypot(dx, dy); // 对角线长度
double L_side = L_diag / M_SQRT2; // 正方形边长
double R = L_side * 0.5; // 半圆半径
/* 对角线单位向量 */
double ux = dx / L_diag;
double uy = dy / L_diag;
// 顺时针 45°
double s45_x = ux * M_SQRT1_2 + uy * M_SQRT1_2; // cos45·ux + sin45·uy
double s45_y = -ux * M_SQRT1_2 + uy * M_SQRT1_2; // -sin45·ux + cos45·uy
double s45_px = xe + s45_x * L_side; // 边远端
double s45_py = ye + s45_y * L_side;
// 逆时针 45°
double n45_x = ux * M_SQRT1_2 - uy * M_SQRT1_2; // cos45·ux - sin45·uy
double n45_y = ux * M_SQRT1_2 + uy * M_SQRT1_2; // sin45·ux + cos45·uy
/* 四个角点(顺时针) */
double n45_px = xe + n45_x * L_side; // 边远端
double n45_py = ye + n45_y * L_side;
double vx = 0., vy = 0.; // 边1方向
double p1x = 0., p1y = 0.; // 边1远端
double wx = 0., wy = 0.; // 边4方向
double p4x = 0., p4y = 0.; // 边4远端
if (dir == RD_CLOCKWISE)
{
vx = n45_x;
vy = n45_y;
p1x = n45_px;
p1y = n45_py;
wx = s45_x;
wy = s45_y;
p4x = s45_px;
p4y = s45_py;
}
else
{
vx = s45_x;
vy = s45_y;
p1x = s45_px;
p1y = s45_py;
wx = n45_x;
wy = n45_y;
p4x = n45_px;
p4y = n45_py;
}
/* 圆心:边1中点 与 边3中点 */
double CAx = (xe + p1x) * 0.5; // 圆 A 圆心(边1中点)
double CAy = (ye + p1y) * 0.5;
double CBx = (xt + p4x) * 0.5; // 圆 B 圆心(边3中点)
double CBy = (yt + p4y) * 0.5;
/* 两段直线方向(单位) */
/* ---------- 直线方向(用角点差一次性算对) ---------- */
double sx2 = xt - p1x; // 边2方向 p1→turn
double sy2 = yt - p1y;
double len2 = hypot(sx2, sy2); // 必 = L_side,可断言
sx2 /= len2; sy2 /= len2; // 单位化
double sx4 = xe - p4x; // 边4方向 turn→p4
double sy4 = ye - p4y;
double len4 = hypot(sx4, sy4);
sx4 /= len4; sy4 /= len4;
/* 单段耗时 */
double Tsemi = M_PI * R / V;
double Tstraight = L_side / V;
double Tloop = 2 * (Tsemi + Tstraight); // 一整圈时间
/* 每圈高度增量 */
int nLoopTot = qCeil(Tleft / Tloop);
double dHloop = (turn.h - entry.h) / nLoopTot;
/* ---------------- 采样循环 ---------------- */
int Nsamp = qCeil(Tleft / dt);
for (int i = 0; i <= Nsamp; ++i) {
double tau = i * dt;
double tRem = tau;
int nLoop = int(tau / Tloop);
tRem -= nLoop * Tloop; // 本圈剩余时间
/*顺时针 4 段顺序:entry → A(π) → p1 → 边2 → turn → B(π) → p4 → 边4 →entry*/
double cx = 0, cy = 0, a0 = 0;
double px1 = 0, py1 = 0; // 直线段起点
double px2 = 0, py2 = 0; // 直线段终点
bool inArc = true; // 当前是否圆弧
if (tRem < Tsemi) { // 段1:A 半圆
cx = CAx; cy = CAy;
a0 = qAtan2(ye - CAy, xe - CAx);
px1 = xe + vx * L_side; // 直线段起点
py1 = ye + vy * L_side;
}
else if ((tRem -= Tsemi) < Tstraight) { // 段2:边2 p1→turn
inArc = false;
px1 = p1x; py1 = p1y; // 直线起点
px2 = xt; py2 = yt; // 直线终点
}
else if ((tRem -= Tstraight) < Tsemi) { // 段3:B 半圆
cx = CBx; cy = CBy;
a0 = qAtan2(yt - CBy, xt - CBx); // 圆弧终点是 p4
px1 = p4x; py1 = p4y; // 段4起点
}
else { // 段4:边4 p4→entry
inArc = false;
tRem -= Tsemi;
px1 = p4x; py1 = p4y; // 直线起点
px2 = xe; py2 = ye; // 直线终点
}
/* ---- 当前位置 ---- */
double x = 0, y = 0, h = 0;
if (inArc) {
double ang = tRem / Tsemi * M_PI;
double a = a0 - ang*cw; // 顺时针:角度递减
x = cx + R * cos(a);
y = cy + R * sin(a);
h = entry.h + dHloop * (nLoop + tRem / Tsemi); // 圆弧内插值
}
else {
double s = tRem / Tstraight;
x = px1 + s * (px2 - px1);
y = py1 + s * (py2 - py1);
h = entry.h + dHloop * (nLoop + 0.5 + s); // 直线段插值
}
/* ---- 脱离判断(按当前圆或当前直线段实时算)---- */
double OFx = xf - x, OFy = yf - y;
double D = hypot(OFx, OFy);
double Tneed = D / V; // 当前点到 final 必须时间
bool canExit = (tau >= (Tleft - Tneed));
if (canExit) {
double s = (Tleft - tau) / Tneed; // 剩余路程比例
double px = x, py = y, ph = h;
const int N = Nsamp - i + 1;
for (int j = 1; j <= N; j++) {
double k = j / double(N); // 归一化时间 0→1
double lx = px + k * (xf - px);
double ly = py + k * (yf - py);
double lh = ph + k * (final.h - ph);
double lat, lon;
local2ll(start.lat, start.lon, lx, ly, lat, lon);
path.append(WayPoint(t1 + tau + k * (Tleft - tau), lat, lon, lh));
}
return path; // 完成,退出
}
/* ---- 正常落地 ---- */
double lat, lon;
local2ll(start.lat, start.lon, x, y, lat, lon);
path.append(WayPoint(t1 + tau, lat, lon, h));
}
}
else if (model == TM_RUNWAY_LINE_CIRCLE) // 模式四:跑道型 = 两半圆 + 2条正方形直边,先直后圆
{
/*
顺时针顺序:
边1
entry ◀──────▶ p1
│ │
│ │ 边2
│ │
▼ ▼
p4 ◀──────▶ turn
边3
逆时针顺序:
边4
entry ◀──────▶ p4
│ ▲
边1│ │边3
│ │
▼ │
p1 ◀──────▶ turn
边2
半圆A贴在边2中点外侧(圆心为边2中点)
半圆B贴在边4中点外侧(圆心为边4中点)
走向(顺时针):
entry → 边1 → p1 → A(π) → turn → 边3 → p4 → B(π) → entry
*/
/* ---------------- 几何预计算 ---------------- */
double dx = xt - xe;
double dy = yt - ye;
double L_diag = hypot(dx, dy); // 对角线长度
double L_side = L_diag / M_SQRT2; // 正方形边长
double R = L_side * 0.5; // 半圆半径
/* 对角线单位向量 */
double ux = dx / L_diag;
double uy = dy / L_diag;
// 顺时针45°方向向量
double s45_x = ux * M_SQRT1_2 + uy * M_SQRT1_2;
double s45_y = -ux * M_SQRT1_2 + uy * M_SQRT1_2;
double s45_px = xe + s45_x * L_side; // 边远端
double s45_py = ye + s45_y * L_side;
// 逆时针45°方向向量
double n45_x = ux * M_SQRT1_2 - uy * M_SQRT1_2;
double n45_y = ux * M_SQRT1_2 + uy * M_SQRT1_2;
double n45_px = xe + n45_x * L_side; // 边远端
double n45_py = ye + n45_y * L_side;
/* 四个角点(根据方向选择) */
double vx = 0., vy = 0.; // 边1方向
double p1x = 0., p1y = 0.; // 边1远端
double wx = 0., wy = 0.; // 边4方向
double p4x = 0., p4y = 0.; // 边4远端
if (dir == RD_CLOCKWISE) {
vx = n45_x; vy = n45_y;
p1x = n45_px; p1y = n45_py;
wx = s45_x; wy = s45_y;
p4x = s45_px; p4y = s45_py;
}
else {
vx = s45_x; vy = s45_y;
p1x = s45_px; p1y = s45_py;
wx = n45_x; wy = n45_y;
p4x = n45_px; p4y = n45_py;
}
/* 圆心:边2中点(半圆A) 和 边4中点(半圆B) */
double CAx = (p1x + xt) * 0.5; // 半圆A圆心(边2中点)
double CAy = (p1y + yt) * 0.5;
double CBx = (p4x + xe) * 0.5; // 半圆B圆心(边4中点)
double CBy = (p4y + ye) * 0.5;
/* 直线段方向向量(单位化) */
double sx1 = p1x - xe; // 边1方向
double sy1 = p1y - ye;
double len1 = hypot(sx1, sy1);
sx1 /= len1; sy1 /= len1;
double sx3 = p4x - xt; // 边3方向
double sy3 = p4y - yt;
double len3 = hypot(sx3, sy3);
sx3 /= len3; sy3 /= len3;
double sx4 = xe - p4x; // 边4方向
double sy4 = ye - p4y;
double len4 = hypot(sx4, sy4);
sx4 /= len4; sy4 /= len4;
/* 时间参数 */
double Tstraight = L_side / V; // 单段直线时间
double Tsemi = M_PI * R / V; // 半圆时间
double Tloop = 2 * (Tstraight + Tsemi); // 单圈总时间
/* 每圈高度增量 */
int nLoopTot = qCeil(Tleft / Tloop);
double dHloop = (turn.h - entry.h) / nLoopTot;
/* ---------------- 采样循环 ---------------- */
int Nsamp = qCeil(Tleft / dt);
for (int i = 0; i <= Nsamp; ++i) {
double tau = i * dt;
double tRem = tau;
int nLoop = static_cast<int>(tau / Tloop);
tRem -= nLoop * Tloop; // 本圈剩余时间
/* 顺时针四段顺序:边1 → 半圆A → 边3 → 半圆B */
double cx = 0, cy = 0, a0 = 0;
double px1 = 0, py1 = 0; // 直线段起点
double px2 = 0, py2 = 0; // 直线段终点
bool inArc = true; // 当前是否圆弧段
double tInSeg = tRem; // 当前段内时间
if (tRem < Tstraight) { // 段1:直线边1 (entry→p1)
inArc = false;
px1 = xe; py1 = ye;
px2 = p1x; py2 = p1y;
}
else if ((tInSeg = tRem - Tstraight) < Tsemi) { // 段2:半圆A (p1→turn)
inArc = true;
cx = CAx; cy = CAy;
a0 = qAtan2(p1y - CAy, p1x - CAx);
}
else if ((tInSeg = tRem - Tstraight - Tsemi) < Tstraight) { // 段3:直线边3 (turn→p4)
inArc = false;
px1 = xt; py1 = yt;
px2 = p4x; py2 = p4y;
}
else { // 段4:半圆B (p4→entry)
inArc = true;
tInSeg = tRem - Tstraight - Tsemi - Tstraight;
cx = CBx; cy = CBy;
a0 = qAtan2(p4y - CBy, p4x - CBx);
}
/* ---- 计算当前位置 ---- */
double x = 0, y = 0, h = 0;
if (inArc) {
// 圆弧段:角度随时间变化
double ang = tInSeg / Tsemi * M_PI;
double a = a0 - ang * cw; // 顺时针角度递减
x = cx + R * cos(a);
y = cy + R * sin(a);
// 高度插值:当前段内线性变化
h = entry.h + dHloop * (nLoop + tInSeg / Tsemi);
}
else {
// 直线段:线性插值
double s = tInSeg / Tstraight;
x = px1 + s * (px2 - px1);
y = py1 + s * (py2 - py1);
// 高度插值:段中心高度 + 偏移
h = entry.h + dHloop * (nLoop + 0.5 + s);
}
/* ---- 脱离判断(检查是否能到达终点)---- */
double OFx = xf - x, OFy = yf - y;
double D = hypot(OFx, OFy);
double Tneed = D / V; // 到达终点所需时间
bool canExit = (tau >= (Tleft - Tneed));
if (canExit) {
// 生成剩余路径点
double s = (Tleft - tau) / Tneed;
double px = x, py = y, ph = h;
const int N = Nsamp - i + 1;
for (int j = 1; j <= N; j++) {
double k = j / static_cast<double>(N);
double lx = px + k * (xf - px);
double ly = py + k * (yf - py);
double lh = ph + k * (final.h - ph);
double lat, lon;
local2ll(start.lat, start.lon, lx, ly, lat, lon);
path.append(WayPoint(t1 + tau + k * (Tleft - tau), lat, lon, lh));
}
return path; // 完成路径生成
}
/* ---- 记录常规路径点 ---- */
double lat, lon;
local2ll(start.lat, start.lon, x, y, lat, lon);
path.append(WayPoint(t1 + tau, lat, lon, h));
}
}
return path; // 完整航迹
}
// 画图窗口
class Plot : public QWidget
{
Q_OBJECT
public:
Plot(const QVector<WayPoint>& all,
const QVector<WayPoint>& four,
QWidget* parent = nullptr)
: QWidget(parent), way(all), input4(four)
{
//setFixedSize(800, 600);
setWindowTitle(u8"航迹显示");
startTime = QTime::currentTime();
QTimer* t = new QTimer(this);
connect(t, &QTimer::timeout, this, QOverload<>::of(&QWidget::update));
t->start(50); // 20 fps
}
protected:
void paintEvent(QPaintEvent*) override
{
QPainter p(this);
p.setRenderHint(QPainter::Antialiasing);
/* 1. 边界:包含生成航迹 + 4 个输入点 */
double minLat = way.first().lat, maxLat = way.first().lat;
double minLon = way.first().lon, maxLon = way.first().lon;
double minH = way.first().h, maxH = way.first().h;
for (auto& v : way) {
minLat = qMin(minLat, v.lat); maxLat = qMax(maxLat, v.lat);
minLon = qMin(minLon, v.lon); maxLon = qMax(maxLon, v.lon);
minH = qMin(minH, v.h); maxH = qMax(maxH, v.h);
}
for (auto& v : input4) {
minLat = qMin(minLat, v.lat); maxLat = qMax(maxLat, v.lat);
minLon = qMin(minLon, v.lon); maxLon = qMax(maxLon, v.lon);
minH = qMin(minH, v.h); maxH = qMax(maxH, v.h);
}
double Cx = (minLat + maxLat) / 2; // 中心纬度(rad)
double Cy = (minLon + maxLon) / 2; // 中心经度(rad)
double R = qMax(maxLat - minLat, maxLon - minLon) * 0.5; // 半跨度(rad)
/* 2. 动态尺寸 */
int W = this->width(); // 窗口总宽(px)
int H = this->height(); // 窗口总高(px)
int side = qMin(W, H); // 取短边作为参考(px)
int mapW = W / 2; // 俯视图区域宽(px) 左半
int mapH = H; // 俯视图区域高(px) 全高
int hgtW = W - mapW; // 高度图区域宽(px) 右半
int hgtH = H; // 高度图区域高(px) 全高
float scale = side / 600.0f; // 相对 600px 的缩放系数
int pointR = qBound(3, int(6 * scale), 20); // 红点半径(px)
int lineW = qBound(1, int(2 * scale), 6); // 线宽(px)
const double angle_half = 180.0; // 俯视图半宽对应角度(rad)
/* 3. 俯视图:左半区域,居中绘制 */
p.setPen(QPen(Qt::black, 1));
p.drawRect(0, 0, mapW, mapH);
p.setPen(QPen(Qt::blue, lineW));
for (int i = 1; i < way.size(); i++) {
int x1 =mapW/2 + ((way[i - 1].lon - Cy) / R * angle_half);
int y1 = mapH / 2 - ((way[i - 1].lat - Cx) / R * angle_half);
int x2 =mapW/2 + ((way[i].lon - Cy) / R * angle_half);
int y2 = mapH / 2 - ((way[i].lat - Cx) / R * angle_half);
p.drawLine(x1, y1, x2, y2);
}
// 4 个输入点
#if 0
p.setPen(Qt::NoPen);
p.setBrush(QBrush(Qt::red));
for (const auto& w : input4) {
int x = mapW / 2 + ((w.lon - Cy) / R * angle_half);
int y = mapH / 2 - ((w.lat - Cx) / R * angle_half);
p.drawEllipse(QPoint(x, y), pointR, pointR);
}
#else
p.setPen(Qt::NoPen);
QFont font = p.font();
font.setPixelSize(pointR * 3); // 字号 ≈ 3 倍圆环半径
font.setBold(true);
p.setFont(font);
int i_number = 0;
for (const auto& w : input4) {
int x = mapW / 2 + ((w.lon - Cy) / R * angle_half);
int y = mapH / 2 - ((w.lat - Cx) / R * angle_half);
/* -------- 外圈圆环 -------- */
QPainterPath ring;
ring.addEllipse(QPointF(x, y), pointR, pointR);
ring.addEllipse(QPointF(x, y), pointR * 0.6, pointR * 0.6); // 内圈挖空
p.setBrush(QBrush(Qt::red));
p.drawPath(ring);
/* -------- 序号 -------- */
p.setPen(QPen(Qt::green));
p.drawText(QRectF(x - pointR, y - pointR, pointR * 2, pointR * 2),
Qt::AlignCenter, QString::number(++i_number));
p.setPen(Qt::NoPen); // 恢复无笔
}
#endif
// 当前飞机
//double t = startTime.elapsed() / 1000.0;// 1倍速
//double t = startTime.elapsed() / 100.0;// 10倍速
double t = startTime.elapsed() / 100.;// 100倍速
if (t > way.last().t) t = way.last().t;
int idx = (t / way.last().t * (way.size() - 1));
int px =mapW/2 + ((way[idx].lon - Cy) / R * angle_half);
int py = mapH / 2 - ((way[idx].lat - Cx) / R * angle_half);
p.setBrush(Qt::red);
p.setPen(Qt::NoPen);
p.drawEllipse(px - pointR, py - pointR, 2 * pointR, 2 * pointR);
/* 4. 高度剖面:右半区域 */
p.setPen(QPen(Qt::black, 1));
p.drawRect(mapW, 0, hgtW, hgtH);
p.setPen(QPen(Qt::green, lineW));
double dx = way.last().t;
double dy = maxH - minH;
for (int i = 1; i < way.size(); i++) {
int x1 = mapW + (hgtW * way[i - 1].t / dx);
int y1 = (hgtH * 0.9 * (1.0 - (way[i - 1].h - minH) / dy) + hgtH * 0.05);
int x2 = mapW + (hgtW * way[i].t / dx);
int y2 = (hgtH * 0.9 * (1.0 - (way[i].h - minH) / dy) + hgtH * 0.05);
p.drawLine(x1, y1, x2, y2);
}
// 当前高度
int hx = mapW + (hgtW * t / dx);
int hy = (hgtH * 0.9 * (1.0 - (way[idx].h - minH) / dy) + hgtH * 0.05);
p.setBrush(Qt::red);
p.drawEllipse(hx - pointR, hy - pointR, 2 * pointR, 2 * pointR);
}
private:
QVector<WayPoint> way;
QVector<WayPoint> input4; // 仅 4 个原始点
QTime startTime;
};
cpp
#if 0
WayPoint start(0, qDegreesToRadians(39.9), qDegreesToRadians(116.4), 100);
WayPoint entry(0, qDegreesToRadians(69.5), qDegreesToRadians(101.0), 150);
WayPoint turn(0, qDegreesToRadians(49.3), qDegreesToRadians(126.2), 120);
WayPoint final(0, qDegreesToRadians(19.1), qDegreesToRadians(106.8), 80);
#else
WayPoint start(0, qDegreesToRadians(39.6), qDegreesToRadians(116.9), 150);
WayPoint entry(0, qDegreesToRadians(39.5), qDegreesToRadians(117.0), 150);
WayPoint turn(0, qDegreesToRadians(39.3), qDegreesToRadians(117.2), 120);
WayPoint final(0, qDegreesToRadians(39.4), qDegreesToRadians(116.5), 80);
#endif
/*总时间 Ttotal(s),地速 V(m/s),采样周期 dt(s)*/
double Ttotal = 1800 ;
double V = 250; // m/s
double dt = 1.0; // 输出间隔
QVector<WayPoint> w, fourPts;
{
//QVector<WayPoint> track = planDiameterCircle2(start, entry, turn, final, Ttotal, V, dt);
//QVector<WayPoint> track = planDiameterCircle2(start, entry, turn, final, Ttotal, V, dt, TM_8_CIRCLE);
//QVector<WayPoint> track = planDiameterCircle2(start, entry, turn, final, Ttotal, V, dt, TM_CIRCLE,RD_COUNTERCLOCKWISE);
#if 0
QVector<WayPoint> track = planDiameterCircle2(start, entry, turn, final, Ttotal, V, dt, TM_RUNWAY_CIRCLE_LINE, RD_CLOCKWISE);
#else
QVector<WayPoint> track = planDiameterCircle2(start, entry, turn, final, Ttotal, V, dt, TM_RUNWAY_LINE_CIRCLE, RD_CLOCKWISE);
#endif
for (auto p : track)
{
p.lat = qRadiansToDegrees(p.lat);// 转为度
p.lon = qRadiansToDegrees(p.lon);// 转为度
w.append(p);
}
QVector<WayPoint> input4= { start,entry,turn,final }; // 原始输入
for (auto p : input4)
{
p.lat = qRadiansToDegrees(p.lat);
p.lon = qRadiansToDegrees(p.lon);
fourPts.append(p);
}
}
Plot plot(w, fourPts);
plot.showMaximized();