根据前序和中序遍历构建二叉树

一、题目

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历 ， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:
复制代码
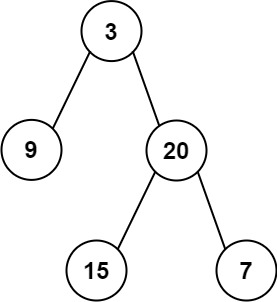
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
复制代码
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:

1 <= preorder.length <= 3000

inorder.length == preorder.length

-3000 <= preorder[i], inorder[i] <= 3000

preorder 和 inorder 均 无重复 元素

inorder 均出现在 preorder

preorder 保证为二叉树的前序遍历序列

inorder 保证为二叉树的中序遍历序列

二、源代码

objectivec 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
    if(preorderSize == 0 || inorderSize == 0)
        return NULL;
    
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    int index;
    root -> val = preorder[0];
    for(index = 0;index < inorderSize;index++)
        if(inorder[index] == preorder[0])
            break;
    root -> left = buildTree(preorder + 1,index,inorder,index);
    root -> right = buildTree(preorder + index + 1,preorderSize - index - 1,inorder + index + 1,preorderSize - index - 1);
    return root;
}

三、解题思路

递归终止条件
objectivec 复制代码
if(preorderSize == 0 || inorderSize == 0)

    return NULL;
当子树的前序 / 中序数组长度为 0 时，说明这个子树没有节点，返回NULL（比如叶子节点的左 / 右子树）。

确定根节点
objectivec 复制代码
root -> val = preorder[0];
前序遍历的第一个元素必然是当前子树的根节点，这是核心依据。

找中序数组中的根节点下标
objectivec 复制代码
for(index = 0;index < inorderSize;index++)

    if(inorder[index] == preorder[0])

        break;
(1)中序数组中，根节点左侧的所有元素都是左子树的节点；

(2)右侧的所有元素都是右子树的节点；

(3)index的值就是左子树的节点个数。

递归构建左子树
objectivec 复制代码
root -> left = buildTree(preorder + 1, index, inorder, index);
(1)preorder + 1：前序数组跳过根节点，从第二个元素开始是左子树的前序遍历；

(2)index：左子树的节点个数（中序数组中根左侧的元素数）；

(3)inorder：中序数组从开头到根节点前，都是左子树的中序遍历；

(4)最终返回的NULL或节点，作为当前根的左孩子。

递归构建右子树
objectivec 复制代码
root -> right = buildTree(preorder + index + 1, preorderSize - index - 1, inorder + index + 1, preorderSize - index - 1);
(1)preorder + index + 1：前序数组跳过根 + 左子树，剩下的是右子树的前序遍历；

(2)preorderSize - index - 1：右子树的节点个数（总节点数 - 根 - 左子树节点数）；

(3)inorder + index + 1：中序数组跳过根节点，剩下的是右子树的中序遍历；

(4)最终返回的NULL或节点，作为当前根的右孩子。

四、总结

这段代码的核心是利用前序 / 中序的遍历特性，通过递归逐层拆解子树，最终还原整个二叉树