网易ios面试题及参考答案（下）

OC 中如何实现多继承效果？如何实现面向切面编程？

OC是单继承语言（一个类仅能继承一个父类），但可通过多种方式模拟多继承效果；面向切面编程（AOP）则是将"横切逻辑"（如日志、埋点、权限校验）与业务逻辑分离，OC中可通过运行时、分类、Method Swizzling等方式实现，以下从实现方式、示例、面试要点全维度解析：

一、OC中实现多继承效果的核心方式

多继承的核心需求是"一个类拥有多个父类的属性和方法"，OC通过以下四种方式实现，优先级从高到低为：协议（Protocol）> 分类（Category）> 消息转发 > 组合/聚合。

协议（Protocol）------最常用方式

协议是OC中实现"接口继承"的核心机制，可定义方法声明，多个类可遵守同一协议，一个类可遵守多个协议，模拟多继承的"接口复用"。

基础用法 ：

复制代码

// 定义协议1
@protocol Flyable <NSObject>
- (void)fly;
@end
// 定义协议2
@protocol Runnable <NSObject>
- (void)run;
@end
// 类遵守多个协议，模拟多继承
@interface Bird : NSObject <Flyable, Runnable>
@end
@implementation Bird
- (void)fly {
    NSLog(@"Bird fly");
}
- (void)run {
    NSLog(@"Bird run");
}
@end

带默认实现的协议（OC2.0） ：OC2.0（iOS 8+/macOS 10.10+）支持协议的默认实现，通过分类实现，进一步模拟多继承的"方法复用"：

复制代码

@protocol Flyable <NSObject>
- (void)fly;
@end
// 协议分类：默认实现
@implementation NSObject (Flyable)
- (void)fly {
    NSLog(@"Default fly");
}
@end
// 类遵守协议，无需实现fly，直接使用默认实现
@interface Plane : NSObject <Flyable>
@end
@implementation Plane
// 无需实现fly
@end
// 调用
Plane *p = [[Plane alloc] init];
[p fly]; // 输出Default fly

面试要点 ：协议仅能继承方法声明，无法继承属性，需通过@property声明属性并手动实现setter/getter。

分类（Category）------方法复用

分类可向已有类添加方法，一个类可添加多个分类，模拟多继承的"方法复用"，但无法添加实例变量（可通过关联对象间接实现）。

示例（多个分类添加方法） ：

复制代码

// 分类1：Flyable
@interface NSObject (Flyable)
- (void)fly;
@end
@implementation NSObject (Flyable)
- (void)fly {
    NSLog(@"Fly");
}
@end
// 分类2：Runnable
@interface NSObject (Runnable)
- (void)run;
@end
@implementation NSObject (Runnable)
- (void)run {
    NSLog(@"Run");
}
@end
// 类使用多个分类的方法
@interface Dog : NSObject
@end
@implementation Dog
@end
// 调用
Dog *dog = [[Dog alloc] init];
[dog fly]; // 输出Fly
[dog run]; // 输出Run

关联对象添加属性 ：

复制代码

#import <objc/runtime.h>
@interface NSObject (Flyable)
@property (nonatomic, assign) int speed;
@end
@implementation NSObject (Flyable)
- (void)setSpeed:(int)speed {
    objc_setAssociatedObject(self, @selector(speed), @(speed), OBJC_ASSOCIATION_ASSIGN);
}
- (int)speed {
    return [objc_getAssociatedObject(self, @selector(speed)) intValue];
}
@end

面试要点：分类的方法优先级高于主类和父类，同名方法会覆盖主类方法（无法调用原方法，除非通过Method Swizzling）。

消息转发------行为复用

通过消息转发机制，将一个类的未实现方法转发给多个其他类，模拟多继承的"行为复用"。

示例：

复制代码

@interface A : NSObject
- (void)funcA;
@end
@implementation A
- (void)funcA {
    NSLog(@"funcA");
}
@end
@interface B : NSObject
- (void)funcB;
@end
@implementation B
- (void)funcB {
    NSLog(@"funcB");
}
@end
@interface C : NSObject
@end
@implementation C
- (id)forwardingTargetForSelector:(SEL)aSelector {
    if (aSelector == @selector(funcA)) {
        return [[A alloc] init];
    } else if (aSelector == @selector(funcB)) {
        return [[B alloc] init];
    }
    return [super forwardingTargetForSelector:aSelector];
}
@end
// 调用
C *c = [[C alloc] init];
[c funcA]; // 输出funcA
[c funcB]; // 输出funcB

组合/聚合（Composition/Aggregation）------属性复用

通过"包含其他类的实例"实现属性和方法复用，是面向对象设计中替代多继承的最佳实践（"组合优于继承"）。

示例：

复制代码

@interface FlyModule : NSObject
- (void)fly;
@property (nonatomic, assign) int flySpeed;
@end
@implementation FlyModule
- (void)fly {
    NSLog(@"Fly at speed %d", self.flySpeed);
}
@end
@interface RunModule : NSObject
- (void)run;
@property (nonatomic, assign) int runSpeed;
@end
@implementation RunModule
- (void)run {
    NSLog(@"Run at speed %d", self.runSpeed);
}
@end
// 组合多个模块，模拟多继承
@interface SuperMan : NSObject
@property (nonatomic, strong) FlyModule *flyModule;
@property (nonatomic, strong) RunModule *runModule;
- (void)fly;
- (void)run;
@end
@implementation SuperMan
- (instancetype)init {
    if (self = [super init]) {
        _flyModule = [[FlyModule alloc] init];
        _runModule = [[RunModule alloc] init];
    }
    return self;
}
- (void)fly {
    [self.flyModule fly]; // 复用FlyModule的方法
}
- (void)run {
    [self.runModule run]; // 复用RunModule的方法
}
@end
// 调用
SuperMan *man = [[SuperMan alloc] init];
man.flyModule.flySpeed = 100;
[man fly]; // 输出Fly at speed 100

面试加分点：组合方式低耦合、高扩展性，是OC中替代多继承的推荐方式，符合"开闭原则"。

二、OC中实现面向切面编程（AOP）的核心方式

AOP的核心是"在不修改原有代码的前提下，为方法添加横切逻辑"，OC中通过Method Swizzling（方法交换） 、运行时Hook 、NSProxy实现，其中Method Swizzling是最常用方式。

Method Swizzling（方法交换）------核心方式

通过OC运行时交换两个方法的实现，在原方法执行前后添加横切逻辑（如日志、埋点、性能监控）。

核心原理 ：OC的方法（Method）包含SEL（方法名）和IMP（实现指针），Method Swizzling通过method_exchangeImplementations交换两个方法的IMP。

示例（添加日志横切逻辑） ：

复制代码

#import <objc/runtime.h>
@interface UIViewController (AOP)
@end
@implementation UIViewController (AOP)
+ (void)load {
    static dispatch_once_t onceToken;
    dispatch_once(&onceToken, ^{
        // 获取原方法和自定义方法
        SEL originalSel = @selector(viewDidLoad);
        SEL swizzledSel = @selector(swizzled_viewDidLoad);
        Method originalMethod = class_getInstanceMethod(self, originalSel);
        Method swizzledMethod = class_getInstanceMethod(self, swizzledSel);
        // 交换方法实现
        method_exchangeImplementations(originalMethod, swizzledMethod);
    });
}
// 自定义方法：添加日志
- (void)swizzled_viewDidLoad {
    NSLog(@"viewDidLoad开始：%@", self.class);
    // 调用原viewDidLoad（此时已交换，实际调用swizzled_viewDidLoad）
    [self swizzled_viewDidLoad];
    NSLog(@"viewDidLoad结束：%@", self.class);
}
@end

面试要点 ：
- 必须在+load方法中实现（+load在类加载时调用，且仅调用一次）；
- 使用dispatch_once保证交换仅执行一次；
- 交换父类方法时，需注意子类是否重写该方法（避免影响子类）。

运行时Hook（Method Replacement）------替换方法实现

通过class_replaceMethod直接替换方法的IMP，实现AOP效果，与Method Swizzling的区别是"替换而非交换"。

示例：

复制代码

void newViewDidLoad(id self, SEL _cmd) {
    NSLog(@"Hook viewDidLoad");
    // 调用原实现
    Method originalMethod = class_getInstanceMethod([self class], @selector(viewDidLoad));
    IMP originalImp = method_getImplementation(originalMethod);
    originalImp(self, _cmd);
}
+ (void)load {
    SEL sel = @selector(viewDidLoad);
    Method method = class_getInstanceMethod([UIViewController class], sel);
    class_replaceMethod([UIViewController class], sel, (IMP)newViewDidLoad, method_getTypeEncoding(method));
}

NSProxy------消息转发实现AOP

NSProxy是抽象基类，可拦截所有消息并转发，通过继承NSProxy实现AOP，适用于"无侵入式"横切逻辑。

示例：

复制代码

@interface AOPProxy : NSProxy
@property (nonatomic, strong) id target;
+ (instancetype)proxyWithTarget:(id)target;
@end
@implementation AOPProxy
+ (instancetype)proxyWithTarget:(id)target {
    AOPProxy *proxy = [AOPProxy alloc];
    proxy.target = target;
    return proxy;
}
// 拦截消息
- (NSMethodSignature *)methodSignatureForSelector:(SEL)sel {
    return [self.target methodSignatureForSelector:sel];
}
- (void)forwardInvocation:(NSInvocation *)invocation {
    // 前置横切逻辑：日志
    NSLog(@"方法开始：%@", NSStringFromSelector(invocation.selector));
    // 调用原方法
    [invocation invokeWithTarget:self.target];
    // 后置横切逻辑：性能监控
    NSLog(@"方法结束：%@", NSStringFromSelector(invocation.selector));
}
@end
// 调用
UIViewController *vc = [[UIViewController alloc] init];
id proxy = [AOPProxy proxyWithTarget:vc];
[proxy viewDidLoad]; // 输出前置+后置日志

三、面试加分点

多继承 ：
- 对比各方式的优劣：协议（接口复用）、分类（方法复用）、组合（属性+方法复用，推荐）；
- 提及OC不支持多继承的原因：避免"菱形继承问题"（多个父类有同名方法，导致调用歧义）。
AOP ：
- 结合项目经验：如在埋点系统中，通过Method Swizzling拦截UIViewController的生命周期方法，自动上报页面曝光；
- 注意事项：Method Swizzling可能导致方法调用栈混乱，需添加详细日志；避免交换系统方法（如NSObject的init），防止崩溃。

记忆法推荐

多继承记忆法："协议管接口，分类加方法，组合做复用，转发补行为"；
AOP记忆法："Swizzling交换方法，Hook替换实现，NSProxy转发消息，横切逻辑无侵入"。

如何给系统类（如 UIView）新增属性？

在OC中，系统类（如UIView、UIViewController）的底层实现被封装，无法直接修改其类定义添加实例变量，但可通过分类（Category）+ 关联对象（Associated Object） 实现"新增属性"的效果，这是iOS开发中扩展系统类的核心技巧，以下从实现原理、完整示例、注意事项全维度解析：

一、核心原理：分类+关联对象

OC的分类（Category）支持为类添加方法，但不支持直接添加实例变量（编译器会报错）；关联对象是OC运行时提供的API，可将一个对象（值）与另一个对象（宿主）绑定，本质是通过全局哈希表存储"宿主对象-键-值-策略"的映射关系，从而模拟实例变量的效果。

关联对象的核心API（定义在<objc/runtime.h>）：

objc_setAssociatedObject：设置关联对象（赋值）；

复制代码

void objc_setAssociatedObject(id object, const void *key, id value, objc_AssociationPolicy policy);

objc_getAssociatedObject：获取关联对象（取值）；
复制代码
```
id objc_getAssociatedObject(id object, const void *key);
```
objc_removeAssociatedObjects：移除对象的所有关联对象（释放）。

二、完整实现示例（给UIView新增属性）

以给UIView新增customTag（字符串类型）和isHighlighted（布尔类型）属性为例，完整步骤如下：

定义分类并声明属性

// UIView+CustomProperty.h
#import <UIKit/UIKit.h>
@interface UIView (CustomProperty)
// 字符串属性：customTag
@property (nonatomic, copy) NSString *customTag;
// 布尔属性：isHighlighted
@property (nonatomic, assign) BOOL isHighlighted;
@end
实现分类并通过关联对象实现setter/getter

// UIView+CustomProperty.m
#import "UIView+CustomProperty.h"
#import <objc/runtime.h>

// 定义关联对象的key（必须唯一，通常用静态变量）
static const void *kCustomTagKey = &kCustomTagKey;
static const void *kIsHighlightedKey = &kIsHighlightedKey;

@implementation UIView (CustomProperty)

// MARK: - customTag的setter/getter
- (void)setCustomTag:(NSString *)customTag {
  // 设置关联对象：策略为OBJC_ASSOCIATION_COPY（对应copy属性）
  objc_setAssociatedObject(self, kCustomTagKey, customTag, OBJC_ASSOCIATION_COPY);
  }
- (NSString *)customTag {
  // 获取关联对象
  return objc_getAssociatedObject(self, kCustomTagKey);
  }
// MARK: - isHighlighted的setter/getter
- (void)setIsHighlighted:(BOOL)isHighlighted {
  // 布尔类型需封装为NSNumber（关联对象值必须是对象），策略为OBJC_ASSOCIATION_ASSIGN
  objc_setAssociatedObject(self, kIsHighlightedKey, @(isHighlighted), OBJC_ASSOCIATION_ASSIGN);
  }
- (BOOL)isHighlighted {
  // 取出NSNumber并转换为BOOL
  NSNumber *num = objc_getAssociatedObject(self, kIsHighlightedKey);
  return num.boolValue;
  }
@end
使用新增属性

// 调用示例
UIView *view = [[UIView alloc] init];
view.customTag = @"red_view";
view.isHighlighted = YES;

NSLog(@"customTag: %@", view.customTag); // 输出：red_view
NSLog(@"isHighlighted: %d", view.isHighlighted); // 输出：1

三、关联对象的核心策略（objc_AssociationPolicy）

关联对象的策略对应属性的内存管理语义，需与@property的修饰符匹配，核心策略如下：

策略	对应@property修饰符	核心特点
OBJC_ASSOCIATION_ASSIGN	assign	弱引用，不持有值，值销毁后变为nil（布尔/基本类型用）
OBJC_ASSOCIATION_RETAIN_NONATOMIC	strong, nonatomic	强引用，非原子性，持有值，值销毁时自动释放
OBJC_ASSOCIATION_COPY_NONATOMIC	copy, nonatomic	拷贝，非原子性，持有拷贝后的对象
OBJC_ASSOCIATION_RETAIN	strong, atomic	强引用，原子性（线程安全）
OBJC_ASSOCIATION_COPY	copy, atomic	拷贝，原子性（线程安全）

四、注意事项与面试加分点

key的唯一性：
- 必须使用静态变量作为key（如static const void *kKey = &kKey;），不能用字符串（如@"key"），避免不同分类的key冲突；
- 禁止使用NULL或随机地址作为key，会导致关联对象覆盖。
内存管理：
- 关联对象的生命周期与宿主对象一致，宿主对象释放时，关联对象会自动移除（无需手动调用objc_removeAssociatedObjects）；
- objc_removeAssociatedObjects会移除对象的所有关联对象，仅用于调试，禁止在业务代码中使用（可能移除其他分类添加的关联对象）。
基本类型处理：
- 关联对象的"值"必须是OC对象（id类型），基本类型（int、bool、float）需封装为NSNumber/NSValue后存储，取值时再转换。
面试加分点：
- 说明关联对象的底层实现：通过全局的AssociationsManager管理哈希表，每个对象对应一个AssociationsHashMap，存储key和关联对象的映射；
- 提及性能问题：关联对象的存取性能略低于实例变量，但在日常开发中可忽略；
- 结合项目经验：如在自定义埋点系统中，给UIButton新增trackID属性，用于标记点击埋点的唯一标识。

五、常见错误场景

直接在分类中声明实例变量：@interface UIView (CustomProperty) { NSString *_customTag; } @end------编译器报错，分类不支持实例变量；
策略与属性修饰符不匹配：如copy属性使用OBJC_ASSOCIATION_RETAIN_NONATOMIC------导致对象未拷贝，违反属性语义；
使用临时变量作为key：objc_setAssociatedObject(self, @"key", value, ...)------不同分类用相同字符串key会覆盖关联对象。

记忆法推荐

核心步骤记忆法：给系统类新增属性记住"三步法"------分类声明属性→静态变量定义key→关联对象实现setter/getter；
策略匹配记忆法："assign对应ASSIGN，strong对应RETAIN，copy对应COPY，原子性加ATOMIC"。

请对比 OC 中 load 方法与 initialize 方法的区别

OC中的+load和+initialize是类加载和初始化阶段的两个特殊类方法，均由运行时自动调用，但在调用时机、调用时机、调用次数、调用顺序、使用场景等核心维度存在本质差异，是iOS面试中考察OC运行时原理的高频考点。

一、核心区别全维度解析

维度	+load 方法	+initialize 方法
调用时机	类/分类被加载到内存时（程序启动阶段，dyld加载镜像后）	类第一次收到消息时（延迟调用，懒加载）
调用次数	仅调用一次（类加载时），分类的load会覆盖吗？→ 不会，类和分类的load都会调用	仅调用一次（类第一次使用时），若子类未实现，会调用父类的initialize（可能多次触发父类调用）
调用顺序	1. 父类 → 子类；2. 类 → 分类（分类的load后调用）；3. 多个分类按编译顺序调用	1. 父类 → 子类；2. 仅调用类的initialize，分类的initialize会覆盖类的实现
调用条件	无论是否使用类，只要加载就调用（强制调用）	仅当类被使用时调用（如创建实例、调用类方法），未使用则不调用
线程安全	调用时处于主线程，且没有自动释放池，需手动管理内存	调用时由运行时加锁，线程安全，但耗时操作会阻塞线程
能否主动调用	不建议主动调用（违反设计初衷，可能导致逻辑混乱）	可主动调用，但无意义（运行时已保证仅调用一次）
使用场景	Method Swizzling、初始化全局变量、注册通知（必须提前执行的逻辑）	初始化类的静态变量、懒加载类配置（延迟执行的初始化逻辑）

二、调用时机与顺序的详细说明

+load 方法的调用规则

类的load ：当类的二进制文件（.o）被dyld加载到内存时，运行时会遍历所有类，按"父类→子类"的顺序调用+load；
分类的load ：类的load调用完成后，按分类的编译顺序（Build Phases → Compile Sources中的顺序）调用分类的+load，且分类的+load不会覆盖类的+load；

示例验证 ：

复制代码

// 父类
@interface Parent : NSObject
@end
@implementation Parent
+ (void)load {
    NSLog(@"Parent load");
}
@end

// 子类
@interface Child : Parent
@end
@implementation Child
+ (void)load {
    NSLog(@"Child load");
}
@end

// 子类分类1
@interface Child (Category1)
@end
@implementation Child (Category1)
+ (void)load {
    NSLog(@"Child Category1 load");
}
@end

// 子类分类2
@interface Child (Category2)
@end
@implementation Child (Category2)
+ (void)load {
    NSLog(@"Child Category2 load");
}
@end

输出顺序 ：

复制代码

Parent load
Child load
Child Category1 load // 编译顺序靠前
Child Category2 load // 编译顺序靠后

+initialize 方法的调用规则

懒加载调用 ：仅当类第一次收到消息（如[Child new]、[Child classMethod]）时调用，未使用则不调用；
父类优先：子类调用initialize前，会先调用父类的initialize（即使父类未被使用）；
分类覆盖：若分类实现了initialize，会覆盖类的initialize（仅调用分类的实现）；

父类多次触发 ：若子类未实现initialize，子类第一次使用时会调用父类的initialize，多个子类未实现时，父类的initialize会被多次调用；示例验证 ：

复制代码

// 父类
@implementation Parent
+ (void)initialize {
    NSLog(@"Parent initialize: %@", self);
}
@end

// 子类1（未实现initialize）
@interface Child1 : Parent
@end
@implementation Child1
@end

// 子类2（未实现initialize）
@interface Child2 : Parent
@end
@implementation Child2
@end

// 调用
[Child1 new];
[Child2 new];

输出：

复制代码

Parent initialize: Child1 // Child1触发父类initialize，self为Child1
Parent initialize: Child2 // Child2触发父类initialize，self为Child2

若子类实现initialize：

复制代码

@implementation Child1
+ (void)initialize {
    NSLog(@"Child1 initialize");
}
@end

输出：

复制代码

Parent initialize: Parent // Child1触发父类initialize，self为Parent
Child1 initialize
Parent initialize: Child2 // Child2触发父类initialize，self为Child2

三、使用场景与面试易错点

+load 的典型场景

Method Swizzling ：必须在+load中实现（类加载时完成方法交换，保证后续调用生效）；

复制代码

+ (void)load {
    static dispatch_once_t onceToken;
    dispatch_once(&onceToken, ^{
        // 方法交换逻辑
    });
}

全局初始化：如注册全局通知、初始化静态库配置（程序启动时必须执行的逻辑）；
注意：+load中不能使用[self class]或self调用其他方法（可能类未初始化完成），且无自动释放池，需手动管理内存（如创建autoreleasepool）。

+initialize 的典型场景

类静态变量初始化 ：如初始化类的静态缓存、配置参数（延迟初始化，节省启动时间）；

复制代码

static NSMutableDictionary *cache;
+ (void)initialize {
    if (self == [MyClass class]) { // 防止子类触发多次初始化
        cache = [NSMutableDictionary dictionary];
    }
}

懒加载配置：如加载类的默认样式、初始化网络请求配置（类第一次使用时执行）；
注意：需判断self == [本类 class]，避免子类触发父类的initialize多次执行。

面试易错点

认为+load中分类的实现会覆盖类的实现：错误，类和分类的+load都会调用，顺序为类→分类；
认为+initialize仅调用一次：错误，若子类未实现，父类的+initialize会被多个子类触发多次；
混淆调用时机：+load是程序启动时调用，+initialize是类第一次使用时调用；
在+load中执行耗时操作：导致程序启动时间延长，违反性能优化原则。

四、面试加分点

说明底层实现：+load由dyld触发objc_load_images函数调用，+initialize由objc_msgSend触发，当类第一次接收消息时，运行时检查是否已调用initialize，未调用则先调用；
性能优化：+load中的逻辑应尽量精简（影响启动时间），+initialize适合延迟初始化（优化启动速度）；
线程安全：+load在主线程调用，无锁；+initialize由运行时加锁（runtimeLock），线程安全，但耗时操作会阻塞其他线程调用该类。

记忆法推荐

核心特征记忆法 ：+load记住"加载时、强制调、类+分类都执行、一次调用"；+initialize记住"使用时、延迟调、分类覆盖类、父类可能多次调"；
使用场景记忆法："load做交换（Method Swizzling），initialize做初始化（静态变量）"。

请详细阐述 OC 中 autoreleasepool 的使用方式、底层原理及底层数据结构；autoreleasepool 的 pop、push 方法是否会影响对象的引用计数？

autoreleasepool（自动释放池）是OC内存管理的核心机制，用于延迟释放对象（将对象的release操作延迟到释放池销毁时执行），其底层基于编译器和运行时的协作实现，是iOS面试中考察内存管理的重中之重。

一、autoreleasepool 的使用方式

基本使用方式

手动创建（MRC/ARC） ：

复制代码

// 方式1：NSAutoreleasePool（MRC，ARC中已废弃）
NSAutoreleasePool *pool = [[NSAutoreleasePool alloc] init];
// 创建autorelease对象
NSString *str = [[[NSString alloc] initWithFormat:@"test"] autorelease];
[pool drain]; // MRC释放池，ARC中用[pool release]（但不推荐）

// 方式2：@autoreleasepool（ARC/MRC推荐，编译器优化）
@autoreleasepool {
    // 代码块内的autorelease对象会加入当前释放池
    NSString *str = [NSString stringWithFormat:@"test"]; // 自动加入释放池
    UIView *view = [[UIView alloc] init];
    [view autorelease]; // 手动加入释放池（MRC）
} // 释放池销毁，所有对象调用release

隐式创建：iOS程序运行时，主线程的RunLoop会自动创建和销毁autoreleasepool（每次事件循环迭代时，创建新池，处理完事件后销毁），因此主线程的autorelease对象无需手动创建释放池。

嵌套使用

autoreleasepool支持嵌套，内层池销毁时仅释放内层池中的对象，外层池销毁时释放外层池中的对象：

复制代码

@autoreleasepool { // 外层池
    NSString *str1 = [NSString stringWithFormat:@"outer"];
    @autoreleasepool { // 内层池
        NSString *str2 = [NSString stringWithFormat:@"inner"];
    } // 内层池销毁，str2调用release
} // 外层池销毁，str1调用release

多线程使用

每个线程有独立的autoreleasepool栈，子线程中若创建大量autorelease对象，需手动创建释放池，否则对象会累积到线程退出时释放，导致内存峰值过高：

复制代码

dispatch_async(dispatch_get_global_queue(0, 0), ^{
    @autoreleasepool {
        // 子线程中创建大量autorelease对象
        for (int i=0; i<10000; i++) {
            NSString *str = [NSString stringWithFormat:@"%d", i];
        }
    } // 释放池销毁，批量释放对象
});

二、autoreleasepool 的底层原理

编译器层面的转换

@autoreleasepool { ... } 是编译器语法糖，会被转换为以下代码（伪代码）：

复制代码

void *ctx = objc_autoreleasePoolPush(); // 创建释放池（push）
@try {
    // 代码块逻辑
} @finally {
    objc_autoreleasePoolPop(ctx); // 销毁释放池（pop）
}

核心是objc_autoreleasePoolPush（入栈）和objc_autoreleasePoolPop（出栈）两个运行时函数。

运行时层面的核心逻辑

autorelease对象的加入 ：对象调用autorelease方法时，运行时会将对象添加到当前线程的"当前autoreleasepool"中，autorelease的核心实现：

复制代码

- (id)autorelease {
    return objc_autorelease(self);
}
id objc_autorelease(id obj) {
    if (!obj) return obj;
    // 获取当前线程的autoreleasepool，将对象加入
    return objc_autoreleasePoolAddObject(obj);
}

释放池的销毁（pop） ：objc_autoreleasePoolPop调用时，遍历当前释放池中的所有对象，调用release方法，然后销毁释放池。

核心规则

autorelease对象的释放时机：释放池pop时（而非对象超出作用域时）；
引用计数变化：对象调用autorelease时，引用计数不变化（仅标记需延迟释放）；释放池pop时，对象调用release，引用计数-1；
线程独立性：每个线程有独立的autoreleasepool栈，对象仅加入当前线程的释放池。

三、autoreleasepool 的底层数据结构

autoreleasepool的底层基于线程局部存储（TLS）+ 双向链表 + 页结构（AutoreleasePoolPage） 实现：

AutoreleasePoolPage 结构体

这是autoreleasepool的核心数据结构（定义在objc4源码中），核心字段：

复制代码

class AutoreleasePoolPage {
    magic_t const magic; // 校验页的完整性
    id *next; // 指向下一个可存储autorelease对象的位置
    pthread_t const thread; // 所属线程
    AutoreleasePoolPage *const parent; // 父页（链表前向指针）
    AutoreleasePoolPage *child; // 子页（链表后向指针）
    uint32_t const depth; // 页的深度（链表层级）
    uint32_t hiwat; // 高水位标记
    // 存储autorelease对象的数组（4096字节，除开上述字段，剩余空间存储对象）
    id obj[0];
};

每个AutoreleasePoolPage大小为4096字节（一页内存）；
多个页通过parent和child组成双向链表；
next指针指向数组中未使用的位置，添加对象时next++，pop时next--并调用release。

释放池栈的管理

push操作 ：调用objc_autoreleasePoolPush时，运行时会在当前线程的AutoreleasePoolPage链表中创建一个"哨兵对象（POOL_SENTINEL）"，作为释放池的边界标记，返回该哨兵对象的地址；
add操作 ：对象调用autorelease时，运行时找到当前线程的最后一个AutoreleasePoolPage，若页未满，将对象存储到next位置，next++；若页已满，创建新页，添加到链表尾部，再存储对象；
pop操作 ：调用objc_autoreleasepoolPop(ctx)时，ctx是哨兵对象的地址，运行时从最后一个页的next位置向前遍历，直到找到哨兵对象，遍历过程中对每个对象调用release，然后将next指针重置为哨兵对象的位置。

四、pop/push 方法是否影响对象的引用计数？

push 方法

objc_autoreleasePoolPush（push操作）仅创建释放池的边界标记（哨兵对象），不涉及任何对象的引用计数变化。

pop 方法

objc_autoreleasePoolPop（pop操作）会遍历释放池中的所有autorelease对象，调用release方法，导致对象的引用计数-1：

若对象的引用计数变为0，对象会被销毁（调用dealloc）；
若对象的引用计数仍大于0，对象不会被销毁（仅减少计数）。

关键补充

对象调用autorelease时，引用计数不变化（仅标记加入释放池）；
释放池的核心作用是"延迟执行release"，而非改变引用计数的最终结果；

示例验证（MRC）：

复制代码

NSObject *obj = [[NSObject alloc] init];
NSLog(@"retain count: %ld", [obj retainCount]); // 1
[obj autorelease];
NSLog(@"retain count: %ld", [obj retainCount]); // 1（autorelease不改变计数）
@autoreleasepool {
    // 空池，仅演示pop
} // pop时调用release，计数-1 → 0，对象销毁

五、面试加分点与易错点

面试加分点

结合objc4源码说明AutoreleasePoolPage的结构：4096字节、双向链表、哨兵对象；
性能优化：大量创建autorelease对象时（如循环创建字符串），应在循环内部创建小的autoreleasepool，避免单个池累积过多对象导致内存峰值；
复制代码
```
for (int i=0; i<10000; i++) {
    @autoreleasepool {
        NSString *str = [NSString stringWithFormat:@"%d", i];
    } // 每次循环销毁池，及时释放对象
}
```
主线程RunLoop与autoreleasepool：主线程RunLoop的kCFRunLoopBeforeWaiting和kCFRunLoopAfterWaiting阶段会创建/销毁autoreleasepool，保证每次事件循环后释放对象。

易错点

认为autoreleasepool会增加对象的引用计数：错误，autorelease仅延迟release，不改变计数；
认为pop操作会销毁对象：错误，pop仅调用release，对象是否销毁取决于引用计数是否为0；
子线程中不创建autoreleasepool：导致autorelease对象累积到线程退出时释放，内存峰值过高。

记忆法推荐

核心原理记忆法：autoreleasepool记住"三要素"------页结构（AutoreleasePoolPage）、链表管理、哨兵对象；
引用计数记忆法："push不计数，autorelease不计数，pop调release才减计数"。

请对比 OC 中 weak 与 assign 修饰符的核心区别

weak和assign是OC中用于修饰变量的弱引用修饰符，均不会增加对象的引用计数，但在内存管理语义、空指针安全、适用场景等核心维度存在本质差异，是iOS面试中考察内存管理的高频考点。

一、核心区别全维度解析

维度	weak 修饰符	assign 修饰符
内存管理语义	弱引用，对象销毁时自动置为nil（空指针安全）	弱引用，对象销毁时不置为nil（悬垂指针，野指针风险）
适用类型	仅适用于OC对象（如NSObject、UIView、NSString等）	适用于基本数据类型（int、float、bool）+ OC对象（不推荐）
引用计数影响	不增加对象的引用计数	不增加对象的引用计数
空指针安全	安全，访问nil对象不会崩溃（OC消息发送nil无响应）	不安全，访问悬垂指针会导致崩溃（EXC_BAD_ACCESS）
运行时处理	由Runtime维护弱引用表，对象销毁时自动清理	无运行时处理，仅简单赋值
原子性	可搭配atomic（`weak atomic`），但iOS 10+后atomic对weak无效	可搭配atomic（`assign atomic`），保证赋值的原子性
循环引用	解决循环引用（如block、delegate）	无法解决循环引用（对象销毁后指针悬空）

二、核心差异的详细说明

内存管理语义（最核心区别）

weak 修饰符 ：weak修饰的OC对象指针，会被Runtime加入"弱引用表"（Weak Reference Table），当对象的引用计数变为0（即将销毁）时，Runtime会遍历弱引用表，将所有指向该对象的weak指针自动置为nil。示例验证：

复制代码

NSObject *obj = [[NSObject alloc] init];
__weak NSObject *weakObj = obj;
NSLog(@"weakObj before release: %@", weakObj); // 输出对象地址
obj = nil; // 释放obj，引用计数变为0，对象销毁
NSLog(@"weakObj after release: %@", weakObj); // 输出nil
[weakObj performSelector:@selector(description)]; // 调用nil的方法，无崩溃

assign 修饰符 ：assign修饰的OC对象指针，仅做简单的赋值操作，不参与Runtime的弱引用管理。当对象销毁后，指针仍指向原内存地址（悬垂指针），访问该指针会导致野指针崩溃。示例验证：

复制代码

NSObject *obj = [[NSObject alloc] init];
__unsafe_unretained NSObject *assignObj = obj; // assign等价于__unsafe_unretained
NSLog(@"assignObj before release: %@", assignObj); // 输出对象地址
obj = nil; // 释放obj，对象销毁
NSLog(@"assignObj after release: %@", assignObj); // 输出原地址（悬空）
[assignObj performSelector:@selector(description)]; // 崩溃：EXC_BAD_ACCESS

注：在ARC中，assign修饰OC对象时，编译器会警告，推荐使用__unsafe_unretained（语义等价）。

适用场景

weak 的典型场景：

delegate/代理：避免代理对象与被代理对象循环引用；

复制代码

@protocol MyDelegate <NSObject>
@end
@interface MyClass : NSObject
@property (nonatomic, weak) id<MyDelegate> delegate; // 弱引用代理
@end

block中的外部对象：避免block捕获对象导致循环引用；

复制代码

__weak typeof(self) weakSelf = self;
self.block = ^{
    __strong typeof(weakSelf) strongSelf = weakSelf;
    if (strongSelf) {
        // 使用strongSelf
    }
};

临时引用对象：如UI控件的临时引用（无需持有，仅访问）。

assign 的典型场景：
- 基本数据类型：int、float、bool、CGFloat、NSInteger等；
  复制代码
```
@interface MyView : UIView
@property (nonatomic, assign) CGFloat width; // 基本类型用assign
@property (nonatomic, assign) BOOL isSelected;
@end
```
- C语言结构体/枚举：如CGRect、UIEdgeInsets、UIStatusBarStyle等；
  复制代码
```
@property (nonatomic, assign) CGRect frame;
@property (nonatomic, assign) UIStatusBarStyle statusBarStyle;
```
- 绝对不推荐用于OC对象（除非明确接受野指针风险）。

运行时底层实现

weak 的底层：Runtime维护三张核心表：
1. 弱引用表（Weak Reference Table）：存储"对象地址→weak指针数组"的映射；
2. 引用计数表（Retain Count Table）：存储对象的引用计数；
3. 哈希表（Side Table）：关联上述两张表。当对象调用dealloc时，Runtime会：
- 从弱引用表中取出所有指向该对象的weak指针；
- 将这些指针置为nil；
- 从弱引用表中移除该对象的条目。
assign 的底层 ：无任何Runtime处理，仅为编译器层面的赋值语义，等价于C语言的直接赋值（ptr = obj），对象销毁后指针不会被修改。

三、面试易错点与加分点

易错点

认为weak和assign都能解决循环引用：错误，assign修饰OC对象时，对象销毁后指针悬空，无法解决循环引用（仅weak能自动置nil）；
认为weak可以修饰基本数据类型：错误，weak仅适用于OC对象，基本类型必须用assign；
混淆__weak和__unsafe_unretained：__weak是安全的弱引用（自动置nil），__unsafe_unretained是不安全的弱引用（等价于assign，指针悬空）；
认为weak的atomic修饰符有效：iOS 10之后，Runtime不再保证weak的atomic语义，weak atomic等价于weak nonatomic。

加分点

结合objc4源码说明weak的实现：objc_storeWeak（设置weak指针）、objc_destroyWeak（销毁weak指针）、objc_dealloc中清理弱引用表；
性能对比：weak的赋值和销毁有Runtime开销（维护弱引用表），assign无开销（仅赋值），因此基本类型优先用assign；
循环引用的完整解决方案：delegate用weak、block用weak-strong dance、NSTimer用weak+中间对象。

四、补充说明（ARC中的语义）

在ARC中，修饰符的语义规则：

strong：强引用，增加引用计数，对象销毁时自动release；
weak：弱引用，不增加计数，对象销毁时自动置nil；
assign：仅适用于非对象类型，对象类型用__unsafe_unretained；
copy：拷贝对象，强引用拷贝后的对象；
retain：MRC中的强引用，ARC中等价于strong。

记忆法推荐

核心区别记忆法："weak管对象，自动置nil保安全；assign管基本，对象用它必悬空"；
适用场景记忆法："weak用在代理和block，assign用在int和float"。

NSNotificationCenter 的消息发送和接收是否在同一个线程？消息发送是同步还是异步？接收消息的同步 / 异步性如何？

NSNotificationCenter（通知中心）是OC中实现跨组件通信的核心机制，其消息发送（postNotification）和接收（addObserver）的线程、同步/异步特性，直接影响代码的线程安全和执行逻辑，是iOS面试中考察多线程和通知机制的高频考点。

一、核心结论（先明确答案）

线程一致性 ：消息发送和接收默认在同一个线程（发送消息的线程）；
发送的同步性 ：消息发送（postNotification）是同步操作；
接收的同步性：默认与发送同步（接收方在发送线程同步执行），可通过自定义队列实现异步接收。

二、详细解析：线程模型

消息发送和接收的线程规则

NSNotificationCenter本身不维护线程，通知的接收线程完全由发送线程决定：

若在主线程调用[[NSNotificationCenter defaultCenter] postNotificationName:...]，则所有观察者的selector/block在主线程执行；
若在子线程调用postNotification，则所有观察者的处理逻辑在该子线程执行；
观察者注册时指定的线程（如通过NSNotificationQueue）不影响接收线程，仅影响执行时机。

示例验证：

复制代码

// 注册观察者（主线程）
[[NSNotificationCenter defaultCenter] addObserverForName:@"TestNotification"
                                                  object:nil
                                                   queue:nil
                                              usingBlock:^(NSNotification * _Nonnull note) {
    NSLog(@"接收线程：%@", [NSThread currentThread]);
}];

// 子线程发送通知
dispatch_async(dispatch_get_global_queue(0, 0), ^{
    NSLog(@"发送线程：%@", [NSThread currentThread]);
    [[NSNotificationCenter defaultCenter] postNotificationName:@"TestNotification" object:nil];
});

输出：

复制代码

发送线程：<NSThread: 0x60000381c000>{number = 3, name = (null)}
接收线程：<NSThread: 0x60000381c000>{number = 3, name = (null)}

（接收线程与发送线程一致，均为子线程）

特殊场景：NSNotificationQueue（通知队列）

NSNotificationQueue是基于NSNotificationCenter的异步通知队列，可将通知加入队列，延迟发送（异步），但接收线程仍为队列指定的线程：

NSPostASAP：尽快在当前线程的RunLoop空闲时发送；
NSPostWhenIdle：在RunLoop空闲时发送；
NSPostNow：立即发送（同步，等价于直接post）。

示例：

复制代码

// 获取当前线程的通知队列
NSNotificationQueue *queue = [NSNotificationQueue defaultQueue];
// 创建通知
NSNotification *note = [NSNotification notificationWithName:@"TestNotification" object:nil];
// 异步发送（加入队列，RunLoop空闲时发送）
[queue enqueueNotification:note postingStyle:NSPostASAP];

说明：通知仍在当前线程的RunLoop中执行，仅延迟发送，接收线程不变。

三、详细解析：同步/异步特性

消息发送的同步性

postNotification（包括postNotificationName:object:/postNotificationName:object:userInfo:）是同步操作：

调用postNotification后，会立即遍历所有注册的观察者，依次调用观察者的处理逻辑（selector/block）；
所有观察者的逻辑执行完成后，postNotification才会返回；
若某个观察者的处理逻辑耗时（如网络请求、大量计算），会阻塞发送线程（主线程发送则卡顿，子线程发送则阻塞子线程）。

示例验证：

复制代码

// 注册耗时观察者
[[NSNotificationCenter defaultCenter] addObserver:self
                                         selector:@selector(handleNotification:)
                                             name:@"TestNotification"
                                           object:nil];

- (void)handleNotification:(NSNotification *)note {
    NSLog(@"开始处理通知");
    [NSThread sleepForTimeInterval:2]; // 耗时2秒
    NSLog(@"处理完成");
}

// 主线程发送通知
NSLog(@"开始发送通知");
[[NSNotificationCenter defaultCenter] postNotificationName:@"TestNotification" object:nil];
NSLog(@"发送完成");

输出顺序：

复制代码

开始发送通知
开始处理通知
处理完成
发送完成

（发送操作阻塞，直到处理完成才返回）

接收消息的同步/异步控制

默认情况下，接收消息是同步的（与发送同步），但可通过以下方式实现异步接收：

方式1：观察者处理逻辑中异步执行

在观察者的selector/block中，将耗时逻辑dispatch到其他队列，避免阻塞发送线程：

复制代码

- (void)handleNotification:(NSNotification *)note {
    // 异步处理耗时逻辑
    dispatch_async(dispatch_get_global_queue(0, 0), ^{
        [NSThread sleepForTimeInterval:2];
        NSLog(@"异步处理完成");
    });
}

输出顺序：

复制代码

开始发送通知
开始处理通知
发送完成
异步处理完成

（发送操作不再阻塞，接收逻辑异步执行）

方式2：注册时指定自定义队列（iOS 4.0+）

addObserverForName:object:queue:usingBlock:方法的queue参数，可指定观察者的处理队列：

若queue为nil：处理逻辑在发送线程执行（默认）；
若queue为自定义队列（如全局并发队列、串行队列）：处理逻辑在该队列执行（异步）。

示例：

复制代码

// 注册时指定全局并发队列
NSOperationQueue *queue = [NSOperationQueue new];
queue.underlyingQueue = dispatch_get_global_queue(0, 0);

[[NSNotificationCenter defaultCenter] addObserverForName:@"TestNotification"
                                                  object:nil
                                                   queue:queue
                                              usingBlock:^(NSNotification * _Nonnull note) {
    NSLog(@"接收线程：%@", [NSThread currentThread]);
    [NSThread sleepForTimeInterval:2];
}];

// 主线程发送通知
NSLog(@"开始发送通知");
[[NSNotificationCenter defaultCenter] postNotificationName:@"TestNotification" object:nil];
NSLog(@"发送完成");

输出顺序：

复制代码

开始发送通知
发送完成
接收线程：<NSThread: 0x60000381c000>{number = 3, name = (null)}

（发送操作同步返回，接收逻辑在指定队列异步执行）

四、面试易错点与加分点

易错点

认为通知的接收线程是主线程：错误，接收线程由发送线程决定，仅当在主线程post时接收线程才是主线程；
认为postNotification是异步操作：错误，post是同步操作，会阻塞直到所有观察者处理完成；
认为addObserverForName:queue:的queue参数改变发送线程：错误，queue仅指定接收逻辑的执行队列，发送线程不变；
通知的线程安全问题：若多个线程发送同一通知，观察者的处理逻辑需保证线程安全（如加锁、使用原子属性）。

加分点

通知的注销时机：ARC中，addObserverForName:queue:usingBlock:返回的id需手动注销（removeObserver:），否则会导致内存泄漏；addObserver:selector:name:object:在对象销毁时自动注销（但仍建议手动注销）；
通知的重复发送：若多次注册同一观察者，会多次接收通知，需保证注册/注销成对；
性能优化：大量发送通知时，避免在主线程post耗时通知，可通过NSNotificationQueue延迟发送，或异步处理接收逻辑；
替代方案：通知中心是同步的一对多通信，若需异步、一对一通信，可使用代理、Block、回调、RAC（ReactiveCocoa）等。

五、总结（核心规则）

线程：接收线程 = 发送线程（默认），可通过queue参数指定接收队列；
发送：post是同步操作，阻塞直到所有观察者处理完成；
接收：默认同步，可通过异步队列实现异步接收；
线程安全：观察者处理逻辑需保证线程安全（多线程post时）。

记忆法推荐

核心规则记忆法："通知发送同步走，接收线程跟发送；要想异步不阻塞，队列指定或异步"；
易错点记忆法："主线程接收是特例，post同步会阻塞，queue改队列不改线程"。

Weex 与 Native（原生）之间如何实现通讯？

Weex 作为跨端框架，其核心能力之一是实现 JS 层（Weex 前端）与 Native 层（iOS/Android 原生）的双向通信，通信的核心载体是 JSBridge，底层依赖各平台的 JS 引擎（iOS：ScriptCore；Android：V8/JSC），通信模式分为"JS 调用原生"和"原生调用 JS"两类，以下从通信原理、具体实现、扩展能力三方面详细说明：

一、通信核心基础：JSBridge 与 JS 引擎

JSBridge 是连接 JS 层与 Native 层的"桥梁"，本质是一套通信协议，负责将 JS 指令转换为原生可识别的格式，同时将原生的回调/事件转换为 JS 可执行的代码。

iOS 端 JS 引擎 ：基于 ScriptCore 框架（苹果官方），提供 JSContext（JS 执行上下文）、JSValue（JS 与 OC 数据类型转换）核心类，支持同步/异步通信；
Android 端 JS 引擎 ：默认使用 JSC（ScriptCore），也可替换为 V8 引擎，二者均支持 JS 与的双向绑定。

二、通信模式1：JS 调用 Native（前端触发，原生执行）

JS 调用 Native 是最常用的场景（如调用原生的 Toast、分享、支付等能力），Weex 封装了标准化的调用方式，核心分为"内置模块调用"和"自定义模块调用"。

内置模块调用（Weex 原生支持）

Weex 内置了常用的原生模块（如 modal、navigator、stream），JS 可直接通过 weex.requireModule 调用，无需原生额外开发。

复制代码

// JS 层调用原生 Toast（内置 modal 模块）
const modal = weex.requireModule('modal');
modal.toast({
  message: 'JS 调用原生 Toast',
  duration: 2 // 显示时长
});

// JS 层调用原生导航（内置 navigator 模块）
const navigator = weex.requireModule('navigator');
navigator.push({
  url: 'native_page.js', // 跳转的 Weex 页面
  animated: 'true'
});

iOS 端底层实现逻辑：

Weex 初始化时，会将内置模块（如 WXModalModule）注册到 JSContext 中；
JS 调用 modal.toast 时，JSContext 触发 OC 方法 -[WXModalModule toast:]；
OC 方法接收 JS 传递的参数（JSON 格式），解析后调用 UIAlertController 显示 Toast。

自定义模块调用（扩展原生能力）

若内置模块无法满足需求，可自定义原生模块，步骤如下（以 iOS 为例）：

步骤1：iOS 端自定义 OC 模块

复制代码

// 1. 导入 Weex 头文件
#import <WeexSDK/WXSDKInstance.h>
#import <WeexSDK/WXModuleProtocol.h>

// 2. 定义自定义模块，遵守 WXModuleProtocol 协议
@interface WXCustomModule : NSObject <WXModuleProtocol>
@end

@implementation WXCustomModule

// 3. 暴露方法给 JS（必须加 WX_EXPORT_METHOD 宏）
WX_EXPORT_METHOD(@selector(customMethod:callback:))
- (void)customMethod:(NSDictionary *)params callback:(WXModuleCallback)callback {
    // 解析 JS 传递的参数
    NSString *content = params[@"content"];
    NSLog(@"JS 传递的参数：%@", content);
    
    // 执行原生逻辑（如获取设备信息）
    NSString *deviceId = [[UIDevice currentDevice] identifierForVendor].UUIDString;
    NSDictionary *result = @{@"deviceId": deviceId, @"code": 200};
    
    // 回调 JS（将结果返回）
    if (callback) {
        callback(result);
    }
}

@end

// 4. 注册自定义模块（AppDelegate 中）
[WXSDKEngine registerModule:@"customModule" withClass:[WXCustomModule class]];

步骤2：JS 层调用自定义模块

复制代码

// 1. 引入自定义模块
const customModule = weex.requireModule('customModule');

// 2. 调用自定义方法，传递参数并接收回调
customModule.customMethod({
  content: 'JS 调用自定义原生模块'
}, (result) => {
  console.log('原生返回的结果：', result);
  // 输出：{ deviceId: "xxx", code: 200 }
});

关键细节：参数传递与数据类型转换

参数格式：JS 传递给原生的参数为 JSON 格式（对象/数组），原生解析为 NSDictionary/NSArray；

数据类型映射 ：

JS 类型	iOS OC 类型	Android 类型
Number	NSNumber	int/float/double
String	NSString	String
Boolean	NSNumber	boolean
Object	NSDictionary	Map
Array	NSArray	List
Function	WXModuleCallback	Callback

异步回调 ：JS 传递的回调函数在原生中对应 WXModuleCallback（iOS）/ JSCallback（Android），原生执行完逻辑后调用回调，将结果返回 JS。

三、通信模式2：Native 调用 JS（原生触发，前端执行）

原生调用 JS 用于"原生事件通知 JS"（如原生页面返回、设备网络状态变化），核心方式是"执行 JS 代码片段"或"调用 JS 方法"。

iOS 端原生调用 JS 方法

// 1. 获取 Weex 实例的 JSContext
JSContext *jsContext = self.weexInstance.jsContext;

// 2. 方式1：直接执行 JS 代码片段
NSString *jsCode = @"console.log('原生调用 JS 代码');";
[jsContext evaluateScript:jsCode];

// 3. 方式2：调用 JS 中定义的方法
// JS 层提前定义全局方法：window.nativeCallback = (data) => { ... }
JSValue *nativeCallback = jsContext[@"nativeCallback"];
if ([nativeCallback isFunction]) {
// 传递参数（原生 → JS）
NSDictionary *data = @{@"type": @"network", @"status": @"online"};
[nativeCallback callWithArguments:@[data]];
}
JS 层接收原生调用

// 定义全局方法，供原生调用
window.nativeCallback = (data) => {
console.log('原生传递的参数：', data);
// 根据参数执行逻辑（如更新网络状态UI）
if (data.type === 'network') {
this.networkStatus = data.status;
}
};

四、通信的进阶能力：事件监听与双向绑定

事件监听（Native → JS）

Weex 支持原生向 JS 发送事件，JS 通过 $on 监听：

复制代码

// iOS 原生发送事件
[self.weexInstance fireGlobalEvent:@"networkChange" params:@{@"status": @"offline"}];

// JS 监听事件
this.$on('networkChange', (params) => {
  console.log('网络状态变化：', params.status);
});

双向通信注意事项

线程安全 ：原生调用 JS 需在主线程执行（iOS 的 JSContext 非线程安全）；
参数校验：JS 传递的参数需在原生层校验（避免空值、类型错误）；
内存泄漏：原生持有 JS 回调时，需在页面销毁时释放，避免循环引用；
性能优化：减少频繁通信（如批量传递参数），避免 JSBridge 成为性能瓶颈。

五、面试加分点与记忆法

加分点

区分同步/异步通信：Weex 内置模块多数为异步，自定义模块可通过 WXSyncMethod 实现同步调用；
跨端一致性：自定义模块需同时实现 iOS/Android 版本，保证 JS 调用的跨端统一；
错误处理：原生模块需捕获异常，通过回调返回错误信息，避免 JS 层崩溃。

记忆法

核心流程记忆法："JS 调原生：导入模块 → 调用方法 → 原生解析 → 执行逻辑 → 回调 JS；原生调 JS：获取上下文 → 执行代码/调用方法 → JS 接收参数 → 执行逻辑"；
核心载体记忆法："JSBridge 是桥梁，iOS 用 JSC，Android 用 V8/JSC，参数传 JSON，回调靠闭包"。

请说明 Weex 的渲染原理

Weex 的核心优势是"一套代码，原生渲染"，其渲染原理区别于 WebView 的 DOM 渲染和 React Native 的虚拟 DOM 映射，核心是"JS 层生成虚拟 DOM → 桥接层通信 → 原生层创建原生组件 → 布局渲染"，完整流程分为"编译阶段、运行时阶段、渲染阶段"，以下详细拆解：

一、渲染前置：Weex 代码的编译阶段

Weex 前端代码以 .vue 文件（模板+样式+脚本）编写，编译阶段将其转换为 JS 包（bundle.js），供运行时解析：

复制代码

<!-- 示例 .vue 文件 -->
<template>
  <div class="container">
    <image :src="imageUrl" class="logo"></image>
    <text class="title" @click="onClick">{{ title }}</text>
  </div>
</template>
<style scoped>
.container { flex: 1; justify-content: center; align-items: center; }
.logo { width: 100px; height: 100px; }
.title { font-size: 32px; color: #333; margin-top: 20px; }
</style>
<script>
export default {
  data() {
    return {
      title: 'Weex 渲染示例',
      imageUrl: 'https://xxx/logo.png'
    };
  },
  methods: {
    onClick() {
      console.log('点击文字');
    }
  }
};
</script>

编译流程：

模板解析 ：将 <template> 解析为 AST（抽象语法树），分析节点类型（如 div、image、text）、属性、样式、事件；
样式处理 ：将 CSS 样式转换为 JS 对象，基于 Flexbox 布局规则标准化（如 justify-content 转换为 justifyContent）；
脚本编译：将 ES6+ 脚本编译为 ES5，绑定数据和方法；
打包生成 ：将 AST、样式、脚本打包为 bundle.js，包含虚拟 DOM 生成逻辑和业务逻辑。

二、核心阶段1：运行时生成虚拟 DOM（JS 层）

Weex 运行时（JS Framework）加载 bundle.js 后，执行以下逻辑生成虚拟 DOM（VNode）：

数据绑定 ：将 data 中的数据（如 title、imageUrl）绑定到模板节点；

VNode 构建 ：将 AST 转换为 VNode（JS 对象），描述 UI 结构，示例：

复制代码

{
  tag: 'div',
  attrs: { class: 'container' },
  style: { flex: 1, justifyContent: 'center', alignItems: 'center' },
  children: [
    {
      tag: 'image',
      attrs: { src: 'https://xxx/logo.png' },
      style: { width: 100, height: 100 },
      type: 'image'
    },
    {
      tag: 'text',
      attrs: { class: 'title' },
      style: { fontSize: 32, color: '#333', marginTop: 20 },
      events: { click: 'onClick' },
      text: 'Weex 渲染示例',
      type: 'text'
    }
  ],
  type: 'div'
}

VNode 标准化 ：统一跨端的节点类型和样式属性（如 iOS/Android 对 px 的适配）。

三、核心阶段2：桥接层通信（JS → 原生）

JS 层将 VNode 序列化为 JSON 字符串，通过 JSBridge 传递给原生层，核心流程：

序列化 ：将 VNode 转换为 JSON（如 {"tag":"div","style":{"flex":1},"children":[]}）；
通信传递 ：
- iOS 端：通过 ScriptCore 的 JSContext 将 JSON 传递给 OC 代码；
- Android 端：通过 V8/JSC 将 JSON 传递给代码；
指令分发：原生层接收 JSON 后，解析为"创建节点、设置样式、绑定事件"等指令。

四、核心阶段3：原生层渲染（iOS/Android）

原生层接收指令后，创建对应的原生组件并完成布局渲染，以 iOS 为例：

组件映射（Weex 节点 → iOS 原生组件）

Weex 定义了标准化的节点与原生组件的映射关系，保证跨端一致性：

Weex 节点	iOS 原生组件	Android 原生组件	说明
div	UIView	ViewGroup	容器组件，用于布局
text	UILabel	TextView	文本组件
image	UIImageView	ImageView	图片组件
list	UITableView	RecyclerView	列表组件
scroller	UIScrollView	ScrollView	滚动组件
input	UITextField	EditText	输入组件

渲染流程（iOS 端）

// 1. 解析 JSON 指令，创建对应组件
- (void)createComponentWithJSON:(NSString *)json {
  NSDictionary *vnode = [NSJSONSerialization JSONObjectWithData:[json dataUsingEncoding:NSUTF8StringEncoding] options:0 error:nil];
  NSString *tag = vnode[@"tag"];
  NSDictionary *style = vnode[@"style"];
  
  // 2. 根据 tag 创建原生组件
  UIView *component = nil;
  if ([tag isEqualToString:@"div"]) {
  component = [[UIView alloc] init];
  } else if ([tag isEqualToString:@"text"]) {
  component = [[UILabel alloc] init];
  ((UILabel *)component).text = vnode[@"text"];
  } else if ([tag isEqualToString:@"image"]) {
  component = [[UIImageView alloc] init];
  NSString *imageUrl = vnode[@"attrs"][@"src"];
  // 异步加载图片
  [((UIImageView *)component) sd_setImageWithURL:[NSURL URLWithString:imageUrl]];
  }
  
  // 3. 设置样式（基于 Flexbox 布局）
  [self applyStyle:style toComponent:component];
  
  // 4. 添加到父容器，构建视图层级
  UIView *parentComponent = [self getParentComponentWithId:vnode[@"parentId"]];
  [parentComponent addSubview:component];
  
  // 5. 绑定事件（如点击）
  [self bindEvents:vnode[@"events"] toComponent:component];
  }
// 6. Flexbox 布局计算
- (void)applyStyle:(NSDictionary *)style toComponent:(UIView *)component {
  // Weex 内置 Flexbox 布局引擎（Yoga），计算组件的 frame
  YogaNode *yogaNode = [YogaNode new];
  [yogaNode setFlex:[[style objectForKey:@"flex"] floatValue]];
  [yogaNode setJustifyContent:YogaJustifyCenter];
  [yogaNode calculateLayoutWithSize:CGSizeMake(parentComponent.bounds.size.width, parentComponent.bounds.size.height)];
  component.frame = CGRectMake(yogaNode.layoutLeft, yogaNode.layoutTop, yogaNode.layoutWidth, yogaNode.layoutHeight);
  }
关键技术：Yoga 布局引擎

Weex 采用 Facebook 开源的 Yoga 布局引擎（C++ 实现），统一跨端的 Flexbox 布局计算：

原生层通过 Yoga 解析 VNode 中的样式属性，计算组件的 frame（位置和大小）；
保证 iOS/Android/H5 端的布局结果完全一致，解决跨端布局适配问题。

五、渲染优化：增量更新与预渲染

增量更新

当 JS 层数据变化（如 title 改变），Weex 不会重新生成完整 VNode，而是仅更新变化的节点（增量 VNode），原生层仅更新对应组件的属性，避免全量渲染，提升性能。

预渲染

提前加载常用页面的 bundle.js，预生成 VNode；
原生层预创建高频使用的组件（如 list 的 cell），减少渲染时的创建耗时。

六、面试加分点与记忆法

加分点

区分 Weex 与 React Native 渲染差异：Weex 直接将 VNode 转换为原生组件，RN 通过虚拟 DOM 映射原生组件，Weex 渲染更接近原生；
渲染性能优化：增量更新、Yoga 布局预计算、图片懒加载；
跨端一致性：Yoga 引擎保证布局一致，组件映射保证视觉一致。

记忆法

核心流程记忆法："编译成 JS 包 → 运行时生成 VNode → JSBridge 传 JSON → 原生解析指令 → Yoga 算布局 → 创建原生组件 → 渲染UI"；
核心技术记忆法："VNode 描述结构，Yoga 计算布局，JSBridge 做通信，原生组件来渲染"。

给定一个数组，其中一个数字出现奇数次，其余数字均出现偶数次，要求不开辟额外内存空间，如何找到这个数字？（完整实现）

一、核心思路：利用异或运算的特性

异或运算（^）是解决该问题的关键，其核心特性如下：

自反性 ：任何数与自身异或结果为 0（a ^ a = 0）；
恒等性 ：任何数与 0 异或结果为自身（a ^ 0 = a）；
交换律/结合律 ：a ^ b ^ c = a ^ c ^ b = (a ^ b) ^ c。

基于以上特性，将数组中所有数字依次异或：

出现偶数次的数字会两两异或为 0（如 a ^ a = 0）；
最终结果为出现奇数次的数字（0 ^ 目标数字 = 目标数字）。

该方案时间复杂度为 O(n)（仅遍历数组一次），空间复杂度为 O(1)（仅使用一个临时变量），完全满足"不开辟额外内存空间"的要求。

二、Swift 完整实现

复制代码

/// 找到数组中出现奇数次的数字（其余数字出现偶数次）
/// - Parameter nums: 输入数组（非空，且保证有且仅有一个数字出现奇数次）
/// - Returns: 出现奇数次的数字
func findOddOccurrenceNumber(in nums: [Int]) -> Int {
    // 初始化结果为 0（恒等性：0 ^ a = a）
    var result = 0
    // 遍历数组，依次异或
    for num in nums {
        result ^= num
    }
    return result
}

// 测试案例
func testFindOddOccurrenceNumber() {
    // 测试用例1：基础场景（1出现1次，其余出现2次）
    let case1 = [1, 2, 2, 3, 3, 4, 4]
    assert(findOddOccurrenceNumber(in: case1) == 1, "测试用例1失败")
    
    // 测试用例2：目标数字出现在末尾（5出现3次，其余出现2次）
    let case2 = [6, 6, 7, 7, 5, 5, 5]
    assert(findOddOccurrenceNumber(in: case2) == 5, "测试用例2失败")
    
    // 测试用例3：单元素数组（唯一元素出现1次）
    let case3 = [8]
    assert(findOddOccurrenceNumber(in: case3) == 8, "测试用例3失败")
    
    // 测试用例4：负数场景（-2出现3次，其余出现2次）
    let case4 = [-1, -1, -2, -2, -2, 3, 3]
    assert(findOddOccurrenceNumber(in: case4) == -2, "测试用例4失败")
    
    print("所有测试用例通过！")
}

// 执行测试
testFindOddOccurrenceNumber()

三、逻辑验证（以测试用例1为例）

数组 [1, 2, 2, 3, 3, 4, 4] 的异或过程：

复制代码

result = 0
0 ^ 1 = 1
1 ^ 2 = 3
3 ^ 2 = 1
1 ^ 3 = 2
2 ^ 3 = 1
1 ^ 4 = 5
5 ^ 4 = 1
最终 result = 1（正确）

四、边界场景处理

单元素数组 ：数组仅有一个元素时，该元素即为目标数字（0 ^ 元素 = 元素）；
负数场景：异或运算对负数同样生效（二进制补码运算），无需额外处理；
目标数字出现多次奇数次 ：如出现3次、5次等，异或结果仍为该数字（a ^ a ^ a = a）。

五、面试加分点与记忆法

加分点

时间/空间复杂度分析：时间 O(n)，空间 O(1)，最优解；
异或运算的底层原理：基于二进制位运算，相同位为0，不同位为1，解释自反性/恒等性的底层逻辑；
扩展思考：若题目改为"多个数字出现奇数次"，该方法不适用，需结合哈希表（但会占用额外空间）。

记忆法

核心逻辑记忆法："偶数次异或为0，奇数次异或留自身，遍历异或找目标"；
异或特性记忆法："自反（a^a=0）、恒等（a^0=a），遍历异或解问题"。

给定一个数组，其中两个数字各出现一次，其余数字均出现两次，要求不开辟额外内存空间，如何找到这两个数字？（完整实现）

一、核心思路：分治 + 异或运算

该问题是"单数字奇数次"的扩展，核心仍基于异或运算，需分两步解决：

第一步：整体异或，得到两个目标数字的异或结果 数组中所有数字异或后，结果为 a ^ b（a、b 为仅出现一次的数字，其余数字异或为0）。
第二步：拆分数组，分别异或找到 a 和 b
- 找到 a ^ b 的二进制中任意一个为1的位（记为第 k 位），该位表示 a 和 b 在该位上的二进制值不同（一个为0，一个为1）；
- 根据第 k 位是否为1，将数组拆分为两个子数组：
  - 子数组1：第 k 位为1的数字（包含 a 或 b）；
  - 子数组2：第 k 位为0的数字（包含另一个数字）；
- 对两个子数组分别异或，得到 a 和 b。

该方案时间复杂度 O(n)（两次遍历数组），空间复杂度 O(1)，满足"不开辟额外内存空间"的要求。

二、Swift 完整实现

复制代码

/// 找到数组中仅出现一次的两个数字（其余数字出现两次）
/// - Parameter nums: 输入数组（非空，且保证有且仅有两个数字出现一次）
/// - Returns: 两个仅出现一次的数字（元组形式）
func findTwoUniqueNumbers(in nums: [Int]) -> (Int, Int) {
    // 步骤1：整体异或，得到 a ^ b 的结果
    var xorResult = 0
    for num in nums {
        xorResult ^= num
    }
    
    // 步骤2：找到 xorResult 中第一个为1的二进制位（用于拆分数组）
    // 技巧：利用 n & (-n) 找到最低位的1（补码特性）
    let mask = xorResult & (-xorResult)
    
    // 步骤3：根据 mask 拆分数组，分别异或
    var a = 0, b = 0
    for num in nums {
        if (num & mask) == 0 {
            // 第 k 位为0的数字，异或得到 a
            a ^= num
        } else {
            // 第 k 位为1的数字，异或得到 b
            b ^= num
        }
    }
    
    return (a, b)
}

// 测试案例
func testFindTwoUniqueNumbers() {
    // 测试用例1：基础场景（1、2出现一次，其余出现两次）
    let case1 = [1, 2, 3, 3, 4, 4]
    let result1 = findTwoUniqueNumbers(in: case1)
    assert((result1.0 == 1 && result1.1 == 2) || (result1.0 == 2 && result1.1 == 1), "测试用例1失败")
    
    // 测试用例2：包含负数（-1、5出现一次，其余出现两次）
    let case2 = [-1, 5, 2, 2, -3, -3]
    let result2 = findTwoUniqueNumbers(in: case2)
    assert((result2.0 == -1 && result2.1 == 5) || (result2.0 == 5 && result2.1 == -1), "测试用例2失败")
    
    // 测试用例3：大数场景（100、200出现一次，其余出现两次）
    let case3 = [100, 200, 99, 99, 88, 88]
    let result3 = findTwoUniqueNumbers(in: case3)
    assert((result3.0 == 100 && result3.1 == 200) || (result3.0 == 200 && result3.1 == 100), "测试用例3失败")
    
    // 测试用例4：两个数字二进制位差异在高位（8=1000，16=10000）
    let case4 = [8, 16, 4, 4, 2, 2]
    let result4 = findTwoUniqueNumbers(in: case4)
    assert((result4.0 == 8 && result4.1 == 16) || (result4.0 == 16 && result4.1 == 8), "测试用例4失败")
    
    print("所有测试用例通过！")
}

// 执行测试
testFindTwoUniqueNumbers()

三、逻辑验证（以测试用例1为例）

数组 [1, 2, 3, 3, 4, 4] 的处理过程：

整体异或 ：1 ^ 2 ^ 3 ^ 3 ^ 4 ^ 4 = 1 ^ 2 = 3（二进制 11）；
找最低位的1 ：3 & (-3) = 1（二进制 01，最低位第0位为1）；
拆分数组 ：
- 第0位为0的数字：2（二进制 10）、4、4 → 异或结果：2 ^ 4 ^ 4 = 2；
- 第0位为1的数字：1（二进制 01）、3、3 → 异或结果：1 ^ 3 ^ 3 = 1；
最终结果：(1, 2) 或 (2, 1)（正确）。

四、关键技巧解析

n & (-n) 找最低位的1 ：基于二进制补码特性，-n 是 n 的反码加1，n & (-n) 会保留 n 中最低位的1，其余位为0。例如：
- 3（00000011）的补码是 11111101，3 & (-3) = 1（00000001）；
- 8（00001000）的补码是 11111000，8 & (-8) = 8（00001000）。
拆分数组的合理性 ：a ^ b 的二进制位为1的位置，表示 a 和 b 在该位上的值不同，因此拆分后的两个子数组必然分别包含 a 和 b，且其余数字成对出现在同一子数组中（异或后为0）。

五、面试加分点与记忆法

加分点

分治思想的应用：将"找两个数字"的问题拆分为"找一个数字"的子问题；
二进制位运算的深度理解：解释 n & (-n) 的底层原理（补码）；
结果顺序：说明返回结果的顺序不固定，可根据业务需求排序；
扩展思考：若题目改为"多个数字出现一次"，需结合哈希表（但占用额外空间）。

记忆法

核心流程记忆法："整体异或得a^b，找1位拆数组，子数组异或找a和b"；
技巧记忆法："n&(-n)找最低1，拆分数组分治解"。

如何判断一个链表是否存在环？若存在环，如何找到环的入口节点？（完整实现）

一、核心思路

判断链表是否有环：快慢指针法（Floyd 龟兔赛跑算法）

定义两个指针：慢指针（slow）每次走1步，快指针（fast）每次走2步；
若链表无环，快指针会先到达链表尾部（nil）；
若链表有环，快指针会追上慢指针（二者指向同一节点）。

找环的入口节点：快慢指针+数学推导

设链表结构：头节点 → 入口节点（距离 x）→ 相遇节点（距离 y）→ 入口节点（距离 z），环的长度为 y + z。

相遇时，慢指针走了 x + y 步，快指针走了 x + y + n(y + z) 步（n 为快指针绕环的圈数）；
由于快指针速度是慢指针的2倍：2(x + y) = x + y + n(y + z) → x = n(y + z) - y = (n-1)(y + z) + z；
结论：相遇后，将慢指针重置为头节点，快慢指针均每次走1步，再次相遇时即为环的入口节点。

二、Swift 完整实现

链表节点定义

/// 链表节点
class ListNode {
var val: Int
var next: ListNode?
init(_ val: Int) {
self.val = val
self.next = nil
}
}
判断链表是否有环

/// 判断链表是否存在环
/// - Parameter head: 链表头节点
/// - Returns: (是否有环, 快慢指针相遇节点)
func hasCycle(_ head: ListNode?) -> (Bool, ListNode?) {
guard let head = head else {
return (false, nil)
}
var slow: ListNode? = head
var fast: ListNode? = head
复制代码
```
 while fast != nil && fast?.next != nil {
     slow = slow?.next // 慢指针走1步
     fast = fast?.next?.next // 快指针走2步
     
     if slow === fast {
         // 相遇，存在环
         return (true, slow)
     }
 }
 // 快指针到达尾部，无环
 return (false, nil)
```
}
找到环的入口节点

/// 找到链表环的入口节点（若存在环）
/// - Parameter head: 链表头节点
/// - Returns: 环的入口节点（无环则返回nil）
func findCycleEntrance(_ head: ListNode?) -> ListNode? {
let (hasCycle, meetNode) = hasCycle(head)
guard hasCycle, let meetNode = meetNode else {
return nil
}
复制代码
```
 // 慢指针重置为头节点，快慢指针均走1步
 var slow: ListNode? = head
 var fast: ListNode? = meetNode
 
 while slow !== fast {
     slow = slow?.next
     fast = fast?.next
 }
 
 // 再次相遇，即为入口节点
 return slow
```
}

测试案例

// 构建带环链表：1 → 2 → 3 → 4 → 2（环的入口为2）
func buildCycleList() -> ListNode {
let node1 = ListNode(1)
let node2 = ListNode(2)
let node3 = ListNode(3)
let node4 = ListNode(4)
node1.next = node2
node2.next = node3
node3.next = node4
node4.next = node2 // 构建环
return node1
}

// 构建无环链表：1 → 2 → 3 → 4
func buildNormalList() -> ListNode {
let node1 = ListNode(1)
let node2 = ListNode(2)
let node3 = ListNode(3)
let node4 = ListNode(4)
node1.next = node2
node2.next = node3
node3.next = node4
return node1
}

// 测试函数
func testLinkedListCycle() {
// 测试1：带环链表判断
let cycleList = buildCycleList()
let (hasCycle1, _) = hasCycle(cycleList)
assert(hasCycle1 == true, "测试1失败：带环链表判断错误")

复制代码

 // 测试2：无环链表判断
 let normalList = buildNormalList()
 let (hasCycle2, _) = hasCycle(normalList)
 assert(hasCycle2 == false, "测试2失败：无环链表判断错误")
 
 // 测试3：找环的入口节点
 let entrance = findCycleEntrance(cycleList)
 assert(entrance?.val == 2, "测试3失败：环的入口节点错误")
 
 // 测试4：空链表
 let (hasCycle4, _) = hasCycle(nil)
 assert(hasCycle4 == false, "测试4失败：空链表判断错误")
 
 // 测试5：单节点无环
 let singleNode = ListNode(5)
 let (hasCycle5, _) = hasCycle(singleNode)
 assert(hasCycle5 == false, "测试5失败：单节点无环判断错误")
 
 // 测试6：单节点有环（自环）
 let selfCycleNode = ListNode(6)
 selfCycleNode.next = selfCycleNode
 let (hasCycle6, _) = hasCycle(selfCycleNode)
 let entrance6 = findCycleEntrance(selfCycleNode)
 assert(hasCycle6 == true && entrance6?.val == 6, "测试6失败：单节点自环判断错误")
 
 print("所有测试用例通过！")

}

// 执行测试
testLinkedListCycle()

三、逻辑验证（带环链表示例）

链表结构：1 → 2 → 3 → 4 → 2（入口为2）：

判断环：
- 慢指针：1 → 2 → 3 → 4 → 2；
- 快指针：1 → 3 → 2 → 4 → 2；
- 快慢指针在节点2相遇，判断存在环。
找入口：
- 慢指针重置为1，快指针在2；
- 慢指针：1 → 2；
- 快指针：2 → 3 → 4 → 2；
- 二者在节点2相遇，即为入口（正确）。

四、复杂度分析

时间复杂度 ：
- 判断环：O(n)，最坏情况下遍历链表所有节点；
- 找入口：O(n)，重置后遍历链表至入口节点；
- 整体：O(n)。
空间复杂度：O(1)，仅使用两个指针，无额外内存空间。

五、面试加分点与记忆法

加分点

算法优化：对比哈希表法（空间O(n)），快慢指针法空间更优；
数学推导：清晰解释 x = (n-1)(y+z) + z 的推导过程；
边界场景：单节点自环、空链表、无环链表的处理；
扩展思考：若需计算环的长度，可在相遇后让快指针继续走，再次相遇时统计步数。

记忆法

判断环记忆法："快慢指针，慢1快2，相遇有环，快到尾无环"；
找入口记忆法："相遇重置慢指针，快慢同速走，相遇即入口"。

请实现 "旋转数组找最小数字" 的算法。（完整实现）

一、问题背景与核心思路

旋转数组指将一个有序递增数组（如 [1,2,3,4,5]）的前若干个元素移到数组末尾形成的数组（如旋转2次得到 [3,4,5,1,2]）。找最小数字的核心目标是在 O(log n) 时间复杂度内找到最小值，而非暴力遍历（O(n)），核心思路是二分查找，利用旋转数组的"部分有序"特性缩小查找范围：

旋转数组分为左右两个有序子数组，左子数组所有元素 ≥ 右子数组所有元素，最小值是右子数组的第一个元素；
二分查找中，比较中间元素 nums[mid] 与右边界元素 nums[right]：
- 若 nums[mid] < nums[right]：最小值在左半区（mid 或左侧），调整右边界为 mid；
- 若 nums[mid] > nums[right]：最小值在右半区（mid 右侧），调整左边界为 mid + 1；
- 若 nums[mid] == nums[right]：无法判断，右边界左移一位（处理重复元素）；
最终 left == right 时，该位置即为最小值。

二、Swift 完整实现

复制代码

/// 旋转数组找最小数字（支持重复元素）
/// - Parameter nums: 旋转后的有序递增数组（非空）
/// - Returns: 数组中的最小值
func findMinInRotatedArray(_ nums: [Int]) -> Int {
    guard !nums.isEmpty else {
        fatalError("数组不能为空")
    }
    
    var left = 0
    var right = nums.count - 1
    
    while left < right {
        let mid = left + (right - left) / 2 // 避免整数溢出
        
        if nums[mid] < nums[right] {
            // 最小值在左半区（包含mid）
            right = mid
        } else if nums[mid] > nums[right] {
            // 最小值在右半区（mid右侧）
            left = mid + 1
        } else {
            // 处理重复元素，右边界左移
            right -= 1
        }
    }
    
    return nums[left]
}

// 测试案例
func testFindMinInRotatedArray() {
    // 测试用例1：无重复元素，正常旋转
    let case1 = [3,4,5,1,2]
    assert(findMinInRotatedArray(case1) == 1, "测试用例1失败")
    
    // 测试用例2：无重复元素，未旋转（原数组有序）
    let case2 = [1,2,3,4,5]
    assert(findMinInRotatedArray(case2) == 1, "测试用例2失败")
    
    // 测试用例3：包含重复元素
    let case3 = [2,2,2,0,1]
    assert(findMinInRotatedArray(case3) == 0, "测试用例3失败")
    
    // 测试用例4：全重复元素
    let case4 = [5,5,5,5]
    assert(findMinInRotatedArray(case4) == 5, "测试用例4失败")
    
    // 测试用例5：单元素数组
    let case5 = [7]
    assert(findMinInRotatedArray(case5) == 7, "测试用例5失败")
    
    // 测试用例6：旋转后最小值在中间
    let case6 = [4,5,6,7,0,1,2]
    assert(findMinInRotatedArray(case6) == 0, "测试用例6失败")
    
    print("所有测试用例通过！")
}

// 执行测试
testFindMinInRotatedArray()

三、逻辑验证（以测试用例1为例）

数组 [3,4,5,1,2] 的查找过程：

left=0, right=4, mid=2 → nums[mid]=5 > nums[right]=2 → left=3；
left=3, right=4, mid=3 → nums[mid]=1 < nums[right]=2 → right=3；
left=3, right=3 → 循环结束，返回 nums[3]=1（正确）。

四、关键细节与边界处理

避免整数溢出 ：mid = left + (right - left) / 2 替代 (left + right) / 2，防止 left + right 超出Int范围；
重复元素处理 ：当 nums[mid] == nums[right] 时，无法判断最小值位置，右边界左移（如 [2,2,0,2]）；
未旋转数组：二分查找会逐步将右边界移至0，最终返回第一个元素（正确）。

五、面试加分点与记忆法

加分点

时间复杂度分析：无重复元素时 O(log n)，有重复元素时最坏 O(n)（如全重复）；
算法优化：对比暴力遍历（O(n)），二分查找效率更高；
扩展思考：若数组是递减旋转，调整比较逻辑（对比 nums[mid] 与左边界）。

记忆法

核心逻辑记忆法："二分找mid，比右边界，小则左缩，大则右缩，相等右移，最终left是最小"；
边界记忆法："空数组报错，单元素直接返，重复元素右边界左移"。

请实现 "查找某路径是否存在于某二叉树内" 的算法。（完整实现）

一、问题背景与核心思路

二叉树路径查找指判断从根节点到叶子节点的路径中，是否存在一条路径的节点值序列与目标路径完全匹配（如二叉树路径 1→2→3 匹配目标路径 [1,2,3]）。核心思路是深度优先搜索（DFS）（递归实现）：

递归终止条件：
- 若当前节点为 nil，且目标路径已遍历完 → 不匹配；
- 若当前节点为 nil，目标路径未遍历完 → 不匹配；
- 若当前节点值 ≠ 目标路径当前值 → 不匹配；
- 若当前节点是叶子节点，且目标路径遍历到最后一位 → 匹配；
递归过程：
- 检查当前节点值是否等于目标路径的当前索引值；
- 递归查找左子树和右子树，只要有一个子树匹配则返回 true。

二、Swift 完整实现

复制代码

/// 二叉树节点定义
class TreeNode {
    var val: Int
    var left: TreeNode?
    var right: TreeNode?
    init(_ val: Int) {
        self.val = val
        self.left = nil
        self.right = nil
    }
}

/// 查找二叉树中是否存在目标路径（根到叶子）
/// - Parameters:
///   - root: 二叉树根节点
///   - path: 目标路径数组
/// - Returns: 是否存在匹配路径
func hasPath(_ root: TreeNode?, _ path: [Int]) -> Bool {
    // 辅助递归函数
    func dfs(_ node: TreeNode?, _ path: [Int], _ index: Int) -> Bool {
        // 终止条件1：节点为空
        guard let node = node else {
            return index == path.count // 路径遍历完才匹配（空树匹配空路径）
        }
        
        // 终止条件2：当前节点值不匹配
        if index >= path.count || node.val != path[index] {
            return false
        }
        
        // 终止条件3：当前节点是叶子节点，且路径遍历完
        if node.left == nil && node.right == nil && index == path.count - 1 {
            return true
        }
        
        // 递归查找左、右子树
        let leftMatch = dfs(node.left, path, index + 1)
        let rightMatch = dfs(node.right, path, index + 1)
        
        return leftMatch || rightMatch
    }
    
    // 空路径特殊处理：只有空树匹配
    if path.isEmpty {
        return root == nil
    }
    
    return dfs(root, path, 0)
}

// 构建测试二叉树：
//        1
//       / \
//      2   3
//     / \   \
//    4   5   6
func buildTestTree() -> TreeNode {
    let root = TreeNode(1)
    let node2 = TreeNode(2)
    let node3 = TreeNode(3)
    let node4 = TreeNode(4)
    let node5 = TreeNode(5)
    let node6 = TreeNode(6)
    
    root.left = node2
    root.right = node3
    node2.left = node4
    node2.right = node5
    node3.right = node6
    
    return root
}

// 测试案例
func testHasPath() {
    let root = buildTestTree()
    
    // 测试用例1：存在匹配路径（1→2→4）
    let case1 = [1,2,4]
    assert(hasPath(root, case1) == true, "测试用例1失败")
    
    // 测试用例2：存在匹配路径（1→3→6）
    let case2 = [1,3,6]
    assert(hasPath(root, case2) == true, "测试用例2失败")
    
    // 测试用例3：路径长度不匹配（1→2）
    let case3 = [1,2]
    assert(hasPath(root, case3) == false, "测试用例3失败")
    
    // 测试用例4：路径值不匹配（1→2→7）
    let case4 = [1,2,7]
    assert(hasPath(root, case4) == false, "测试用例4失败")
    
    // 测试用例5：空路径（空树匹配，非空树不匹配）
    let case5: [Int] = []
    assert(hasPath(root, case5) == false, "测试用例5失败")
    assert(hasPath(nil, case5) == true, "测试用例5-2失败")
    
    // 测试用例6：单节点树匹配
    let singleNode = TreeNode(5)
    assert(hasPath(singleNode, [5]) == true, "测试用例6失败")
    
    // 测试用例7：单节点树不匹配
    assert(hasPath(singleNode, [6]) == false, "测试用例7失败")
    
    print("所有测试用例通过！")
}

// 执行测试
testHasPath()

三、逻辑验证（以测试用例1为例）

目标路径 [1,2,4] 的查找过程：

根节点1（index=0）→ 值匹配，递归左子树2（index=1）；
节点2（index=1）→ 值匹配，递归左子树4（index=2）；
节点4（index=2）→ 值匹配，且是叶子节点，index=2等于路径长度-1 → 返回true。

四、关键细节与边界处理

空路径处理：只有空树匹配空路径，非空树不匹配；
叶子节点判断 ：必须是根到叶子的路径，中间节点匹配不算（如 [1,2] 不匹配）；
索引越界处理：index ≥ path.count 直接返回false，避免数组越界。

五、面试加分点与记忆法

加分点

算法扩展：可改为迭代实现（栈模拟DFS），避免递归栈溢出；
时间/空间复杂度：时间 O(n)（遍历所有节点），空间 O(h)（h为树高，递归栈深度）；
扩展思考：若路径不要求到叶子节点，修改终止条件（去掉叶子节点判断）。

记忆法

核心逻辑记忆法："递归DFS，逐位匹配，节点空判长度，值不等返回false，叶子且到尾返回true，左右子树有一个匹配即成功"；
边界记忆法："空路径配空树，非空树不配，叶子节点才收尾"。

请实现 "翻转字符串" 的算法。（完整实现）

一、问题背景与核心思路

翻转字符串指将字符串的字符顺序完全反转（如 "hello" → "olleh"），核心要求是原地翻转 （空间 O(1)），Swift 中 String 是值类型且不可变，需转换为可变的 Array<Character> 操作：

双指针法：定义左指针（left）从0开始，右指针（right）从字符串末尾开始；
交换左右指针指向的字符，左指针右移，右指针左移；
直到 left ≥ right 时停止，将数组转回字符串。

二、Swift 完整实现

复制代码

/// 原地翻转字符串（空间O(1)）
/// - Parameter str: 输入字符串（会被修改）
/// - Returns: 翻转后的字符串
func reverseString(_ str: inout String) -> String {
    guard !str.isEmpty else {
        return str
    }
    
    // 转换为可变字符数组
    var chars = Array(str)
    var left = 0
    var right = chars.count - 1
    
    while left < right {
        // 交换左右指针字符
        chars.swapAt(left, right)
        // 移动指针
        left += 1
        right -= 1
    }
    
    // 转回字符串并更新原字符串
    str = String(chars)
    return str
}

/// 扩展：翻转字符串中的单词（如 "hello world" → "world hello"）
func reverseWords(in str: inout String) -> String {
    // 先翻转整个字符串
    _ = reverseString(&str)
    // 按空格分割为单词数组
    var words = str.components(separatedBy: .whitespaces).filter { !$0.isEmpty }
    // 翻转每个单词
    for i in 0..<words.count {
        var word = words[i]
        _ = reverseString(&word)
        words[i] = word
    }
    // 拼接为字符串
    str = words.joined(separator: " ")
    return str
}

// 测试案例
func testReverseString() {
    // 测试用例1：普通字符串
    var case1 = "hello"
    assert(reverseString(&case1) == "olleh", "测试用例1失败")
    
    // 测试用例2：空字符串
    var case2 = ""
    assert(reverseString(&case2) == "", "测试用例2失败")
    
    // 测试用例3：单字符字符串
    var case3 = "a"
    assert(reverseString(&case3) == "a", "测试用例3失败")
    
    // 测试用例4：包含空格的字符串
    var case4 = "hello world"
    assert(reverseString(&case4) == "dlrow olleh", "测试用例4失败")
    
    // 测试用例5：包含特殊字符的字符串
    var case5 = "123@abc"
    assert(reverseString(&case5) == "cba@321", "测试用例5失败")
    
    // 扩展测试：翻转单词
    var case6 = "hello world"
    assert(reverseWords(in: &case6) == "world hello", "测试用例6失败")
    
    // 扩展测试：多个空格
    var case7 = "  a b c  "
    assert(reverseWords(in: &case7) == "c b a", "测试用例7失败")
    
    print("所有测试用例通过！")
}

// 执行测试
testReverseString()

三、逻辑验证（以测试用例1为例）

字符串 "hello" 转换为数组 ["h","e","l","l","o"]：

left=0, right=4 → 交换 h 和 o → ["o","e","l","l","h"]；
left=1, right=3 → 交换 e 和 l → ["o","l","l","e","h"]；
left=2, right=2 → 循环结束，转回字符串 "olleh"（正确）。

四、关键细节与边界处理

inout 参数 ：Swift 中 String 不可变，需用 inout 修饰实现原地修改；
空字符串/单字符：直接返回原字符串，避免指针越界；
特殊字符/空格：双指针法对所有字符类型生效，无需额外处理。

五、面试加分点与记忆法

加分点

算法优化：对比递归翻转（空间 O(n)），双指针法空间 O(1) 更优；
扩展功能：实现单词翻转，体现对字符串处理的深度理解；
编码规范：参数校验（空字符串），避免运行时错误。

记忆法

核心逻辑记忆法："转数组，双指针，左0右尾，交换字符，指针相向移，直到相遇"；
扩展记忆法："先翻整体，再翻单词，过滤空格，拼接结果"。

请实现 "翻转单链表" 的算法。（完整实现）

一、问题背景与核心思路

翻转单链表指将链表的节点指向完全反转（如 1→2→3→nil → 3→2→1→nil），核心思路有两种：

迭代法（推荐） ：双指针+临时指针，原地翻转（空间 O(1)）：
- 定义 prev（前一个节点，初始 nil）、curr（当前节点，初始根节点）；
- 每次保存 curr.next 到临时变量 temp；
- 将 curr.next 指向 prev，然后 prev 移到 curr，curr 移到 temp；
- 循环至 curr 为 nil，prev 即为新头节点。
递归法：递归到链表尾部，从后往前翻转（空间 O(n)，递归栈深度）。

二、Swift 完整实现

复制代码

/// 单链表节点定义
class ListNode {
    var val: Int
    var next: ListNode?
    init(_ val: Int) {
        self.val = val
        self.next = nil
    }
}

/// 迭代法翻转单链表（空间O(1)）
/// - Parameter head: 链表头节点
/// - Returns: 翻转后的头节点
func reverseListIterative(_ head: ListNode?) -> ListNode? {
    var prev: ListNode? = nil
    var curr = head
    
    while curr != nil {
        // 保存当前节点的下一个节点
        let temp = curr?.next
        // 翻转当前节点的指向
        curr?.next = prev
        // 移动指针
        prev = curr
        curr = temp
    }
    
    // prev 是新的头节点
    return prev
}

/// 递归法翻转单链表（空间O(n)）
/// - Parameter head: 链表头节点
/// - Returns: 翻转后的头节点
func reverseListRecursive(_ head: ListNode?) -> ListNode? {
    // 终止条件：空节点或最后一个节点
    guard let head = head, let next = head.next else {
        return head
    }
    
    // 递归翻转后续链表
    let newHead = reverseListRecursive(next)
    // 翻转当前节点的指向
    next.next = head
    head.next = nil
    
    return newHead
}

/// 辅助函数：打印链表
func printList(_ head: ListNode?) {
    var curr = head
    var result = ""
    while curr != nil {
        result += "\(curr!.val)"
        if curr?.next != nil {
            result += "→"
        }
        curr = curr?.next
    }
    print(result)
}

/// 辅助函数：构建链表
func buildList(_ nums: [Int]) -> ListNode? {
    guard !nums.isEmpty else {
        return nil
    }
    let head = ListNode(nums[0])
    var curr = head
    for i in 1..<nums.count {
        let node = ListNode(nums[i])
        curr.next = node
        curr = node
    }
    return head
}

// 测试案例
func testReverseList() {
    // 构建测试链表：1→2→3→4→5
    let originalList = buildList([1,2,3,4,5])
    print("原链表：", terminator: "")
    printList(originalList)
    
    // 测试迭代法
    let reversedIterative = reverseListIterative(originalList)
    print("迭代法翻转后：", terminator: "")
    printList(reversedIterative)
    // 验证：5→4→3→2→1
    assert(reversedIterative?.val == 5, "迭代法测试失败1")
    assert(reversedIterative?.next?.val == 4, "迭代法测试失败2")
    assert(reversedIterative?.next?.next?.next?.next?.val == 1, "迭代法测试失败3")
    assert(reversedIterative?.next?.next?.next?.next?.next == nil, "迭代法测试失败4")
    
    // 重建链表测试递归法
    let originalList2 = buildList([1,2,3,4,5])
    let reversedRecursive = reverseListRecursive(originalList2)
    print("递归法翻转后：", terminator: "")
    printList(reversedRecursive)
    // 验证
    assert(reversedRecursive?.val == 5, "递归法测试失败1")
    assert(reversedRecursive?.next?.val == 4, "递归法测试失败2")
    
    // 测试空链表
    assert(reverseListIterative(nil) == nil, "空链表测试失败1")
    assert(reverseListRecursive(nil) == nil, "空链表测试失败2")
    
    // 测试单节点链表
    let singleNode = ListNode(6)
    assert(reverseListIterative(singleNode)?.val == 6, "单节点测试失败1")
    assert(reverseListRecursive(singleNode)?.val == 6, "单节点测试失败2")
    
    print("所有测试用例通过！")
}

// 执行测试
testReverseList()

三、逻辑验证（迭代法）

链表 1→2→3→4→5 的翻转过程：

prev=nil, curr=1 → temp=2，1.next=nil → prev=1, curr=2；
temp=3，2.next=1 → prev=2, curr=3；
temp=4，3.next=2 → prev=3, curr=4；
temp=5，4.next=3 → prev=4, curr=5；
temp=nil，5.next=4 → prev=5, curr=nil；
循环结束，prev=5 为新头节点（正确）。

四、关键细节与边界处理

临时指针 ：必须保存 curr.next，否则翻转后丢失后续节点；
递归终止条件：空节点或最后一个节点直接返回，避免无限递归；
单节点/空链表：直接返回原节点/nil，无需处理。

五、面试加分点与记忆法

加分点

算法对比：迭代法空间 O(1) 优于递归法（O(n)），推荐工程使用；
时间复杂度：两种方法均为 O(n)（遍历所有节点）；
扩展思考：实现部分翻转（如翻转第 m 到 n 个节点）。

记忆法

迭代法记忆法："prev空，curr头，存temp，翻指向，prev移curr，curr移temp，curr空时prev是头"；
递归法记忆法："递归到尾部，从后往前翻，next指向当前，当前指向nil，返回新头"。

请说明哈希表的核心原理，并引申介绍红黑树、二叉搜索树的特点及区别。

一、哈希表的核心原理

哈希表（Hash Table）是一种基于"键-值"存储的数据结构，核心目标是O(1) 时间复杂度的增删改查，其核心原理分为三部分：

哈希函数（Hash Function）

哈希函数是哈希表的核心，作用是将任意长度的"键（Key）"转换为固定长度的"哈希值（Hash Value）"，映射到哈希表的数组索引。

核心要求 ：
- 确定性：同一键必须返回同一哈希值；
- 均匀性：哈希值均匀分布，减少冲突；
- 高效性：计算速度快（如取模、位运算）。
常见哈希函数 ：
- 取模法：hash(key) = key % 数组长度；
- 位运算法：hash(key) = (key >> 16) ^ key（混合高低位）；
- 字符串哈希：hash = hash * 31 + char（31 是质数，减少冲突）。

哈希冲突（Hash Collision）

由于哈希值范围有限，不同键可能映射到同一索引（冲突），常见解决方法：

解决方法	原理	优点	缺点
链地址法（拉链法）	数组每个索引对应一个链表/红黑树，冲突元素存入链表/树	实现简单，扩容方便	链表过长时查询效率降为 O(n)
开放定址法	冲突时按规则（线性探测、二次探测）寻找下一个空位置	无需额外空间	易产生聚集，删除复杂
再哈希法	冲突时使用另一个哈希函数计算新索引	减少聚集	计算成本高

扩容（Rehash）

当哈希表的负载因子（已存储元素数/数组长度）超过阈值（通常 0.75），需扩容数组并重新计算所有元素的哈希值：

步骤：创建新数组（长度通常翻倍）→ 遍历旧数组 → 重新哈希元素到新数组 → 释放旧数组；
目的：降低负载因子，减少冲突，保证查询效率。

核心特性

理想时间复杂度：增删改查 O(1)；
最坏时间复杂度：O(n)（所有元素冲突，链表遍历）；
空间复杂度：O(n)（数组+冲突存储结构）；
无序性：元素存储顺序与插入顺序无关。

二、二叉搜索树（BST）的特点

二叉搜索树是基于二叉树的有序数据结构，核心规则：

节点规则 ：
- 左子树所有节点值 < 当前节点值；
- 右子树所有节点值 > 当前节点值；
- 左右子树均为二叉搜索树。
核心操作 ：
- 查找：从根节点开始，比当前小查左，比当前大查右，相等则找到；
- 插入：按查找规则找到空位置插入；
- 删除：分三种情况（叶子节点、单子树节点、双子树节点）。
特性：
- 中序遍历结果为有序序列；
- 理想时间复杂度：增删改查 O(log n)（平衡树）；
- 最坏时间复杂度：O(n)（退化为链表，如插入有序数据）；
- 无自动平衡机制，易倾斜。

三、红黑树（Red-Black Tree）的特点

红黑树是自平衡的二叉搜索树，在BST基础上增加颜色规则保证平衡：

颜色规则 ：
- 每个节点为红/黑；
- 根节点为黑；
- 叶子节点（nil）为黑；
- 红节点的子节点必为黑（无连续红节点）；
- 从任意节点到其叶子节点的所有路径，黑节点数相同。
平衡机制 ：插入/删除时通过旋转（左旋/右旋） 和变色维持规则，保证树的高度不超过 2log(n+1)。
特性：
- 绝对平衡：高度差不超过2倍，避免退化为链表；
- 时间复杂度：增删改查 O(log n)（稳定）；
- 空间复杂度：O(n)（存储颜色信息）；
- 有序性：中序遍历有序。

四、哈希表、红黑树、二叉搜索树的区别

维度	哈希表	二叉搜索树	红黑树
有序性	无序	有序（中序遍历）	有序（中序遍历）
平均时间复杂度	增删改查 O(1)	增删改查 O(log n)	增删改查 O(log n)
最坏时间复杂度	O(n)（冲突严重）	O(n)（倾斜）	O(log n)（稳定）
空间复杂度	O(n)（数组+冲突结构）	O(n)	O(n)（颜色信息）
适用场景	快速查找、无序存储（如字典、缓存）	有序存储、简单场景（数据量小）	有序存储、高性能场景（如 TreeMap、C++ map）
插入/删除成本	低（理想O(1)）	低（无平衡）	中（旋转+变色）
遍历效率	低（无序，需遍历所有元素）	中（中序遍历O(n)）	中（中序遍历O(n)）

五、面试加分点与记忆法

加分点

工程应用：
- 哈希表：Swift Dictionary、 HashMap（拉链法，冲突链表长度>8转红黑树）；
- 红黑树： TreeMap、Linux 内核调度；
- BST：简单有序场景，极少单独使用（易倾斜）；
深度理解：解释 HashMap 为何冲突链表长度>8转红黑树（O(log n) 优于 O(n)）；
扩展思考：对比跳表（Redis Zset）与红黑树的优劣。

记忆法

哈希表记忆法："哈希函数映射索引，冲突用拉链/开放定址，扩容降负载，O(1) 查改，无序"；
BST记忆法："左小右大，中序有序，理想O(log n)，最坏链表O(n)"；
红黑树记忆法："BST+颜色规则，旋转变色保平衡，稳定O(log n)，有序高性能"；
区别记忆法："哈希快但无序，红黑树有序且稳定，BST简单但易倾斜"。

有 N 个地点需要修路，要求修路总长度最小，该问题应如何解决？（补充：涉及最小生成树算法）

一、问题本质与核心思路

该问题属于图论中的最小生成树（Minimum Spanning Tree，MST） 问题：将 N 个地点抽象为图的顶点，地点间的修路长度抽象为顶点间的边权值，需找到一组边，连接所有顶点且无环，同时总权值（修路总长度）最小。核心解决算法有两种------Kruskal 算法和 Prim 算法，以下从算法原理、实现逻辑、适用场景全维度解析。

二、最小生成树的核心定义

生成树：包含图中所有顶点，且边数为顶点数-1，无环的子图；
最小生成树：所有生成树中，边权值总和最小的生成树；
核心性质 ：
- 唯一性：若所有边权值不同，MST 唯一；若存在相同权值，可能有多个 MST，但总权值相同；
- 无环性：MST 中任意两点间有且仅有一条路径。

三、解决方案1：Kruskal 算法（按边贪心）

算法原理

Kruskal 算法基于"边贪心"策略，核心是按边权值从小到大排序，依次选择边，若该边连接的两个顶点不在同一连通分量中（避免环），则加入 MST，直到 MST 包含所有顶点。

核心步骤
构建边集：将所有地点间的修路长度（边）整理为集合，每条边包含"顶点A、顶点B、权值"；
边排序：按权值从小到大排序所有边；
连通性检查 ：使用并查集（Union-Find）数据结构，判断当前边的两个顶点是否已连通：
- 若未连通：将边加入 MST，合并两个顶点的连通分量；
- 若已连通：跳过该边（避免环）；
终止条件：MST 中的边数达到 N-1（N 为顶点数），停止遍历。

Swift 核心实现（简化版）

// 并查集实现（用于连通性检查）
class UnionFind {
private var parent: [Int]
init(_ count: Int) {
parent = Array(0..<count)
}

复制代码

 // 查找根节点（路径压缩）
 func find(_ x: Int) -> Int {
     if parent[x] != x {
         parent[x] = find(parent[x])
     }
     return parent[x]
 }
 
 // 合并两个连通分量
 func union(_ x: Int, _ y: Int) {
     let rootX = find(x)
     let rootY = find(y)
     if rootX != rootY {
         parent[rootY] = rootX
     }
 }
 
 // 判断是否连通
 func isConnected(_ x: Int, _ y: Int) -> Bool {
     return find(x) == find(y)
 }

}

// 边结构
struct Edge {
let from: Int // 起点（地点编号）
let to: Int // 终点
let weight: Int // 修路长度
}

// Kruskal 算法实现
func kruskalMST(_ edges: [Edge], _ vertexCount: Int) -> ([Edge], Int) {
// 1. 按权值排序边
let sortedEdges = edges.sorted { $0.weight <$ 1.weight }
let uf = UnionFind(vertexCount)
var mstEdges: [Edge] = []
var totalWeight = 0

复制代码

 // 2. 遍历排序后的边
 for edge in sortedEdges {
     guard mstEdges.count < vertexCount - 1 else { break }
     if !uf.isConnected(edge.from, edge.to) {
         uf.union(edge.from, edge.to)
         mstEdges.append(edge)
         totalWeight += edge.weight
     }
 }
 
 // 验证是否连通所有顶点（避免图不连通）
 guard mstEdges.count == vertexCount - 1 else {
     fatalError("图不连通，无法构建最小生成树")
 }
 
 return (mstEdges, totalWeight)

}

// 测试案例
func testKruskal() {
// 顶点：0,1,2,3（4个地点）
// 边：(0-1,1), (0-2,3), (1-2,1), (1-3,5), (2-3,2)
let edges = [
Edge(from: 0, to: 1, weight: 1),
Edge(from: 0, to: 2, weight: 3),
Edge(from: 1, to: 2, weight: 1),
Edge(from: 1, to: 3, weight: 5),
Edge(from: 2, to: 3, weight: 2)
]

复制代码

 let (mst, total) = kruskalMST(edges, 4)
 print("MST 边：")
 mst.forEach { print("(\($0.from)-\($0.to), \($0.weight))") }
 print("总长度：\(total)") // 输出：1+1+2=4（正确）

}

testKruskal()

四、解决方案2：Prim 算法（按顶点贪心）

算法原理

Prim 算法基于"顶点贪心"策略，从任意顶点出发，每次选择与当前 MST 连通的边中权值最小的边，将对应顶点加入 MST，直到包含所有顶点。

核心步骤
初始化：选择一个起始顶点加入 MST，维护两个集合（已加入 MST 的顶点、未加入的顶点）；
找最小边：遍历所有"已加入顶点→未加入顶点"的边，选择权值最小的边；
扩展 MST：将该边的未加入顶点加入 MST，累加权值；
终止条件：MST 包含所有顶点。
适用场景对比

算法	核心策略	时间复杂度	适用场景
Kruskal	按边排序，并查集判连通	O(E log E)（E 为边数）	稀疏图（地点多、修路路径少）
Prim	按顶点扩展，邻接矩阵/堆	O(V²)（邻接矩阵）/ O(E log V)（堆优化）	稠密图（地点少、修路路径多）

五、关键细节与面试加分点

并查集的优化：Kruskal 算法的效率依赖并查集，路径压缩（find 时）和按秩合并（union 时）可将并查集操作复杂度降至近似 O(1)；
图的连通性：若输入的图不连通（如存在孤立地点），无法构建 MST，需提前校验；
工程落地：实际修路场景中，需考虑边的"不可达性"（如河流、山脉），需过滤无效边；
加分点 ：
- 对比两种算法的底层实现，解释稀疏/稠密图的选择逻辑；
- 提及 MST 的实际应用（如电网铺设、通信基站组网）；
- 扩展思考：若修路有额外约束（如某两个地点必须连通），如何调整算法。

记忆法推荐

Kruskal 记忆法："边排序，查连通，不连通就加，凑够N-1条边"；
Prim 记忆法："选起点，找最小边，扩顶点，直到全覆盖"；
核心记忆法："最小生成树，无环连所有，Kruskal 管稀疏，Prim 管稠密"。

请说明 "上台阶问题"（动态规划入门题）的解题思路。

一、问题描述与核心分析

上台阶问题的经典描述："有 n 级台阶，每次可以上 1 级或 2 级，问有多少种不同的方法登上第 n 级台阶？" 该问题是动态规划（DP）的入门题，核心是通过"状态定义→状态转移→初始条件"三步拆解问题，将复杂问题转化为子问题的叠加。

二、核心解题思路：动态规划

状态定义

设 dp[i] 表示"登上第 i 级台阶的方法数"，核心是找到 dp[i] 与前序状态的关系。

状态转移方程推导

要登上第 i 级台阶，最后一步只有两种可能：

从第 i-1 级台阶上 1 级到达：方法数为 dp[i-1]；
从第 i-2 级台阶上 2 级到达：方法数为 dp[i-2]；因此状态转移方程：dp[i] = dp[i-1] + dp[i-2]（本质是斐波那契数列）。

初始条件

当 i=1 时：只有 1 种方法（上 1 级）→ dp[1] = 1；
当 i=2 时：有 2 种方法（1+1 或 2）→ dp[2] = 2；
特殊情况：i=0（地面）→ dp[0] = 1（空操作，作为递推基础）。

三、具体实现方式（从基础到优化）

基础版：递归（暴力解法，存在重复计算）

func climbStairsRecursive(_ n: Int) -> Int {
if n == 1 { return 1 }
if n == 2 { return 2 }
return climbStairsRecursive(n-1) + climbStairsRecursive(n-2)
}

问题：时间复杂度 O(2ⁿ)（大量重复计算，如计算 dp[5] 需重复计算 dp[3]）；
优化：记忆化递归（缓存已计算的结果）。

优化版1：记忆化递归（Top-Down）

func climbStairsMemo(_ n: Int) -> Int {
var memo: [Int: Int] = [0:1, 1:1, 2:2] // 缓存
func dp(_ i: Int) -> Int {
if let val = memo[i] { return val }
let res = dp(i-1) + dp(i-2)
memo[i] = res
return res
}
return dp(n)
}

时间复杂度 O(n)，空间复杂度 O(n)（缓存+递归栈）。

优化版2：迭代动态规划（Bottom-Up）

func climbStairsDP(_ n: Int) -> Int {
guard n >= 1 else { return 0 }
if n == 1 { return 1 }
var dp = Array(repeating: 0, count: n+1)
dp[1] = 1
dp[2] = 2
for i in 3...n {
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}

时间复杂度 O(n)，空间复杂度 O(n)（dp 数组）。

终极优化：空间压缩（仅保留前两个状态）

func climbStairsOpt(_ n: Int) -> Int {
guard n >= 1 else { return 0 }
if n == 1 { return 1 }
var prev1 = 1 // dp[i-2]
var prev2 = 2 // dp[i-1]
for _ in 3...n {
let current = prev1 + prev2
prev1 = prev2
prev2 = current
}
return prev2
}

时间复杂度 O(n)，空间复杂度 O(1)（仅用两个变量）。

四、扩展场景（面试高频变种）

变种1：每次可上 1、2、3 级台阶

状态转移方程：dp[i] = dp[i-1] + dp[i-2] + dp[i-3]；初始条件：dp[1]=1, dp[2]=2, dp[3]=4。

变种2：每次可上 k 级台阶（k 为给定值）

状态转移方程：dp[i] = sum(dp[i-j])（j 从 1 到 min(k, i)）；初始条件：dp[0]=1, dp[1]=1。

变种3：某些台阶不可踩（如第 m 级台阶禁止）

状态转移时跳过不可踩台阶：

复制代码

func climbStairsWithForbidden(_ n: Int, _ forbidden: [Int]) -> Int {
    guard n >= 1 else { return 0 }
    var dp = Array(repeating: 0, count: n+1)
    dp[1] = forbidden.contains(1) ? 0 : 1
    if n >= 2 {
        dp[2] = forbidden.contains(2) ? 0 : (dp[1] + (forbidden.contains(0) ? 0 : 1))
    }
    for i in 3...n {
        if forbidden.contains(i) {
            dp[i] = 0
        } else {
            dp[i] = dp[i-1] + dp[i-2]
        }
    }
    return dp[n]
}

五、面试加分点与记忆法

加分点

动态规划的核心思想："最优子结构+重叠子问题"，上台阶问题中，dp[i] 的最优解依赖子问题 dp[i-1] 和 dp[i-2]，且子问题重复出现；
复杂度分析：从递归的 O(2ⁿ) 优化到空间压缩的 O(1)，体现算法优化思路；
数学本质：上台阶问题等价于斐波那契数列（dp[n] = F(n+1)，F 为斐波那契数列）。

记忆法推荐
核心公式记忆法："dp[i] = dp[i-1] + dp[i-2]，初始1和2，n≥3递推"；
优化思路记忆法："递归有重复，记忆化缓存，DP用数组，压缩省空间"；
变种记忆法："多步加项数，禁踩置为0"。

若可用内存仅 1G，已加载 800M 的程序，需运行另一个 400M 的程序，该如何处理？

一、问题核心分析

可用内存 1G（1024M），已占用 800M，剩余 224M，而新程序需 400M，核心矛盾是物理内存不足，需通过操作系统的内存管理机制、程序优化手段解决，核心思路分为"系统层调度"和"应用层优化"两类。

二、系统层解决方案（依赖操作系统调度）

虚拟内存（Virtual Memory）+ 交换分区（Swap）

原理：操作系统将部分硬盘空间模拟为"虚拟内存"，当物理内存不足时，将当前程序中不活跃的内存页（如已加载但未使用的代码、数据）换出到硬盘的交换分区，释放物理内存，再加载新程序的内存页；
执行逻辑 ：
1. 系统检测到物理内存不足，触发"页面置换算法"（如 LRU、LFU）；
2. 将已加载程序（800M）中不活跃的内存页（至少 176M）换出到 Swap；
3. 物理内存剩余 ≥400M，加载新程序；
4. 当被换出的内存页需要访问时，再将新程序中不活跃的页换出，换回原页；
优缺点 ：
- 优点：无需修改程序，系统自动处理；
- 缺点：硬盘 IO 速度远低于内存，频繁换入换出会导致"内存抖动"（Thrashing），程序运行卡顿。

内存压缩（Memory Compression）

原理：iOS/macOS 等系统支持内存压缩，将不活跃的内存页压缩后存储在物理内存中，而非换出到硬盘，压缩比通常可达 2:1~4:1；
执行逻辑 ：
1. 系统压缩已加载程序的 800M 内存中不活跃的部分（如 400M 压缩为 100M）；
2. 物理内存释放 300M，剩余 224+300=524M ≥400M，加载新程序；
3. 访问压缩页时，系统实时解压，速度远快于 Swap；
适用场景：macOS（ZRAM）、iOS（内存压缩框架），比 Swap 更高效。

终止低优先级进程

原理：系统根据进程优先级，终止后台低优先级进程（如缓存进程、闲置应用），释放物理内存；
执行逻辑 ：
1. 系统遍历进程列表，终止优先级低于当前待运行程序的进程；
2. 释放的内存 + 剩余物理内存 ≥400M，加载新程序；
注意：仅适用于多进程系统，若 800M 为当前唯一活跃进程，无法通过此方式释放内存。

三、应用层解决方案（修改程序/运行策略）

程序内存分段加载（按需加载）

原理：将 400M 的新程序拆分为多个段（如代码段、数据段、资源段），仅加载当前运行必需的段，非必需段（如静态资源、未执行的代码）延迟加载；
执行逻辑 ：
1. 新程序核心逻辑仅需 200M，先加载核心段，占用 200M 物理内存；
2. 运行过程中，当需要访问非核心段时，再将已加载程序的不活跃页换出，加载对应段；
3. 执行完成后，释放非核心段内存；
落地方式 ：
- 代码层面：使用动态库（Dylib），按需加载；
- 资源层面：图片、视频等资源延迟加载，使用时从硬盘读取，用完释放。

内存优化（减少程序实际占用）

针对已加载程序（800M） ：
1. 释放未使用的缓存（如图片缓存、数据缓存）；
2. 回收大对象（如未使用的数组、字典），将临时数据写入硬盘（如 ite）；
3. 压缩内存中的数据（如 JSON 字符串、日志）；
针对新程序（400M） ：
1. 优化数据结构（如用结构体替代类，减少内存开销）；
2. 复用对象（如对象池模式），避免重复创建大对象；
3. 懒加载（Lazy Loading）：延迟初始化非必需对象，仅在使用时创建；
效果：若已加载程序优化后占用降至 600M，剩余物理内存 424M ≥400M，可直接加载新程序。

分阶段运行程序

原理：将新程序的执行逻辑拆分为多个阶段，每个阶段仅加载所需内存，执行完一个阶段后释放对应内存，再执行下一个阶段；
执行逻辑 ：
1. 新程序阶段1：需 200M 内存，加载并执行，占用 200M；
2. 执行完成后，释放阶段1的 200M 内存；
3. 加载阶段2：需 200M 内存，执行并释放；
4. 依次完成所有阶段，全程仅占用 200M 物理内存；
适用场景：新程序为批处理任务（如数据解析、文件转换），可拆分阶段。

使用内存映射（MMAP）

原理：将新程序的大文件（如数据文件）通过内存映射映射到虚拟内存，而非一次性加载到物理内存，仅在访问对应区域时加载该页；
执行逻辑 ：
1. 新程序的 400M 中，若 300M 为数据文件，通过 mmap 映射，仅占用少量虚拟内存空间；
2. 实际物理内存仅需加载 100M 核心代码，剩余 224-100=124M 足够；
3. 访问数据文件时，系统自动加载对应内存页，用完后置换；
优点：避免一次性加载大文件，减少物理内存占用。

四、面试加分点与注意事项

加分点

区分"物理内存"与"虚拟内存"：虚拟内存不受物理内存限制，但访问速度依赖物理内存；
页面置换算法：解释 LRU（最近最少使用）、LFU（最不经常使用）的核心逻辑，说明系统如何选择换出的内存页；
跨平台差异：iOS 无用户可配置的 Swap，依赖内存压缩；macOS/Linux 支持 Swap 配置；
性能权衡：内存压缩 > 分段加载 > Swap，优先选择低 IO 开销的方案。

注意事项

避免频繁内存置换：过度依赖 Swap 会导致程序响应缓慢，需结合应用层优化；
内存泄漏检查：已加载程序的 800M 可能包含内存泄漏，需先排查泄漏，释放无效内存；
优先级管理：确保核心程序不被系统终止，新程序若为非核心，可降低优先级。

记忆法推荐

核心思路记忆法："系统层靠置换（Swap）、压缩、终止进程；应用层靠分段、优化、映射、分阶段"；
优先级记忆法："内存压缩优先，其次分段加载，最后 Swap，避免抖动保性能"。

LRU（最近最少使用）缓存机制如何实现？

一、LRU 核心定义与原理

LRU（Least Recently Used）是一种缓存淘汰策略，核心规则是"当缓存容量达到上限时，淘汰最近最少使用的缓存项"，广泛应用于操作系统页面置换、Redis 缓存、数据库缓存等场景。其核心需求：

快速查找：O(1) 时间找到缓存项；
快速更新：O(1) 时间标记缓存项为"最近使用"；
快速淘汰：O(1) 时间删除最近最少使用的项；
有序性：维护缓存项的使用时间顺序。

二、核心实现方案：哈希表 + 双向链表

数据结构选择原因

哈希表（Dictionary）：实现 O(1) 查找缓存项（键→节点）；
双向链表：维护缓存项的使用顺序，表头为"最近使用"，表尾为"最近最少使用"，支持 O(1) 插入/删除节点；
组合优势：哈希表保证查找效率，双向链表保证更新/淘汰效率。

核心操作逻辑

操作	执行步骤	时间复杂度
查找（get）	1. 哈希表查找键对应的节点；2. 若存在：将节点移到链表头部（标记为最近使用），返回值；3. 若不存在：返回 nil	O(1)
插入（put）	1. 哈希表查找键：- 存在：更新值，将节点移到链表头部；- 不存在：a. 创建新节点，加入哈希表，插入链表头部；b. 若缓存容量超限：删除链表尾部节点（最近最少使用），并从哈希表移除；	O(1)
淘汰	直接删除链表尾部节点，哈希表同步移除	O(1)

Swift 完整实现

// 双向链表节点
class DLinkedNode {
let key: Int
var value: Int
var prev: DLinkedNode?
var next: DLinkedNode?

复制代码

 init(key: Int, value: Int) {
     self.key = key
     self.value = value
 }

}

// LRU 缓存实现
class LRUCache {
private let capacity: Int // 缓存容量
private var cache: [Int: DLinkedNode] // 哈希表：key → 节点
private let head: DLinkedNode // 虚拟头节点（最近使用）
private let tail: DLinkedNode // 虚拟尾节点（最近最少使用）

复制代码

 init(_ capacity: Int) {
     self.capacity = max(capacity, 1) // 容量至少为1
     self.cache = [:]
     
     // 初始化虚拟头尾节点，避免空指针
     self.head = DLinkedNode(key: -1, value: -1)
     self.tail = DLinkedNode(key: -1, value: -1)
     head.next = tail
     tail.prev = head
 }
 
 // 查找缓存
 func get(_ key: Int) -> Int? {
     guard let node = cache[key] else {
         return nil // 缓存未命中
     }
     // 将节点移到头部（标记为最近使用）
     moveToHead(node)
     return node.value
 }
 
 // 插入/更新缓存
 func put(_ key: Int, _ value: Int) {
     if let node = cache[key] {
         // 缓存命中：更新值，移到头部
         node.value = value
         moveToHead(node)
     } else {
         // 缓存未命中：创建新节点
         let newNode = DLinkedNode(key: key, value: value)
         cache[key] = newNode
         addToHead(newNode)
         
         // 容量超限：删除尾部节点
         if cache.count > capacity {
             let removedNode = removeTail()
             cache.removeValue(forKey: removedNode.key)
         }
     }
 }
 
 // MARK: - 链表辅助方法
 // 添加节点到头部（虚拟头节点之后）
 private func addToHead(_ node: DLinkedNode) {
     node.prev = head
     node.next = head.next
     head.next?.prev = node
     head.next = node
 }
 
 // 移除指定节点
 private func removeNode(_ node: DLinkedNode) {
     node.prev?.next = node.next
     node.next?.prev = node.prev
 }
 
 // 将节点移到头部（先移除，再添加）
 private func moveToHead(_ node: DLinkedNode) {
     removeNode(node)
     addToHead(node)
 }
 
 // 移除尾部节点（虚拟尾节点之前）
 private func removeTail() -> DLinkedNode {
     guard let realTail = tail.prev, realTail !== head else {
         fatalError("缓存为空，无法删除")
     }
     removeNode(realTail)
     return realTail
 }
 
 // 打印缓存（调试用）
 func printCache() {
     var current = head.next
     var result = "LRU Cache: "
     while current !== tail {
         result += "(\(current!.key):\(current!.value)) → "
         current = current?.next
     }
     result += "nil"
     print(result)
 }

}

// 测试案例
func testLRUCache() {
let lru = LRUCache(3) // 容量3

复制代码

 // 插入3个元素：1→2→3
 lru.put(1, 10)
 lru.put(2, 20)
 lru.put(3, 30)
 lru.printCache() // (3:30) → (2:20) → (1:10) → nil
 
 // 查找1，移到头部
 _ = lru.get(1)
 lru.printCache() // (1:10) → (3:30) → (2:20) → nil
 
 // 插入4，容量超限，删除尾部（2）
 lru.put(4, 40)
 lru.printCache() // (4:40) → (1:10) → (3:30) → nil
 
 // 查找2，未命中
 assert(lru.get(2) == nil, "测试失败：查找已淘汰的2应返回nil")
 
 // 更新3的值，移到头部
 lru.put(3, 300)
 lru.printCache() // (3:300) → (4:40) → (1:10) → nil
 
 print("所有测试用例通过！")

}

testLRUCache()

三、关键细节与边界处理

虚拟头尾节点

引入虚拟头（head）和虚拟尾（tail）节点，避免处理"空链表""头节点/尾节点为空"的边界情况，简化插入/删除逻辑；
真实节点始终在虚拟头尾之间，无需判断节点是否为头/尾。

哈希表与链表的同步

插入节点时：哈希表和链表必须同时添加；
删除节点时：哈希表和链表必须同时移除；
更新节点时：仅更新链表中节点的位置，哈希表无需修改（键未变）。

容量校验

初始化时确保容量 ≥1，避免无效容量；
插入新节点后，若缓存数量 > 容量，立即淘汰尾部节点。

四、扩展优化与面试加分点

优化方向

线程安全 ：添加读写锁（如 pthread_rwlock_t），保证多线程环境下的操作安全；
时间复杂度优化：当前实现已达 O(1)，无进一步优化空间；
空间优化 ：使用自定义链表而非系统容器（如 LinkedList），减少额外开销。

工程应用

Redis LRU：Redis 的 LRU 实现并非严格的双向链表，而是通过"近似 LRU"（随机采样）减少内存开销；
iOS 应用：图片缓存、网络请求缓存可基于 LRU 实现，避免缓存无限增长；
操作系统：页面置换算法中的 LRU 用于选择换出的内存页。

加分点

对比其他缓存策略：
- LFU（最不经常使用）：淘汰访问次数最少的项，需额外记录访问次数；
- FIFO（先进先出）：淘汰最先插入的项，实现简单但未考虑使用频率；
解释 LRU 的核心优势："利用局部性原理"，最近使用的项大概率会再次使用；
边界场景分析：空缓存、容量为1、重复插入同一键、查找已淘汰的键。

记忆法推荐

核心结构记忆法："哈希表找节点，双向链表排顺序，头是最近用，尾是最少用，满了删尾巴"；
操作记忆法："get查哈希，有就移到头；put查哈希，有就更值移头，无就加头，满了删尾"；
优化记忆法："虚拟头尾避边界，哈希链表要同步，线程安全加锁"。

有两个大文件，均存储 URL 数据，如何快速找出两个文件中相同的 URL？（提示：可使用布隆过滤器）

一、问题核心分析

两个大文件（如各 10G）存储 URL，核心痛点是"文件过大，无法一次性加载到内存"，需通过"分治+哈希+布隆过滤器"组合方案，在时间和空间效率间平衡，快速找出交集 URL。

二、核心解决方案（分阶段实现）

阶段1：文件分片（分治思想，解决内存不足）

原理：将大文件按哈希值拆分为多个小文件（如每个小文件 ≤1G），保证相同 URL 必然落在同一小文件中，将"大文件交集"转化为"多个小文件交集"；
执行步骤 ：
1. 定义哈希函数 hash(url) = url 的哈希值 % N（N 为分片数，如 N=10，拆分为 10 个小文件）；
2. 遍历文件 A 的所有 URL，按 hash(url) 将 URL 写入对应小文件 A0~A9；
3. 遍历文件 B 的所有 URL，按相同哈希函数写入对应小文件 B0~B9；
4. 此时，A_i 和 B_i 中的 URL 哈希值相同，仅需对比 A_i 和 B_i 即可找到交集（相同 URL 必在同一对小文件中）；
关键：哈希函数需均匀分布 URL，避免某小文件过大（可调整 N 或哈希函数）。

阶段2：布隆过滤器快速过滤（减少对比量）

原理：布隆过滤器（Bloom Filter）是空间高效的概率型数据结构，可快速判断"元素是否存在"（假阳性率可控，无假阴性）；
执行步骤 ：
1. 选择一个小文件对（如 A0 和 B0），读取 A0 的所有 URL，插入布隆过滤器；
2. 遍历 B0 的每个 URL，用布隆过滤器判断是否存在：
  - 不存在：直接跳过；
  - 存在：加入"候选 URL 列表"（需进一步验证）；
布隆过滤器参数选择 ：
- 假阳性率 p（如 0.01）、元素数量 n（A0 的 URL 数），计算所需位数 m 和哈希函数个数 k：
  - m = -n * ln(p) / (ln2)²（位数）；
  - k = m/n * ln2（哈希函数数）；
- 示例：n=1000 万，p=0.01 → m≈958 万位（≈1.17MB），k=7。

阶段3：精确校验（消除布隆过滤器假阳性）

原理：布隆过滤器的"存在"可能为假阳性，需对候选 URL 精确校验；
执行步骤 ：
1. 将 A0 的 URL 存入哈希表（如 Swift Dictionary），占用内存 ≤1G；
2. 遍历候选 URL 列表，查询哈希表：
  - 存在：确认为交集 URL，写入结果文件；
  - 不存在：排除（布隆过滤器假阳性）；
3. 对所有小文件对（A1&B1~A9&B9）重复阶段2~3，汇总所有交集 URL。

三、完整实现流程（伪代码）

复制代码

// 步骤1：文件分片
func splitFile(_ filePath: String, _ outputDir: String, _ splitCount: Int) {
    let file = FileHandle(forReadingAtPath: filePath)!
    defer { file.closeFile() }
    
    // 创建 splitCount 个输出文件句柄
    var outputHandles: [FileHandle] = []
    for i in 0..<splitCount {
        let path = "\(outputDir)/part\(i).txt"
        FileManager.default.createFile(atPath: path, contents: nil)
        outputHandles.append(FileHandle(forWritingAtPath: path)!)
    }
    
    // 按哈希分片
    while let line = file.readLine() { // 读取一行（一个URL）
        let url = line.trimmingCharacters(in: .whitespaces)
        let hashValue = hashURL(url) % splitCount
        outputHandles[hashValue].write("\(url)\n".data(using: .utf8)!)
    }
    
    // 关闭输出句柄
    outputHandles.forEach { $0.closeFile() }
}

// 步骤2：布隆过滤器过滤 + 步骤3：精确校验
func findIntersection(_ partA: String, _ partB: String) -> [String] {
    // 1. 构建布隆过滤器（A的URL）
    let bloomFilter = BloomFilter(expectedCount: 10_000_000, falsePositiveRate: 0.01)
    let fileA = FileHandle(forReadingAtPath: partA)!
    while let line = fileA.readLine() {
        let url = line.trimmingCharacters(in: .whitespaces)
        bloomFilter.insert(url)
    }
    fileA.closeFile()
    
    // 2. 过滤B的URL，得到候选列表
    var candidates: [String] = []
    let fileB = FileHandle(forReadingAtPath: partB)!
    while let line = fileB.readLine() {
        let url = line.trimmingCharacters(in: .whitespaces)
        if bloomFilter.contains(url) {
            candidates.append(url)
        }
    }
    fileB.closeFile()
    
    // 3. 精确校验（A的URL存入哈希表）
    var urlMap: [String: Bool] = [:]
    let fileA2 = FileHandle(forReadingAtPath: partA)!
    while let line = fileA2.readLine() {
        let url = line.trimmingCharacters(in: .whitespaces)
        urlMap[url] = true
    }
    fileA2.closeFile()
    
    // 4. 筛选真实交集
    let intersection = candidates.filter { urlMap[$0] == true }
    return intersection
}

// 步骤4：汇总所有分片的交集
func findTotalIntersection(_ dirA: String, _ dirB: String, _ splitCount: Int) -> [String] {
    var totalIntersection: [String] = []
    for i in 0..<splitCount {
        let partA = "\(dirA)/part\(i).txt"
        let partB = "\(dirB)/part\(i).txt"
        let partIntersection = findIntersection(partA, partB)
        totalIntersection.append(contentsOf: partIntersection)
    }
    return totalIntersection
}

// 辅助：URL哈希函数（简化版）
func hashURL(_ url: String) -> Int {
    return url.hashValue
}

// 布隆过滤器简化实现
class BloomFilter {
    private var bits: [Bool]
    private let hashFunctions: [(String) -> Int] // 多个哈希函数
    private let bitCount: Int
    
    init(expectedCount: Int, falsePositiveRate: Double) {
        // 计算所需位数和哈希函数数
        let ln2 = log(2)
        self.bitCount = Int(-Double(expectedCount) * log(falsePositiveRate) / (ln2 * ln2))
        let k = Int(Double(self.bitCount) / Double(expectedCount) * ln2)
        
        // 初始化位数组
        self.bits = Array(repeating: false, count: self.bitCount)
        
        // 生成k个哈希函数（简化：基于不同种子）
        self.hashFunctions = (0..<k).map { seed in
            return { url in
                return (url.hashValue + seed) % self.bitCount
            }
        }
    }
    
    // 插入URL
    func insert(_ url: String) {
        for hashFunc in hashFunctions {
            let index = hashFunc(url)
            bits[index] = true
        }
    }
    
    // 判断URL是否存在
    func contains(_ url: String) -> Bool {
        for hashFunc in hashFunctions {
            let index = hashFunc(url)
            if !bits[index] {
                return false // 必不存在
            }
        }
        return true // 可能存在（假阳性）
    }
}

四、关键优化与面试加分点

性能优化

哈希函数选择 ：使用非加密哈希（如 MurmurHash、CityHash），比系统 hashValue 更均匀，减少分片倾斜；
并行处理：多线程处理不同的小文件对（如 A0&B0、A1&B1 并行），提升效率；
磁盘 IO 优化：按块读取文件（而非逐行），减少 IO 次数。

布隆过滤器核心特性

无假阴性：若布隆过滤器返回"不存在"，则 URL 必不在 A 中，可直接跳过；
假阳性可控：通过调整位数 m 和哈希函数数 k，将假阳性率控制在可接受范围（如 1%）；
空间高效：存储 1000 万 URL，假阳性率 1%，仅需约 1.17MB 内存，远低于哈希表（约 800MB）。

替代方案对比

方案	优点	缺点
布隆过滤器+分治	空间高效，速度快	存在假阳性，需精确校验
哈希表直接对比	无假阳性	内存占用大，无法处理超大文件
排序后归并	无需哈希函数	排序耗时，IO 次数多

加分点

解释布隆过滤器的底层原理：多个哈希函数映射到位数组，通过位运算实现快速判断；
分治思想的应用：将大问题拆分为小问题，解决内存不足；
工程落地细节：文件分片时的异常处理（如空文件、超大分片）、哈希冲突的影响。

记忆法推荐

核心流程记忆法："先分片，同哈希进同文件；布隆过滤筛候选，哈希表校验真交集；分片结果汇总，得到所有相同URL"；
布隆过滤器记忆法："多哈希，位数组，无假阴，有假阳，空间省，速度快"；
优化记忆法："哈希均匀防倾斜，并行处理提速度，块读IO更高效"。

给定一个大文件，如何找出其中出现次数最多的十个字符串？

一、问题核心分析

大文件（如 100G）无法一次性加载到内存，核心矛盾是 "内存限制" 与 "统计频次" 的冲突，解决思路需结合分治思想 （拆分文件）+哈希统计 （局部频次）+堆排序（全局 Top10），分阶段实现高效统计。

二、核心解决方案（分四阶段）

阶段 1：文件分片（分治，解决内存不足）

原理：将大文件按固定大小（如 1G）或行数拆分为多个小文件，保证每个小文件可完整加载到内存，将 "全局统计" 转化为 "局部统计 + 结果合并"。
执行步骤 ：
1. 遍历大文件，按字节数 / 行数切割为若干小文件（如 file1.txt、file2.txt...fileN.txt）；
2. 关键优化：若字符串跨分片（如一行未读完），需保证字符串完整性（按换行符 / 分隔符切割），避免统计错误；
3. 示例：100G 文件拆分为 100 个 1G 小文件，每个小文件独立处理。

阶段 2：局部频次统计（哈希表，统计每个小文件的字符串频次）

原理：对每个小文件，加载到内存后用哈希表（如 Dictionary）统计每个字符串的出现次数，输出 "字符串 - 频次" 的临时结果文件。
执行步骤 ：
1. 遍历单个小文件，按分隔符（如空格、换行）拆分字符串；
2. 初始化哈希表 localCount: [String: Int]，遍历字符串：
  - 若字符串已在表中：localCount[str] += 1；
  - 若未在表中：localCount[str] = 1；
3. 统计完成后，将localCount写入临时文件（如 temp1.txt），格式为 "字符串频次"；
4. 对所有小文件重复此步骤，得到 N 个临时频次文件。

Swift 核心代码（局部统计）：

func countLocalFrequency(_ filePath: String, _ outputPath: String) {
guard let file = FileHandle(forReadingAtPath: filePath) else { return }
defer { file.closeFile() }

复制代码

  var localCount: [String: Int] = [:]
  let separator = CharacterSet.whitespacesAndNewlines // 按空白符拆分
  
  // 按块读取文件（避免逐行IO低效）
  while let data = file.readData(ofLength: 4096) { // 4KB块
      guard let content = String(data: data, encoding: .utf8) else { continue }
      let strings = content.components(separatedBy: separator).filter { !$0.isEmpty }
      for str in strings {
          localCount[str, default: 0] += 1
      }
  }
  
  // 写入临时文件
  let outputFile = FileHandle(forWritingAtPath: outputPath)!
  defer { outputFile.closeFile() }
  for (str, count) in localCount {
      let line = "\(str) \(count)\n"
      outputFile.write(line.data(using: .utf8)!)
  }

}

阶段 3：全局频次合并（哈希表 / 堆，合并局部结果）

原理：遍历所有临时频次文件，合并相同字符串的频次，同时维护 "最小堆"（容量 10），实时筛选 Top10，避免存储所有字符串的全局频次（节省内存）。
执行步骤 ：
1. 初始化全局哈希表 globalCount: [String: Int] 和最小堆（堆顶为当前 Top10 中频次最小的元素）；
2. 遍历每个临时频次文件，按行读取 "字符串频次"：
  - 若字符串在globalCount中：globalCount[str] += count；
  - 若未在globalCount中：globalCount[str] = count；
3. 每更新一个字符串的频次，检查是否需加入堆：
  - 若堆大小 < 10：直接加入堆；
  - 若堆大小 = 10 且当前频次 > 堆顶频次：弹出堆顶，加入当前字符串；
最小堆核心逻辑：堆的作用是仅维护当前频次最高的 10 个字符串，无需存储所有字符串的频次（如 100G 文件可能有上亿个不同字符串，堆仅占用极小内存）。

阶段 4：堆排序输出（得到最终 Top10）

原理：最小堆中存储的是 Top10 字符串，但顺序为 "堆顶最小"，需对堆进行排序，输出频次从高到低的结果。
执行步骤 ：
1. 将堆中元素取出，按频次降序排序；
2. 输出排序后的 10 个字符串及其频次，即为最终结果。

三、关键优化与边界处理

性能优化

哈希函数优化：使用高效的字符串哈希（如 MurmurHash），减少哈希冲突，提升统计速度；
并行处理：多线程同时处理不同小文件的局部统计（如 10 线程处理 10 个小文件），提升整体效率；
磁盘 IO 优化：按块读取文件（如 4KB/8KB），减少 IO 调用次数；临时文件写入时批量刷盘，避免频繁写操作。

边界场景处理

超长字符串：若字符串长度超过内存限制，需单独处理（如按哈希分片时，超长字符串单独存储）；
空字符串 / 无效字符：统计前过滤空字符串、不可见字符，避免干扰结果；
重复临时文件：合并时去重（如多个小文件的同一字符串需累加频次）。

替代方案对比

方案	优点	缺点
分治 + 哈希 + 最小堆	内存占用低（仅需存储局部频次和堆），速度快	实现稍复杂，需处理文件分片
直接加载内存统计	实现简单	仅适用于小文件，大文件内存溢出
数据库统计	无需手动处理分片	IO 效率低，依赖数据库性能

四、面试加分点与记忆法

加分点

分治思想的深度应用：将 "无法一次性解决的大问题" 拆分为 "可解决的小问题"，体现算法思维；
堆的选型逻辑：最小堆（而非最大堆）更适合 TopN 问题，因为只需维护 N 个元素，弹出最小元素即可；
工程落地细节：文件分片时的完整性保证、并行处理的线程安全（如临时文件命名避免冲突）。

记忆法推荐
核心流程记忆法："大文件先分片，小文件哈希统计，临时结果合并，最小堆筛 Top10，排序输出终结果"；
堆选型记忆法："TopN 用最小堆，容量固定 N，堆顶是最小，大的进小的出，最后排序降序"；
优化记忆法："分块读 IO 快，并行处理提速度，哈希函数防冲突"。

字符串查找方法（如 KMP、BF 等）的核心原理是什么？

一、基础概念：字符串查找定义

字符串查找（模式匹配）指在 "主串 S" 中查找 "模式串 P" 的首次 / 所有出现位置，核心评价指标是时间复杂度 和空间复杂度，常见算法包括 BF（暴力匹配）、KMP（快速匹配）、BM（博伊尔 - 穆尔）、RK（拉宾 - 卡普）等，以下聚焦核心算法解析。

二、BF 算法（Brute Force，暴力匹配）

核心原理

BF 是最直观的匹配算法，基于 "逐字符比对，失配则回溯"：

步骤 1：主串指针 i 从 0 开始，模式串指针 j 从 0 开始；
步骤 2：若 S [i] == P [j]，则 i++、j++，继续比对；
步骤 3：若 S [i] != P [j]，则 i 回溯到 i-j+1，j 重置为 0，重新比对；
步骤 4：若 j == P.length，匹配成功，返回 i-j；若 i == S.length 且 j < P.length，匹配失败。

代码实现（Swift）

func BFSearch(_ s: String, _ p: String) -> Int? {
let sArr = Array(s), pArr = Array(p)
let sLen = sArr.count, pLen = pArr.count
guard pLen <= sLen else { return nil }

复制代码

 var i = 0, j = 0
 while i < sLen && j < pLen {
     if sArr[i] == pArr[j] {
         i += 1
         j += 1
     } else {
         i = i - j + 1 // 主串指针回溯
         j = 0 // 模式串指针重置
     }
 }
 
 return j == pLen ? i - j : nil

}

特性

时间复杂度：最好 O (n)（一次匹配成功），最坏 O (n*m)（n 为主串长度，m 为模式串长度）；
空间复杂度：O (1)；
优点：实现简单，易于理解；
缺点：失配时主串指针回溯，存在大量重复比对，效率低。

三、KMP 算法（Knuth-Morris-Pratt）

核心原理

KMP 的核心是 "消除主串指针回溯"，通过预处理模式串生成 "部分匹配表（next 数组）"，失配时仅移动模式串指针，利用已匹配的前缀信息跳过无效比对：

核心概念：最长相等前后缀（前缀：不包含最后一个字符的所有子串；后缀：不包含第一个字符的所有子串）；
next 数组定义：next [j] 表示模式串 P [0..j-1] 的最长相等前后缀长度；
匹配逻辑：
1. 预处理模式串生成 next 数组；
2. 主串指针 i 不回溯，模式串指针 j 失配时，跳转到 next [j]（利用最长相等前后缀，跳过已匹配的前缀）；
3. 若 S [i] == P [j]，i++、j++；若 j == P.length，匹配成功；若 i == S.length，匹配失败。

关键步骤：生成 next 数组

func getNext(_ p: String) -> [Int] {
let pArr = Array(p)
let pLen = pArr.count
var next = Array(repeating: 0, count: pLen)
var j = 0 // 前缀指针
for i in 1..<pLen { // i为后缀指针
while j > 0 && pArr[i] != pArr[j] {
j = next[j-1] // 回退到上一个最长相等前后缀
}
if pArr[i] == pArr[j] {
j += 1
}
next[i] = j
}
return next
}

KMP 匹配实现

func KMPSearch(_ s: String, _ p: String) -> Int? {
let sArr = Array(s), pArr = Array(p)
let sLen = sArr.count, pLen = pArr.count
guard pLen <= sLen else { return nil }

复制代码

 let next = getNext(p)
 var j = 0 // 模式串指针
 for i in 0..<sLen { // 主串指针不回溯
     while j > 0 && sArr[i] != pArr[j] {
         j = next[j-1] // 模式串指针跳转到next数组
     }
     if sArr[i] == pArr[j] {
         j += 1
     }
     if j == pLen {
         return i - pLen + 1
     }
 }
 return nil

}

特性

时间复杂度：预处理 O (m)，匹配 O (n)，总 O (n+m)；
空间复杂度：O (m)（存储 next 数组）；
优点：无主串回溯，效率远高于 BF，适合长字符串匹配；
缺点：实现复杂，next 数组生成逻辑较难理解。

四、其他核心算法对比

算法	核心原理	时间复杂度	空间复杂度	适用场景
RK（拉宾 - 卡普）	哈希值比对：计算主串子串和模式串的哈希值，哈希值相等再逐字符校验	最好 O (n+m)，最坏 O (n*m)	O(1)	多模式串匹配、大数据量匹配
BM（博伊尔 - 穆尔）	从模式串尾部向前匹配，利用 "坏字符规则" 和 "好后缀规则" 跳过更多字符	平均 O (n/m)，最坏 O (n*m)	O(1)	实际场景中效率最高（如文本编辑器查找）

五、面试加分点与记忆法

加分点

KMP 的核心优化逻辑："利用最长相等前后缀，避免主串回溯"，解释 next 数组的本质是 "已匹配前缀的复用"；
算法选型：BF 适合短字符串、简单场景；KMP 适合长字符串、高性能场景；BM 适合实际工程（如系统级查找）；
边界场景：模式串为空、主串比模式串短、模式串是主串的前缀 / 后缀。

记忆法推荐
BF 记忆法："逐字符比对，失配回溯 i，重置 j，简单但低效"；
KMP 记忆法："预处理 next 数组，存最长前后缀，失配不回 i，只动 j，高效但复杂"；
核心对比记忆法："BF 回溯主串，KMP 回溯模式串，RK 哈希先比对，BM 从后往前配"。

请简述 TCP 协议的核心特点。

一、TCP 协议的定位

TCP（Transmission Control Protocol，传输控制协议）是基于 IP 协议的面向连接的传输层协议，位于 OSI 七层模型的传输层，核心目标是为应用层提供 "可靠、有序、面向字节流" 的数据传输服务，与 UDP（用户数据报协议）形成互补。

二、TCP 的核心特点（全维度解析）

面向连接（Connection-Oriented）

核心定义：数据传输前必须建立连接，传输完成后释放连接，连接是 "端到端" 的逻辑链路（基于三次握手 / 四次挥手）；
连接特性 ：
- 唯一性：每个 TCP 连接由 "源 IP + 源端口 + 目的 IP + 目的端口" 四元组唯一标识；
- 双向性：连接建立后，双方可同时收发数据（全双工）；
对比 UDP：UDP 无连接，直接发送数据报，无需建立 / 释放连接。

可靠传输（Reliable Transmission）

TCP 通过多机制保证数据可靠送达，核心手段：

确认应答（ACK）：接收方收到数据后，向发送方返回 ACK 报文，确认数据已接收；
重传机制 ：
- 超时重传：发送方发送数据后启动定时器，超时未收到 ACK 则重传；
- 快速重传：接收方收到乱序数据时，连续发送 3 个重复 ACK，发送方立即重传；
序列号与确认号 ：
- 序列号（Sequence Number）：标记数据字节的位置，保证数据有序；
- 确认号（Acknowledgment Number）：表示期望接收的下一个字节的序列号，隐含确认已接收的所有字节；
校验和（Checksum）：发送方计算数据的校验和，接收方校验，检测数据是否损坏；
流量控制：通过滑动窗口机制，避免接收方缓冲区溢出，保证数据接收能力匹配。

有序传输（Ordered Delivery）

核心逻辑：TCP 将数据拆分为报文段，每个报文段携带序列号，接收方按序列号重组数据，若收到乱序报文段，暂存于缓冲区，等待缺失报文段到达后再按序交付给应用层；
对比 UDP：UDP 报文段独立传输，可能乱序，接收方不保证有序。

面向字节流（Byte Stream）

核心定义：TCP 将应用层数据视为连续的字节流，无报文边界（与 UDP 的 "数据报" 不同）；
特性：
- 发送方：应用层写入的数据会被 TCP 缓存，按 MTU（最大传输单元）拆分为报文段发送；
- 接收方：TCP 将收到的报文段重组为字节流，按应用层的读取节奏交付，不保留报文边界；
注意：应用层需自行处理 "粘包" 问题（如定义分隔符、固定长度）。

流量控制（Flow Control）

核心原理：基于滑动窗口（Sliding Window），接收方通过 TCP 报文头的 "窗口大小" 字段，告知发送方自己的接收缓冲区剩余空间，发送方仅发送窗口内的数据，避免接收方缓冲区溢出；
滑动窗口特性：窗口大小动态调整，接收方缓冲区空闲时扩大窗口，满时缩小窗口（甚至置 0，暂停发送）。

拥塞控制（Congestion Control）

核心目标：避免网络拥塞（如路由器缓存溢出），通过调整发送方的发送速率，适配网络带宽；
核心算法：慢启动、拥塞避免、快速重传、快速恢复（详见后续问题）。

全双工通信（Full-Duplex）

核心定义：TCP 连接建立后，通信双方可同时发送和接收数据，无需等待对方发送完成；
实现基础：连接的两端各维护一个发送缓冲区和接收缓冲区，独立处理收发数据。

三、TCP 与 UDP 核心对比（表格）

特性	TCP	UDP
连接性	面向连接（三次握手）	无连接
可靠性	可靠（ACK、重传、校验和）	不可靠（无确认、无重传）
有序性	保证有序	不保证有序
数据边界	面向字节流（无边界）	面向数据报（有边界）
流量控制	支持（滑动窗口）	不支持
拥塞控制	支持	不支持
适用场景	文件传输、邮件、HTTP/HTTPS	视频直播、游戏、DNS、语音通话

四、面试加分点与记忆法

加分点

深度理解 "可靠传输" 的底层机制：ACK + 序列号是核心，重传和校验和是补充；
字节流与数据报的区别：解释 "粘包" 产生的原因（TCP 无边界）及解决方法；
工程应用：TCP 适合对可靠性要求高的场景（如文件传输），UDP 适合对实时性要求高的场景（如直播）。

记忆法推荐
核心特点记忆法："面向连接，可靠有序，字节流，流量拥塞双控制，全双工通信"；
TCP/UDP 对比记忆法："TCP 连、可靠、有序、控流量；UDP 无连、不可靠、无序、快传输"；
可靠性记忆法："ACK 确认，超时重传，序列号有序，校验和检错，滑动窗口控流量"。

请详细描述 TCP 三次握手的完整过程，并说明为什么需要三次握手？

一、TCP 三次握手的核心背景

TCP 是面向连接的协议，三次握手（Three-Way Handshake）是建立客户端与服务器之间 "可靠双向连接" 的过程，核心目标是同步双方的序列号和确认号，并交换 TCP 窗口大小等关键参数，保证连接的可靠性和双向通信能力。

二、三次握手的完整过程（基于客户端 - 服务器模型）

假设客户端为 C，服务器为 S，初始状态：C 的 TCP 处于 CLOSED 状态，S 的 TCP 处于 LISTEN 状态（监听端口）。

第一次握手：客户端 → 服务器（SYN 报文）

报文内容 ：
- 标志位：SYN（Synchronize）=1（表示请求建立连接）；
- 序列号（Seq）：随机生成的初始序列号，记为 ISN_C（如 x）；
- 窗口大小：客户端的接收窗口大小（告知服务器自己的接收能力）；
状态变化 ：
- 客户端：发送 SYN 后，从 CLOSED → SYN_SENT 状态；
- 服务器：收到 SYN 后，知晓客户端请求建立连接，记录客户端的 ISN_C=x。

第二次握手：服务器 → 客户端（SYN+ACK 报文）

报文内容 ：
- 标志位：SYN=1（服务器同步序列号） + ACK=1（确认客户端的 SYN）；
- 确认号（Ack）：x+1（表示期望接收客户端的下一个字节为 x+1，确认已收到 x）；
- 序列号（Seq）：服务器随机生成的初始序列号，记为 ISN_S（如 y）；
- 窗口大小：服务器的接收窗口大小；
状态变化 ：
- 服务器：发送 SYN+ACK 后，从 LISTEN → SYN_RCVD 状态；
- 客户端：收到 SYN+ACK 后，确认服务器已收到自己的连接请求，同时获取服务器的 ISN_S=y。

第三次握手：客户端 → 服务器（ACK 报文）

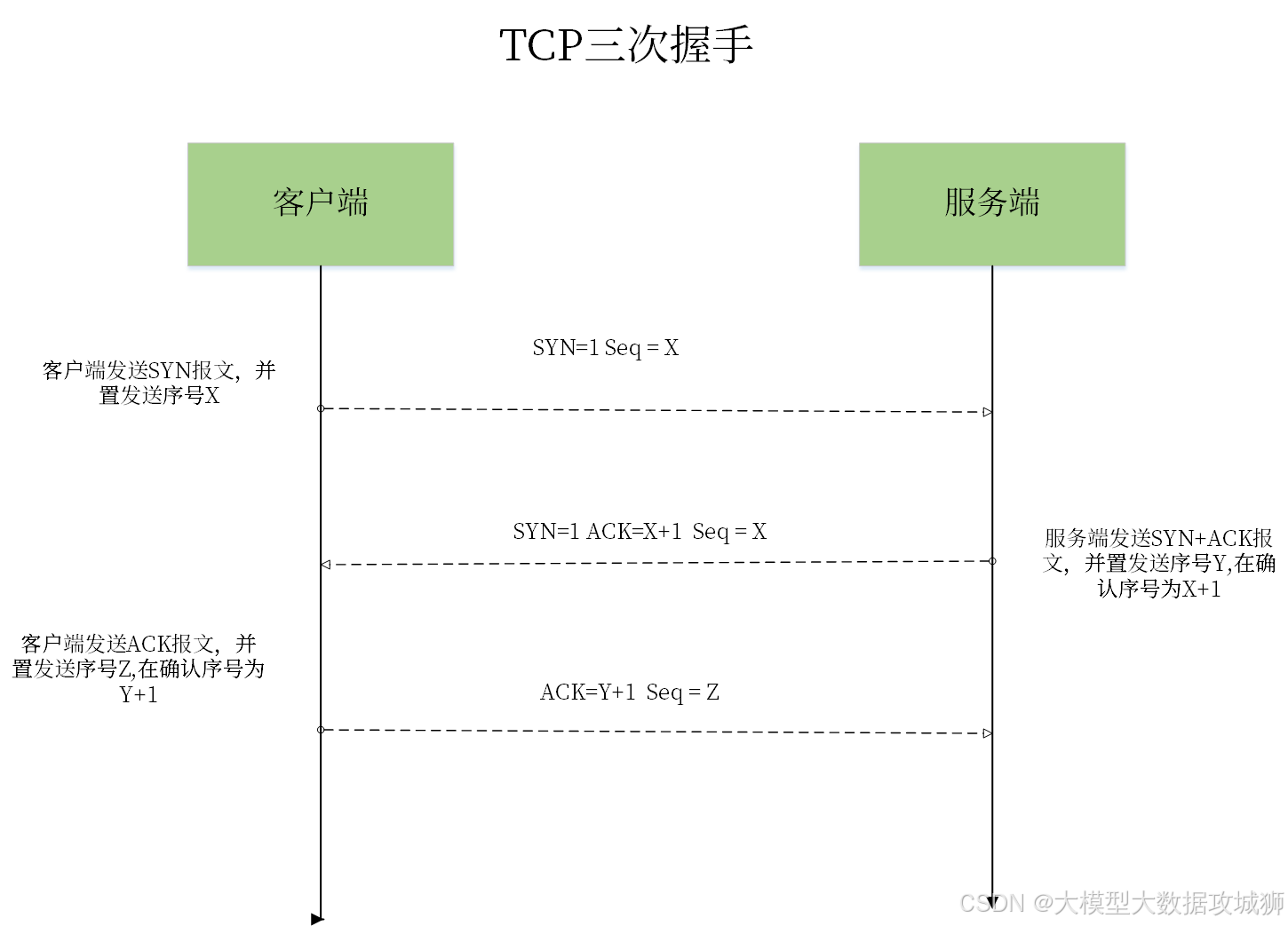
报文内容 ：
- 标志位：ACK=1（确认服务器的 SYN）；
- 确认号（Ack）：y+1（表示期望接收服务器的下一个字节为 y+1，确认已收到 y）；
- 序列号（Seq）：x+1（基于第一次握手的 ISN_C=x，递增 1）；
状态变化 ：
- 客户端：发送 ACK 后，从 SYN_SENT → ESTABLISHED 状态（连接建立，可收发数据）；
- 服务器：收到 ACK 后，从 SYN_RCVD → ESTABLISHED 状态（连接建立）。

三、为什么需要三次握手？（核心原因）

核心目标：同步双方的序列号，保证可靠双向通信

TCP 是全双工协议，双方需同时发送和接收数据，必须明确对方的初始序列号（ISN），才能通过序列号 / 确认号保证数据有序和可靠：

第一次握手：客户端告知服务器自己的 ISN（x），但服务器未确认收到；
第二次握手：服务器告知客户端自己的 ISN（y），并确认收到客户端的 ISN（x）；
第三次握手：客户端确认收到服务器的 ISN（y），服务器此时知晓客户端已获取自己的 ISN，双向序列号同步完成。

避免 "失效的连接请求" 导致的资源浪费

场景假设：若只有两次握手，客户端发送的 SYN 报文因网络延迟滞留，客户端超时后重发 SYN 并建立连接，通信完成后释放连接；此时滞留的旧 SYN 报文到达服务器，服务器发送 SYN+ACK（第二次握手），若没有第三次握手，服务器会认为连接已建立，分配资源等待客户端数据，但客户端已释放连接，导致服务器资源浪费；
三次握手的作用：服务器需收到客户端的第三次 ACK，才确认连接有效，旧 SYN 报文的第二次握手（SYN+ACK）会因客户端无响应（客户端已无对应连接）而超时，服务器释放资源，避免浪费。

验证双方的收发能力

第一次握手：服务器验证客户端的发送能力（能收到 SYN）；
第二次握手：客户端验证服务器的接收和发送能力（能收到 SYN 并发送 SYN+ACK）；
第三次握手：服务器验证客户端的接收能力（能收到 SYN+ACK 并发送 ACK）；
三次握手完成，双方确认彼此的收发能力正常，保证后续数据传输的可靠性。

四、关键细节与面试加分点

初始序列号（ISN）的生成规则

ISN 并非固定值，而是基于系统时钟和随机数生成，避免旧连接的报文段干扰新连接（如 ISN 重复导致序列号冲突）；
每建立一个新连接，ISN 递增（如每 4 微秒加 1），降低冲突概率。

半连接队列与全连接队列

服务器处于 SYN_RCVD 状态的连接会进入 "半连接队列"（SYN 队列）；
收到第三次 ACK 后，连接从半连接队列转入 "全连接队列"（Accept 队列），应用层通过 accept () 获取连接。

加分点

解释 "两次握手不可行" 的具体场景（失效 SYN 导致资源浪费），体现对协议设计的深度理解；
关联实际问题：SYN 泛洪攻击（攻击者发送大量 SYN 报文，占满半连接队列），防御手段（SYN Cookie）；
对比四次挥手：三次握手建立连接，四次挥手释放连接，核心差异是 "关闭连接需确认数据传输完成"。

五、记忆法推荐

三次握手过程记忆法："第一次 C 发 SYN（x），S 收；第二次 S 发 SYN（y）+ACK（x+1），C 收；第三次 C 发 ACK（y+1），S 收，双方 ESTABLISHED"；
三次握手原因记忆法："同步序列号，防失效请求，验收发能力，三次才可靠"；
核心目标记忆法："三次握手 = 双向序列号同步 + 双向收发能力验证"。

请详细叙述 TCP 拥塞控制的核心方法。

一、TCP 拥塞控制的核心背景

TCP 拥塞控制是指发送方根据网络拥塞状态调整发送速率的机制，核心目标是避免网络中出现过多报文段导致路由器缓存溢出、丢包、延迟增加，同时最大化利用网络带宽。拥塞控制与流量控制的区别：

流量控制：解决 "发送方与接收方的速率匹配"（端到端）；
拥塞控制：解决 "发送方与网络带宽的匹配"（全网级）。

TCP 拥塞控制的核心是维护一个 "拥塞窗口（Congestion Window，cwnd）"，发送方的实际发送窗口 = min (cwnd, 接收窗口)，cwnd 的大小决定了发送方一次可发送的最大报文段数。

二、TCP 拥塞控制的核心阶段（四大算法）

慢启动（Slow Start）

核心原理：连接建立初期，cwnd 从 1 开始指数增长，快速探测网络可用带宽，直到触发 "慢启动阈值（ssthresh）" 或检测到拥塞；
执行规则 ：
- 初始状态：cwnd=1（表示一次可发送 1 个报文段），ssthresh 为预设值（如 65535 字节）；
- 每收到一个 ACK，cwnd *= 2（指数增长）；
- 终止条件：
  - 若 cwnd ≥ ssthresh，进入 "拥塞避免" 阶段；
  - 若检测到拥塞（超时重传），则 ssthresh = cwnd/2，cwnd 重置为 1，重新慢启动。
示例：cwnd 初始 = 1 → 收到 ACK→2 → 收到 ACK→4 → 收到 ACK→8... 直到 cwnd=ssthresh。

拥塞避免（Congestion Avoidance）

核心原理：cwnd 超过 ssthresh 后，改为线性增长，缓慢增加发送速率，避免网络拥塞；
执行规则 ：
- 每收到一个 ACK，cwnd += 1（线性增长，而非指数）；
- 终止条件：
  - 检测到拥塞（超时重传）：ssthresh = cwnd/2，cwnd 重置为 1，重新慢启动；
  - 收到 3 个重复 ACK（快速重传触发）：进入 "快速恢复" 阶段。
核心目的：线性增长降低拥塞概率，平衡 "带宽利用" 与 "拥塞风险"。

快速重传（Fast Retransmit）

核心原理：避免超时重传的长等待时间，接收方收到乱序报文段时，连续发送 3 个重复 ACK，发送方立即重传缺失的报文段，无需等待定时器超时；
执行规则 ：
- 接收方：若收到报文段的序列号不是期望的，立即发送重复 ACK（确认号为期望的序列号）；
- 发送方：收到 3 个重复 ACK，判定为 "报文段丢失但网络未拥塞"，立即重传丢失的报文段，同时进入快速恢复阶段。

快速恢复（Fast Recovery）

核心原理：快速重传后，不重置 cwnd 为 1（避免慢启动的低效率），而是调整 cwnd 和 ssthresh，快速恢复发送速率；
执行规则（Reno 版本） ：
- 发送方收到 3 个重复 ACK 后：
  1. ssthresh = cwnd/2；
  2. cwnd = ssthresh + 3（补偿 3 个重复 ACK 对应的已接收报文段）；
- 后续每收到一个重复 ACK，cwnd += 1；
- 收到新的 ACK（确认丢失的报文段已接收），cwnd = ssthresh，进入拥塞避免阶段；
核心目的：在避免拥塞的前提下，快速恢复发送速率，减少带宽浪费。

三、拥塞检测的核心手段

TCP 通过以下方式检测网络拥塞：

超时重传：发送方定时器超时未收到 ACK，判定为严重拥塞（报文段丢失，网络缓存溢出）；
重复 ACK：连续 3 个重复 ACK，判定为报文段丢失但网络未拥塞（乱序导致，非缓存溢出）；
延迟增加：通过 RTT（往返时间）变化辅助判断，RTT 骤增可能预示拥塞。

四、TCP 拥塞控制的演进（面试加分）

Reno 版本（经典版本）

核心：慢启动 + 拥塞避免 + 快速重传 + 快速恢复，解决了基本的拥塞问题，但存在 "多包丢失" 时效率低的问题。

NewReno 版本

优化：支持多包丢失的快速恢复，无需多次慢启动，提升多包丢失场景的效率。

CUBIC 版本（Linux 默认）

核心：基于立方函数的拥塞窗口增长，高带宽延迟积（BDP）网络下更高效，避免 Reno 的线性增长在高速网络中效率低的问题。

BBR 版本（ogle 提出）

核心：基于带宽和延迟的模型，不再依赖丢包检测拥塞，适合高带宽、高延迟的网络（如 5G、卫星通信）。

五、关键细节与面试加分点

拥塞窗口与接收窗口的关系

发送方实际发送窗口 = min (cwnd, rwnd)，其中 rwnd 为接收方的接收窗口；
若 rwnd < cwnd：受流量控制限制，发送速率由接收方决定；
若 cwnd < rwnd：受拥塞控制限制，发送速率由网络带宽决定。

加分点

区分拥塞控制与流量控制：前者针对网络，后者针对接收方；
解释慢启动的 "慢"：并非速率慢，而是初始值小，指数增长实际很快，"慢" 是相对直接满速发送；
工程应用：不同场景选择不同拥塞控制算法（如短视频用 BBR，传统网络用 CUBIC）。

六、记忆法推荐

核心阶段记忆法："慢启动指数涨，到阈值线性涨（拥塞避免），3 个重复 ACK 快重传，快恢复不重置 cwnd"；
cwnd 变化记忆法："拥塞（超时）：ssthresh=cwnd/2，cwnd=1；快恢复：ssthresh=cwnd/2，cwnd=ssthresh+3，恢复后拥塞避免"；
核心目标记忆法："拥塞控制 = 探带宽（慢启动）+ 稳速率（拥塞避免）+ 快恢复（少丢包），平衡带宽利用与拥塞风险"。