【论文学习】通过编辑习得分数函数实现扩散模型中的图像隐藏

Hiding Images in Diffusion Models by Editing Learned Score Functions

通过编辑习得分数函数实现扩散模型中的图像隐藏

一种在扩散模型中隐藏秘密图像的技术 ，通过修改模型训练后学到的 "分数函数"，在反向去噪的特定步骤嵌入秘密图像，既不影响模型正常生成图像的功能，又能让授权者用密钥精准提取秘密图像。

扩散模型：一种能生成高质量图像的 AI 模型，工作流程分两步：

1. 前向过程：给清晰图像逐步加噪声，直到变成完全随机的噪声；
2. 反向过程：模型从随机噪声开始，一步步 "去噪"，最终还原出清晰图像

习得分数函数：扩散模型训练后学到的核心工具，本质是 "噪声估计函数"。它能判断某张带噪图像里的噪声类型和强度，是反向去噪过程的 "核心算法"

图像隐藏：属于 "隐写术"，不是把秘密图像存在文件里，而是嵌入到 AI 模型本身 ------ 模型看起来还能正常生成图像，但只有知道密钥的人，才能从模型里提取出隐藏的秘密图像。

不是修改整个模型，而是精准 "微调" 分数函数的局部，步骤很简单：

1. 选一个 "秘密时间步"：在反向去噪的众多步骤中，挑一个特定步骤（比如第 500 步）作为隐藏点；
2. 编辑分数函数：在这个时间步里，给分数函数插入 "秘密映射"------ 用密钥生成特定噪声，让分数函数在处理这种噪声时，自动关联到要隐藏的秘密图像；
3. 保持模型正常功能：编辑只针对单个时间步，不干扰其他去噪步骤，所以模型对外表现和原来一样，能正常生成图像，不会被察觉。

之前的扩散模型隐写方法，要么藏得不清楚、要么模型生成质量变差、要么速度慢，而这种方法的优势的核心就是 "精准编辑"：

1. 提取准：只在一个时间步嵌入，秘密图像不会被其他去噪步骤干扰，提取时用密钥定位到这个时间步，就能还原高清图像
2. 不影响模型：只改分数函数的局部，模型生成图像的质量几乎和原来一致
3. 速度快：不用重新训练整个模型，只微调少量参数

摘要

利用神经网络隐藏数据（即神经隐写术）已在判别式分类器和生成对抗网络（GANs）中取得了显著成功。然而，扩散模型中的数据隐藏潜力尚未得到充分探索。现有方法在实现高提取精度、模型保真度和隐藏效率方面存在局限，这主要是由于隐藏与提取过程与多个去噪扩散步骤相互纠缠所致。为解决这些问题，我们提出一种简单而有效的方法：通过编辑习得分数函数，在反向扩散过程的特定时间步嵌入图像。此外，我们引入一种参数高效微调（PEFT）方法，结合基于梯度的参数选择与低秩适配（LoRA），以提升模型保真度与隐藏效率。综合实验表明，该方法提取出的高质量图像达到人眼无法区分的水平，在样本级和总体级上均能复刻原始模型的行为，且图像嵌入速度较以往方法快一个数量级。此外，该方法通过独立的提取通道，天然支持多接收者场景。

理解1

利用神经网络隐藏数据（即神经隐写术）已在判别式分类器和生成对抗网络（GANs）中取得了显著成功。

神经隐写术 ：把秘密数据藏在神经网络里而非传统文件中

神经隐写术已经在两类主流 AI 模型（判别式分类器、GANs）里成熟应用，既能藏得隐蔽，又能精准提取，还不影响模型本身的正常功能。

神经隐写术和传统 "把秘密文件藏在图片像素里" 的隐写术不一样，神经隐写术是把秘密数据（比如秘密图像、文字）直接嵌入到 AI 模型的参数或结构里。

1. 模型表面上还能正常干活（比如识别图片、生成图片），外人完全看不出异常；
2. 只有知道密钥的授权者，才能从模型里把秘密数据提取出来，安全性更高。

两类 "藏数据成功" 的 AI 模型：

判别式分类器：藏在 "判断型 AI" 里

1. 这类模型的核心功能是 "做分类 / 判断"：比如识别一张图片是猫还是狗、判断邮件是不是垃圾邮件、检测照片里的人脸。
2. 怎么藏数据？：悄悄修改模型里的少量关键参数（比如调整某些权重的微小数值），把秘密数据 "编码" 进去。
3. 成功的表现：模型还是能精准分类（比如识别猫的准确率没下降），但授权者用密钥就能从这些参数里还原出秘密数据，不会被外人发现。

生成对抗网络（GANs）：藏在 "创作型 AI" 里

1. 这类模型的核心功能是 "生成新数据"：比如生成逼真的人脸、风景图、手写文字，甚至模仿特定风格的图片。
2. 怎么藏数据？：要么在模型生成的图像里 "悄悄植入秘密信息"（比如生成的风景图里，像素细节藏着文字密码），要么直接把完整的秘密图像嵌在模型的生成逻辑里。
3. 成功的表现：生成的图像依然逼真（和没藏数据的 GAN 生成效果一样），授权者能通过特定方法（比如输入密钥）从生成结果或模型本身，精准提取出隐藏的秘密数据。

"显著成功" 的关键体现

1. 隐蔽性强：模型正常功能不受影响（分类准、生成真），传统检测工具找不到藏的数据；
2. 提取精准：藏进去的秘密（比如一张完整图像），提取出来后几乎没失真，能正常使用；
3. 抗干扰：模型经过轻微调整（比如微调优化）后，藏的数据依然能稳定提取，不会丢失。

理解2

然而，扩散模型中的数据隐藏潜力尚未得到充分探索。现有方法在实现高提取精度、模型保真度和隐藏效率方面存在局限，这主要是由于隐藏与提取过程与多个去噪扩散步骤相互纠缠所致。

扩散模型本是数据隐藏的好载体，但目前相关技术还没成熟；现有方法之所以做不到 "藏得准、模型不失效、藏得快"，根源是把 "藏 / 取数据" 和扩散模型的 "多步去噪" 绑在了一起，互相干扰拖了后腿。

扩散模型的数据隐藏潜力未充分探索：

扩散模型（另一种更先进的生成式 AI，靠 "逐步去噪" 生成高清图像）的相关应用还很欠缺，它生成图像的过程本身有天然的隐藏优势（比如步骤多、参数复杂，适合藏信息），但目前还没人找到高效利用这些优势的方法

现有方法想在扩散模型里藏数据，却达不到三个关键要求：

1. 高提取精度：藏进去的秘密图像（比如一张照片），取出来后得清晰、没失真（比如 PSNR 值高，肉眼看不出差异）；
2. 模型保真度：藏了数据后，扩散模型本身还得正常干活 ------ 生成的图像质量和没藏数据时差不多（比如 FID 值接近原始模型），不能一看就知道 "这模型被动过手脚"；
3. 隐藏效率：藏数据的过程不能太费时间（比如不用花十几个 GPU 小时），得高效快捷。

关键原因："隐藏 / 提取过程与多个去噪扩散步骤相互纠缠"

理解3

为解决这些问题，我们提出一种简单而有效的方法：通过编辑习得分数函数，在反向扩散过程的特定时间步嵌入图像。

针对现有方法 "藏数据和去噪步骤纠缠" 的问题，提出一套 "精准定点" 的解决方案 ------ 只在反向扩散的某一个特定步骤，悄悄修改模型的习得分数函数，把秘密图像嵌进去，既不打乱整体去噪流程，又能高效精准提取。

特定时间步：只选 "一个打磨步骤" 做文章

编辑习得分数函数：给 "去噪导航仪" 加个 "秘密指令"

习得分数函数是模型的 "去噪导航仪"，负责判断每一步该怎么去噪才能生成清晰图像。

• 编辑的核心不是换掉导航仪，而是给它加个 "条件指令"：当走到约定的 "秘密时间步 tₛ"，且遇到用密钥生成的 "特定噪声 zₛ" 时，就自动把秘密图像的信息嵌入进去；
• 这个编辑是 "局部微调"：只改导航仪在 "秘密时间步" 处理 "特定噪声" 的逻辑，其他时候导航仪还按原来的规则工作，不影响模型正常生成图像。

具体流程：

藏图像（sender 操作）

1. 选秘密密钥 Kₛ：包含 "噪声种子 kₛ" 和 "秘密时间步 tₛ"；
2. 用 kₛ生成特定高斯噪声 zₛ；
3. 编辑分数函数：让它在 "tₛ步" 处理 "zₛ噪声" 时，关联要隐藏的秘密图像 xₛ；
4. 用混合 PEFT 策略微调模型：只调整和这个编辑相关的少量参数（减少 86.3% 可训练参数），不用重训整个模型；
5. 公开分享修改后的模型：外人看起来它和原模型没区别，生成图像质量一样。

取图像（recipient 操作）

1. 拿到 sender 私下分享的密钥 Kₛ（知道 tₛ和 kₛ）；
2. 用 kₛ生成同样的噪声 zₛ，输入公开的模型；
3. 让模型在 "tₛ步" 处理 zₛ：因为分数函数有之前的 "秘密指令"，会直接输出隐藏的秘密图像 xₛ，一步就能提取，不用走完整去噪流程。

理解4

此外，我们引入一种参数高效微调（PEFT）方法，结合基于梯度的参数选择与低秩适配（LoRA），以提升模型保真度与隐藏效率。

为了让藏过图像的模型依然 "好用"（高保真度）、藏图像的过程更快（高效率），我们设计了一套 "精准且省力" 的微调方案 ，先挑出对 "藏图像" 最关键的模型参数，再用一种轻量的低秩适配技术微调这些参数，不用改动整个模型，就能兼顾效果和速度。

之前的方法（包括传统微调）有个痛点：想藏图像，要么 "大改模型"（全量微调）------ 虽然可能藏得准，但模型容易 "变味"（生成的图像质量下降，保真度差），还特别费时间；要么 "小改模型"------ 虽然模型不变味，但藏得不准、效率也一般。

PEFT 的核心就是 "只改该改的，不改多余的"：不用重新训练整个模型，只针对性调整少量关键参数，既不破坏模型原有功能，又能高效完成 "藏图像" 的任务。

基于梯度的参数选择：找出 "最该改的零件"

"梯度"能判断每个参数对 "藏图像" 任务的重要性 ------ 参数的梯度越大，说明改它对藏图像的效果影响越明显（比如有的参数改一点点，秘密图像的提取精度就大幅提升；有的参数改了也没用）。

操作逻辑：计算每个参数的梯度，筛选出梯度最大的 "关键参数"

低秩适配（LoRA）：轻量改造 "关键零件"，不破坏原有功能

选出关键参数后，不是直接修改这些参数的原始值（容易改乱模型），而是用 LoRA 技术做 "轻量补充"：

1. LoRA 的本质：给关键参数 "加个小插件"，而不是 "换零件"。具体来说，就是在模型的关键层（比如之前选的敏感层）里，插入两个很小的 "低秩矩阵"（可以理解为两个简单的计算模块），藏图像的逻辑就通过这两个小模块实现。
2. 核心优势：
   1. 轻量化：这两个小矩阵的参数数量远少于原模型参数（论文中减少了 86.3% 的可训练参数），微调起来特别快，大大提升隐藏效率；
   2. 保保真度：原模型的核心参数没动，只是加了 "补充模块"，所以模型生成图像的功能几乎不受影响，和没藏过图像的原模型表现一致。

引言

数据隐藏技术的发展与数字媒体的进步相伴相生，已从传统的比特流操作 [8] 逐步演进至深度学习范式 [1, 3, 60]。神经网络隐藏数据的主流方案采用自编码器架构：编码网络将秘密信息嵌入某种载体媒体，解码网络则负责提取该信息。尽管该方案的可行性已得到验证，但其实际部署仍面临三大核心局限：首先，解码网络的安全传输需求会带来后勤漏洞 [10, 11]；其次，最先进的隐写分析工具 [4, 12, 18, 19, 33, 52, 57] 能从载体媒体（通常为数字图像和视频）中高精度检测出嵌入信息，导致保密性受损；最后，多接收者场景需要复杂的密钥设计与管理 [3, 25, 53, 55, 65]。

一种新的范式应运而生 ------ 将数据隐藏于神经网络之中 [5, 32, 44, 50, 51]，即秘密数据直接嵌入模型参数。该方法可规避传统隐写分析工具的检测，因为这类工具的设计目标是分析隐写载体媒体，而非神经网络权重。起初，此类隐藏方法在判别模型中取得了成功 [32, 44, 50, 51]。然而，近年来随着生成模型的实用性提升与应用普及，研究焦点已转向这一领域。此外，生成模型无需单独的解码网络即可直接生成秘密数据，从根本上解决了传输安全问题。例如，Chen 等人 [5] 提出在深度生成模型习得的分布特定位置嵌入图像，该方法在生成对抗网络（GANs）[14] 的变体 SinGANs [41] 中已被证实有效。

扩散模型 [21, 47] 的出现为这种生成式概率隐藏方法带来了新的机遇。尽管部分现有方法 [6, 7, 36] 的用途略有不同（如后门攻击或水印），但它们仍面临关键瓶颈（见表 1）：首先，这些方法难以隐藏结构和纹理丰富的复杂自然图像，重建峰值信噪比（PSNR）≤25 dB；其次，模型保真度受损严重，弗雷歇初始距离（FID）[20] 退化超过 100%，存在被检测的风险；最后，它们需要对模型进行全量重训练或微调（≥10 GPU 小时），以学习并行的秘密扩散过程。

本文提出一种简单而有效的扩散模型图像隐藏方法。我们发现，在反向扩散过程的特定时间步，通过编辑习得分数函数（插入密钥 - 图像映射关系），可实现精准的图像嵌入，且不会破坏反向扩散的原始流程。隐写扩散模型可公开共享 ¹，其生成分布内高质量图像的行为与原始模型一致。秘密图像的提取通过密钥引导且时间步条件约束的 "去噪" 一步完成。为进一步提升模型保真度与隐藏效率，我们引入一种混合参数高效微调（PEFT）方法，结合基于梯度的参数选择 [15] 与低秩适配（LoRA）[23]，与全量微调相比，可减少 86.3% 的可训练参数。综合实验表明，该方法在四个关键维度均表现优异：1）提取精度 ------32×32 图像的峰值信噪比（PSNR）达 52.90 dB，256×256 图像达 39.33 dB；2）模型保真度 ------ 保持近乎原始的 FID 分数（在 CIFAR10 [28] 数据集上为 4.77，原始模型为 4.79），样本级失真极小；3）隐藏效率 ------32×32 和 256×256 图像的嵌入时间分别降至 0.04 和 0.18 GPU 小时；4）扩展性 ------ 通过独立提取密钥，可同时为不同接收者嵌入四张图像。

理解1

神经网络隐藏数据的主流方案采用自编码器架构：编码网络将秘密信息嵌入某种载体媒体，解码网络则负责提取该信息。尽管该方案的可行性已得到验证，但其实际部署仍面临三大核心局限：首先，解码网络的安全传输需求会带来后勤漏洞 [10, 11]；其次，最先进的隐写分析工具 [4, 12, 18, 19, 33, 52, 57] 能从载体媒体（通常为数字图像和视频）中高精度检测出嵌入信息，导致保密性受损；最后，多接收者场景需要复杂的密钥设计与管理 [3, 25, 53, 55, 65]。

用自编码器做神经隐写术（藏秘密数据）的思路 ：编码网络把秘密嵌进载体 ，解码网络负责提取，但实际用的时候会遇到三个绕不开的问题，导致不好落地。

自编码器架构：

1. 编码网络（加密端）：相当于 "隐形笔"，把秘密信息（比如一张秘密照片、一段文字）嵌入到 "载体媒体" 里 ------ 载体就是日常能看到的数字图像、视频（比如一张风景照、一段短视频），嵌入后载体看起来和原来没区别，外人看不出异常。
2. 解码网络（解密端）：相当于 "解密眼镜"，只有用它才能从载体里把秘密信息提取出来，没有这个工具，就算拿到载体也找不到秘密。

三大核心局限：

1. 解码网络的安全传输会带来 "后勤漏洞"：想让 recipient 提取秘密，必须把 "解密眼镜"（解码网络）安全传给对方，但这步很容易出问题：
   • 传输风险：解码网络是软件 / 模型文件，传输过程中可能被拦截、篡改 ------ 如果被第三方拿到，对方就能用它提取载体里的秘密，保密性直接失效；
   • 后勤麻烦：如果要更新解码网络（比如提升安全性），得重新给所有 recipient 传新版本，还得确保旧版本被销毁，管理成本高，容易出现疏漏（比如有人没更旧版本，导致秘密泄露）
2. 先进的 "隐写分析工具" 能精准查出秘密，保密性作废：

• "专门找隐形字的探测器"，现在的技术已经很成熟了：
  • 它不关心 "解密眼镜" 是什么，直接分析载体本身（比如那张风景照）------ 通过检测图像的像素细节、纹理变化、统计特征，就能判断这张图里是不是藏了秘密；
  • 结果：就算编码网络藏得再隐蔽，只要载体经过这些 "探测器"，秘密就会被发现，相当于 "隐形字被看穿"，根本达不到隐藏的目的。

1. 多接收者场景下，密钥设计和管理太复杂

• recipient 传不同秘密（比如给 A 传秘密照片、给 B 传秘密文字），这套方案就绕不开 "密钥麻烦"：
  • 得给每个 recipient 设计专属密钥（比如不同的 "解密眼镜参数"），还要确保 A 的密钥解不开 B 的秘密，避免混淆；
  • 管理成本高：要记录每个 recipient 的密钥，还要定期更新密钥（提升安全性），一旦密钥丢失、被盗，对应的秘密就会泄露，而且很难追溯。

理解2

一种新的范式应运而生 ------ 将数据隐藏于神经网络之中 [5, 32, 44, 50, 51]，即秘密数据直接嵌入模型参数。该方法可规避传统隐写分析工具的检测，因为这类工具的设计目标是分析隐写载体媒体，而非神经网络权重。

出现了一种全新的隐写思路 ------ 不把秘密数据藏在图片、视频这些 "载体媒体" 里，而是直接嵌进神经网络的 "模型参数"（相当于模型的核心规则 / 记忆）里。这种操作能躲开传统检测工具的排查，因为那些工具本来就只盯着载体媒体找异常，根本不会去分析神经网络的内部权重。

之前的隐写术（比如自编码器方案）是 "借载体藏东西"

神经网络的 "模型参数"，就是模型里成千上万的权重、偏置数值。

1. 嵌入操作：悄悄微调这些参数里的少量关键数值，把秘密数据（比如图像的像素信息、文字的编码）"编码" 进去 ------ 比如把某几个权重的小数位调整为特定数值，组合起来就是秘密信息；
2. 模型功能不受影响：微调的幅度极小，且只改关键参数，模型依然能正常干活（比如判别模型继续分类、生成模型继续生成图像），外人完全看不出模型被动过手脚。

传统隐写分析工具的 "工作目标" 是固定的 ------ 只分析 "载体媒体" 的异常：

1. 比如检测图片的像素统计特征（比如某类颜色的像素突然变多）、视频的帧间差异，本质是 "在载体上找修改痕迹"；
2. 但新范式里，秘密数据根本不在载体上，而是在神经网络的内部参数（权重）里。这些工具不会去读取、分析模型的内部权重数值，自然就找不到任何异常，相当于 "探测器盯着书本找纸条，却不知道纸条已经变成了排版规则"。

相关工作

神经隐写术

本文主要聚焦于神经网络中的数据隐藏技术 [5, 32, 44, 50, 51]，该技术将秘密数据嵌入神经网络的参数或结构中，在不影响模型性能的前提下实现隐蔽通信。代表性的神经隐写术策略包括：替换模型参数的最低有效位 [32, 44]、替换冗余参数 [32, 51]、将参数值 [32, 44, 50] 或符号 [32, 44] 直接映射为秘密信息、记忆带有秘密标签的合成数据 [44]，以及在深度概率模型中隐藏图像 [5]。尽管这些方法已被证实有效，但扩散模型在神经隐写术领域尚未得到充分探索。

扩散模型

扩散模型是生成式建模领域的一项重要突破，通过多步去噪扩散过程实现高质量数据合成。该模型受非平衡热力学 [43] 和经验贝叶斯中的分数匹配 [24, 38] 启发，定义了前向扩散过程和反向（生成）扩散过程：前向过程逐步向数据中添加噪声直至其变为随机噪声，反向过程则学习迭代去除噪声以重建原始数据。与生成对抗网络（GANs）不同，扩散模型优化基于似然的目标函数 [21, 46]，通常能实现更稳定的训练和更全面的模式覆盖。在架构上，扩散模型主要采用 U-Net [40] 和 Transformer [48]，可在像素空间 [21, 27, 47] 或 latent 空间 [35, 37, 39] 中运行。

现有扩散模型数据隐藏方法通常需要同时训练秘密反向扩散过程 [6, 7, 36]，导致其存在提取精度有限、模型保真度显著下降以及计算成本高昂等问题，尤其在处理复杂自然图像时表现突出。扩散模型编辑技术 [13, 29, 54, 56] 最初用于修改或移除已学习的概念和规则，部分技术已被适配用于嵌入不可见但可恢复的水印信号 [10, 11]。然而，这些编辑技术无法满足本文所需的精准图像重建要求。

参数高效微调

参数高效微调（PEFT）方法大致可分为两类：选择性微调与重参数化微调。选择性微调基于简单启发式规则 [59] 或参数梯度 [17, 63]，策略性地筛选部分参数进行调整；重参数化微调则在预训练冻结骨干网络中引入额外的可训练参数，典型示例包括提示微调 [30]、适配器 [22]、低秩适配（LoRA）[23] 及其变体 [16, 26, 34, 61]。本文提出一种混合 PEFT 方法，用于像素空间扩散模型的图像隐藏，有效融合了选择性微调与重参数化微调的优势。

扩散模型中的图像隐藏

本节首先介绍扩散模型的必要基础知识，为所提方法奠定理论基础。随后，我们描述典型的图像隐藏场景，并详细阐述基于扩散模型的隐写术方法（见图 1）。

图一

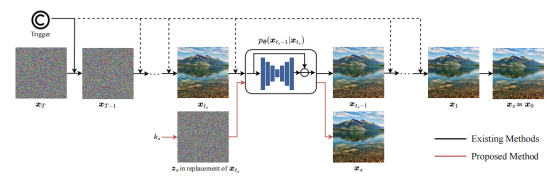
现有方法通常在反向扩散过程的初始时间步嵌入触发模式（作为秘密密钥），并可在后续所有时间步持续嵌入（用虚线表示）。这些模式引导秘密图像x**s 的重建，但由于对整个反向扩散过程的持续干预，会损害模型保真度并降低隐藏效率。与之形成鲜明对比的是，所提方法采用选择性操作：秘密图像x**s 仅在私下选定的时间步t**s 进行嵌入和提取。隐藏过程由秘密密钥k**s 控制，该密钥作为生成输入高斯噪声z**s的种子。通过将干预局限于单个时间步，反向扩散过程的完整性得以保留。

基础知识

扩散模型（尤其是去噪扩散概率模型，DDPMs [21]）是近年来涌现的最先进深度生成模型，能够通过定义的扩散过程合成高质量图像。

前向扩散过程

反向扩散过程

图像隐藏场景

我们参考 Simmons [42] 提出的经典 "囚徒问题" 框架，考虑单图像隐藏场景，涉及三方主体：

• 发送方：使用秘密密钥(K_s)将秘密图像(x_s)嵌入扩散模型，并公开分享隐写扩散模型；
• 接收方：利用私下共享的秘密密钥(K_s)，从公开传输的隐写扩散模型中提取秘密图像(x_s)；
• 审查方：检查公开可用的扩散模型，验证其是否保留正常生成功能，且无异常行为。

该场景的核心目标有二：一是确保授权接收方能够高精度提取秘密图像；二是保证扩散模型在图像生成时的样本级和总体级保真度，使其在审查方的核查中不被察觉。

所提方法

核心思想

现有基于扩散模型的技术 [6, 7, 36] 通常通过修改反向扩散过程的整个马尔可夫链来嵌入秘密图像，导致在提取精度、模型保真度和隐藏效率方面面临严峻挑战。为解决这些问题，我们提出一种简单有效的隐藏方法，仅在单个时间步操作。该过程使用秘密密钥(K_s = {k_s, t_s})，其中(k_s)是确定性生成高斯噪声(z_s)的种子，(t_s)是选定的图像隐藏时间步。发送方与接收方私下传递秘密密钥(K_s)，实现秘密图像(x_s)精准、安全且快速的单步重建（其中(\bar{\theta})表示编辑后的最优参数）。

损失函数

多图像隐藏

基于 PEFT 的分数函数编辑

为同时提升模型保真度和隐藏效率，我们提出一种混合 PEFT 技术，融合选择性微调与重参数化微调的优势。该方法包括三个步骤：1）计算参数相对于编辑损失函数（公式 (9)）的敏感度；2）识别最敏感层；3）对选定层执行重参数化微调。

参数敏感度计算

敏感层选择

基于 LoRA 的微调

实验

本节首先介绍实验设置，随后从提取精度、模型保真度和隐藏效率三个关键维度，与九种主流神经隐写术方法进行全面对比，最后将分析扩展至多图像隐藏场景，验证所提方法的扩展性。

实验设置

实现细节

本文采用预训练去噪扩散概率模型（DDPMs）[21] 作为默认像素空间扩散模型，针对两种图像分辨率开展实验：基于 CIFAR10 数据集 [28] 的 32×32 像素图像，以及基于 LSUN 卧室数据集 [58] 的 256×256 像素图像。与以往方法 [6, 7, 36] 通常嵌入二维码、图标等过于简单的图像模式不同，本文采用来自 COCO [31]、DIV2K [2]、LSUN 教堂 [58] 和 Places [64] 等常用数据集的复杂自然图像评估方法性能。

DDPM 模型的架构与超参数遵循 [21] 中的设定。默认情况下，秘密图像的嵌入与提取均在时间步(t_s=500)进行。参数敏感性分析中，梯度累积迭代次数(N=50)；公式 (12) 中的阈值(\tau)根据图像分辨率调整，32×32 图像的敏感参数稀疏度设为 0.01，256×256 图像设为 0.1；对应地，敏感层数量(\eta)分别设为 15 和 45。LoRA 微调的最大迭代次数为 2000，32×32 图像的低秩矩阵秩(r=64)，256×256 图像的秩(r=128)。

评估指标

评估涵盖三个方面：1）提取精度，通过原始与提取秘密图像间的峰值信噪比（PSNR）、结构相似性（SSIM）指数 [49]、感知图像块相似度（LPIPS）[62] 和深度图像结构纹理相似度（DISTS）[9] 量化；2）模型保真度，样本级采用 PSNR、SSIM、LPIPS 和 DISTS 评估，总体级采用弗雷歇初始距离（FID）[20] 衡量原始模型与隐写模型生成图像的分布差异；3）隐藏效率，以在 AMD EPYC 7F52 16 核 CPU 和 NVIDIA GeForce RTX3090 GPU 上嵌入单张秘密图像所需的 GPU 小时数衡量。

主要结果

本文将所提方法与九种主流方法对比：五种自编码器类算法（Baluja17 [3]、HiDDeN [65]、Weng19 [53]、HiNet [25]、PRIS [55]）、一种 GAN 类方法（Chen22 [5]）以及三种扩散模型类方法（BadDiffusion [7]、TrojDiff [6]、WDM [36]）。

提取精度

由表 2 可知，自编码器类方法 [3, 25, 53, 55, 65] 在高分辨率图像上提取精度更高，而现有 GAN 类 [5] 和扩散模型类 [6, 7, 36] 方法在低分辨率图像上表现更优。所提方法在两种分辨率下均优于所有现有神经隐写术方法：32×32 图像的 PSNR 达 52.90 dB，256×256 图像达 39.33 dB。图 2 展示了 256×256 分辨率下原始秘密图像与提取图像的绝对误差图定性对比，视觉结果表明所提方法在所有空间位置的重建误差最小。

模型保真度

表 3 显示，所提方法的模型保真度最接近原始 DDPM 模型：32×32 图像的 FID 为 4.77（原始模型为 4.79），256×256 图像的 FID 为 8.39（原始模型为 7.46），FID 变化极小。样本级保真度指标（PSNR、SSIM、LPIPS、DISTS）也验证了所提方法生成的图像与原始模型视觉无差异。图 3 对比了相同初始噪声下原始模型与不同隐写模型生成的 256×256 图像，可见所提方法生成的图像与原始模型高度相似，而其他隐写模型在物体结构细节和背景颜色表现上存在明显差异。

隐藏效率

如表 3 所示，所提方法显著降低了嵌入时间：32×32 图像仅需 0.04 GPU 小时，256×256 图像仅需 0.18 GPU 小时，比次优方法 WDM [36] 快 50 倍以上。效率提升的核心原因是所提方法仅在私下选定的单个时间步(t_s)嵌入秘密图像，而非对整个反向扩散过程进行多轮迭代微调。

多图像隐藏

为验证扩展性，进一步评估多接收者多图像隐藏场景。表 4 表明，尽管嵌入更多图像会导致模型保真度略有下降，但所提方法仍能保持高提取精度，支持多接收者间的安全通信。

综上，综合实验证实所提方法实现了卓越的提取精度、高模型保真度和极高的隐藏效率，为扩散模型神经隐写术建立了新基准。

消融实验

为系统分析所提方法关键组件的贡献，在 32×32 图像上开展全面消融实验。

参数敏感性累积

首先评估公式 (11) 中敏感性累积迭代次数N对性能的影响。由表 5 可知，当N从 1 增加到 50 时，提取精度和模型保真度均显著提升；但进一步增加N至 100 时，性能提升微乎其微，却会带来额外计算开销。因此，选择(N=50)作为性能与计算效率的平衡方案。

敏感层选择数量

分析不同敏感层数量对性能的影响。表 6 显示，选择过少的层（如 5 层）会导致提取精度不足（PSNR 为 47.48 dB），尽管模型保真度良好；选择过多的层（如 45 层）会因参数调整过度降低模型保真度；平衡选择 15 层可在不损害模型保真度的前提下显著提升提取精度（PSNR 达 52.90 dB），因此将 15 层设为默认值。

秘密时间步选择

所提方法支持灵活选择秘密嵌入时间步(t_s)。图 4 展示了不同(t_s)对性能的影响，结果表明在广泛的时间步范围内，提取精度和模型保真度均保持稳定鲁棒，凸显了所提方法在多图像、多接收者等实际场景中的实用性和可靠性。

PEFT 迭代次数

探索 PEFT 迭代次数对性能的影响。表 7 显示，增加迭代次数通常会提升提取精度，但会降低模型保真度并大幅增加计算成本。例如，迭代次数较少时（如 1000 次），模型保真度较高但提取精度不足。因此，选择 2000 次迭代作为默认配置，以平衡提取精度、模型保真度和隐藏效率。

PEFT 与全量微调对比

对比所提 PEFT 策略与全量微调的效果和效率。表 8 清晰表明，所提 PEFT 方法在保持模型保真度方面显著优于全量微调，且仅需牺牲少量提取精度，计算时间减少一半（仅为全量微调的 50%）。

对图像噪声的鲁棒性

为评估对输入噪声的鲁棒性，在嵌入前对秘密自然图像添加随机高斯噪声（均值为 0，方差为 100）。表 8 证实了所提方法的抗干扰能力：在强噪声条件下，性能仅轻微下降，验证了其在加密传输环境中的潜在适用性。

跨扩散模型变体的兼容性

在多种主流扩散模型变体（DDPM [21]、DDPM++[47]、DDIM [45]、EDM [27]）上验证方法的适应性。表 9 显示，所提方法在这些不同扩散模型架构上均保持高提取精度和模型保真度，凸显了其广泛的泛化性和通用性。需注意，DDIM 推理时可能跳过部分去噪步骤，若恰好跳过选定的秘密时间步，会带来最优的模型保真度。

综上，消融实验充分验证了所提方法的效率、鲁棒性和适应性，证实其在神经隐写术应用中的实际有效性。

结论与讨论

本文提出了一种通过混合参数高效微调（PEFT）策略，在特定时间步编辑习得分数函数，从而在扩散模型中隐藏图像的计算方法。与现有方法相比，该方法实现了卓越的提取精度，保持了模型保真度，并显著提升了隐藏效率。通过大量实验与严格的消融研究，我们明确了驱动方法优越性能的关键因素 ------ 局部化的分数函数编辑被证实是一项重要贡献，其能够以极低的计算成本实现精准调整。

展望未来，本研究衍生出多个极具前景的研究方向。其中一个核心方向是开发自适应隐藏策略，该策略可根据数据特征或安全需求动态调整嵌入参数。此外，对不同嵌入场景下扩散模型的行为进行严谨的理论分析（包括可检测性的理论上界），对于充分挖掘和理解基于扩散模型的神经隐写术潜力至关重要。最后，提升嵌入过程对模型扰动（如噪声干扰、模型剪枝与压缩）的鲁棒性，有望将该方法转化为高效的数字水印解决方案，为扩散模型的身份认证与版权保护提供支持。