【c++知识铺子】map和set的底层-红黑树

爱装代码的小瓶子2025-12-11 8:31

关注我，学习c++不迷路:

个人主页：爱装代码的小瓶子

专栏如下：

  1. c++学习
  2. Linux学习

后续会更新更多有趣的小知识，关注我带你遨游知识世界

期待你的关注。

文章目录

1. 前言

在前一篇文章中 AVL树中我们也讲述了map和set的一种底层设计方式：通过平衡因子来控制树之间的平衡，这是一种通过规律强的数学公式来控制树的高度差。那么今天所要介绍的就是通过四个小规则来完成对二叉搜索树的平衡控制，很类似与规则怪谈，我们来详细看看：

  1. 每个节点是红色或黑色(毕竟我们都叫红黑树了)
  2. 根节点是黑色
  3. 红色节点的子节点必须是黑色（不能有两个连续的红色节点）
  4. 从任一节点到其每个叶子的所有路径包含相同数量的黑色节点（到空节点）

这四个规则就巧妙的控制了红黑树的平衡。

我们可以来理一理，如果一个节点最短的话，那么他最好就全是黑色节点，因为他要求每个路径的黑色节点相等，所以他最少也是全部都是黑色节点，其余路径或多或少有一些红色节点，那么他的最长的也出来了，那就是一黑一红相间其中，为2倍黑色的节点。那么其他的长度都介于这两者之间，虽然不如AVL树平衡严格，但是也是一种巧妙的平衡。这也是红黑树的两种特点：

  • 最长路径不超过最短路径的2倍
  • "近似平衡"而非严格平衡

我们打开STL源码，会发现map和set的底层竟然是红黑树。原因我们后面细细道来：

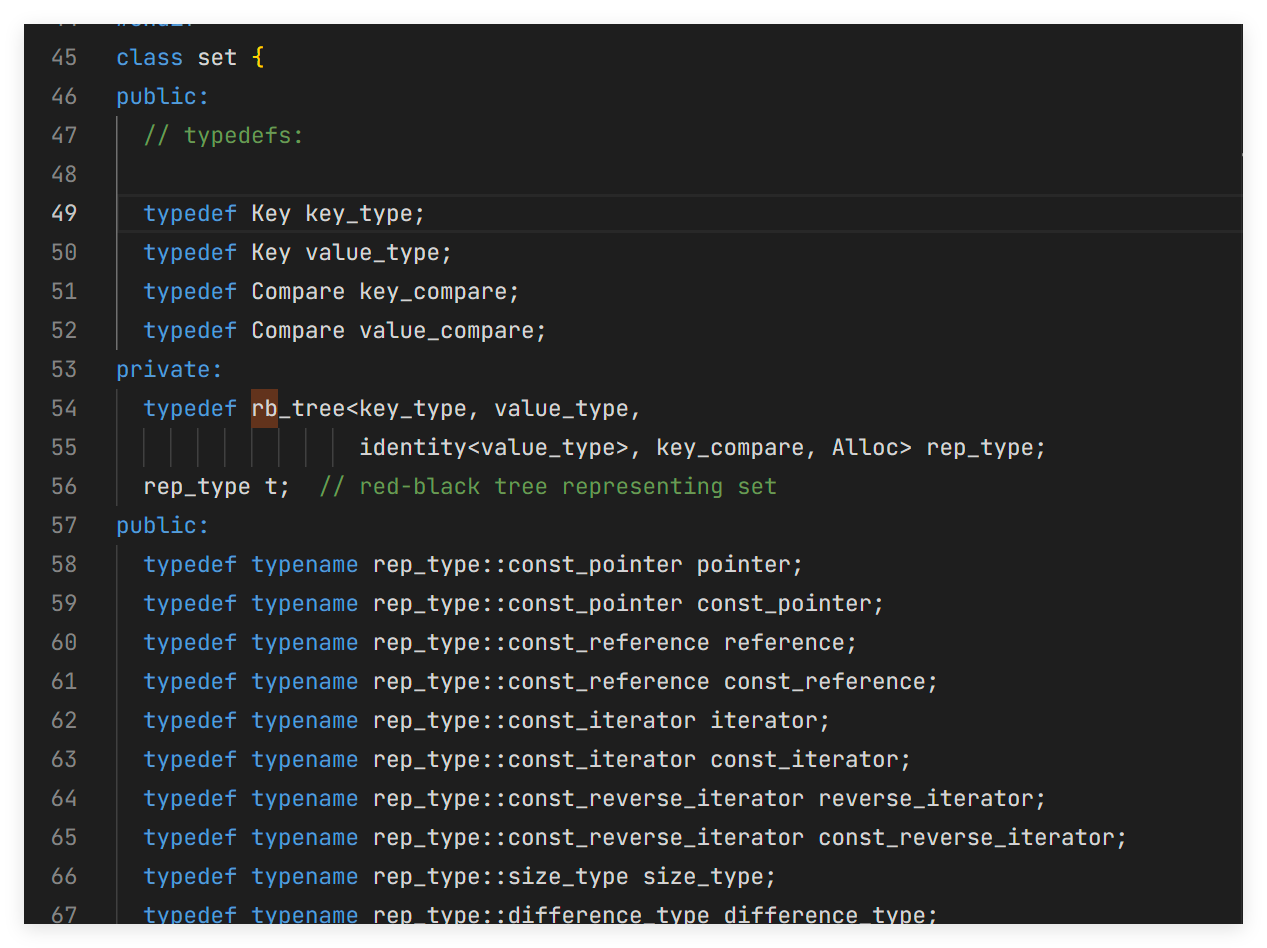
这里的rb_tree就是红黑树：

  • rb_tree 类型定义 ：set的内部使用 rb_tree （red-black tree，红黑树）作为底层数据结构
  • 注释说明 ：代码中的注释直接说明 "red-black tree representing set"
  • 成员变量 ：通过 rep_type t 创建了红黑树对象作为set的内部表示。

说了这么多，我们也来尝试实现自己的红黑树吧

2. 红黑树的结构：

依旧是定义节点，记住里面三个指针，分别指向父亲以及左右孩子，最后没有AVL树中的平衡因子，但是得有一个红黑颜色表示形态，这里可以使用枚举体来做为。

cpp 复制代码 
enum Color {
	BLACK,
	RED,
};

template<class K,class V>
class RBTreeNode {
public:
	RBTreeNode(const pair<K,V>& kv)
		:_kv(kv)
		,_parent(nullptr)
		,_left(nullptr)
		,_right(nullptr)
	{ }

	pair<K, V> _kv;
	RBTreeNode* _parent;
	RBTreeNode* _left;
	RBTreeNode* _right;
	Color _col;
};

完成对树中的每一个节点的结构设计，只需要把这些结构串联起来就行了，那么：

cpp 复制代码 
template <class K,class V>
class RBTree {
	using Node = RBTreeNode<K,V>;
private:
	Node* _root = nullptr;
};

这样就好了，暂时给根节点置为空（nullptr）

3. 插入函数：（重难点）

先定义一个节点指针cur，这个就是我们要插入的节点位置。在定于节点指针为parent，这个是便于后面的插入。

2-1：判断根节点：

如果_root 为空，直接将kv值变成_root,完成后续操作。

cpp 复制代码 
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

2-2 找寻cur的插入位置：

依旧很简单，如果在kv的值比该节点的值大就往由边走，如果小就往左边走：一直循环下去，如果相等，就直接不插入，放回false。

cpp 复制代码 
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
				return false;
		}

此时cur节点的位置就是我们需要插入的位置，我们在判断cur位置是parent的左边还是右边，（我们出来的时候是不知道cur的位置的）,同时我们默认插入的是红色节点，如果插入黑色节点会导致，每个路径的黑色节点数量不一致。

cpp 复制代码 
		cur = new Node(kv);
		if (kv.first < parent->_kv.first)
			parent->_left = cur;
		else
			parent->_right = cur;
		cur->_col = RED;//默认插入为红色，如果插入黑色不满足红黑树
		cur->_parent = parent;

此时插入会出现很多情况，我们后面详细讨论，此时依旧完成了前面的准备工作.

2-3 变色 O 旋转：

如果我们的父亲是黑色的，那么什么事情也不会发生。这是不违法红黑树的任何情况。

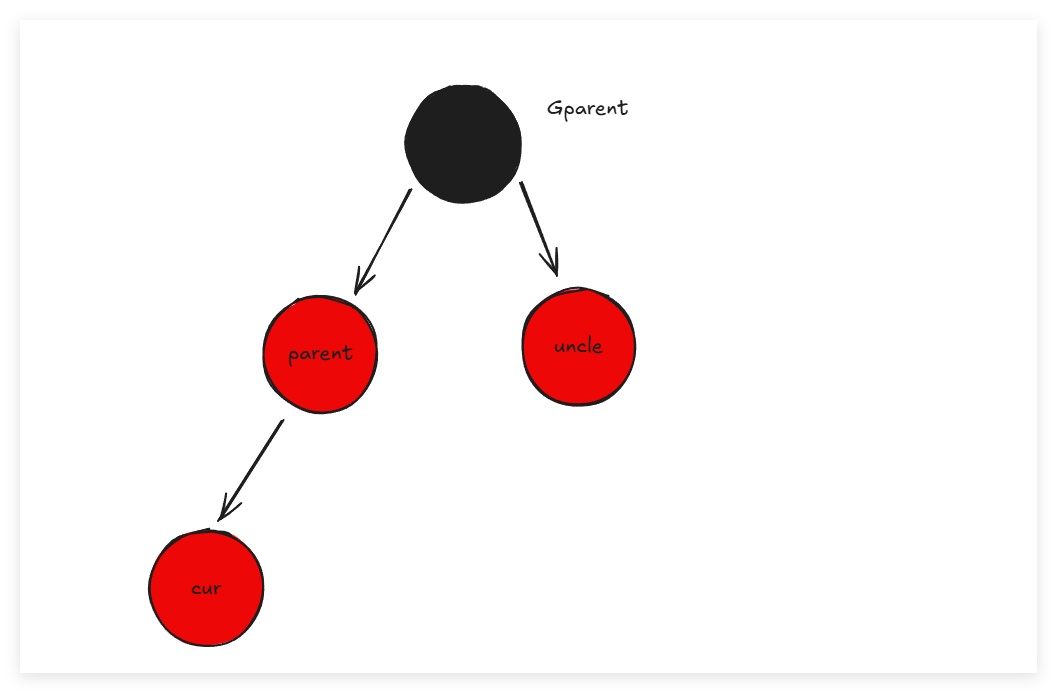
那么我们发现如果父亲是红色就麻烦了，那是因为不能出现连续的红色节点。此时可以又可以出现以下几种情况：

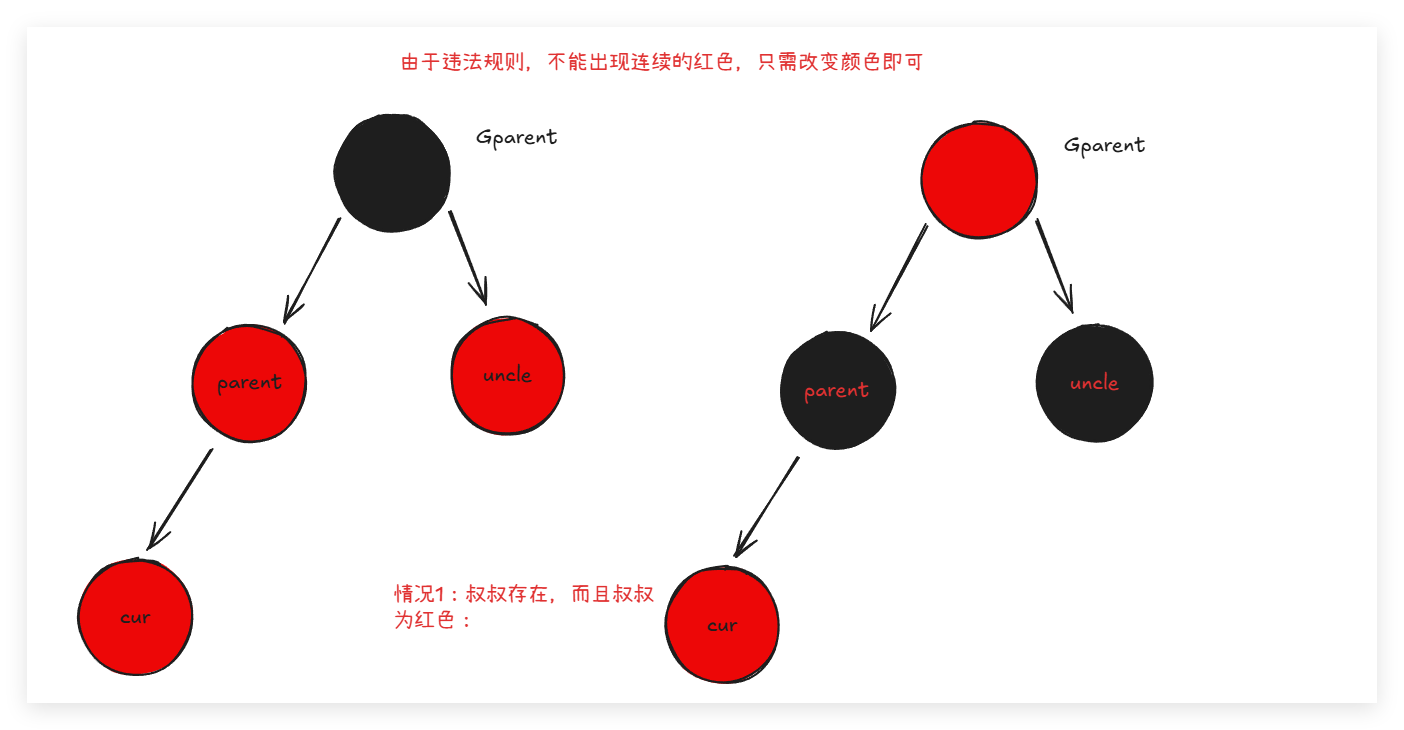
  1. 出现叔叔（父亲节点的兄弟节点）节点，而且节点为红色：此时只需要简单的变色：将叔叔和父亲变成黑色，而爷爷（父亲的父亲变成红色）。这样每个路径的黑色节点数量也没有变化，红色节点连续这件事也解决了。同时后面爷爷的父亲还是红色，还是出现了两个红色节点，还要继续在这个循环里面，变色直至根节点，或者出现其他情况：旋转+变色。

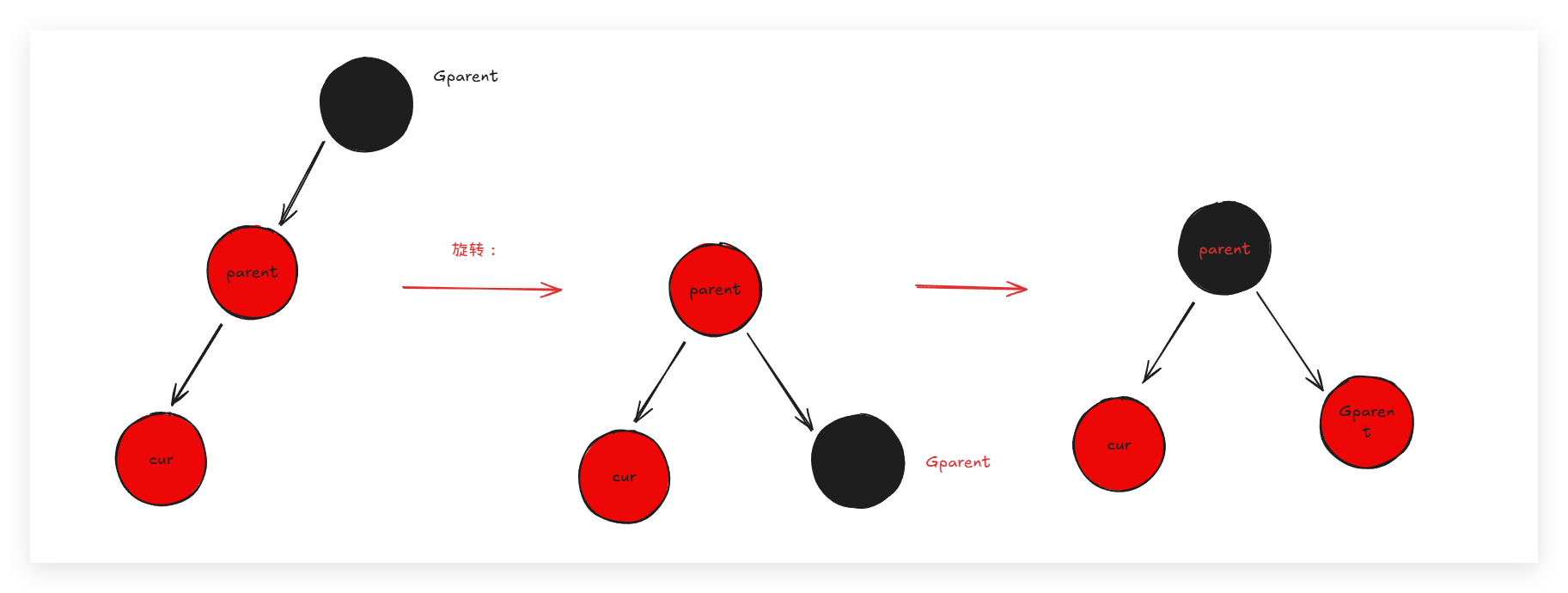
  2. 叔叔不存在或者叔叔是黑色。其中，叔叔不存在，说明cur是后面新插入的。不能存在cur是新插入的，而且叔叔还是黑色的。同时：叔叔是黑色，说明cur是通过前面的变色循环循环上来的：如果uncle是黑色的说明，cur不是新的插入，而是之前的变色循环导致cur是红色的，此时uncle是黑色的，与原本的cur一样是黑色。但是由于循环变色，导致G变色，此时G又变成了红色。但是这样的情况都说明：需要旋转了：这是比较简单的：





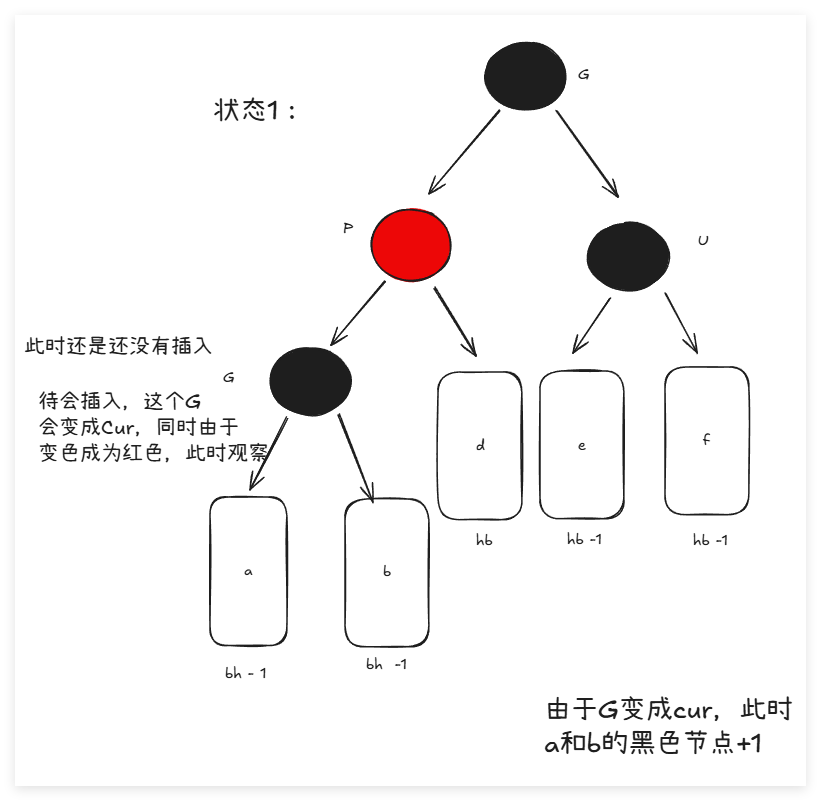
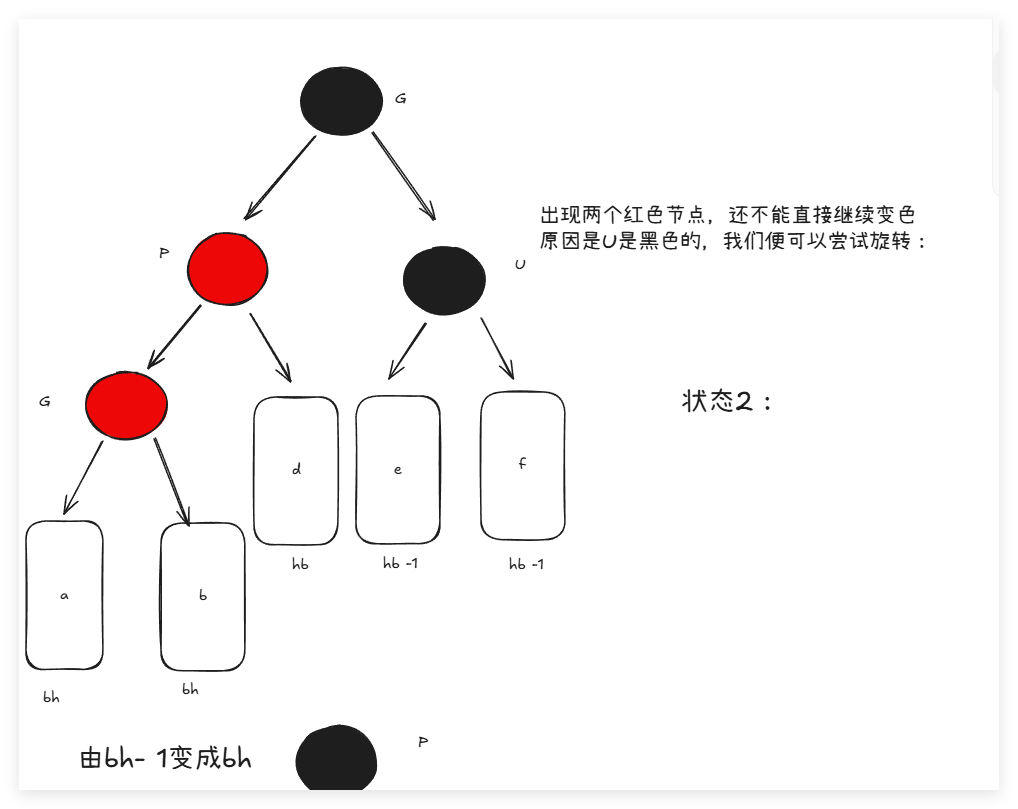
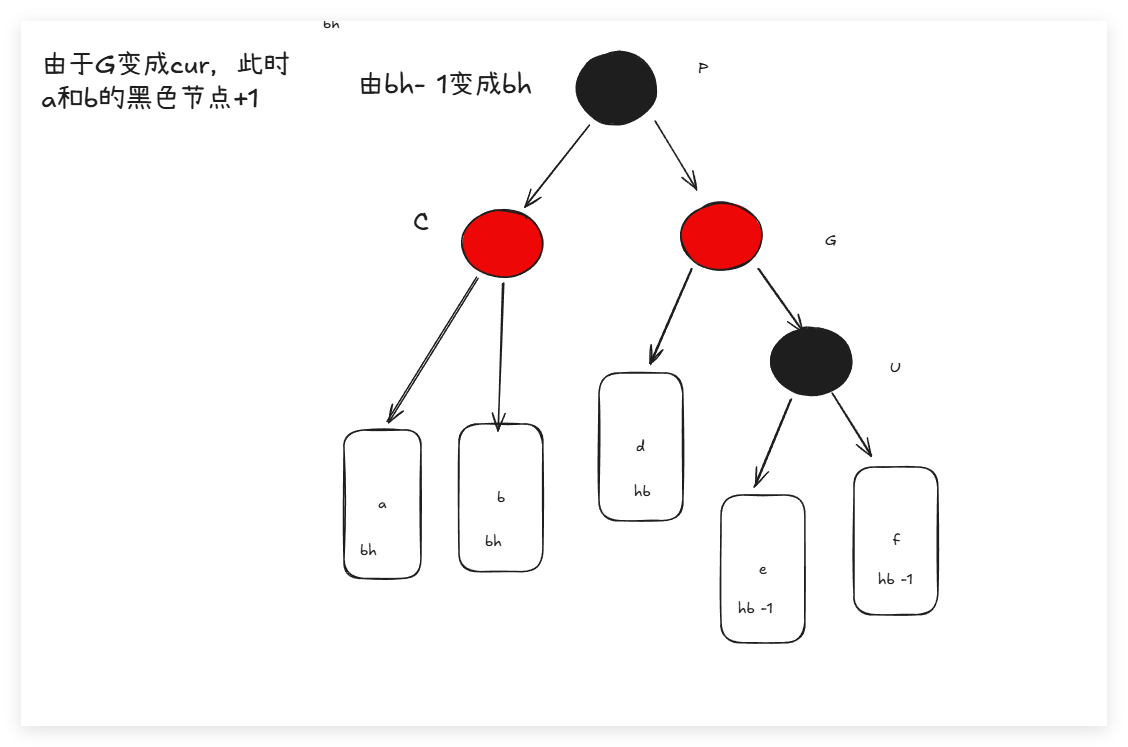
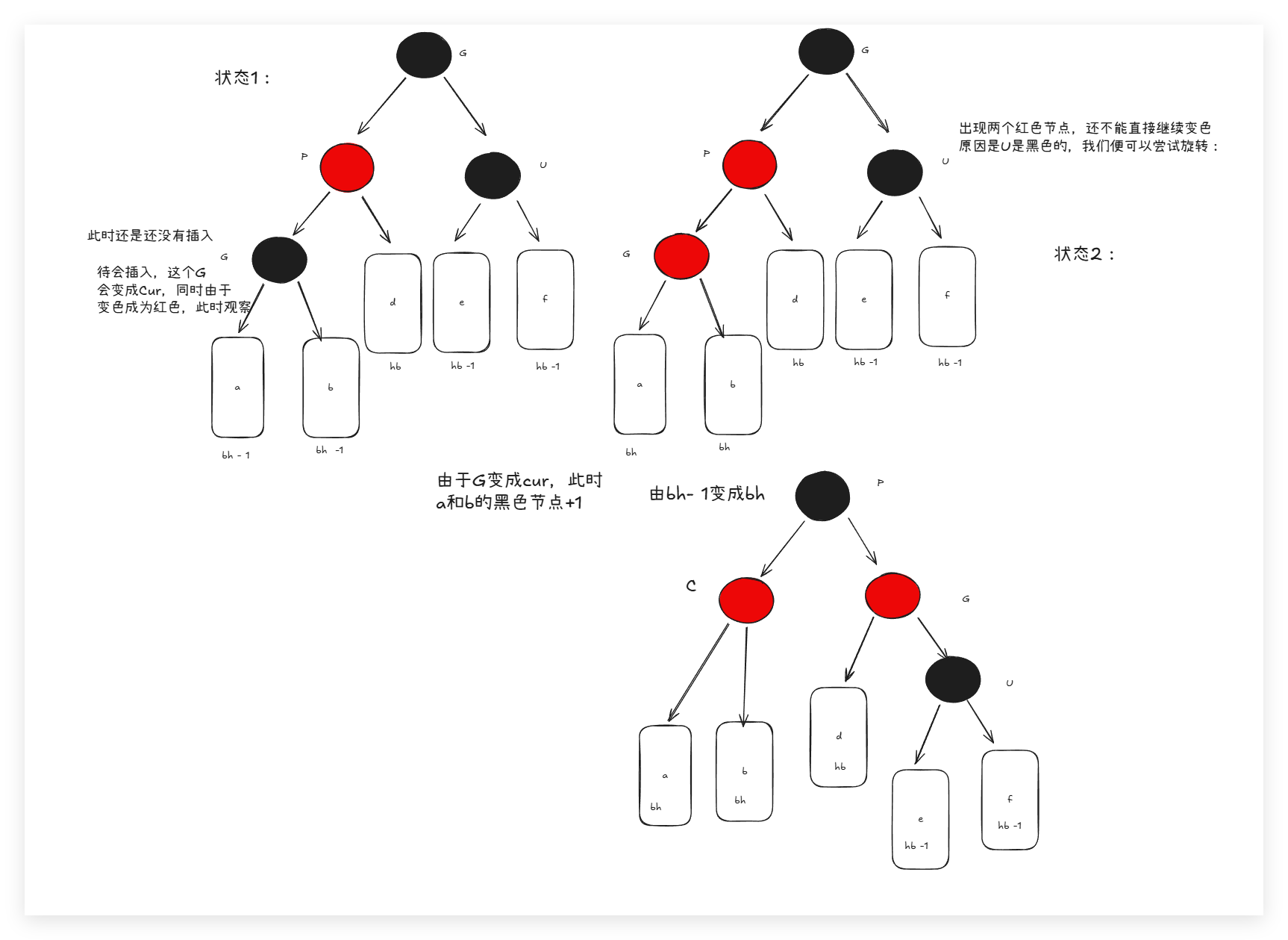
    这个很好的介绍了，单选，那么双选，就是不是一直的局部不高所导致的：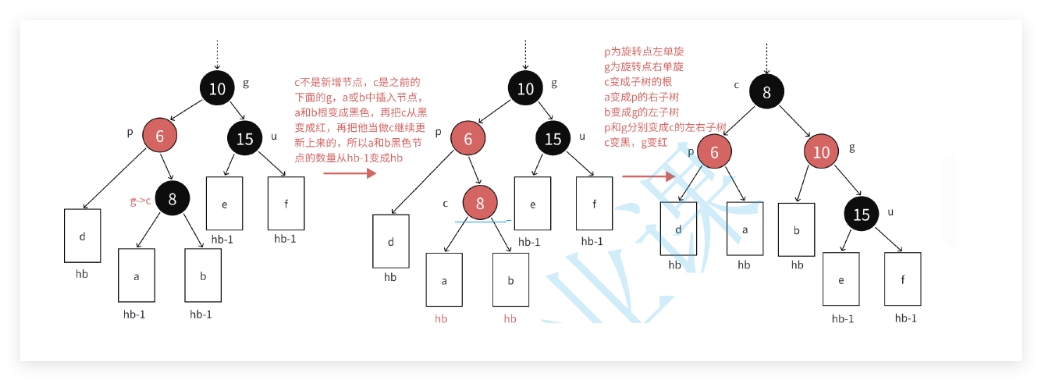

这时我们已经完成了插入函数的一大半了，情况1代码如下:

cpp 复制代码 
			if (Gparent->_left == parent)
			{
				//   G
				// p   u
				Node* uncle = Gparent->_right;
				if (uncle && uncle->_col == RED )
				{
					//开始变色：
					uncle->_col = BLACK;
					parent->_col = BLACK;
					Gparent->_col = RED;//注意事项

					cur = Gparent;
					parent = cur->_parent;
				}

情况二代码如下：

cpp 复制代码 
				else {
					//这里uncle不可能是黑色的，如果parent是红色的，那么uncle如果存在，就必须是红色的
					//  G
					//p   
					if (cur == parent->_left)
					{
						//    G
						//  p
						//c
						RotateR(Gparent);
						parent->_col = BLACK;
						Gparent->_col = RED;
					}
					else if (cur == parent->_right)
					{
						//    G
						//  p
						//   c
						RotateL(parent);
						RotateR(Gparent);
						Gparent->_col = RED;
						cur->_col = BLACK;//cur做了Gpa
					}
					//这里需不要break?之前需要更新是因为Gpanet的parent可能也是红色
					break;
				}
			}

为什么说完成了一大半，观察上面的代码，我们只关注了parent在Gparent的右边，那么两个位置呼唤呢，其实两个情况是一样的。左边和右边代码如下：

cpp 复制代码 
	//开始分类讨论：
	while (parent && parent->_col == RED)
	{
		Node* Gparent = parent->_parent;
		//如果父亲不是空并且父亲为红色就进入循环：
		if (Gparent->_left == parent)
		{
			//   G
			// p   u
			Node* uncle = Gparent->_right;
			if (uncle && uncle->_col == RED )
			{
				//开始变色：
				uncle->_col = BLACK;
				parent->_col = BLACK;
				Gparent->_col = RED;//注意事项

				cur = Gparent;
				parent = cur->_parent;
			}
			else {
				//这里uncle不可能是黑色的，如果parent是红色的，那么uncle如果存在，就必须是红色的
				//  G
				//p   
				if (cur == parent->_left)
				{
					//    G
					//  p
					//c
					RotateR(Gparent);
					parent->_col = BLACK;
					Gparent->_col = RED;
				}
				else if (cur == parent->_right)
				{
					//    G
					//  p
					//   c
					RotateL(parent);
					RotateR(Gparent);
					Gparent->_col = RED;
					cur->_col = BLACK;//cur做了Gpa
				}
				//这里需不要break?之前需要更新是因为Gpanet的parent可能也是红色
				break;
			}
		}
		else {
			//   G
			//u     P
			Node* uncle = Gparent->_left;
			if (uncle && uncle->_col == RED)
			{
				//开始变色：
				uncle->_col = parent->_col = BLACK;
				Gparent->_col = RED;
				cur = Gparent;
				parent = cur->_parent;
			}
			else {
				if (cur == parent->_right)
				{
					//  G
					//   p
					//      c
					RotateL(Gparent);
					parent->_col = BLACK;
					Gparent->_col = RED;
				}
				else {
					RotateR(parent);
					RotateL(Gparent);
					cur->_col = BLACK;
					Gparent->_col = RED;
				}
				break;
			}
		}
	}
	_root->_col = BLACK;//无论如何都要让_root变成黑色
	return true;
}

连在一起就是：

cpp 复制代码 
	bool insert(const pair<K,V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
				return false;
		}
		cur = new Node(kv);
		if (kv.first < parent->_kv.first)
			parent->_left = cur;
		else
			parent->_right = cur;
		cur->_col = RED;//默认插入为红色，如果插入黑色不满足红黑树
		cur->_parent = parent;

		//开始分类讨论：
		while (parent && parent->_col == RED)
		{
			Node* Gparent = parent->_parent;
			//如果父亲不是空并且父亲为红色就进入循环：
			if (Gparent->_left == parent)
			{
				//   G
				// p   u
				Node* uncle = Gparent->_right;
				if (uncle && uncle->_col == RED )
				{
					//开始变色：
					uncle->_col = BLACK;
					parent->_col = BLACK;
					Gparent->_col = RED;//注意事项

					cur = Gparent;
					parent = cur->_parent;
				}
				else {
					//这里uncle不可能是黑色的，如果parent是红色的，那么uncle如果存在，就必须是红色的
					//  G
					//p   
					if (cur == parent->_left)
					{
						//    G
						//  p
						//c
						RotateR(Gparent);
						parent->_col = BLACK;
						Gparent->_col = RED;
					}
					else if (cur == parent->_right)
					{
						//    G
						//  p
						//   c
						RotateL(parent);
						RotateR(Gparent);
						Gparent->_col = RED;
						cur->_col = BLACK;//cur做了Gpa
					}
					//这里需不要break?之前需要更新是因为Gpanet的parent可能也是红色
					break;
				}
			}
			else {
				//   G
				//u     P
				Node* uncle = Gparent->_left;
				if (uncle && uncle->_col == RED)
				{
					//开始变色：
					uncle->_col = parent->_col = BLACK;
					Gparent->_col = RED;
					cur = Gparent;
					parent = cur->_parent;
				}
				else {
					if (cur == parent->_right)
					{
						//  G
						//   p
						//      c
						RotateL(Gparent);
						parent->_col = BLACK;
						Gparent->_col = RED;
					}
					else {
						RotateR(parent);
						RotateL(Gparent);
						cur->_col = BLACK;
						Gparent->_col = RED;
					}
					break;
				}
			}
		}
		_root->_col = BLACK;//无论如何都要让_root变成黑色
		return true;
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* Pparent = parent->_parent;

		//第一步：处理subLR
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;
		//第二部处理：parent
		subL->_right = parent;
		parent->_parent = subL;
		//第三部处理Pparent和 subL
		subL->_parent = Pparent;
		if (Pparent == nullptr)
			_root = subL;
		else {
			if (parent == Pparent->_left)
				Pparent->_left = subL;
			else 
				Pparent->_right = subL;
		}
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* Pparent = parent->_parent;

		//1.处理：subRL 
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
		//2.处理：parent
		parent->_parent = subR;
		subR->_left = parent;
		//3.处理Pparent和subR；
		subR->_parent = Pparent;
		if (Pparent == nullptr)
			_root = subR;
		else {
			if (parent == Pparent->_left)
				Pparent->_left = subR;
			else
				Pparent->_right = subR;
		}
	}

4.IsRBTree（是不是红黑树）

如何判断他是不是一个红黑树，很简单。如果他的根不是黑色的，可以直接返回false。随后判断，他与他的父亲节点是不是都是红色的。

此时这些还不满足所以条件，我们可以去比较每个路径的黑色节点：先给一个确定值，最左边的黑色路径的黑色节点数量，

那么怎么比较呢，我们可以递归去比较，每次遇到空就开始比较：并返回对错：

cpp 复制代码 
	bool IsRBTree()
	{
		//可以直接判断，就直接在这里写：
		if (_root == nullptr)
			return true;
		if (_root->_col == RED)
			return false;
		int RefNum = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
				RefNum++;
			cur = cur->_left;
		}
		return _Check(_root, 0, RefNum);
	}
cpp 复制代码 
	bool _Check(Node* root, int BH, int RN)
	{
		if (root == nullptr)
		{
			if (BH != RN)
			{
				cout << "存在黑色结点的数量不相等的路径" << endl;
				return false;
			}
			return true;//控制递归返回条件。
		}
		if (root->_col == BLACK)
			BH++;
		if (root->_col == RED && root->_parent->_col == RED)
		{
			//如果是根节点，是不会找他的父节点，就不会空指针的解引用
			cout << "存在两个红色节点" << endl;
			return false;
		}
		return _Check(root->_left, BH, RN) && _Check(root->_right, BH, RN);
	}

5.树的高度：

第一种写法还是很简单的，就是每次找左右树的最大的高度，递归来完成：

cpp 复制代码 
	size_t _Height(Node* root)
	{
		if (root == nullptr)
			return 0;
		size_t LH = _Height(root->_left);
		size_t RH = _Height(root->_right);
		return 1 + max(LH, RH);
	}
cpp 复制代码 
	size_t Height()
	{
		return _Height(_root);
	}

第二种写法的优点是，树再高也不会栈溢出。这是借助queue的程序遍历：

有两个比较坑的点就是，不能直接使用for(int i = 0;i++;i < q.size())这是错误的，在循环里这个值一直在变化，会导致函数错误。

cpp 复制代码 
	size_t _Height(Node* root)
	{
		queue<Node*> q;
		q.push(root);
		size_t height = 0;
		while (!q.empty())
		{
			height++;
			//如果不为空
			size_t size = q.size();
			for (int i = 0; i < size; i++)
			{
				Node* node = q.front();
				if(node->_left)
					q.push(node->_left);
				if(node->_right)
					q.push(node->_right);
				q.pop();
			}
		}
		return height;
	}

6.红黑树的整体：

cpp 复制代码 
#pragma once
#include<iostream>
#include<cassert>
#include<cmath>
#include<queue>
using namespace std;

enum Color {
	BLACK,
	RED,
};

template<class K,class V>
class RBTreeNode {
public:
	RBTreeNode(const pair<K,V>& kv)
		:_kv(kv)
		,_parent(nullptr)
		,_left(nullptr)
		,_right(nullptr)
	{ }

	pair<K, V> _kv;
	RBTreeNode* _parent;
	RBTreeNode* _left;
	RBTreeNode* _right;
	Color _col;
};

template <class K,class V>
class RBTree {
	using Node = RBTreeNode<K,V>;
public:
	bool insert(const pair<K,V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
				return false;
		}
		cur = new Node(kv);
		if (kv.first < parent->_kv.first)
			parent->_left = cur;
		else
			parent->_right = cur;
		cur->_col = RED;//默认插入为红色，如果插入黑色不满足红黑树
		cur->_parent = parent;

		//开始分类讨论：
		while (parent && parent->_col == RED)
		{
			Node* Gparent = parent->_parent;
			//如果父亲不是空并且父亲为红色就进入循环：
			if (Gparent->_left == parent)
			{
				//   G
				// p   u
				Node* uncle = Gparent->_right;
				if (uncle && uncle->_col == RED )
				{
					//开始变色：
					uncle->_col = BLACK;
					parent->_col = BLACK;
					Gparent->_col = RED;//注意事项

					cur = Gparent;
					parent = cur->_parent;
				}
				else {
					//这里uncle不可能是黑色的，如果parent是红色的，那么uncle如果存在，就必须是红色的
					//  G
					//p   
					if (cur == parent->_left)
					{
						//    G
						//  p
						//c
						RotateR(Gparent);
						parent->_col = BLACK;
						Gparent->_col = RED;
					}
					else if (cur == parent->_right)
					{
						//    G
						//  p
						//   c
						RotateL(parent);
						RotateR(Gparent);
						Gparent->_col = RED;
						cur->_col = BLACK;//cur做了Gpa
					}
					//这里需不要break?之前需要更新是因为Gpanet的parent可能也是红色
					break;
				}
			}
			else {
				//   G
				//u     P
				Node* uncle = Gparent->_left;
				if (uncle && uncle->_col == RED)
				{
					//开始变色：
					uncle->_col = parent->_col = BLACK;
					Gparent->_col = RED;
					cur = Gparent;
					parent = cur->_parent;
				}
				else {
					if (cur == parent->_right)
					{
						//  G
						//   p
						//      c
						RotateL(Gparent);
						parent->_col = BLACK;
						Gparent->_col = RED;
					}
					else {
						RotateR(parent);
						RotateL(Gparent);
						cur->_col = BLACK;
						Gparent->_col = RED;
					}
					break;
				}
			}
		}
		_root->_col = BLACK;//无论如何都要让_root变成黑色
		return true;
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* Pparent = parent->_parent;

		//第一步：处理subLR
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;
		//第二部处理：parent
		subL->_right = parent;
		parent->_parent = subL;
		//第三部处理Pparent和 subL
		subL->_parent = Pparent;
		if (Pparent == nullptr)
			_root = subL;
		else {
			if (parent == Pparent->_left)
				Pparent->_left = subL;
			else 
				Pparent->_right = subL;
		}
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* Pparent = parent->_parent;

		//1.处理：subRL 
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
		//2.处理：parent
		parent->_parent = subR;
		subR->_left = parent;
		//3.处理Pparent和subR；
		subR->_parent = Pparent;
		if (Pparent == nullptr)
			_root = subR;
		else {
			if (parent == Pparent->_left)
				Pparent->_left = subR;
			else
				Pparent->_right = subR;
		}
	}

	void Inorder()
	{
		_Inorder(_root);
	}

	void Find(const pair<K, V>& kv)
	{
		if (_root = nullptr)
			return false;
		Node* cur = _root;

		if (kv.first > cur->_kv.first)
			cur = cur->_right;
		else if (kv.first < cur->_kv.first)
			cur = cur->_left;
		else
		{
			cout << cur->_kv.first << ":" << cur->_kv.second << endl;
			return true;
		}
		return false;
	}

	bool IsRBTree()
	{
		//可以直接判断，就直接在这里写：
		if (_root == nullptr)
			return true;
		if (_root->_col == RED)
			return false;
		int RefNum = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
				RefNum++;
			cur = cur->_left;
		}
		return _Check(_root, 0, RefNum);
	}

	size_t Size()
	{
		return _Size(_root);
	}

	size_t Height()
	{
		return _Height(_root);
	}


private:
	void _Inorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << endl;
		_Inorder(root->_right);
	}

	bool _Check(Node* root, int BH, int RN)
	{
		if (root == nullptr)
		{
			if (BH != RN)
			{
				cout << "存在黑色结点的数量不相等的路径" << endl;
				return false;
			}
			return true;//控制递归返回条件。
		}
		if (root->_col == BLACK)
			BH++;
		if (root->_col == RED && root->_parent->_col == RED)
		{
			//如果是根节点，是不会找他的父节点，就不会空指针的解引用
			cout << "存在两个红色节点" << endl;
			return false;
		}
		return _Check(root->_left, BH, RN) && _Check(root->_right, BH, RN);
	}

	size_t _Size(Node* root)
	{
		if (root == nullptr)
			return 0;
		//没遍历一个都会加1.
		return _Size(root->_left) + _Size(root->_right) + 1;
	}

	//size_t _Height(Node* root)
	//{
	//	if (root == nullptr)
	//		return 0;
	//	size_t LH = _Height(root->_left);
	//	size_t RH = _Height(root->_right);
	//	return 1 + max(LH, RH);
	//}
		
	size_t _Height(Node* root)
	{
		queue<Node*> q;
		q.push(root);
		size_t height = 0;
		while (!q.empty())
		{
			height++;
			//如果不为空
			size_t size = q.size();
			for (int i = 0; i < size; i++)
			{
				Node* node = q.front();
				if(node->_left)
					q.push(node->_left);
				if(node->_right)
					q.push(node->_right);
				q.pop();
			}
		}
		return height;
	}


	Node* _root = nullptr;
};

3. 总结：

核心要点回顾：

  1. 通过四个简单规则实现近似平衡（非严格平衡）
  2. 最长路径不超过最短路径的2倍
  3. 牺牲一点查找性能换取更好的插入/删除性能

为什么要使用红黑树：

对比维度 红黑树 AVL树
平衡严格度 近似平衡 严格平衡
插入/删除 最多3次旋转 可能O(log n)次旋转
查找性能 O(log n) 略慢 O(log n) 更快
适用场景 频繁更新 查找为主

红黑树不仅是数据结构，更是工程智慧的结晶。它教会我们在复杂系统中寻找简单有效的约束，在严格与灵活之间找到平衡点。掌握红黑树，不仅掌握了一种数据结构，更掌握了一种系统设计思想。

进一步学习：

  1. 《算法导论》：红黑树经典论述
  2. STL源码剖析：工业级实现
  3. Linux内核源码：实际应用案例
相关推荐
电商API&Tina4 分钟前
【电商API接口】多电商平台数据API接入方案（附带实例）
运维·开发语言·数据库·chrome·爬虫·python·jenkins
叫我莫言鸭8 分钟前
关于word生成报告的POI学习2循环标题内容
java·学习·word
1001101_QIA8 分钟前
【C++笔试题】递归判断数组是否是递增数组
开发语言·c++
zhangx1234_10 分钟前
C语言 题目2
c语言·开发语言
七夜zippoe12 分钟前
Spring与MyBatis整合原理及事务管理
java·spring·mybatis·事务·mapper
YJlio14 分钟前
网络与通信具总览（14.0）：从 PsPing 到 TCPView / Whois 的联合作战
开发语言·网络·php
yong999015 分钟前
超宽带系统链路 MATLAB 仿真
开发语言·算法·matlab
yaoxin52112316 分钟前
278. Java Stream API - 限制与跳过操作全解析
java·开发语言·python
iCheney！20 分钟前
php生成赛博像素风头像
开发语言·php
短剑重铸之日24 分钟前
《深入解析JVM》第五章：JDK 8之后版本的优化与JDK 25前瞻
java·开发语言·jvm·后端
热门推荐
01GitHub 镜像站点02Linux下V2Ray安装配置指南03jdk21下载、安装（Windows、Linux、macOS）04Claude Code Skills 实用使用手册05从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击06UV安装并设置国内源072025 最新教程：注册并切换到美区 Apple ID08【踩坑笔记】50系显卡适配的 PyTorch 安装09祝大家 2026 年新年快乐，代码无 bug，需求一次过10Google Antigravity Agent 编辑器操作教程