摘要
单源域泛化目标检测(SDGOD)作为计算机视觉领域的前沿研究课题,旨在通过单源域训练增强模型在未见目标域中的泛化能力。当前主流方法试图通过数据增强技术来减轻域差异。然而,由于域偏移和有限的域特定知识,模型往往陷入虚假相关性的陷阱。这表现为模型过度依赖简单的分类特征(如颜色),而非像物体轮廓这样的基本域不变表示。为应对这一关键挑战,我们提出了Cauvis(因果视觉提示)方法。首先,我们引入了交叉注意力提示模块,通过将视觉提示与交叉注意力相结合,减轻虚假特征的偏差。为了解决单域泛化中视觉提示的域知识覆盖不足和虚假特征纠缠问题,我们提出了一种双分支适配器,通过高频特征提取解耦因果-虚假特征,同时实现域适应。Cauvis在SDGOD数据集上实现了最先进的性能,比现有的域泛化方法提高了15.9-31.4%,同时在复杂干扰环境中表现出显著的鲁棒性优势。
https://arxiv.org/pdf/2510.19487
1 引言
自动驾驶目标检测模型面临着复杂目标和多变天气条件的挑战,其中域偏移显著降低了检测精度。与开放集[1]或少样本目标检测[2]相比,单域泛化目标检测(SDGOD)[3]仅依赖单源域数据进行训练,没有跨域先验知识(既无多域训练数据,也无目标域提示)------在遇到域偏移时表现出严重的过拟合。这已成为限制自动驾驶感知系统实际部署的关键瓶颈。
SDGOD的核心挑战在于在多域场景下实现精确的多目标定位和识别。此类任务中的机器学习模型容易受到训练数据偏差的影响,过度依赖目标标签与背景噪声/次要特征之间的虚假相关性。这些虚假相关性通过两种相互关联的机制产生:空间上,由于训练数据主要将车辆置于图像中心区域(Cityscapes[4]主车道场景特征)并将行人置于边缘附近(典型人行道区域),模型错误地建立了"vehicle-center"空间绑定,同时将行人严格锚定在边缘区域,从而忽略了现实世界物体分布的自然变化。同时,颜色偏差通过误导性的颜色-类别关联出现,特别是将白色色调与公交车/卡车联系起来(BDD100K[5]城市交通常见涂装),以及将黑色物体与汽车关联。关键的是,这些基于表面特征的虚假相关性导致模型在分布外(OOD)场景中的泛化性能显著下降。尽管最近的工作如UFR[6]试图通过因果注意力学习来解决场景混杂因素,但它们对Faster R-CNN[7]框架的依赖和启发式扰动策略限制了在解耦因果特征方面的理论基础。
虽然现有研究利用域不变表示理论[3]来增强OOD泛化,但对虚假相关性的系统分析仍未得到充分解决。当前方法[3, 6, 8, 16]主要采用两种互补策略:域不变约束,从架构上将不变特征与域特定特征解耦[6];以及数据增强方法[3, 9],通过模拟多样化的域分布,通过扩展特征空间覆盖范围来抑制有偏特征依赖。然而,这些经验驱动的解决方案缺乏统一的理论基础,通常将模型缺陷归因于症状性偏差(数据倾斜/注意力分配错误/原型失真),而不是解决根本问题------单域训练数据中虚假相关性的固有普遍性。
为解决这些问题,我们提出了Cauvis(因果视觉提示)方法,其核心创新包括:交叉注意力提示,从数学上建立视觉提示与因果推断中后门调整操作[10]的等价性,为缓解虚假相关性提供理论基础;以及设计双分支适配器,通过系统表示解耦解耦因果/虚假特征,同时增强跨域知识覆盖。具体而言,它集成了傅里叶变换,通过高频分量提取实现因果特征解耦,同时结合非线性特征建模模块来增强提示的域分布覆盖能力。
我们的主要贡献是:
- 我们首次将DINOv2[11]作为骨干网络引入到SDGOD中。通过冻结参数减少训练成本,大量实验验证了这种方法显著增强了检测器性能。
- 通过理论分析和实验观察,我们将虚假相关性与泛化性能下降联系起来,建立了一个SDGOD的新理论框架。
- 我们提出了具有理论分析的交叉注意力提示,证明其等价于用于抑制虚假相关性的后门调整机制。此外,我们设计了一个双分支适配器,通过显式因果关系建模解决了传统方法在域知识覆盖和特征解耦方面的局限性。
2 相关工作
单域泛化目标检测
在SGDOD领域,现有方法主要关注两种策略:1)施加域特定约束以提取域不变表示;2)通过系统性数据增强增强输入多样性。CDSD[3]引入循环解耦自蒸馏框架,通过多阶段损失约束解耦域不变表示。OA-DG[12]采用多级变换和目标感知混合策略,减少域间表示差异。SRCD[9]构建自增强复合域,减轻类别-背景偏差。UFR[6]利用物理启发的数据增强来模拟潜在域分布。ClipGap[13]利用CLIP模型[14]的跨模态提示,实现语义引导增强。G-NAS[8]通过可微神经架构搜索优化域不变约束。我们的工作在不引入人工合成训练样本的情况下实现了高效泛化。
视觉提示
为减轻跨域差异,受NLP中提示学习启发的视觉提示(VP)[15]已成为一种高效的适应范式。它引入轻量级可调参数,通常只优化1%的模型权重,以适应下游任务。在少样本任务中,VP[16]通过稀疏标注的扰动机制(如空间注意力引导的局部增强)增强模型对新类别的适应性。视觉提示调优(VPT)[17]是一种代表性方法,在Transformer层中嵌入可学习提示向量,实现用于参数适应的分层特征交互。Rein[18]是一种高效的参数调优方法,本质上是一种独特的视觉提示形式。这些传统的VP方法[17-19]将提示特征与冻结骨干网络耦合,没有显式的因果/虚假解耦机制。
我们的方法与NLP提示机制有根本不同:NLP利用离散语义操作(如"MATCH"标记预测)进行文本重建,而视觉提示在连续像素空间中通过频域扰动或对抗性噪声注入来激活预训练VFM中的跨域知识。
3 动机
3.1 虚假相关性的实验展示
在图像分类任务[20-22]中,模型由于过度依赖训练数据中的虚假相关性,往往遭受OOD泛化性能下降。这个问题在密集检测任务中尤为关键:当模型关注非因果域特定特征(如背景或颜色)时,这些特征与标签偶然相关,而不是物体的内在因果特征,它们在未见域中的性能显著下降。
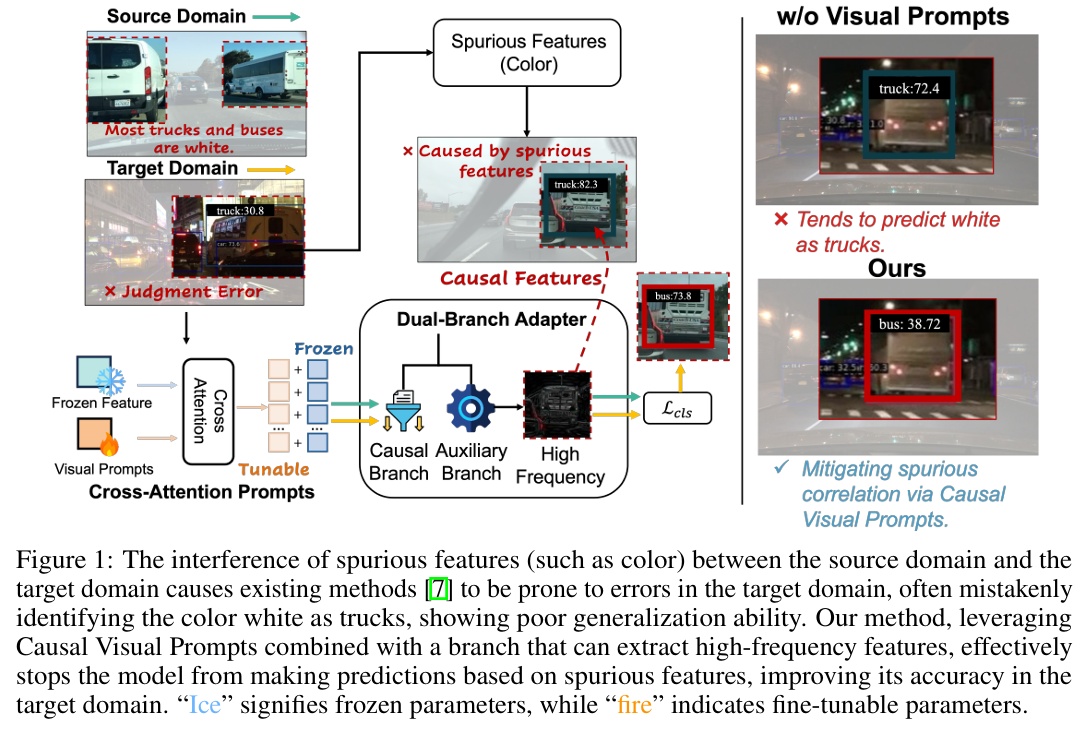
为了清晰说明这个问题,我们选择公交车和卡车类别作为代表性样本进行分析。这些类别在不同域中通常具有相同的颜色,主要呈现白色。(见图1)。为了创建受控实验环境,我们将这些类别的图像裁剪到任务相关区域,并过滤掉具有众多其他检测对象的图像,简化实验条件。
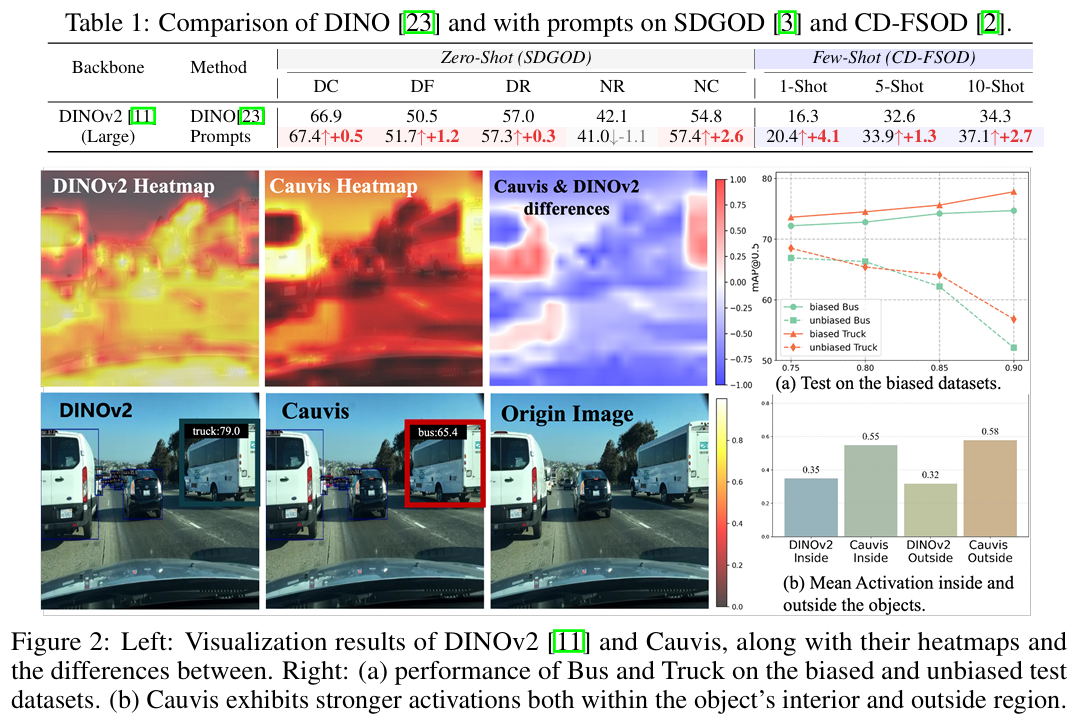
在实验设计中,我们人为增加颜色-类别关联的概率pip_ipi(即,提高卡车类别中白色颜色的概率到pip_ipi),并确保另一个类别(公交车)的非白色分布为1−pi1-p_i1−pi。基于不同的偏置强度,我们创建了具有不同偏置水平的几个数据集(pi∈[0.75,0.8,0.85,0.9]p_i \in [0.75,0.8,0.85,0.9]pi∈[0.75,0.8,0.85,0.9]),并将原始测试数据作为无偏测试。我们在四个有偏数据集上训练和测试,然后在无偏数据集上重新测试结果。如图2所示,模型对颜色特征的依赖性发生变化。当pip_ipi从0.75上升到0.9时,卡车的实验精度提高了4.2%,但无偏测试集上的卡车mAP下降了21%,表明模型对颜色捷径的依赖性更强。
值得注意的是,随着pip_ipi增加,模型在有偏测试集上获得更高的mAP,表明其越来越依赖简单的颜色-类别相关性进行决策。我们的对照实验表明,检测模型可能过度依赖颜色或背景相关性,特别是当训练数据存在系统性偏差时。虽然全面量化这个问题具有挑战性,但这些观察提供了关键见解,并揭示了先前研究中被忽视的线索。
视觉提示提供超越像素的语义约束。通过描述物体的基本属性,如其几何形状或结构体积,它们指导模型形成域不变的因果表示。这有助于模型避免依赖训练数据中的统计捷径。
3.2 视觉提示与因果表示
从因果表示学习的角度,我们可以将输入特征表示分解为因果部分fC(x)f_C(x)fC(x)和虚假部分fS(x)f_S(x)fS(x)。目标是使模型对fC(x)f_C(x)fC(x)敏感,但对fS(x)f_S(x)fS(x)鲁棒或能够忽略它。一种常见策略是通过在输入上应用扰动δ∼p(Δ)\delta \sim p(\Delta)δ∼p(Δ)来引入干预,模拟不同环境中的观察------例如,通过人为改变背景或添加噪声(x′=x+δ)(x' = x + \delta)(x′=x+δ),从而迫使模型关注稳定特征fC(x+δ)f_C(x+\delta)fC(x+δ)[24,25]。
现有工作[24]表明,如果模型只能使用纯因果信息(如前景区域的表示)进行预测,这等同于对系统执行因果干预,可以大大提高在分布外(OOD)场景下的性能。例如,CFA[24]只在包含前景(因果特征)的图像表示上进行训练,等同于执行因果干预。这有效地减少了虚假特征对预测的影响。
视觉提示[26]通过随机初始化(例如,通过连接)直接作为额外输入参数引入模型。在初始化时,这些提示向量δ\deltaδ只是随机噪声,但在训练过程中,它们通过反向传播更新,以最小化fC(x)f_C(x)fC(x)上的因果不变损失。实际上,优化将δ\deltaδ推向与fCf_CfC相同的低维因果子空间,并远离虚假方向。任何无法驱动fC(x+δ)≈fC^(x)f_C(x+\delta) \approx \hat{f_C}(x)fC(x+δ)≈fC^(x)的提示都会变得次优,可以被剪枝或重新初始化。在因果不变性假设下(见附录C),当提示收敛到其最优值p∗p^*p∗时,我们有
∂fC(x+δ)∂δ∣p=p∗=0.\left.\frac{\partial f_{C}(x+\delta)}{\partial\delta}\right|_{p=p^{*}}=0.∂δ∂fC(x+δ) p=p∗=0.
即,因果特征在此扰动下的梯度消失,表明提示不破坏原始因果结构[27]。此外,通过应用一阶泰勒展开,我们得到fC−(x+δ)=fC(x)+o(δ)f_C^-(x+\delta)=f_C(x)+o(\delta)fC−(x+δ)=fC(x)+o(δ),这表明当扰动δ\deltaδ足够小时,因果特征fCf_CfC的变化可以忽略不计。换句话说,提示引入的微小扰动不会破坏原始因果结构。
从频域角度看,F\mathcal{F}F和F−1\mathcal{F}^{-1}F−1是傅里叶变换及其逆变换,我们可以表达:
fC(x)=F−1(Hcausal⊙F(x))f_{C}(x)=\mathcal{F}^{-1}\big(H_{\mathrm{causal}}\odot\mathcal{F}(x)\big)fC(x)=F−1(Hcausal⊙F(x))
提示引入的扰动主要集中在低频区域,而滤波器函数Hcausal(ω)H_{\mathrm{causal}}(\omega)Hcausal(ω)对这些低频分量的响应接近零。因此,它同样不影响结果的因果特征。我们将视觉提示(初始化为零)建模为应用于图像低频分量的随机扰动。通过对因果不变性的分析,我们发现它们抑制虚假特征,同时保留因果信息。此外,通过进一步结合因果推断技术如后门调整[10],它们可以增强这些因果特征。
4 方法
我们提出了Cauvis,包括交叉注意力提示(第4.1节)和双分支适配器(第4.2节),如图3所示。它使用可学习参数动态调整预训练知识和视觉提示的融合比例。
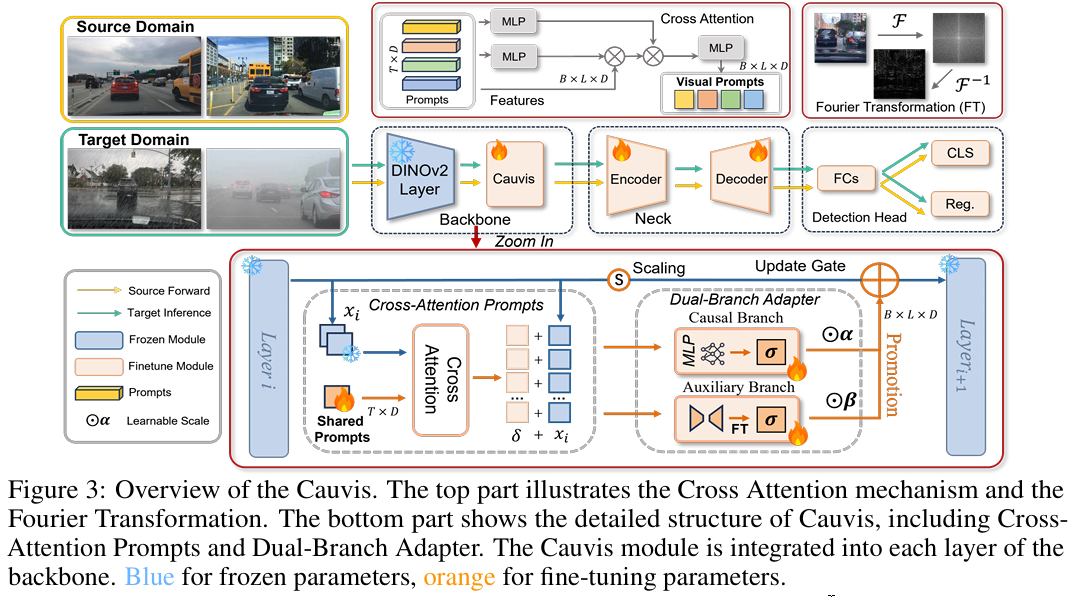
4.1 交叉注意力提示
我们提出了交叉注意力提示,以解决现有方法在因果推理和域泛化方面的局限性。我们的框架(如图1所示)使用交叉注意力将提示与特征链接起来。与先前工作不同(例如,Rein[18]的基于令牌的提示,EVP[28]的边缘嵌入,SPT[19]/VPT[17]依赖数据集驱动的提示初始化),我们将提示视为独立于图像域的伪模态信号。这种设计通过交叉注意力实现了因果干预。
根据Pearl的因果理论[10],对XXX进行干预产生结果分布P(y^∣do(X))P(\hat{y}|\mathrm{do}(X))P(y^∣do(X))。当混杂因素zzz阻断所有非因果X→yˉX\to{\bar{y}}X→yˉ路径时,后门调整公式为:
P(y^∣do(X))=∑zP(y^∣X,z)P(z).P(\hat{y}|\mathrm{do}(X))=\sum_{z}P(\hat{y}|X,z)P(z).P(y^∣do(X))=z∑P(y^∣X,z)P(z).
这调整了混杂因素zzz以消除非因果依赖。
在每个注意力层中,我们考虑注意力权重矩阵A ∈ RT×TA\;\in\;\mathbb{R}^{T\times T}A∈RT×T(省略批量维度)并计算其奇异值分解(SVD)ˉ,A=UΣV′\bar{(\mathbf{SVD})},A=U\Sigma V^{'}(SVD)ˉ,A=UΣV′ A=UΣV⊤,where U,V∈RT×TA=U\Sigma V^{\top},{\mathrm{where}}\;U,V\in\mathbb{R}^{T\times T}A=UΣV⊤,whereU,V∈RT×T和£是对角矩阵,具有非负奇异值。我们对A ˉ= UΣV\bar{A\,}=\,U\Sigma VAˉ=UΣV执行奇异值分解(SVD),其中U ∈ RT×Tˉ and V ∈ RT×TˉU\:\in\:\bar{\mathbb{R}^{T\times T}}\ \mathrm{and}\ V\:\in\:\bar{\mathbb{R}^{T\times T}}U∈RT×Tˉ and V∈RT×Tˉ是正交矩阵(T是令牌长度);Σ=diag(σ1,...,σT),and σ1≥σ2≥⋯≥0\Sigma=\operatorname{diag}(\sigma_{1},\dots,\sigma_{T}),{\mathrm{and}}\;\sigma_{1}\geq\sigma_{2}\geq\cdots\geq0Σ=diag(σ1,...,σT),andσ1≥σ2≥⋯≥0。SVD在注意力图中提供了一个正交基"方向",其中每个奇异值σı\sigma_{\imath}σ表示该分量的重要性或强度,在数据科学术语中,最大的奇异值捕获AAA中的主导表示。根据我们的假设,模型表示中的因果特征形成一个低维子空间,我们期望它们在AAA中产生大尺度分量。相比之下,虚假或噪声相关性只应贡献较小的奇异值。这种直觉符合最近对Transformer注意力的分析:Franco等人[29]假设,当注意力头关注特定低维特征时,例如"间接对象识别"任务,只有少数奇异值变得很大,导致稀疏分解。
基于此,我们明确将∑划分为因果和非因果子空间。具体来说,让Σc=diag(σ1,...,σk−)\Sigma_{c}=\mathrm{diag}(\sigma_{1},\dots,\sigma_{k}^{-})Σc=diag(σ1,...,σk−)包含kkk个最大奇异值,Σc⊥=diag(σk+1,...,σT)\Sigma_{c^{\perp}}=\mathrm{diag}(\sigma_{k+1},\dots,\sigma_{T})Σc⊥=diag(σk+1,...,σT)包含其余奇异值。TTT表示矩阵(或特征空间)的维度(或最大秩)。然后我们写成:
Ac=U(Σc000)V⊤,Ac⊥=U(000Σc⊥)V⊤,A=Ac+Ac⊥,A=UcΣcVc⊤+Uc⊥Σc⊥Vc⊥⊤.\begin{array}{r l}&{A_{c}=U\left(\begin{matrix}{\Sigma_{c}}&{0}\\ {0}&{0}\end{matrix}\right)V^{\top},\qquad A_{c^{\perp}}=U\left(\begin{matrix}{0}&{0}\\ {0}&{\Sigma_{c^{\perp}}}\end{matrix}\right)V^{\top},}\\ &{A=A_{c}+A_{c^{\perp}},\qquad A=U_{c}\Sigma_{c}V_{c}^{\top}+U_{c^{\perp}}\Sigma_{c^{\perp}}V_{c^{\perp}}^{\top}.}\end{array}Ac=U(Σc000)V⊤,Ac⊥=U(000Σc⊥)V⊤,A=Ac+Ac⊥,A=UcΣcVc⊤+Uc⊥Σc⊥Vc⊥⊤.
直观上,AcA_{c}Ac将注意力投影到由前kkk个奇异向量张成的低秩子空间(因果子空间)上,而AcA_{c}Ac包含残余"噪声"分量。关键的是,我们不是通过硬阈值固定kkk,而是将此分解集成到训练中:优化过程隐式确定有效秩。通过惩罚⋅ Σc⊥\cdot\,\,\Sigma_{c\perp}⋅Σc⊥的幅度,我们鼓励模型将其大部分权重放在AcA_{c}Ac中,避免手动截断。这个目标在奇异值上充当软阈值算子。
总体而言,因果特征对应于AAA列空间中最大奇异值方向,而提示调优通过抑制与较小奇异值相关的扰动敏感方向(即,抑制虚假特征)来增强鲁棒性。通过视觉提示,因果特征得到加强,导致矩阵AAA的SVD逐渐满足Σc⊥→0\Sigma_{c^{\perp}}\rightarrow0Σc⊥→0,只留下σ1,...,σk\sigma_{1},\ldots,\sigma_{k}σ1,...,σk。此时V=VcV=V_{c}V=Vc,注意力更新简化为:
AV=(UcΣcVc⊤)V=UcΣc=∑i=1kσiui,A V=(U_{c}\Sigma_{c}V_{c}^{\top})V=U_{c}\Sigma_{c}=\sum_{i=1}^{k}\sigma_{i}u_{i},AV=(UcΣcVc⊤)V=UcΣc=i=1∑kσiui,
理想目标和条件。在概率术语中,我们的优化旨在满足以下理想恒等式:
Ez∼P(z)[f(X,z)] = ∑i=1kui σi.\mathbb{E}{z\sim P(z)}\big[f(X,z)\big]\;=\;\sum{i=1}^{k}u_{i}\,\sigma_{i}.Ez∼P(z)[f(X,z)]=i=1∑kuiσi.
在理论条件下,即学习表示与因果子空间同构,即模型完美地将UiU_iUi与捕获因果特征的前kkk个奇异方向对齐,这个等式成立。在实践中,我们优化以实现这一等式。这里,ZZZ表示混杂空间,zzz表示单个混杂因素。在此记法下,公式Eq. (3){\mathrm{Eq.~}}(3)Eq. (3)中的后门调整可以重写为:
P(y^∣do(X)) = Ez∼P(z) ⌈ P(y^∣X,z) ⌉ = Ez∼P(z) ⌈ f(X,z) ⌉ .P({\hat{y}}\mid d o(X))\;=\;\operatorname{\mathbb{E}}{z\sim P(z)}\!\left\lceil\,P({\hat{y}}\mid X,z)\,\right\rceil\;=\;\operatorname{\mathbb{E}}{z\sim P(z)}\!\left\lceil\,f(X,z)\,\right\rceil\!.P(y^∣do(X))=Ez∼P(z)⌈P(y^∣X,z)⌉=Ez∼P(z)⌈f(X,z)⌉.
当f(X,zi)=ui (see Eq. (7)f(X,z_{i})=u_{i}\:({\mathrm{see}}\:{\mathrm{Eq.}}\:(7)f(X,zi)=ui(seeEq.(7))时,同构成立。当学习的提示方向跨越混杂空间Z\mathcal{Z}Z时,提示和图像特征之间的交叉注意力实现了do(z)\mathrm{do}(z)do(z)算子:提示提供方向,而交叉注意力权重控制特征分量,抑制与非因果zzz变化对齐的那些分量,并驱动相应的奇异值趋向零(σk+1,...,σT→0)(\sigma_{k+1},\ldots,\sigma_{T}\rightarrow0)(σk+1,...,σT→0)。
在冻结骨干网络的视觉提示学习下,交叉注意力通过两种关键机制实现与因果干预的统计等价:主导奇异向量{u1,...,uk}\{u_{1},...,u_{k}\}{u1,...,uk}跨越捕获因果特征的低维子空间,而较小的OiO_iOi(与zk+1,...,zTz_{k+1},...,z_Tzk+1,...,zT相关)编码混杂噪声。通过优化提示以最大化∑i=1kσi2\textstyle\sum_{i=1}^{k}\sigma_{i}^{2}∑i=1kσi2,交叉注意力抑制混杂方向{uk+1,...,uT}\{u_{k+1},...,u_{T}\}{uk+1,...,uT},有效执行do(zi=0)\mathrm{do}(z_{i}=0)do(zi=0)对于i>ki>ki>k。这为可解释的域泛化提供了统一的理论框架:交叉注意力充当后门调整,解耦ZZZ诱导的虚假相关性。
4.2 双分支适配器
一方面,提示需要包含所有混杂因素ziz_izi。另一方面,与少样本跨域目标检测(CD-FSOD[2])相比,SDGOD方法面临更严峻的挑战,因为完全没有目标域数据,这严重限制了视觉提示的性能提升。如表1所示,SDGOD在NC上仅实现+ 2.6%+\!2.6\%+2.6%的改进,而在1-shot下为+4.1%。这突显了在零样本任务中需要额外适配器来缩小泛化差距。为解决这个问题,我们提出了双分支适配器(见图3)。
因果分支 专注于局部空间模式和因果语义。它使用MLP将交叉注意力视觉提示激活(由交叉注意力提示(CAP)生成)映射到因果特征。让p~i=CAP(pi\tilde{p}{i}=\mathrm{CAP}(p{i}p~i=CAP(pi)表示从原始提示参数pip_ipi和图像特征XXX获得的激活。映射形式化为
yi = σ (MLP(p~i)) ,y_{i}\;=\;\sigma\!\left(\mathrm{MLP}(\tilde{p}_{i})\right)\!,yi=σ(MLP(p~i)),
其中ooo是按元素应用的sigmoid函数,因此yi∈[0,1]d.y_{i}\in\lbrack0,1]^{d}.yi∈[0,1]d.
辅助分支 利用傅里叶分析。它通过关注相位信息或过滤幅度来提取域不变特征。这种方法,正如Yang等人[38]所建议的,隔离稳定结构免受域特定伪影影响。我们应用傅里叶变换来抑制域依赖扰动。具体来说,我们使用具有傅里叶变换的瓶颈MLP。对于输入ttt xi.x_{i}.xi.,过程是:
xi=σ(Wup⋅Wdown(xi)),xi=F−1(MASK⋅F(xi)).\begin{aligned}{x_{i}}&{{}=\sigma(W_{u p}\cdot W_{d o w n}(x_{i})),}\\ {x_{i}}&{{}=\mathcal{F}^{-1}(\mathrm{MASK}\cdot\mathcal{F}(x_{i})).}\end{aligned}xixi=σ(Wup⋅Wdown(xi)),=F−1(MASK⋅F(xi)).
Wdown∈RD×rW_{d o w n}\in\mathbb{R}^{D\times r}Wdown∈RD×r和Wup∈Rr×DW_{u p}\in\mathbb{R}^{r\times D}Wup∈Rr×D(其中DDD是通道维度,r=D16⟩\begin{array}{r}{r=\frac{D}{16}\rangle}\end{array}r=16D⟩)用于压缩特征维度。傅里叶变换F\mathcal{F}F及其逆F−1\mathcal{F}^{-1}F−1将特征分解为频率分量;然后在频域中应用高通掩码(MASK)以提取高频表示。这个分支在频域中操作,检测混杂因素如颜色偏移和背景图案。正如Zhang等人[39]提出的,我们的傅里叶分支充当虚假特征的无监督检测器,过滤掉域特定噪声。在训练期间,网络学会忽略这些分量,因为主分支和分类器优先考虑稳定的、语义信号(更多细节见附录D)。因此,辅助分支通过在频域中隔离混杂因素来隐式识别它们。
5 实验
5.1 设置
数据集。 我们的实验数据集主要遵循SDGOD基准[3],涵盖五种不同的天气条件:白天晴朗(DC)、白天雾天(DF)、黄昏雨天(DR)、夜晚雨天(NR)和夜晚晴朗(NC)。数据集包含七个类别:公交车、自行车、汽车、摩托车(Mot.)、行人(Per.)、骑手(Rid.)和卡车(Tru.),这些类别分为:重型车辆(Hev.: 公交车, 卡车)、中型车辆(Mid: 汽车, 摩托车)和非机动车(Non: 自行车, 行人, 骑手)。"All"指标表示所有类别的平均精度。为了评估泛化能力,我们将评估扩展到Cityscapes-C[40],这是一个包含15种腐败类型(噪声、模糊、天气、数字)的基准,每种有五个严重程度级别。我们报告平均腐败性能(mPC)[40]来评估模型对分布外偏移的鲁棒性。所有腐败模式(如运动模糊、雪)都被排除在训练之外。
实现细节。 我们的模型采用DINO[23]和FasterRCNN[7]作为检测头。我们用预训练权重替换默认骨干网络,并使用AdamW优化器( 1×10−4, β1ˉ=0.9, β2=0.999ˉ(\,1\times10^{-4},\,\bar{\beta_{1}}=0.9,\,\beta_{2}=\bar{0.999}(1×10−4,β1ˉ=0.9,β2=0.999ˉ ',权重衰减10−4)10^{-4})10−4)训练所有模型12个周期。基础学习率设置为10−410^{-4}10−4,对象查询参考点和采样偏移使用0.1降低率的线性投影。实验在8个NVIDIA RTX 4090 GPU上进行,DINO[23]的批量大小为16,FasterRCNN为64。DINOv2冻结所有参数。我们采用平均精度(mAP@0.5 IoU)作为主要指标,与最先进的(SOTA)单域泛化方法进行基准测试:CDSD[3], ClipGAP[13], G-NAS[8], SRCD[9]。使用Cityscapes-C[40]进一步评估域鲁棒性,其中包括15种合成腐败(噪声、模糊、天气、数字)跨越五个严重程度级别。
5.2 与SOTA在SDGOD上的比较
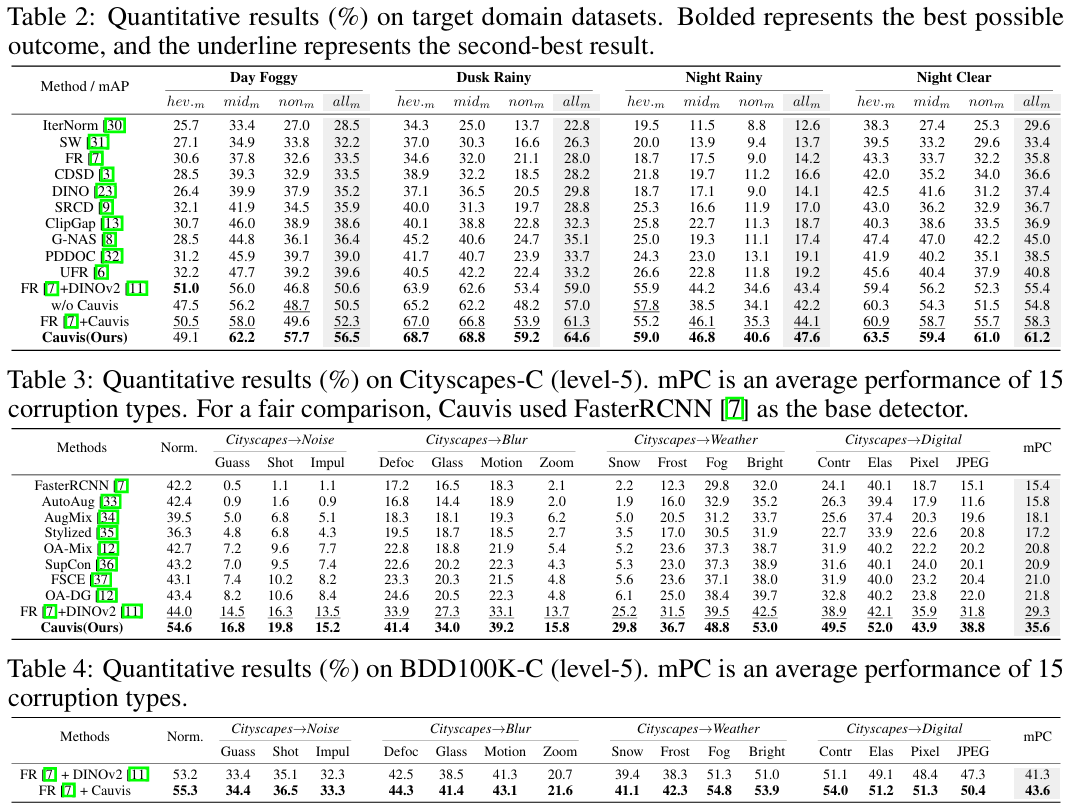
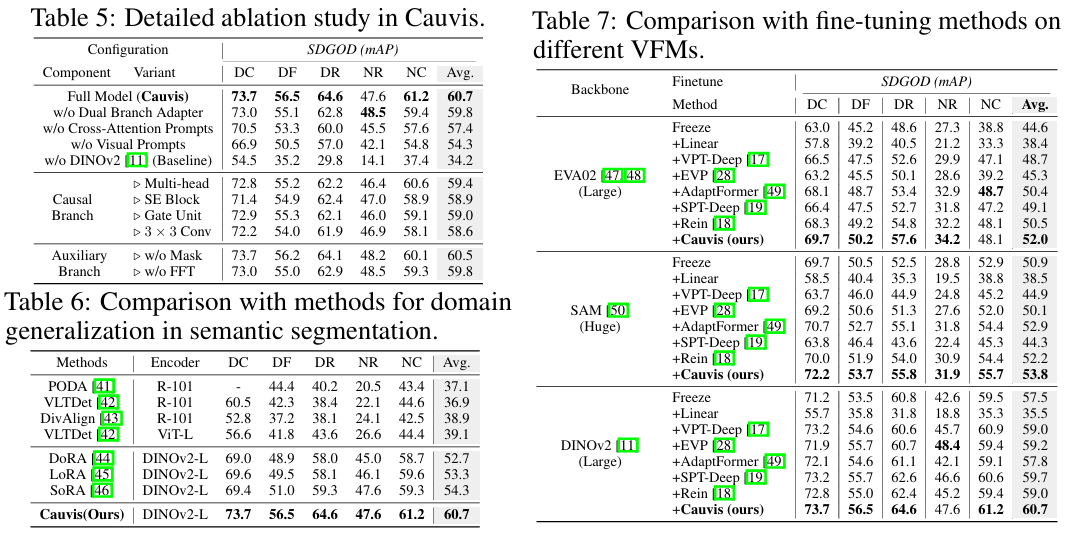
目标域上的结果。 表7总结了四个目标场景(白天雾天、黄昏雨天、夜晚雨天、夜晚晴朗)在三个类别划分(重型/中型/非机动车)和总体得分allmall_mallm上的结果。在所有配置中,Cauvis在几乎所有单元格中都达到最好或第二好的结果,并在每个场景中始终获得最高的allmall_mallm,优于强大的单域基线,如PDDOC[32]和UFR[6]。随着分布偏移加剧,优势变得更大:在恶劣天气下,Cauvis在白天雾天上超越UFR 16.9 mAP,在黄昏雨天上超越31.41 mAP(allmall_mallm),同时在所有条件下领先重型车辆划分。重要的是,增益不仅限于极端情况------Cauvis还改进了中型和非机动车划分------表明学习的表示是稳定和域不变的,而不是过度拟合严重腐败。消融实验("w/o Cauvis"和FR+DINOv2\mathrm{FR}+\mathrm{DINOv}2FR+DINOv2[11])进一步证实了这些发现:移除我们的组件会降低性能,而在FR+DINOv2\mathrm{FR}+\mathrm{DINOv2}FR+DINOv2[11]上添加Cauvis会产生额外增益,证实了交叉注意力提示(抑制虚假线索)和基于傅里叶的辅助分支(保留高频、域不变结构)的互补作用。源域上的结果可在附录B中找到。
与SOTA方法比较。 在表7中,Cauvis在三个VFM上展示了对视觉提示方法(VPT[17], EVP[28], SPT[19])的一致优势,平均mAP改进分别为4.6%、4.0%和4.5%。Cauvis在所有三个VFM上保持对Rein[18]的明显优势,验证了其有效性。
5.3 在腐败基准上的鲁棒性(Cityscapes-C & BDD100K-C)
Cityscapes-C。 为了系统评估Cauvis的鲁棒性,我们在Cityscapes-C[40]上进行目标检测评估。如表3详细所示,Cauvis在mPC上比先前SOTA方法[12]提高了13.8%。Cauvis在所有15种腐败类型上都超过OA-DG[12]。最显著的改进出现在与天气相关的扭曲中,特别是在雪腐败上,与之前方法相比,mPC提高了23.7%。此外,报告了Faster R-CNN[7]与DINOv2[11]结合的性能比较。观察到Cauvis的mPC提高了6.3。这表明我们的方法可以显著提高模型的鲁棒性,而不仅仅是依靠VFM的先验知识来获得性能增益。
BDD100K-C。 表4显示,Cauvis在更多样化的现实世界腐败套件上也产生了一致的改进。为了公平,使用相同的检测器和骨干网络。Cauvis将mPC从41.3提高到43.6(+2.3),增益分布在噪声、模糊、天气和数字腐败上。这种跨数据集鲁棒性证实了我们因果提示和频域辅助分支的一般性。
5.4 消融研究
整体设计的消融。 我们的层次消融(表5)验证了双分支设计的必要性:移除此模块会导致性能降低0.9%。用元素级加法替换交叉注意力会使精度下降2.4%,确认了其在因果特征优化中的作用。对模型性能最大的贡献是使用DINOv2[23]作为骨干网络,这使平均性能降低了23.2%。移除傅里叶导致0.9% mAP损失,证明了其在抑制域噪声方面的有效性。在因果分支中引入复杂设计[51, 52]并未导致精度增加,从而验证了我们模块化设计的有效性。
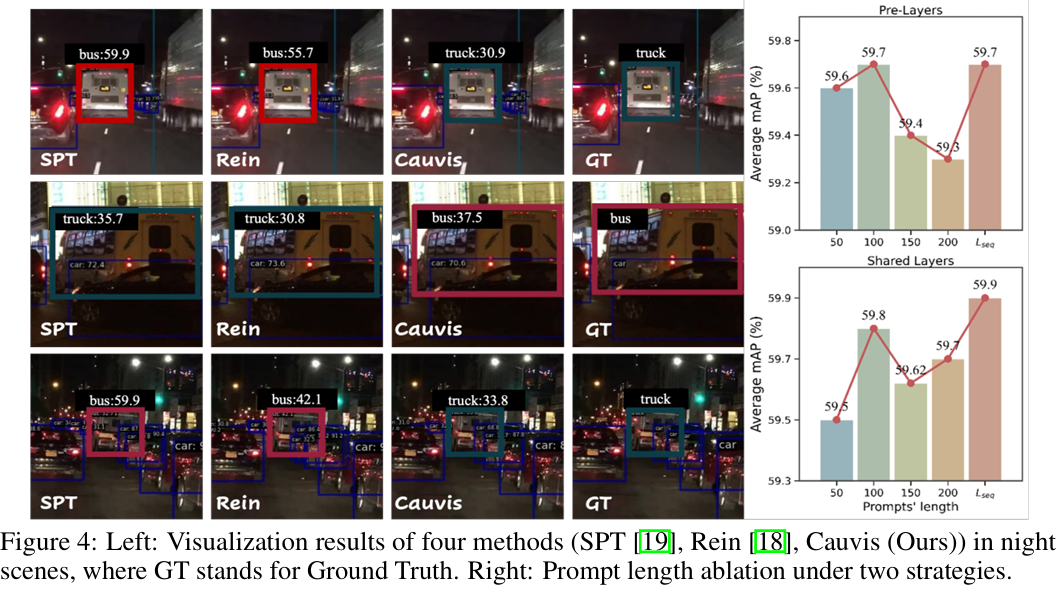
提示长度。 如图4(右)所示,约100个令牌的长度提供了近乎最优的权衡:对于分层变体达到59.7% mAP,对于共享变体达到59.8%。使用序列对齐长度Lseq (e.g., ≈ 1600L_{\mathrm{seq}}~(\mathrm{e.g.},\,\approx\,1600Lseq (e.g.,≈1600令牌)在理论上获得最佳数字(高达59.9%),但与100个令牌相比增益微乎其微(≤0.2点),而内存和计算成本却大幅增加,使训练不稳定且收敛变慢。因此,从训练角度来看,我们推荐100作为默认提示长度;然而,为了完整性和报告峰值性能,我们也包括了最长序列LseqL_{\mathrm{seq}}Lseq的结果。
可视化结果。 如图4所示,我们在夜间场景中对Cauvis和现有PEFT方法进行了视觉比较。在以白色公交车为主导的驾驶场景中,参数高效微调(PEFT)方法(如SPT[19], Rein[18])在关键分类特征缺失时表现出虚假相关性偏差。一个尺寸类似卡车的白色公交车被所有比较方法误分类为"卡车"(图4,第1列)。这种视觉模糊促使比较模型依赖表面线索(如颜色)而非语义特征。我们的方法将分类权重从基于颜色的虚假相关性转移到结构判别器(如高频几何轮廓)。
6 结论
在本文中,我们提出了Cauvis,一种用于单源域泛化目标检测的方法,可以缓解虚假相关性。从因果建模的角度,Cauvis将视觉提示与交叉注意力集成,实现隐式后门调整。为了从域特定噪声中分离因果信号,我们引入了双分支适配器:一个基于傅里叶的分支,提取高频、域不变特征,以及一个因果对齐的提示投影,抑制混杂因素。在多个基准上的大量实验显示了相对于最先进基线的一致增益,消融研究验证了每个组件的贡献。总体而言,这项工作通过统一因果推断与基于提示的建模,推进了单源域泛化。
致谢
本工作得到了中国国家自然科学基金(62376252);浙江省领军雁计划(2025C02025,2025C01056);以及中国湖北省自然科学基金(No.2022CFA055)的支持。