目录
[一、盛最多水的容器(LeetCode 11)](#一、盛最多水的容器(LeetCode 11))
[1. 题目描述](#1. 题目描述)
[2. 核心分析](#2. 核心分析)
[3. 完整代码](#3. 完整代码)
[4. 关键细节 & 易错点](#4. 关键细节 & 易错点)
[二、接雨水(LeetCode 42)](#二、接雨水(LeetCode 42))
[1. 题目描述](#1. 题目描述)
[2. 核心分析](#2. 核心分析)
[3. 完整代码](#3. 完整代码)
[4. 关键细节 & 易错点](#4. 关键细节 & 易错点)
前言
"盛最多水的容器"(LeetCode 11)和 "接雨水"(LeetCode 42)是算法面试中双指针法的高频考题,两者均围绕 "柱子高度数组" 展开,核心都是利用「数组线性有序」的特性,通过双指针移动缩小遍历范围,将暴力 O (n²) 复杂度优化为 O (n)。
一、盛最多水的容器(LeetCode 11)
1. 题目描述
给定一个长度为 n 的整数数组 height,数组中的每个元素代表垂直方向的柱子高度,柱子之间的间距为 1。请找出两根柱子,使得它们与 x 轴共同构成的容器能容纳最多的水,返回最大容积。
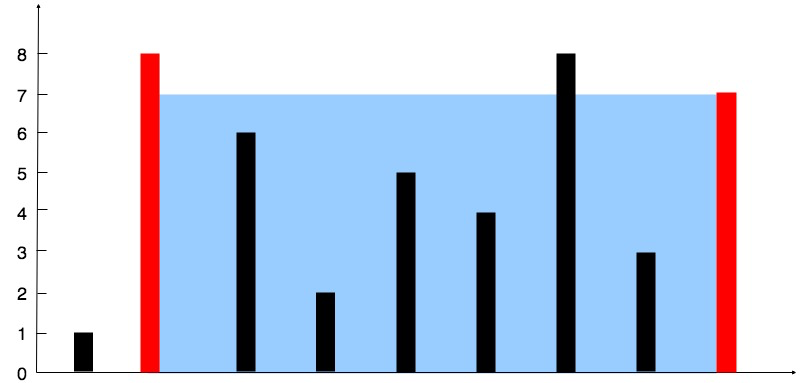
示例:输入:
height = [1,8,6,2,5,4,8,3,7]输出:49(选择索引 1 的 8 和索引 8 的 7,宽度 7,高度 7,容积 7×7=49)
2. 核心分析
(1)问题本质
容器的容积由两个因素决定:
- 宽度:两根柱子的索引差
right - left; - 高度:两根柱子中较矮的那根 (水的高度无法超过矮柱)。容积公式:
area = (right - left) × min(height[left], height[right])。
(2)暴力解法的问题
暴力法遍历所有柱子对 (i,j),计算每对的容积并取最大值,时间复杂度 O (n²),当 n 较大时会超时。
(3)双指针优化思路
核心逻辑:谁矮移谁。
- 初始状态:左指针
left指向数组头部(0),右指针right指向数组尾部(n-1),此时宽度最大; - 指针移动依据:
- 若
height[left] < height[right]:移动左指针(left++)。因为此时容积由左柱高度决定,若移动右指针,宽度减小,而高度最多还是左柱高度,容积必然更小; - 若
height[left] >= height[right]:移动右指针(right--)。同理,容积由右柱高度决定,移动左指针无意义;
- 若
- 每移动一次指针,计算当前容积,更新最大容积。
3. 完整代码(Java,带详细注释)
java
class Solution {
public int maxArea(int[] height) {
// 初始化最大容积为0
int maxArea = 0;
// 左指针:数组头部
int left = 0;
// 右指针:数组尾部
int right = height.length - 1;
// 指针相遇时停止遍历(宽度为0,无意义)
while (left < right) {
// 计算当前宽度:右指针 - 左指针
int width = right - left;
// 计算当前高度:取左右柱子的较小值
int curHeight = Math.min(height[left], height[right]);
// 计算当前容积
int curArea = width * curHeight;
// 更新最大容积
maxArea = Math.max(maxArea, curArea);
// 核心:谁矮移谁
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return maxArea;
}
}4. 关键细节 & 易错点
- 指针终止条件:
left < right(而非left <= right),因为left == right时宽度为 0,容积为 0; - 移动指针的依据是「柱子高度」,而非「当前容积」,避免错误移动高指针;
- 无需处理重复高度:即使相邻柱子高度相同,按规则移动即可,不会遗漏最大容积(重复高度不影响 "谁矮移谁" 的核心逻辑)。
二、接雨水(LeetCode 42)
1. 题目描述
给定 n 个非负整数表示每个柱子的高度,计算按此排列的柱子,下雨之后能接多少雨水。

示例:输入:
height = [0,1,0,2,1,0,1,3,2,1,2,1]输出:6(蓝色部分为雨水,总量 6)
2. 核心分析
(1)问题本质
每个位置能接住的雨水量由「左右两侧的最大高度」决定:
- 某位置
i的雨水量 =min(左侧最大高度, 右侧最大高度) - height[i]; - 若结果为负数,说明该位置无法接水(高度高于两侧最大高度),取 0。
(2)暴力解法的问题
暴力法对每个位置,分别计算左侧最大高度和右侧最大高度,时间复杂度 O (n²),超时风险高。
(3)双指针优化思路
核心逻辑:谁的最大高度小,移谁。
- 初始化:左指针
left指向头部(0),右指针right指向尾部(n-1);维护leftMax(左侧最大高度)、rightMax(右侧最大高度); - 指针移动依据:
- 若
leftMax < rightMax:处理左指针位置(雨水量由leftMax决定),计算该位置雨水量,左指针右移,并更新leftMax; - 若
leftMax >= rightMax:处理右指针位置(雨水量由rightMax决定),计算该位置雨水量,右指针左移,并更新rightMax;
- 若
- 累加所有位置的雨水量,得到总和。
3. 完整代码(Java,带详细注释)
java
class Solution {
public int trap(int[] height) {
// 总雨水量
int totalWater = 0;
// 左指针:数组头部
int left = 0;
// 右指针:数组尾部
int right = height.length - 1;
// 左侧最大高度(初始为左指针位置的高度)
int leftMax = 0;
// 右侧最大高度(初始为右指针位置的高度)
int rightMax = 0;
while (left <= right) {
// 核心:谁的最大高度小,处理谁的位置
if (leftMax < rightMax) {
// 更新左侧最大高度(当前左指针高度可能更大)
leftMax = Math.max(leftMax, height[left]);
// 计算左指针位置的雨水量(负数则取0)
int curWater = leftMax - height[left];
totalWater += Math.max(curWater, 0);
// 左指针右移
left++;
} else {
// 更新右侧最大高度
rightMax = Math.max(rightMax, height[right]);
// 计算右指针位置的雨水量
int curWater = rightMax - height[right];
totalWater += Math.max(curWater, 0);
// 右指针左移
right--;
}
}
return totalWater;
}
}4. 关键细节 & 易错点
- 指针终止条件:
left <= right(需处理所有位置,包括left == right); - 先更新最大高度,再计算雨水量:避免用 "旧的最大高度" 计算(比如左指针右移后,新位置的高度可能超过原
leftMax); - 雨水量需取非负:若
leftMax - height[left] < 0,说明该位置无雨水,累加 0 即可。
三、两道题核心对比(复习重点)
| 维度 | 盛最多水的容器 | 接雨水 |
|---|---|---|
| 问题目标 | 找「单次最优」的容器容积(最大值) | 求「所有位置」的雨水总和(累加值) |
| 双指针移动依据 | 谁矮移谁(基于当前柱子高度) | 谁的最大高度小,移谁(基于左右最大高度) |
| 核心计算逻辑 | 宽度 × 最小高度(单次计算) | 最小最大高度 - 当前高度(累加计算) |
| 指针终止条件 | left < right | left <= right |
| 时间复杂度 | O(n) | O(n) |
| 核心易错点 | 错误移动高指针 | 未先更新最大高度就计算雨水量 |
四、总结
- 记住核心口诀:
- 盛水容器:宽乘矮,矮移动;
- 接雨水:比最值,小移动,算差值,累总和;
- 双指针的核心是 "移动指针的确定性"------ 确保移动后不会遗漏最优解 / 所有可能;
- 复现代码时,先写指针初始化→循环条件→核心计算→指针移动,再补细节(如更新最大值、累加值)。
