题目介绍
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?

提示:
1 <= n <= 45
cpp
class Solution {
public:
int climbStairs(int n) {
}
};原题链接: 70. 爬楼梯 - 力扣(LeetCode)
解析
1 . 本题需求很明确,但是初次接触这种类型的小伙伴知晓怎么自己推导答案,不知背后蕴藏的算法
2 . 它给的代码,参数只有 n 个阶梯,要求返回走到n个阶梯的方法
3 . 对于先走1步还是后走1步的方法,都是算作不同方法
4 . 这意味着,拿到一个要走到n级阶梯这个目标,每次出发都有两个选择:左一个是走1步,右一个是走2步
5 . 你能想到什么数据结构呢
递归------青春版
1 . 数组排除,链表也不行。都是顺序结构
2 . 非树型结构莫属,而且也只有两个分叉------摘下面具,就是最熟悉的二叉树
3 . 二叉树与递归就好比🐟和水
4 . 这棵二叉树的每个结点就是一步台阶或者两步台阶
5 . 再看递归------老两样,核心任务和递归出口
核心任务:确定当前树要完成的任务(往往结合参数和返回值设计)
递归出口:对传入的参数进行审判
核心任务a . 现在n就是当前树,表示现在已经走到n级台阶了,因为给的参数就是n
b . 核心任务就是计算当前树(台阶数)的方法数
c . 我们从n出发,接下来要么n-2 要么n-1 ------确定了左右子树
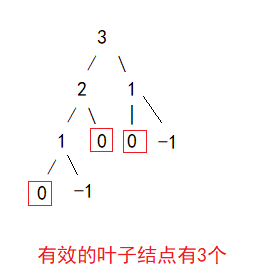
图1 举例
1)当2为当前树,计算出走到2的方法数;当1为当前树,计算出走到1台阶的方法数
2)当3为当前数,当前树的核心任务就是计算出走到3阶梯的方法数 = 左子树方法数 + 右子树的方法数
d . 当前树往往用当前结点表示,此处亦然。用当前走到的台阶表示
e . 需要再加个变量记录当前树的方法数否?不需要,返回值为int,直接返回就行
cpp
class Solution {
public:
int climbStairs(int n) {
return climbStairs(n-1)+climbStairs(n-2);// 核心任务,一步到位
}
};递归出口
a . 当向下走,不断走1步,或者走2步。
1)n == 0 说明这个方法可行,返回1
2)n < 0 说明这个方法不可行,返回0
注:所以说白:就是在计数整棵树有效的叶子结点。当叶子结点为0有效,向上开始返回1
当然这个认知,也是在从推导完核心任务和递归出口,自然而然得出的
完整参考代码:
cpp
class Solution {
public:
int climbStairs(int n) {
if(n == 0) return 1;
if(n < 0) return 0;
return climbStairs(n-1)+climbStairs(n-2);
}
};递归------工作留痕版
1 . 《递归------青春版》的方法,清晰明了------但一旦碰上n大的数,比如:44就会超过时间限制
2 . 难道有无用功出现吗
图3 无用功
a . 比如图上,我们会两次走到1这棵树,但是在1台阶的方法数都是左0右1,如果不拦着程序递归,它就会再去计算一遍1台阶的方法数
b . 有没有方法能让当前树如果遇到重复,就立马返回它曾经记录下的方法数
c . 不妨创建个备忘录数组
memo[n+1] 大小为n+1 。存储的元素为 对应阶梯的方法数
d . 因为备忘录数组需要初始化,那不妨把递归逻辑放在下层
cpp
class Solution {
public:
int _climbStairs(int n,vector<int>& memo)
{
}
int climbStairs(int n) {
vector<int> memo(n+1,-1);
return _climbStairs(n,memo);
}
};注:
1 . vector<int> memo(n+1,-1);初始化出n+1个格子,下标范围为0~n
2 . 格子里都初始化为-1
3 . 于是,递归逻辑里加上一本备忘录。记得传vector<int>& ,输出型参数的好处还记得否?减少拷贝,原地修改参数
cpp
int _climbStairs(int n,vector<int>& memo)
{
if(n == 0) return 1;
if(n < 0) return 0;
if(memo[n] != -1) return memo[n]; // 如果以前遇到过这个阶梯,掏出备忘录,直接返回当前结点的方法数
memo[n] = _climbStairs(n-1,memo)+_climbStairs(n-2,memo);// 先更新备忘录
return memo[n];// 再返回
}完整参考代码:
cpp
class Solution {
public:
int _climbStairs(int n,vector<int>& memo)
{
if(n == 0) return 1;
if(n < 0) return 0;
if(memo[n] != -1) return memo[n];
memo[n] = _climbStairs(n-1,memo)+_climbStairs(n-2,memo);
return memo[n];
}
int climbStairs(int n) {
vector<int> memo(n+1,-1);
return _climbStairs(n,memo);
}
};动态规划------自下而上
1 . 不要被"动态规划"唬住,先看我接下来怎么说,慢慢去感受"动态规划"
2 . 如果说递归是从第n节台阶不断往下走,每次走1步或者2步,最后遇到有效的结点才算一个方法
3 . 那么动态规划就是直接从底部出发,不断计算出 台阶2,3,4,5,6......的方法数
cpp
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n+1);// dp[i]表示i台阶的总方法数
dp[0] = 1;
dp[1] = 1;
for(int i = 2;i <= n;i++)
{
dp[i] = dp[i-1]+dp[i-2];// 这里不要迷糊,就是dp[i]就是dp[i-1]+dp[i-2]
}
return dp[n];
}
};注:
1 . dp[i]等于i-1台阶的方法数加上i-2的方法数
2 . 你可以在脑海里想象,我们i-1台阶的方法数就是i-1那棵树下所有的有效结点
3 . dp[i-2] 也是同样的道理
4 . 起点dp[0] 为1,不动 (这个比较特殊;dp[1]只有0->1一种方法
总结以及完整参考代码:
总结暂时放一下,博主赶个路😣
cpp
class Solution {
public:
int climbStairs(int n) {
if(n == 0) return 1;
if(n < 0) return 0;
return climbStairs(n-1)+climbStairs(n-2);
}
};
cpp
class Solution {
public:
int _climbStairs(int n,vector<int>& memo)
{
if(n == 0) return 1;
if(n < 0) return 0;
if(memo[n] != -1) return memo[n];
memo[n] = _climbStairs(n-1,memo)+_climbStairs(n-2,memo);
return memo[n];
}
int climbStairs(int n) {
vector<int> memo(n+1,-1);
return _climbStairs(n,memo);
}
};
cpp
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n+1);// dp[i]表示i台阶的总方法数
dp[0] = 1;
dp[1] = 1;
for(int i = 2;i <= n;i++)
{
dp[i] = dp[i-1]+dp[i-2];
}
return dp[n];
}
};
cpp
class Solution {
public:
void dfs(int n,int& way,vector<int>& memo)
{
if(n < 0) return;
if(n == 0) {
way++;
return;
}
if(memo[n]!=-1)
{
way += memo[n];
return;
}
int tmp = way;
dfs(n-2,way,memo);
dfs(n-1,way,memo);
memo[n] = way - tmp;
}
int climbStairs(int n) {
int way = 0;
vector<int> memo(n+1,-1);
dfs(n,way,memo);
return way;
}
};// 此方法其实是 工作留痕版------再加了个输出型参数,记录当前台阶的方法数way。
//于是就删掉了递归的返回值,通过way进行返回还有两篇,燥候------