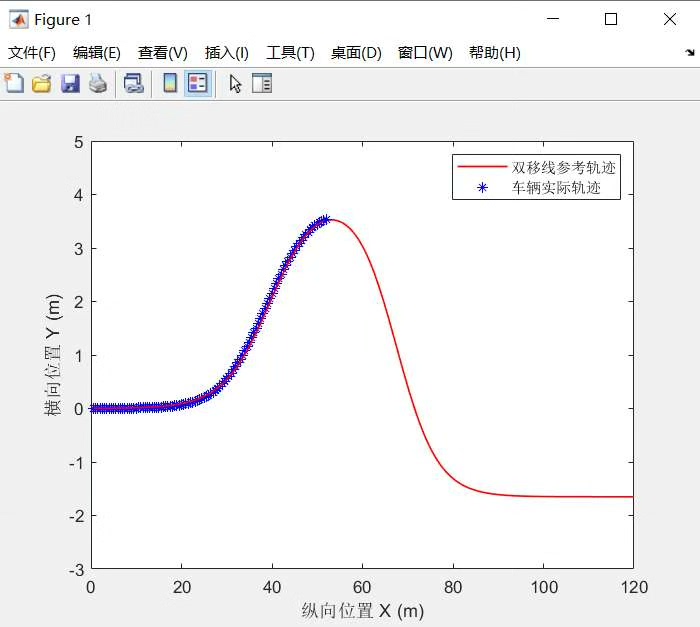
基于运动学模型的非线性模型预测控制轨迹跟踪纯代码版本：开启学习 NMPC 的奇妙之旅

基于运动学模型的非线性模型预测控制轨迹跟踪纯代码版本 1.实时的曲线跟踪动画 2.重要参数一键出图 3.详细的代码分区及重点注释进行了误差分析以及曲线对比，代码计算了横向跟踪误差最大值，横向跟踪误差均方根值 5.适合学习非线性模型预测控制(NMPC)、车辆运动学模型 6.可提供有偿 7.代码包含主函数.m文件，目标函数.m文件，运行时候，放置在同一路径，运行主函数文件就行

在自动驾驶和机器人运动控制领域，轨迹跟踪是一个至关重要的课题。今天要给大家分享的是基于运动学模型的非线性模型预测控制（NMPC）轨迹跟踪的纯代码版本，这个代码对于想要深入学习 NMPC 以及车辆运动学模型的小伙伴来说，简直是宝藏。

实时的曲线跟踪动画

实时的曲线跟踪动画能够让我们直观地看到车辆或者机器人是如何沿着预设轨迹行驶的。通过动画，我们可以实时观测到控制算法的效果，及时发现问题并进行调整。在代码实现中，我们可以利用一些绘图工具包，比如 Matlab 中的 plot 函数结合循环来实现实时更新绘图。

matlab 复制代码

% 假设已经有轨迹点的数组 x_trajectory 和 y_trajectory
figure;
hold on;
for i = 1:length(x_trajectory)
    plot(x_trajectory(1:i), y_trajectory(1:i), 'b'); % 蓝色线条实时绘制轨迹
    drawnow; % 强制 Matlab 立即更新绘图
end
hold off;

这段代码首先创建了一个绘图窗口，hold on 保证每次绘图不会覆盖之前的内容。在循环中，每次绘制当前已经行驶到的轨迹点，drawnow 则确保绘图实时更新，让我们能看到轨迹是逐步绘制出来的动态效果。

重要参数一键出图

一键出图功能方便我们对算法中的重要参数进行分析。比如在 NMPC 算法中，预测时域、控制时域等参数对控制效果有着关键影响。我们可以通过代码将这些参数与算法性能指标（如跟踪误差）的关系绘制出来。

matlab 复制代码

% 假设已经有不同预测时域值的数组 prediction_horizons
% 以及对应的横向跟踪误差数组 lateral_errors
figure;
plot(prediction_horizons, lateral_errors, 'ro -');
xlabel('Prediction Horizon');
ylabel('Lateral Tracking Error');
title('Relationship between Prediction Horizon and Lateral Tracking Error');

上述代码将预测时域与横向跟踪误差的关系绘制成图。plot 函数以红色圆圈和线条展示数据点和趋势，xlabel、ylabel 和 title 分别对坐标轴和图表标题进行标注，方便我们直观理解参数与误差之间的联系。

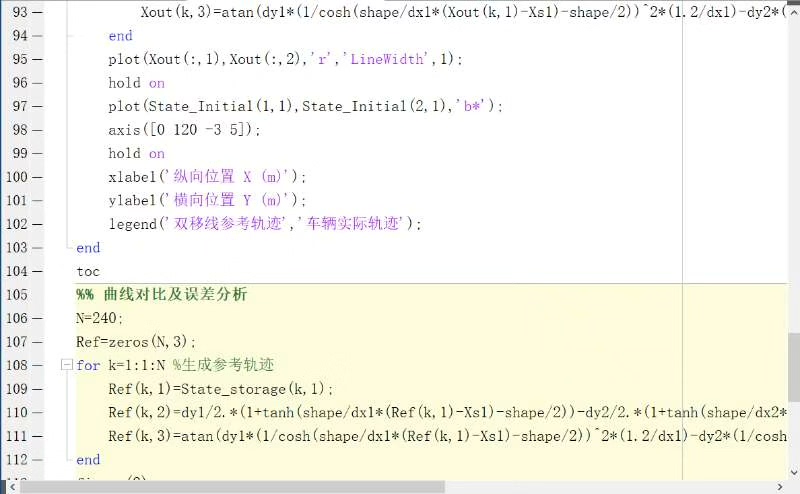
详细的代码分区及重点注释

为了方便大家理解代码逻辑，代码进行了详细的分区和重点注释。整个代码主要分为主函数和目标函数两部分，运行时，只需将主函数 .m 文件和目标函数 .m 文件放置在同一路径，运行主函数文件即可。

主函数部分

matlab 复制代码

% 主函数文件，运行整个轨迹跟踪算法
% 初始化参数
vehicle_params = initialize_vehicle_params(); % 初始化车辆参数
control_params = initialize_control_params(); % 初始化控制参数

% 获取参考轨迹
[x_ref, y_ref] = generate_reference_trajectory();

% 运行 NMPC 轨迹跟踪
[x_tracked, y_tracked] = run_nmpc_tracking(vehicle_params, control_params, x_ref, y_ref);

% 计算误差
[max_lateral_error, rms_lateral_error] = calculate_errors(x_ref, y_ref, x_tracked, y_tracked);

% 绘制结果
plot_results(x_ref, y_ref, x_tracked, y_tracked, max_lateral_error, rms_lateral_error);

在主函数中，首先初始化车辆参数和控制参数，然后生成参考轨迹。接着运行 NMPC 轨迹跟踪算法得到跟踪的轨迹，之后计算横向跟踪误差最大值和均方根值，最后绘制结果展示。

目标函数部分

matlab 复制代码

function cost = objective_function(u, state, ref_state, params)
% 目标函数计算成本值，用于 NMPC 优化
% u 是控制输入，state 是当前状态，ref_state 是参考状态，params 是参数结构体

% 提取参数
Q = params.Q; % 状态权重矩阵
R = params.R; % 控制输入权重矩阵

% 计算状态误差
state_error = state - ref_state;

% 计算成本
cost = state_error' * Q * state_error + u' * R * u;
end

目标函数在 NMPC 中用于计算成本值，以指导优化算法寻找最优的控制输入。这里通过状态误差和控制输入，结合权重矩阵来计算成本。

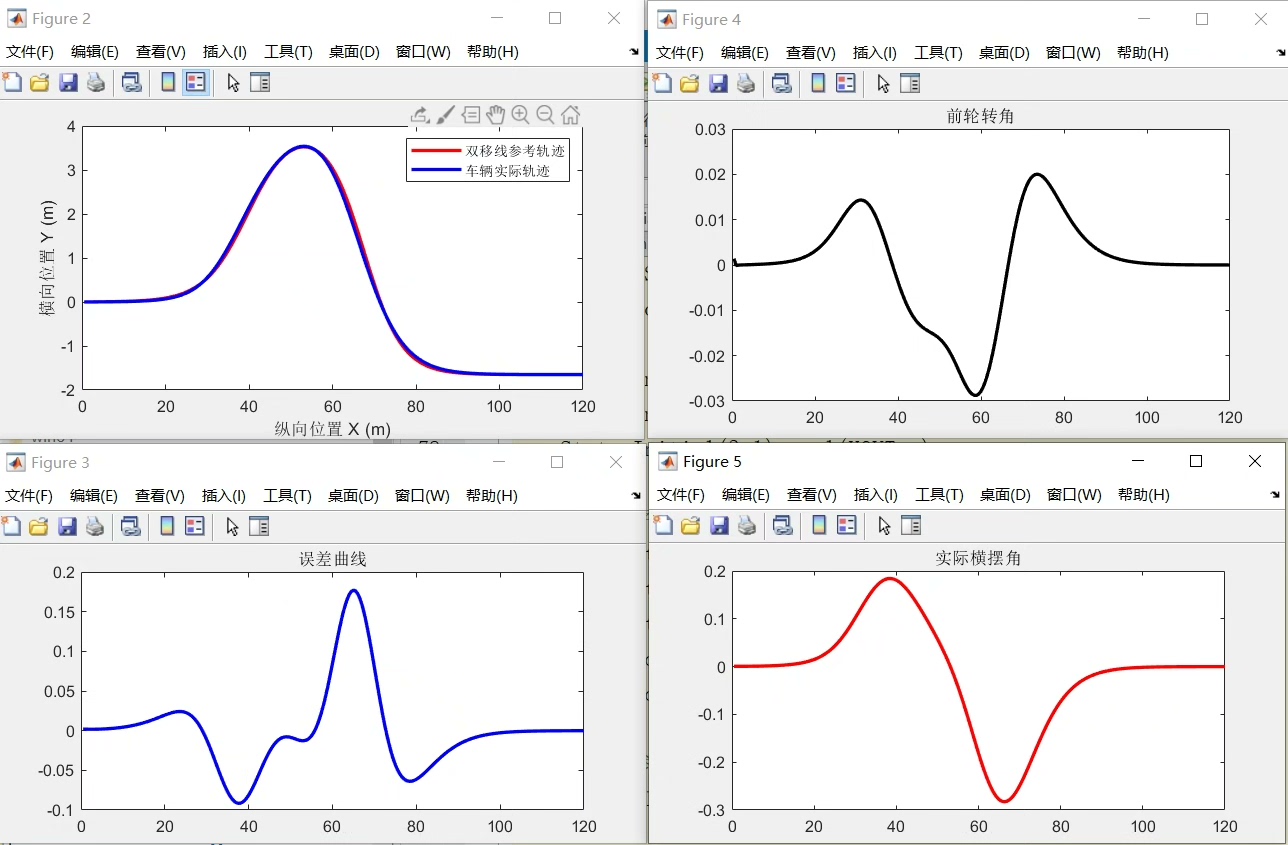
误差分析以及曲线对比

代码计算了横向跟踪误差最大值和横向跟踪误差均方根值，这两个指标能很好地衡量轨迹跟踪的性能。横向跟踪误差最大值反映了跟踪过程中出现的最大偏差，均方根值则综合考虑了整个跟踪过程中的误差情况，更全面地评估算法的准确性。

matlab 复制代码

function [max_error, rms_error] = calculate_errors(x_ref, y_ref, x_tracked, y_tracked)
% 计算横向跟踪误差最大值和均方根值
num_points = length(x_ref);
lateral_errors = zeros(num_points, 1);

for i = 1:num_points
    % 简单的横向误差计算，假设参考轨迹和跟踪轨迹点的 x 坐标对应
    lateral_errors(i) = abs(y_ref(i) - y_tracked(i));
end

max_error = max(lateral_errors);
rms_error = sqrt(mean(lateral_errors.^2));
end

这段代码遍历参考轨迹和跟踪轨迹的每个点，计算横向误差，然后得出最大值和均方根值。

总之，这份基于运动学模型的非线性模型预测控制轨迹跟踪代码，无论是对于学习 NMPC 和车辆运动学模型，还是实际应用中的算法开发，都具有很大的参考价值。如果有小伙伴对代码有进一步需求，可提供有偿服务哦。希望大家通过这份代码，在相关领域的学习和研究中取得更多收获！