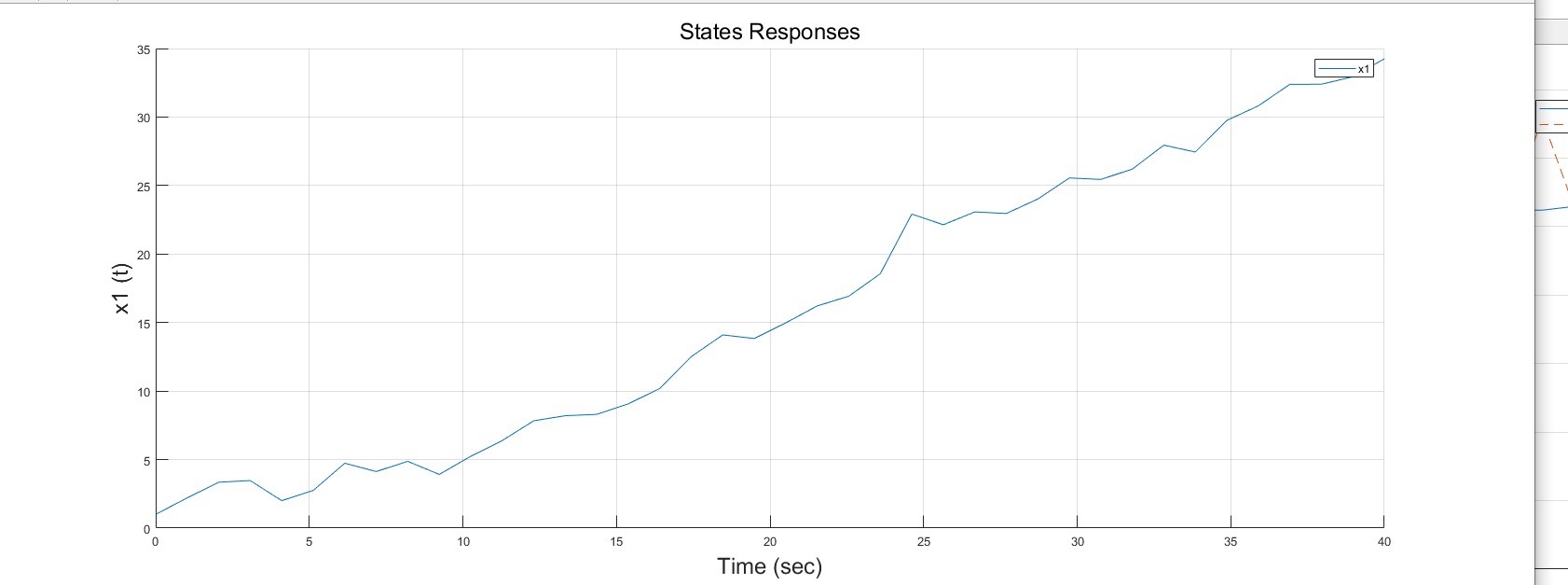
matlab环境下离散卡尔曼滤波器算法,用于消除传感器输出上的噪声。 可用于土木,航空航天和机械等领域。 本品为matlab程序,附带参考文献及算例。 算例可直接运行。
在土木、航空航天和机械等众多领域,传感器输出数据常常会受到噪声的干扰,这时候离散卡尔曼滤波器就派上大用场啦。今天咱就唠唠在Matlab环境下如何实现这个算法。
离散卡尔曼滤波器算法原理
简单来说,卡尔曼滤波器是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。对于离散系统,它主要分为预测和更新两个步骤。
预测步骤
预测状态:\\hat{x}*{k\|k - 1} = A\\hat{x}*{k - 1\|k - 1} + Bu_{k}
预测协方差:P*{k\|k - 1} = AP*{k - 1\|k - 1}A\^{T}+Q
这里,\\hat{x}*{k\|k - 1}是基于上一时刻估计值预测的当前状态,A是状态转移矩阵,B是控制矩阵,u*{k}是控制输入,P_{k\|k - 1}是预测协方差,Q是过程噪声协方差。
更新步骤
卡尔曼增益:K*{k} = P*{k\|k - 1}H\^{T}(HP_{k\|k - 1}H\^{T}+R)\^{-1}
更新状态估计:\\hat{x}*{k\|k} = \\hat{x}* {k\|k - 1}+K*{k}(z*{k}-H\\hat{x}_{k\|k - 1})
更新协方差:P*{k\|k}=(I - K*{k}H)P_{k\|k - 1}
其中,K*{k}是卡尔曼增益,H是观测矩阵,z* {k}是观测值,R是观测噪声协方差,\\hat{x}*{k\|k}是更新后的状态估计,P*{k\|k}是更新后的协方差。
Matlab代码实现
matlab
% 离散卡尔曼滤波器示例代码
% 初始化参数
A = 1; % 状态转移矩阵
H = 1; % 观测矩阵
Q = 0.01; % 过程噪声协方差
R = 0.1; % 观测噪声协方差
P = 1; % 初始协方差
x_hat = 0; % 初始状态估计
% 生成带有噪声的传感器数据
t = 0:0.1:10;
true_signal = sin(t);
noise = sqrt(R)*randn(size(t));
measured_signal = true_signal + noise;
for k = 1:length(t)
% 预测步骤
x_hat_minus = A * x_hat;
P_minus = A * P * A' + Q;
% 更新步骤
K = P_minus * H' / (H * P_minus * H' + R);
x_hat = x_hat_minus + K * (measured_signal(k) - H * x_hat_minus);
P = (1 - K * H) * P_minus;
% 存储滤波后的值
filtered_signal(k) = x_hat;
end
% 绘图
figure;
plot(t, true_signal, 'b', 'DisplayName', '真实信号');
hold on;
plot(t, measured_signal, 'r--', 'DisplayName', '带噪声信号');
plot(t, filtered_signal, 'g-.', 'DisplayName', '滤波后信号');
legend;
xlabel('时间 t');
ylabel('信号值');
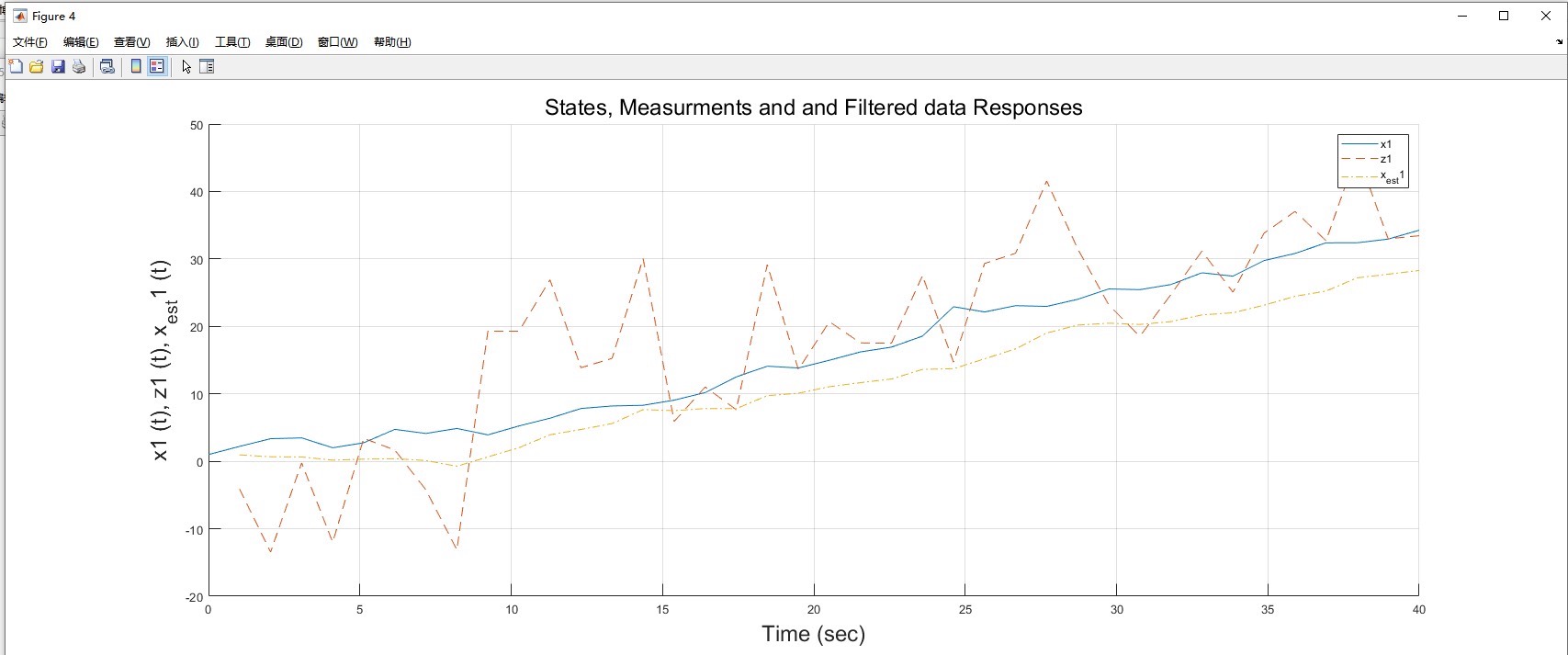
title('离散卡尔曼滤波器对传感器噪声的消除');代码分析
- 初始化部分 :设定了离散卡尔曼滤波器所需的各种参数,像状态转移矩阵
A、观测矩阵H等。同时初始化了状态估计x_hat和协方差P。 - 生成数据部分 :创建了一个时间序列
t,生成了真实信号truesignal*(这里用正弦函数举例),并加入了符合正态分布的噪声noise,得到了带有噪声的测量信号measured*signal。 - 循环部分 :按照离散卡尔曼滤波器的预测和更新步骤进行迭代计算。每一步都先进行预测,得到预测状态
xhatminus和预测协方差Pminus*,然后计算卡尔曼增益K,并更新状态估计x*hat和协方差P。最后将滤波后的信号值存储在filtered_signal中。 - 绘图部分 :用
plot函数将真实信号、带噪声信号和滤波后信号绘制在同一张图上,方便直观对比。
算例与参考文献
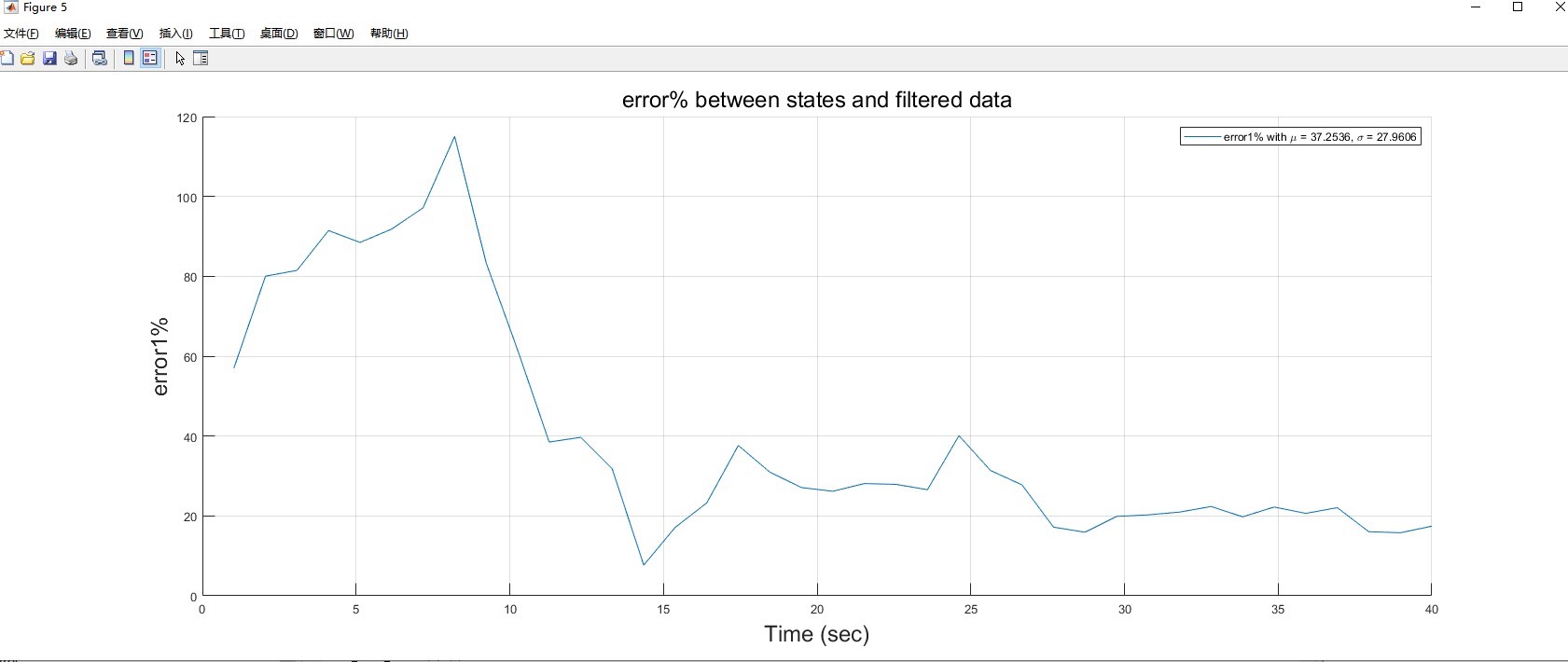
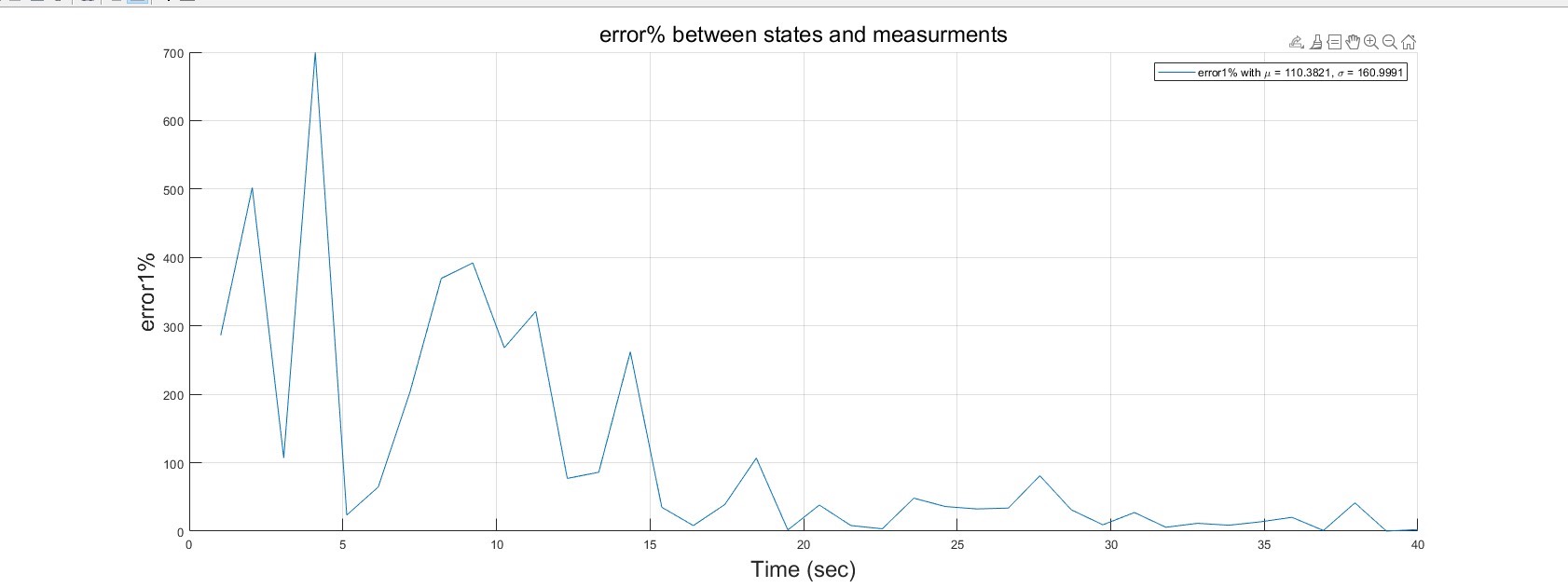
算例可以直接运行上述Matlab代码,就能看到离散卡尔曼滤波器对带有噪声的正弦信号的滤波效果。
参考文献[1]详细介绍了离散卡尔曼滤波器的理论基础,要是对算法原理还想深入研究,可以去瞅瞅。这里只是抛砖引玉,实际应用中可能需要根据具体的系统特性,仔细调整参数,以达到最佳的噪声消除效果。
1\] Maybeck, P. S. (1979). Stochastic models, estimation, and control (Vol. 1). Academic press. (这里参考文献只是示例,实际使用可替换为真实相关文献) 希望通过这个博文,能帮助大家在Matlab环境下快速上手离散卡尔曼滤波器,解决传感器噪声的烦恼。