遗传算法学习一之求函数的最值

前言

一、遗传算法简介

核心流程：

二、Matlab算法实现

[2.1 研究问题](#2.1 研究问题)

[2.2 确定适应度函数](#2.2 确定适应度函数)

[2.3 算法参数确定](#2.3 算法参数确定)

[2.4 算法实现](#2.4 算法实现)

[2.5 内容输出](#2.5 内容输出)

[2.6 完整代码](#2.6 完整代码)

三、结果分析

编辑

四、求最大值

[4.1 取反操作](#4.1 取反操作)

[4.2 分式操作](#4.2 分式操作)

总结

前言

初学遗传算法的话，感觉对算法的运行流程都能看得懂，但是对如何用代码实现这个流程比较疑惑，所以本章重点讲解使用Matlab代码实现的原理，会用到函数'optimoptions'和'ga'。只对算法进行实例化不含改进。

一、遗传算法简介

遗传算法（Genetic Algorithm, GA）是一种模拟自然选择和遗传机制的优化算法，属于进化计算的分支。通过模拟生物进化过程中的选择、交叉和变异操作，遗传算法能够在复杂搜索空间中高效寻找近似最优解，尤其适用于非线性、多峰或高维问题。

核心流程：

初始化种群**、**定义适应度函数、选择操作、交叉（重组）、变异操作、终止条件。

这里的每一步的解释大家可以去看算法介绍，每一步操作在生物学上的解释相信大家都能理解，简单来说就是依据达尔文进化论，一群种群在对环境有不同的适应能力（适应度），导致生存和繁衍的能力不同，多轮轮回后，得到了对环境适应度更高的种群。

等效于求函数的最大值，就是一群自变量对函数有不同的输出结果，设定输出越大的自变量适应度越高，通过选择和交叉来模拟生物的繁衍，多轮轮回后，得到了使函数到最大值的自变量。

理论我能知道，可是具体如何用代码实现呢？

二、Matlab算法实现

2.1 研究问题

先给出问题：

如下函数，请用遗传算法求出啊函数在[-10 10]区间上的最值。

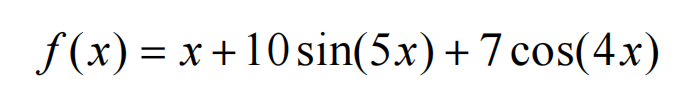
2.2 确定适应度函数

我们先设计适应度函数

Matlab 复制代码

%创建匿名函数
function y = fitness(x)
    y = x + 10*sin(5*x)+7*cos(4*x);
end
% 创建函数句柄
fun = @(x) fitness(x);
nVars = 1;

这里的自适应函数fitness就是我么要求的函数本身，这也是自适应函数最简单的设计之一。这可以保证函数输出和自适应度完美的同步变化。如果出现某个极值特别超群（超级个体）或者某区域的值都接近极值都需要对原函数进行尺度变换在充当自适应函数。

应为'ga'的目标函指定为函数句柄或函数名称，所以这里使用匿名函数创建函数句柄，nVars代表变量的数目。

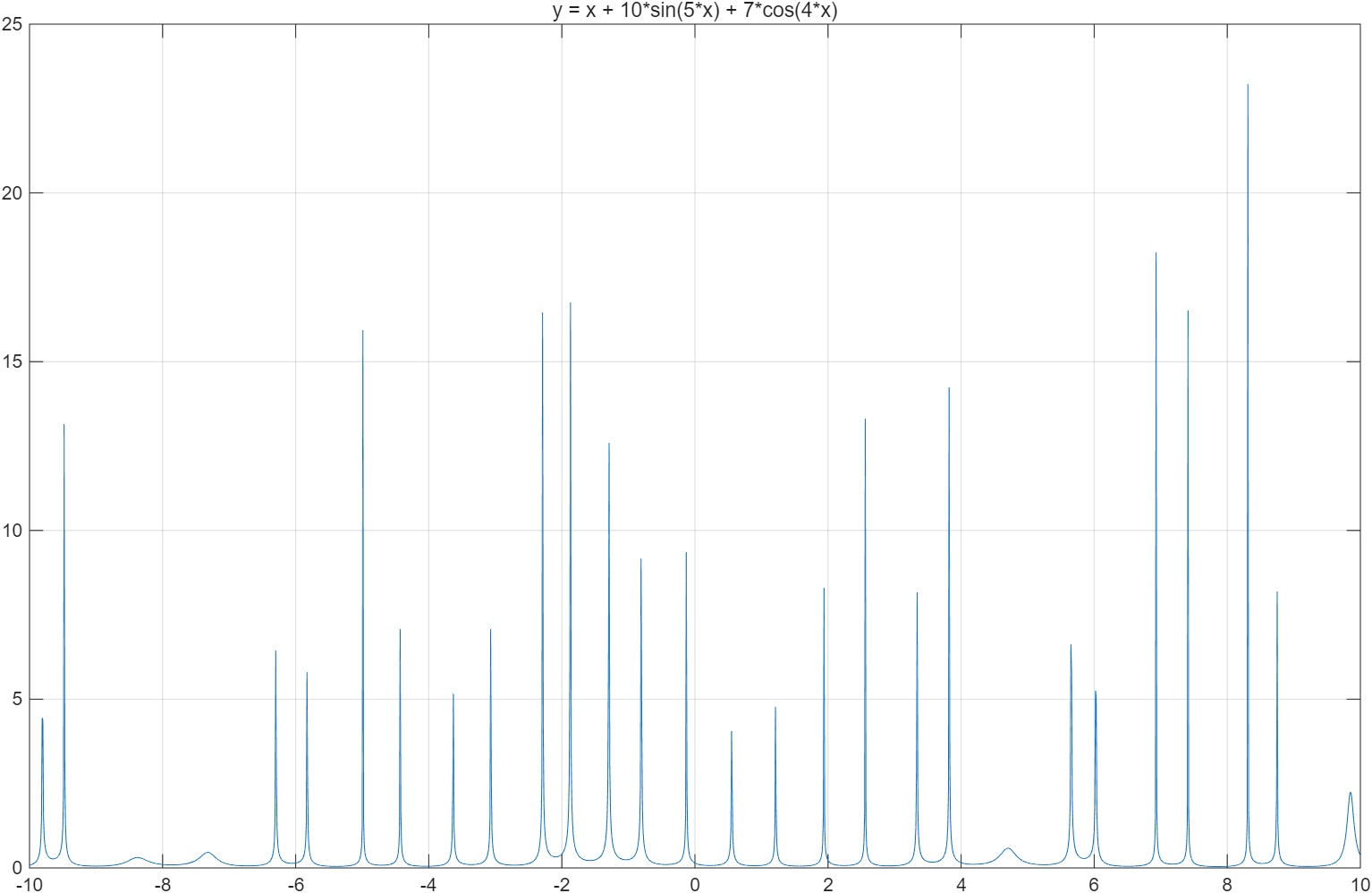
先生成原函数图像看一下，最小值大概在-5.3左右，最大值7.8左右。

Matlab 复制代码

%原函数图像
figure
x1 = -10:0.01:10;
plot(x1,fitness(x1));
title('y = x + 10*sin(5*x) + 7*cos(4*x)');
grid on;%添加网格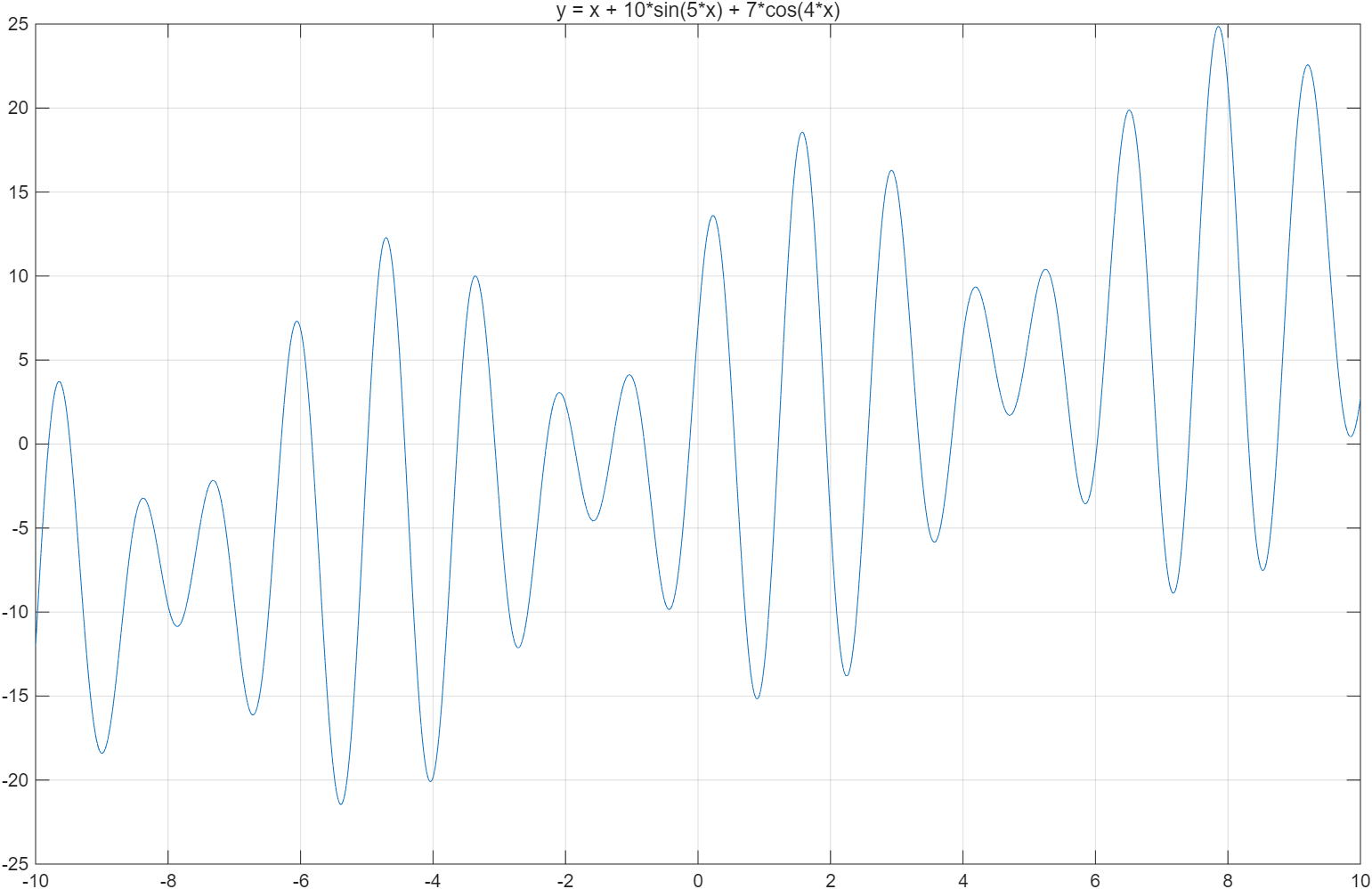

2.3 算法参数确定

接下来使用的optimoptions和ga函数归属 MathWorks 官方的特定工具箱Optimization Toolbox和Global Optimization Toolbox。2013b版本后都可以使用，我的版本是2025b，为了防止有些同学没有这个函数，我会上传到资源。

Matlab 复制代码

% 算法参数设置
options = optimoptions('ga', ...
    'MaxGenerations', 100, ...                  % 增大最大迭代次数（默认100）
    'PopulationSize', 100, ...                  % 增大种群大小（默认20）
    'MaxStallGenerations', 50, ...               % 配置停滞代数限制（默认值为50）
    'Display', 'iter', ...                      % 显示迭代过程，观察收敛趋势
    'PlotFcn', @gaplotbestf, ...                % 绘制每代最优值曲线，直观判断收敛
    'SelectionFcn',@selectionroulette, ...      % 轮盘赌选择策略，默认策略
    'CrossoverFcn',@crossoverscattered,...      % 是用于没有线性约束问题的默认交叉函数
    'MutationFcn',@mutationadaptfeasible,...    % 非整数约束时的默认突变函数，自适应变异，无需设置概率
    'FunctionTolerance', 1e-6, ...              % 目标函数容差（默认1e-4）
    'ConstraintTolerance', 1e-6);               % 约束容差（无约束时不生效）

ga函数的options指定为 optimoptions的输出或结构体，用来设置算法参数

第一个输入 'ga'：告诉 optimoptions，当前要配置的是「遗传算法求解器」的参数

后续的「名称 - 值对」：每一组 '参数名'，参数值对应一个算法配置项，参数名必须是求解器支持的官方字符串

... 是 MATLAB 的续行符，表示「本行代码未结束，下一行继续」

'MaxGenerations', 100：允许算法迭代最多 100 代，如果在ga函数因为达到MaxGenerations限制而停止，应该增大MaxGenerations值。

'PopulationSize', 100：每代种群包含 100 个「个体」，覆盖更多解空间，减少局部最优；若PopulationSize过小，种群丧失多样性，会把某个极值点当为最小点，也就是局部最优。

'MaxStallGenerations', 50：如果MaxStallGenerations代的最佳适应度函数值的平均相对变化小于或等于FunctionTolerance，则算法停止。

'Display', 'iter'：迭代过程中打印每代的最优值、平均适应度，实时监控收敛；其他的值含义如下：

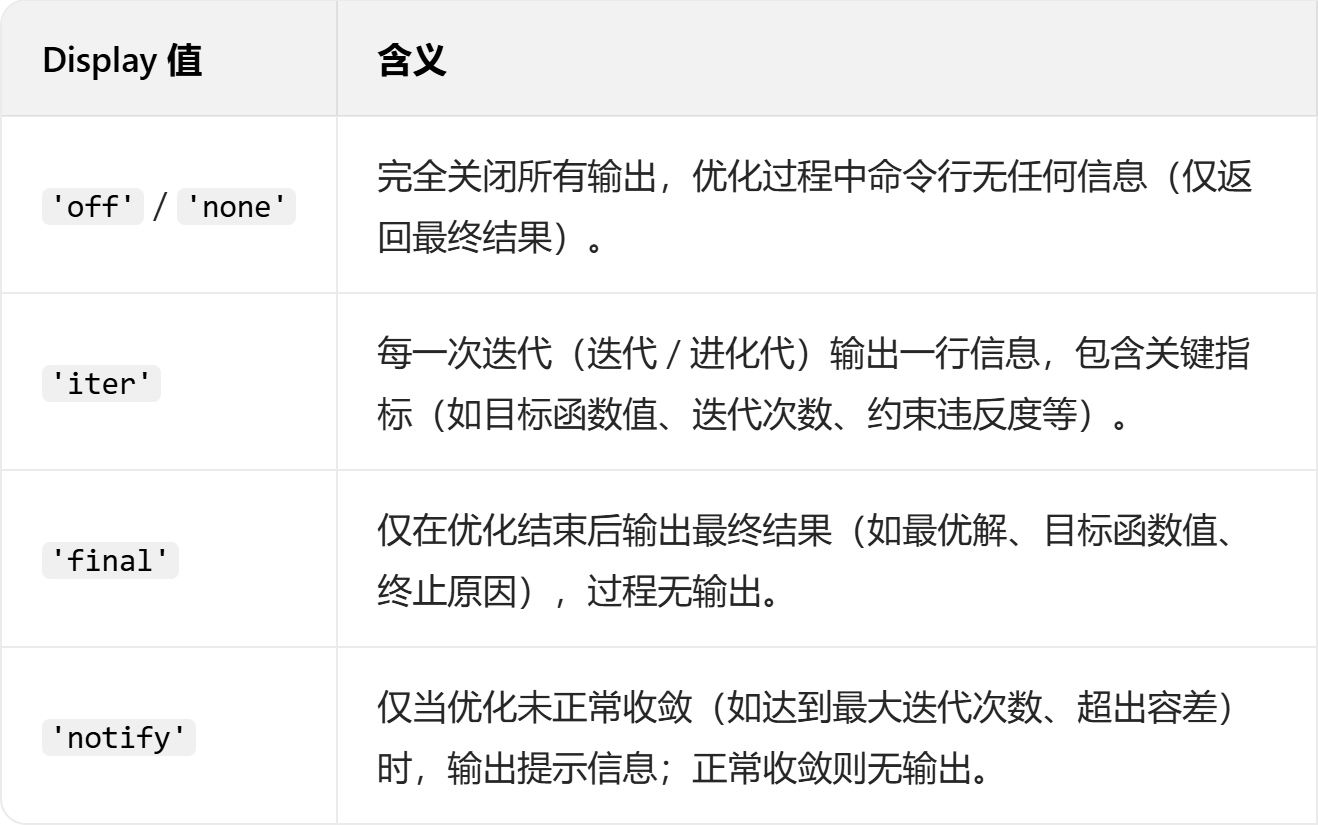
'PlotFcn', @gaplotbestf：PlotFcn 是核心可视化选项，@gaplotbestf是 MATLAB 内置的最优适应度绘图函数，二者结合的作用是在遗传算法迭代过程中，实时绘制并更新每一代的最优适应度值变化曲线

'SelectionFcn',@selectionroulette：轮盘赌选择策略，不配置时默认此策略，其他选择策略如下。

精英选择函数句柄：@selectionelite

锦标赛选择函数句柄：@selectiontournament

排序选择函数句柄：@selectionranking

'CrossoverFcn',@crossoverscattered：是用于没有线性约束问题的默认交叉函数

'MutationFcn',@mutationpower：非整数约束时的默认突变函数。

整数约束：要求优化变量的取值必须是整数（正整数 / 负整数 / 0），不允许小数 / 分数。

非整数约束：变量可取值为任意实数（小数、分数、整数均可），是优化的默认约束。

'FunctionTolerance', 1e-6：如果 MaxStallGenerations代的最佳适应度函数值的平均相对变化小于或等于 FunctionTolerance，则算法停止

'ConstraintTolerance', 1e-6 ：仅对有约束的优化问题生效（无约束时配置了也不产生任何作用）。在等式或不等式中（约束条件），解理论值的计算值之间的差值小于ConstraintTolerance，就认为该值是可行解。

以上就完成了需要进行遗传算法的所有参数配置，对于其他选项可具体取Matlab帮助手册查看。

这里对算法停止条件说明一下

条件一：当算法迭代到MaxGenerations值，无论结果如何，都会停止，这种停止条件是我们要避免的。

条件二：当连续MaxStallGenerations代最佳适应度函数值的变化率的平均值（要计算这个平均值得运行MaxStallGenerations+1代）小于或等于 FunctionTolerance，则算法停止。

2.4 算法实现

Matlab 复制代码

% 补充变量上下界
lb = -10;  % 变量下界：x≥-10
ub = 10;   % 变量上界：x≤10
% 调用ga
[x, fval, exitflag, output, population,scores] = ga(fun, nVars, [], [], [], [], lb, ub, [], options);

rng是 MATLAB 函数使用默认算法和种子初始化 MATLAB 随机数生成器。

rng default是 MATLAB 中用于重置随机数生成器到默认初始状态的核心指令，其作用是让随机数生成结果可重复、可复现。确保每次运行代码时生成的随机数序列完全一致。可放在代码起始处。

对于函数求极值问题，自变量范围是必须的，否则很难找到答案。

'ga'函数的输入和输出参数比较多，对于不需要的输入参数用'[]'代替。这些参数的具体含义大家去查手册，这里解释一下输出参数

输出参数含义：

x：解，以实数向量形式返回。x是ga 在其迭代过程中找到的最佳点。也就是函数的最值点

fval: 解处的目标函数值，以实数形式返回，通常，fval = fun(x)，就是求取的最值

exitflag: ga停止的原因，以整数形式返回。成功返回1

output：有关优化过程的信息，以的结构体形式返回

Population：最终种群，以Population*nVars矩阵形式返回，内容就是一组x值

scores：最终得分，以列向量形式返回。就是对应的一组fun(x)的值

2.5 内容输出

Matlab 复制代码

disp('==================== 结果 ====================');
disp(['最优解 x = ', num2str(x)]);       
disp(['最优目标函数值 f(x) = ', num2str(fval)]);
disp(['终止原因 exitflag = ', num2str(exitflag)]);
disp(['实际迭代次数 = ', num2str(output.generations)]);

这个就是打印函数，没什么好解释

2.6 完整代码

Matlab 复制代码

clear; close;
rng default  %固定随机种子（保证结果可复现）

%创建匿名函数
function y = fitness(x)
    y = x + 10*sin(5*x)+7*cos(4*x);
end

% 创建函数句柄
fun = @(x) fitness(x);
nVars = 1; 
%原函数图像
figure
x1 = -10:0.01:10;
plot(x1,fitness(x1));
title('y = x + 10*sin(5*x) + 7*cos(4*x)');
grid on;%添加网格


% 算法参数设置
options = optimoptions('ga', ...
    'MaxGenerations', 100, ...                  % 增大最大迭代次数（默认100）
    'PopulationSize', 100, ...                  % 增大种群大小（默认20）
    'MaxStallGenerations', 20, ...               % 配置停滞代数限制（默认值为50）
    'Display', 'iter', ...                      % 显示迭代过程，观察收敛趋势
    'PlotFcn', @gaplotbestf, ...                % 绘制每代最优值曲线，直观判断收敛
    'SelectionFcn',@selectionroulette, ...      % 轮盘赌选择策略，默认策略
    'CrossoverFcn',@crossoverscattered,...      % 是用于没有线性约束问题的默认交叉函数
    'MutationFcn',@mutationadaptfeasible,...    % 非整数约束时的默认突变函数，自适应变异，无需设置概率
    'FunctionTolerance', 1e-4, ...              % 目标函数容差（默认1e-4）
    'ConstraintTolerance', 1e-6);               % 约束容差（无约束时不生效）

% 补充变量上下界
lb = -10;  % 变量下界：x≥-10
ub = 10;   % 变量上界：x≤10
% 调用ga
[x, fval, exitflag, output, population,scores] = ga(fun, nVars, [], [], [], [], lb, ub, [], options);  

% 输出结果
disp('==================== 结果 ====================');
disp(['最优解 x = ', num2str(x)]);       
disp(['最优目标函数值 f(x) = ', num2str(fval)]);
disp(['终止原因 exitflag = ', num2str(exitflag)]);
disp(['实际迭代次数 = ', num2str(output.generations)]);

三、结果分析

MATLAB 的ga函数默认最小化目标函数，目标函数（适应度函数）的输出值越小，对应的适应度权重越大，对应的个体被选择的概率越大。这是因为大多数工程 / 数学问题的优化需求是「最小化成本、误差、损耗」

因为前面配置中加入了**'Display', 'iter'，**所以会打印每次迭代的输出结果

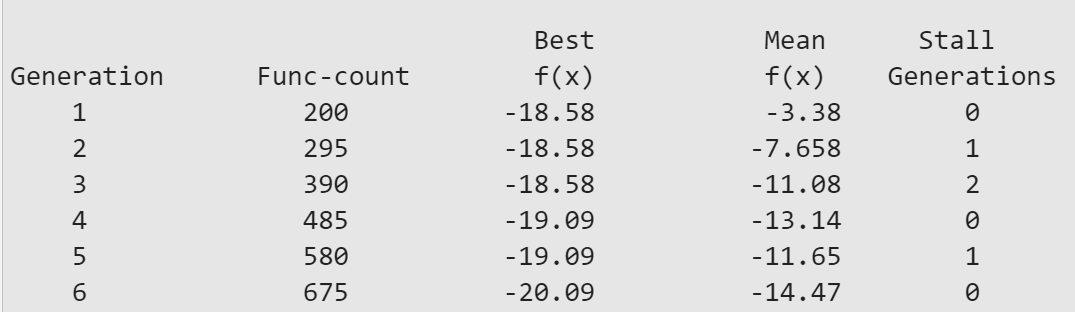
Generation：迭代代数，最多等于MaxGenerations

Func-count：调用适应度函数（fun(x)）的次数，代表从算法启动到当前迭代的累计总调用次数

Best f (x)：本次迭代的最优解，fun(x)的值

Mean f (x)：本次迭代的平均解，fun(x)的平均值

Stall Generations：表示最佳适应度函数值的已连续几代无变化

设置MaxStallGenerations = 50时看一下输出结果：

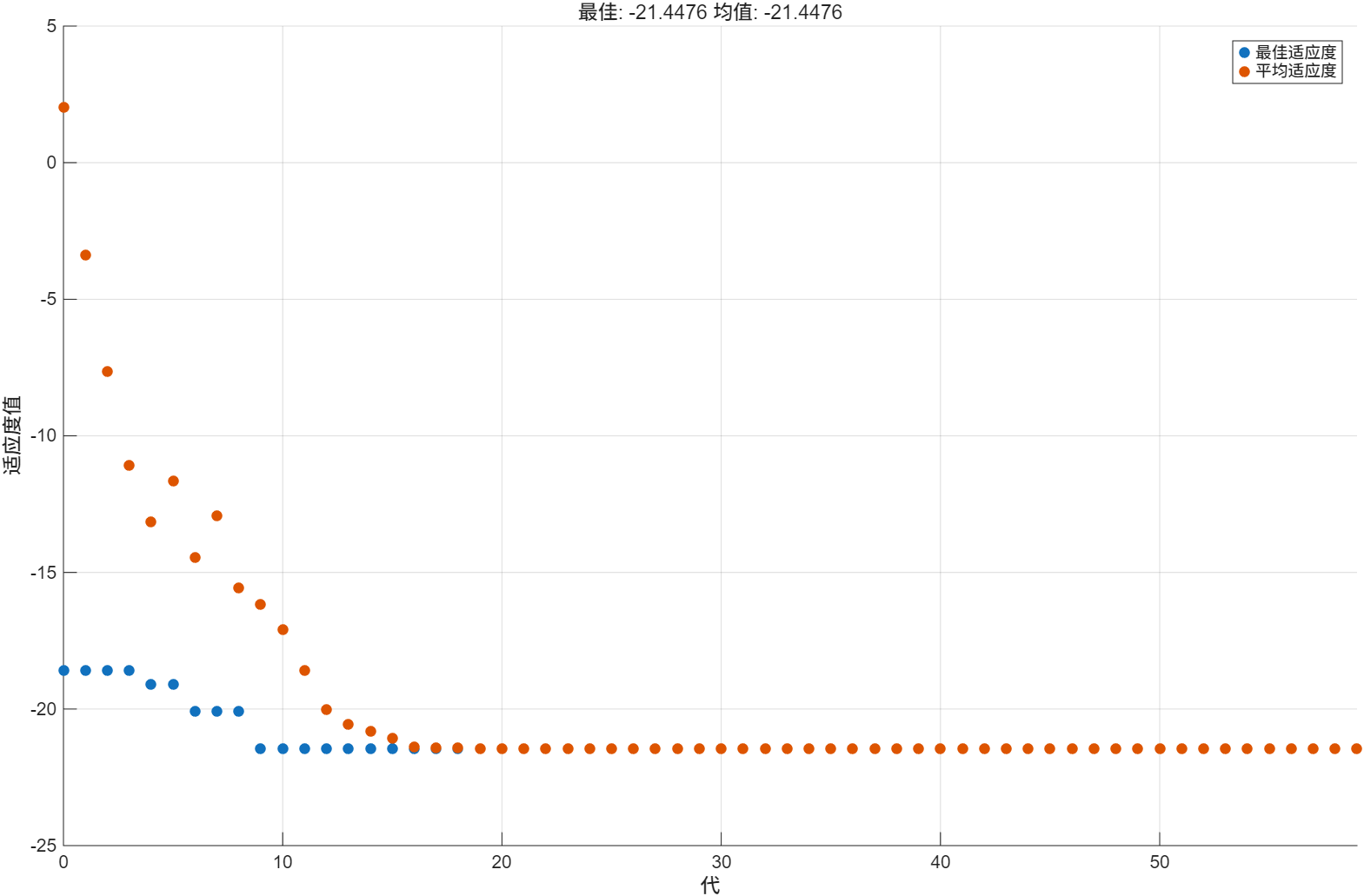
满足我们直观判断的5.3左右，从图中可以看出，只需要迭代到30代，就可以了。那么可以设置MaxStallGenerations = 20来减小计算时间

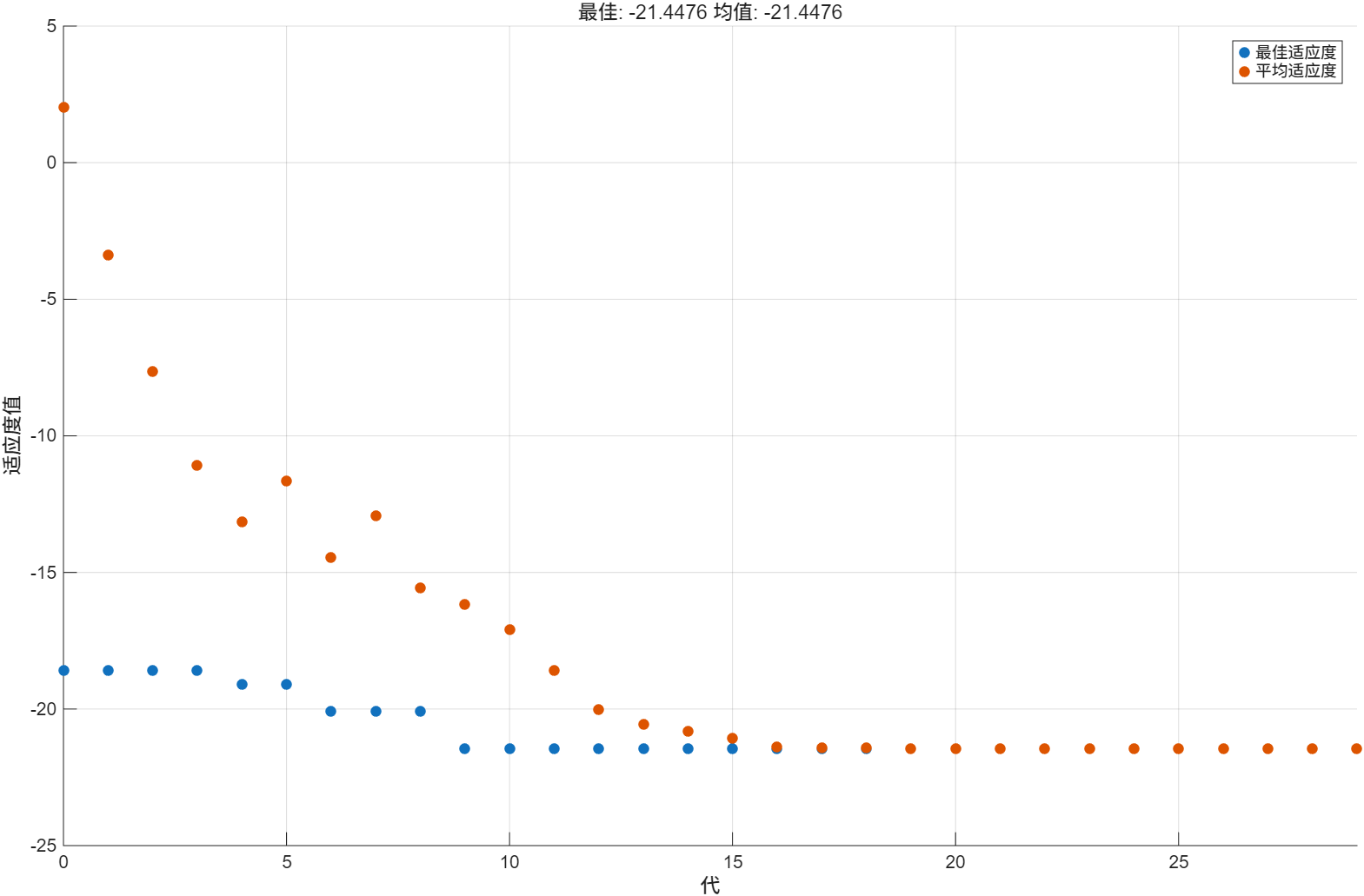
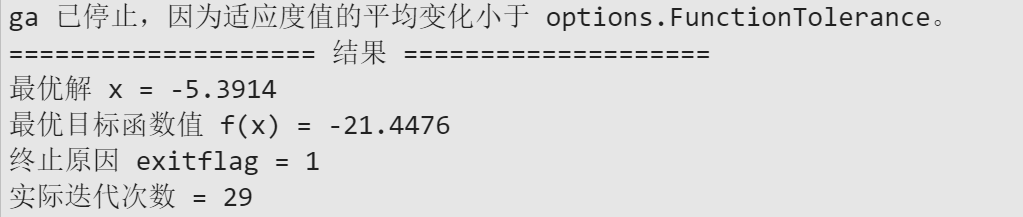
可以发现结果不变。

四、求最大值

4.1 取反操作

可以将函数句柄取反，这样原函数的输出值越大，适应度函数值越小，对应的适应度权重越大，从而最大值被迭代选出来，最后，把输出值取反恢复为原函数。

Matlab 复制代码

fun = @(x) -fitness(x);

Matlab 复制代码

[x, fval, exitflag, output, population,scores] = ga(fun, nVars, [], [], [], [], lb, ub, [], options);  
fval = -fval;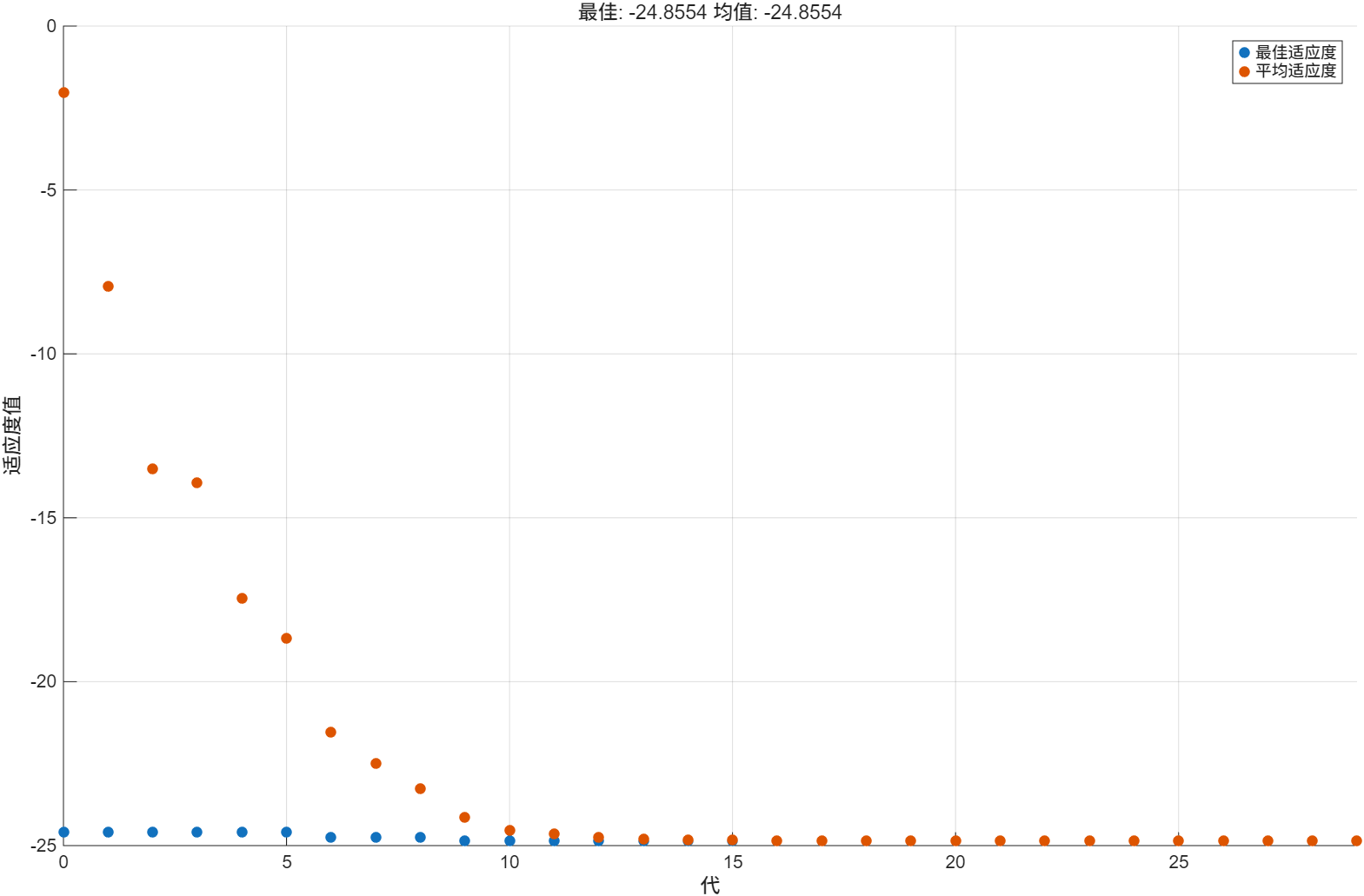

4.2 分式操作

Matlab 复制代码

function y = fitness(x)
    y = x + 10*sin(5*x)+7*cos(4*x);
    y = abs(1./(y+1e-4));
end

Matlab 复制代码

[x, fval, exitflag, output, population,scores] = ga(fun, nVars, [], [], [], [], lb, ub, [], options);  
fval = 1./fval - 1e-4;

直接对函数进行绝对值，取倒数操作。加入1e-4是防止分母为0。最后将输出fval变换成原函数值就行

只要明确原函数输出值和适应度权重的关系，多种操作都可

总结

我发现市面上好像不止一种ga函数，虽然输入参数和输出参数很像，但含义不同。我这使用的函数都是matlab官方工具箱内的，和官方函数说明文档对应。