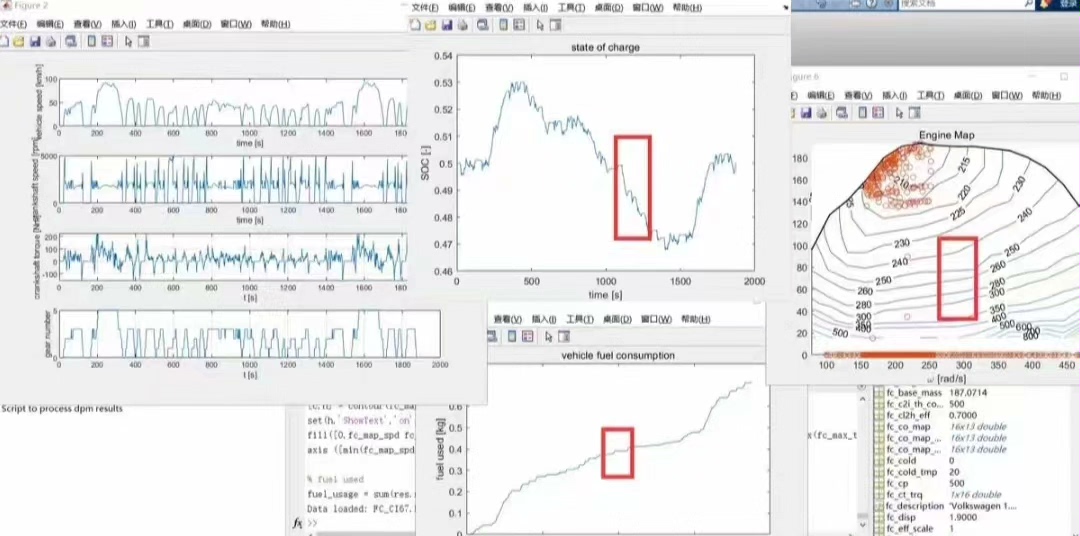
基于DP动态规划的混合动力汽车P2构型探索

基于DP动态规划的混合动力汽车，P2构型 1.车辆数据来源advisor。 2.电池SOC为电量维持型策略。 3.全程序包含逆向迭代和正向寻优过程。 4.DP可为后续mpc提供参考，也可将数据提取作为神经网络训练和规则作为参考。

最近在研究混合动力汽车这块，今天来跟大家唠唠基于DP动态规划的P2构型相关内容。

咱这次研究的车辆数据来源是advisor，它可是提供了不少关键信息，像车辆各部件的参数啥的，为后续的算法实现和分析奠定了基础。

先讲讲这个电量维持型策略，也就是电池SOC这块。在混合动力汽车运行过程中，电池电量的管理至关重要。采用电量维持型策略，就是要保证电池SOC在一个合理的范围内波动。比如说，设定一个SOC的上下限，假设下限是0.3，上限是0.8。代码实现上大概像这样：

python 复制代码

SOC = 0.5  # 初始SOC
lower_limit = 0.3
upper_limit = 0.8
if SOC < lower_limit:
    # 执行充电相关操作
    print("需要充电以维持电量")
elif SOC > upper_limit:
    # 执行放电相关操作
    print("可以适当放电")

这里简单模拟了根据SOC值判断车辆该执行何种操作，以此维持电池电量。

接下来讲讲整个程序流程，它包含逆向迭代和正向寻优过程。逆向迭代就像是从目的地往回找路。在混合动力汽车的语境里，我们从车辆行驶的终点状态开始，倒推每个时刻车辆应该采取的最优控制策略。比如说，我们已知车辆在最后时刻要达到某个速度、SOC状态等，然后逐步往前推算每个时间点发动机、电机该如何工作。

python 复制代码

# 假设这里有一个状态列表states，存储不同时刻的车辆状态
states = [1, 2, 3, 4, 5]  # 示例数据
for i in range(len(states) - 1, 0, -1):
    current_state = states[i]
    previous_state = states[i - 1]
    # 根据当前和前一个状态计算控制策略，这里简单示意
    control_strategy = current_state - previous_state
    print(f"从状态 {previous_state} 到 {current_state} 的控制策略: {control_strategy}")

这段代码简单模拟了逆向迭代过程，从后往前遍历状态列表并计算控制策略。

正向寻优则是从起点开始，根据当前的状态和各种约束条件，寻找最优的前行路径。结合混合动力汽车，就是在车辆启动时，基于当前的SOC、车速等初始条件，寻找在整个行驶过程中能使油耗最低、排放最优等目标的发动机和电机工作模式。

python 复制代码

# 正向寻优示例，假设一些初始条件
initial_SOC = 0.5
initial_speed = 0
# 遍历不同行驶阶段
for stage in range(10):
    # 根据当前阶段和初始条件计算新的状态和控制策略
    new_SOC = initial_SOC - 0.05 * stage
    new_speed = initial_speed + 5 * stage
    control_action = "发动机和电机协同工作" if new_SOC > 0.4 else "仅电机工作"
    print(f"阶段 {stage}: SOC {new_SOC}, 速度 {new_speed}, 控制动作 {control_action}")

这个正向寻优代码示例展示了在不同行驶阶段，根据初始条件调整车辆状态和控制动作。

最后说说DP动态规划的延伸应用。DP不仅能解决当下混合动力汽车P2构型的控制策略问题，还能为后续mpc（模型预测控制）提供参考。mpc可以基于DP得出的一些最优解和规律，进一步优化实时控制策略。另外，我们还可以把DP计算过程中提取的数据作为神经网络训练的样本，把得出的规则作为神经网络训练的参考。就好比给神经网络提供学习资料，让它更好地模拟和预测混合动力汽车的运行状态，实现更智能的控制。

总之，基于DP动态规划的混合动力汽车P2构型研究，从数据来源到电量策略，再到复杂的程序过程，以及未来的应用拓展，都充满了挑战与机遇，值得我们深入探索。