深度学习中 z-score 标准化
在深度学习中,z-score(标准分数) 是核心的数据预处理工具,用于将数据标准化为「均值 = 0、标准差 = 1」的分布,本质是衡量单个数据点相对于数据集整体的偏离程度。它不仅能提升模型训练效率(如加速收敛、避免梯度消失),还能消除特征量纲差异带来的影响(比如 "身高(cm)" 和 "体重(kg)" 无法直接比较的问题)。
一、核心定义与公式(通俗理解 + 数学表达)
1. 通俗类比
把数据集想象成一个班级的考试成绩:
-
均值(μ)= 班级平均分(比如 80 分)
-
标准差(σ)= 分数的 "波动范围"(比如 5 分,代表大多数人分数在 75-85 分之间)
*σ 是希腊字母 小写 sigma,发音为:
英文音标:/ˈsɪɡmə/
中文近似读音:"西格玛"(最常用且标准的中文音译)
-
z-score = 某个学生的分数相对于平均分的 "偏离等级":
-
若学生考 85 分,z-score=(85-80)/5=1 → 比平均分高 1 个标准差(处于中等偏上)
-
若学生考 70 分,z-score=(70-80)/5=-2 → 比平均分低 2 个标准差(处于下游)
-
2. 数学公式
对于单个数据点 x ,z-score 计算如下:
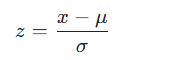
$
z = \frac{x - \mu}{\sigma}
$
-
\\mu :数据集的均值(mean)
-
\\sigma :数据集的标准差(standard deviation),且 \\sigma \> 0
-
结果含义:z-score 为正表示数据点大于均值,为负表示小于均值,绝对值越大偏离越远(通常 | z|>3 可视为异常值)
3. 批量数据标准化(深度学习常用)
对于深度学习中的特征矩阵(如形状为 [样本数,特征数] 的数据),标准化需按「特征维度」计算(即对每个特征单独算 μ 和 σ):
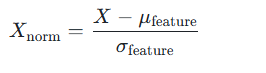

$
X_{\text{norm}} = \frac{X - \mu_{\text{feature}}}{\sigma_{\text{feature}}}
$
-
\\mu_{\\text{feature}} :每个特征维度的均值(而非所有数据的全局均值)
-
\\sigma_{\\text{feature}} :每个特征维度的标准差
-
例:若数据是图像(形状 [N, H, W, C],N = 样本数,C = 通道数),则按「通道维度」计算 μ 和 σ(比如 RGB 图像的 R、G、B 通道分别标准化)
二、具体计算步骤(带示例)
假设深度学习任务中,某特征(如 "图像像素亮度")的数据集为:[10, 20, 30, 40, 50],按步骤计算 z-score:
| 步骤 | 计算过程 | 结果 |
|---|---|---|
| 1. 计算均值 μ | (10+20+30+40+50)/5 = 30 | μ=30 |
| 2. 计算标准差 σ | 先算方差:[(10-30)²+(20-30)²+(30-30)²+(40-30)²+(50-30)²]/5 = 200标准差 =√200 ≈14.14 | σ≈14.14 |
| 3. 逐个计算 z-score | 10→(10-30)/14.14≈-1.4120→(20-30)/14.14≈-0.7130→040→0.7150→1.41 | 标准化后数据:[-1.41, -0.71, 0, 0.71, 1.41] |
最终标准化后的数据:均值≈0,标准差≈1,且消除了原始数据的量纲(比如原始数据单位是 "亮度值",标准化后无单位)。
三、深度学习中的核心应用场景(结合实际任务)
z-score 标准化是深度学习预处理的 "标配操作",尤其适用于以下场景:
| 应用场景 | 具体说明 | 案例(如 YOLO、神经网络) |
|---|---|---|
| 1. 加速模型收敛 | 很多激活函数(如 sigmoid、tanh)在输入值过大 / 过小时梯度趋近于 0(梯度消失),标准化后输入集中在 [-3,3],梯度更稳定 | 训练 YOLO 目标检测模型时,对图像像素值(0-255)标准化为 z-score,避免卷积层梯度消失 |
| 2. 消除特征量纲差异 | 多特征输入时(如 "图像尺寸(像素)""物体面积(cm²)"),量纲不同会导致模型偏向权重更大的特征,标准化后所有特征权重平等 | 基于深度学习的推荐系统中,对 "用户点击次数(次)" 和 "用户停留时间(秒)" 标准化,避免模型过度关注 "次数" 特征 |
| 3. 异常值检测 | 标准化后 | z |
| 4. 提升模型泛化能力 | 标准化让数据分布更稳定,减少训练集与测试集的分布差异(domain gap) | 迁移学习中,对新数据集按预训练模型的 μ 和 σ 标准化(而非新数据集自身),提升模型迁移效果 |
四、z-score vs 其他标准化方法(表格对比)
深度学习中常用的标准化方法还有 Min-Max 缩放(归一化),两者适用场景不同,对比如下:
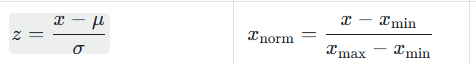
| 对比维度 | z-score 标准化 | Min-Max 缩放(归一化) | 适用场景 |
|---|---|---|---|
| 公式 | z = \\frac{x-\\mu}{\\sigma} | x_{\\text{norm}} = \\frac{x - x_{\\text{min}}}{x_{\\text{max}} - x_{\\text{min}}} | - |
| 输出范围 | 无固定范围(通常 [-3,3]) | [0,1](或 [-1,1]) | 需固定输入范围时(如 CNN 输入层、GAN 生成器)用 Min-Max |
| 对异常值敏感 | 较低(依赖均值和标准差,异常值影响小) | 较高(依赖最大值 / 最小值,异常值会严重扭曲结果) | 数据含较多异常值时用 z-score |
| 数据分布假设 | 无需假设分布(但正态分布下效果最优) | 无分布假设 | 数据非正态分布但需固定范围时用 Min-Max |
| 深度学习优先级 | 更高(大多数神经网络、CNN、Transformer 首选) | 较低(仅特定场景用) | 训练 YOLO、ResNet、BERT 等模型时优先 z-score |
关键结论:如果没有特殊要求(如输入必须在 [0,1]),深度学习任务优先使用 z-score 标准化,尤其是基于梯度下降的模型(如神经网络、深度学习分类器)。
五、常见问题与注意事项(避坑指南)
-
标准化的 "数据泄露" 问题:
必须用训练集的 μ 和 σ标准化测试集 / 验证集,而非整个数据集(包括测试集)的 μ 和 σ,否则会泄露测试集信息,导致泛化能力下降。
例:用 PyTorch 的
torchvision.transforms.Normalize(mean, std)时,mean 和 std 需来自 ImageNet 等训练集,而非自己的测试集。 -
标准差为 0 的处理:
若某特征所有数据相同(σ=0),标准化会除以 0,此时需删除该特征(无区分度)或替换为 0。
-
非正态分布数据是否能用?
可以!z-score 不要求数据必须是正态分布,只是正态分布下标准化后的数据更易解释(如 68% 的数据在 [-1,1],95% 在 [-2,2]),非正态分布下仍能消除量纲差异。
-
批量标准化(BatchNorm)与 z-score 的关系:
BatchNorm 是深度学习中的 "动态标准化",本质是在训练过程中对每个 batch 的输入按 z-score 标准化(再通过 γ 和 β 参数调整分布),解决了 z-score "静态标准化"(仅用训练集 μ 和 σ)的局限性,是 z-score 的进阶应用。
六、代码实现(Python / 深度学习框架)
1. 基础 Python 实现(手动计算)
import numpy as np
\# 模拟深度学习中的特征数据(形状:\[样本数, 特征数])
data = np.array(\[\[10, 20], \[20, 30], \[30, 40], \[40, 50], \[50, 60]])
\# 按特征维度计算μ和σ(axis=0表示按列计算)
mu = np.mean(data, axis=0) # 每个特征的均值:\[30, 40]
sigma = np.std(data, axis=0) # 每个特征的标准差:\[\~14.14, \~14.14]
\# z-score标准化
z\_score\_data = (data - mu) / sigma
print("标准化后数据:\n", z\_score\_data)
print("标准化后均值:", np.mean(z\_score\_data, axis=0)) # 接近\[0, 0]
print("标准化后标准差:", np.std(z\_score\_data, axis=0)) # 接近\[1, 1]2. PyTorch/TensorFlow 实现(深度学习实战)
\# PyTorch示例(YOLO图像预处理)
import torch
from torchvision import transforms
\# 按ImageNet的均值和标准差标准化(深度学习常用预训练参数)
transform = transforms.Compose(\[
  transforms.ToTensor(), # 转换为\[0,1]张量
  transforms.Normalize(mean=\[0.485, 0.456, 0.406], # ImageNet的RGB通道均值
  std=\[0.229, 0.224, 0.225]) # ImageNet的RGB通道标准差
])
\# TensorFlow示例
import tensorflow as tf
\# 模拟图像数据(\[样本数, 高度, 宽度, 通道数])
images = tf.random.uniform(\[32, 224, 224, 3]) # 32张224x224的RGB图像
mu = tf.reduce\_mean(images, axis=\[0,1,2]) # 按通道计算均值(axis=\[样本, 高度, 宽度])
sigma = tf.math.reduce\_std(images, axis=\[0,1,2])
images\_zscore = (images - mu) / sigma总结
z-score 是深度学习中 "最简单且最有效的预处理工具",核心作用是统一数据分布、消除量纲差异、稳定模型训练。记住三个关键要点:
-
公式:z=(x-μ)/σ,按特征维度计算;
-
应用:优先用于神经网络、CNN、YOLO 等模型,避免梯度消失和量纲干扰;
-
避坑:用训练集 μ/σ 标准化测试集,避免数据泄露。
如果在具体任务(如 YOLO 训练、Transformer 特征处理)中遇到标准化相关问题,可以进一步探讨!
(注:文档部分内容可能由 AI 生成)