Comsol 下光子晶体仿真：从拓扑荷到偏振态的奇妙之旅

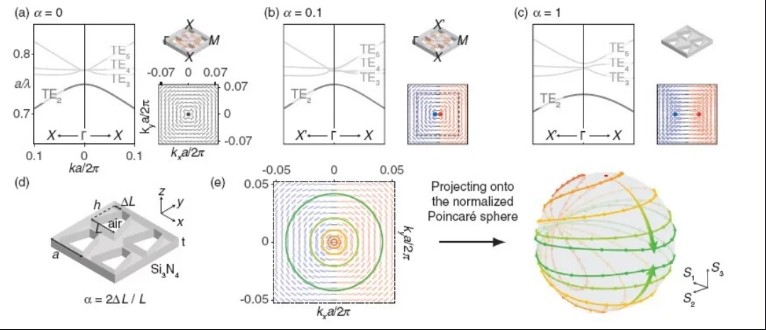
comsol光子晶体仿真，拓扑荷，偏振态。三维能带，三维Q，Q因子计算。远场偏振计算。

在光子晶体领域的研究中，Comsol 是一款强大的仿真工具，它能帮助我们深入探究光子晶体的各种特性。今天咱们就来聊聊基于 Comsol 的光子晶体仿真里，拓扑荷、偏振态以及与之紧密相关的三维能带、三维 Q 因子计算和远场偏振计算这些有趣的话题。

三维能带仿真

三维能带描述了光子在光子晶体中的能量分布情况，对理解光子晶体的光学性质至关重要。在 Comsol 中，我们可以通过以下步骤来实现三维能带的仿真。

首先，建立光子晶体的三维几何模型。假设我们构建一个简单的立方晶格结构的光子晶体，以下是部分可能用到的脚本（这里以类似 Python 的伪代码示意，实际 Comsol 有其特定脚本语言）：

python 复制代码

# 创建三维几何对象
geometry = model.geom.create('geom1', 3)
# 添加立方体作为基本结构单元
cube = geometry.feature.create('cube1', 'Block')
cube.set('size', [a, a, a])  # a 为晶格常数

接着，定义材料属性，为光子晶体和背景赋予合适的介电常数：

python 复制代码

mat1 = model.materials.create('mat1')
mat1.select(geometry.region(1))
mat1.property.set('epsr', epsilon1)  # epsilon1 为光子晶体材料介电常数

mat2 = model.materials.create('mat2')
mat2.select(geometry.region(2))
mat2.property.set('epsr', epsilon2)  # epsilon2 为背景材料介电常数

然后，设置电磁波的激励条件以及边界条件：

python 复制代码

emw = model.physics.create('emw', 'Electromagnetic Waves, Frequency Domain')
emw.boundary('bnd1').set('condition', 'Electric Wall')  # 设置边界为电壁条件
emw.source('src1').set('E0', [1, 0, 0])  # 设置电场激励方向

通过以上步骤，再利用 Comsol 内置的求解器进行计算，我们就能得到光子晶体的三维能带结构。这个能带结构展示了光子能量与波矢的关系，不同的能带区域代表了光子在晶体中允许或禁止传播的能量范围。

三维 Q 因子计算

三维 Q 因子是衡量光子晶体微腔品质的重要参数。Q 因子越高，意味着微腔中光子的寿命越长，能量损耗越小。在 Comsol 里计算三维 Q 因子，关键在于准确找到微腔模式并分析其损耗特性。

以一个简单的点缺陷型光子晶体微腔为例，我们在上述模型基础上，通过修改局部晶格结构来引入点缺陷形成微腔：

python 复制代码

# 修改点缺陷位置的晶格结构
defect = geometry.feature.create('defect1', 'Cylinder')
defect.set('radius', r_defect)
defect.set('height', a)
defect.set('position', [x_defect, y_defect, z_defect])

在求解时，关注微腔模式的共振频率以及能量损耗。这里涉及到一些对场分布和能量计算的操作，以下是简化后的示意：

python 复制代码

# 获取微腔模式的电场分布
E_field = emw.solution('sol1').field('E')
# 计算微腔中的储存能量
U = emw.evaluate('intop1(0.5*eps0*epsr*abs(E_field)^2)')
# 计算能量损耗率
P_loss = emw.evaluate('intop1(0.5*real(sigma*abs(E_field)^2))')
# 计算 Q 因子
Q_factor = 2 * pi * f_resonance * U / P_loss

这里 f_resonance 是微腔的共振频率，通过这样的计算，我们就得到了三维 Q 因子，它对于评估光子晶体微腔在光学滤波、激光等应用中的性能具有重要意义。

拓扑荷与偏振态

拓扑荷是光子晶体中一个独特的物理量，它与光子晶体的能带拓扑性质相关联。而偏振态则描述了光矢量的振动方向。二者之间存在着微妙的联系。

在 Comsol 仿真中，我们可以通过设置不同的激励源偏振方向来研究拓扑荷对偏振态的影响。例如，设置线偏振激励：

python 复制代码

emw.source('src1').set('E0', [1, 0, 0])  # 沿 x 方向线偏振

当光子晶体具有特定的拓扑荷时，在传播过程中，光的偏振态可能会发生有趣的变化。这种变化可以通过观察远场的偏振分布来研究。

远场偏振计算

远场偏振计算能让我们了解光在远离光子晶体后的偏振特性。在 Comsol 中，我们利用远场计算模块来实现这一目的。

首先，在求解完成后，激活远场计算：

python 复制代码

farfield = model.results.create('farfield1', 'Far - Field Calculation')
farfield.set('coordinate_system', 'Spherical')
farfield.set('reference_point', [0, 0, 0])

然后，通过后处理操作获取远场的电场分量，进而计算偏振态相关参数，比如偏振度：

python 复制代码

# 获取远场电场分量
Etheta = farfield.evaluate('Etheta')
Ephi = farfield.evaluate('Ephi')
# 计算偏振度
DoP = (abs(Etheta)^2 - abs(Ephi)^2) / (abs(Etheta)^2 + abs(Ephi)^2)

通过这样的计算，我们能清晰地看到远场不同方向上的偏振状态，这对于设计基于光子晶体的偏振相关光学器件有着重要的指导作用。

通过 Comsol 的强大功能，我们在光子晶体的仿真研究中，深入挖掘了拓扑荷、偏振态、三维能带以及三维 Q 因子等关键特性，为光子晶体在光学领域的进一步应用和创新奠定了基础。希望这篇文章能为对光子晶体仿真感兴趣的小伙伴们带来一些启发。