目录
[1. 189. 轮转数组](#1. 189. 轮转数组)
[2. 55. 跳跃游戏](#2. 55. 跳跃游戏)
[3. 238. 除自身以外数组的乘积](#3. 238. 除自身以外数组的乘积)
[4. 142. 环形链表 II](#4. 142. 环形链表 II)
[5. 28. 找出字符串中第一个匹配项的下标](#5. 28. 找出字符串中第一个匹配项的下标)
最近刷了几道 LeetCode 经典中等题,都是面试高频考点,整理了解法 + 核心思路,分享给大家~
1. 189. 轮转数组
题目 :将数组元素向右轮转 k 个位置(k 非负)。示例 :输入[1,2,3,4,5,6,7],k=3 → 输出[5,6,7,1,2,3,4]
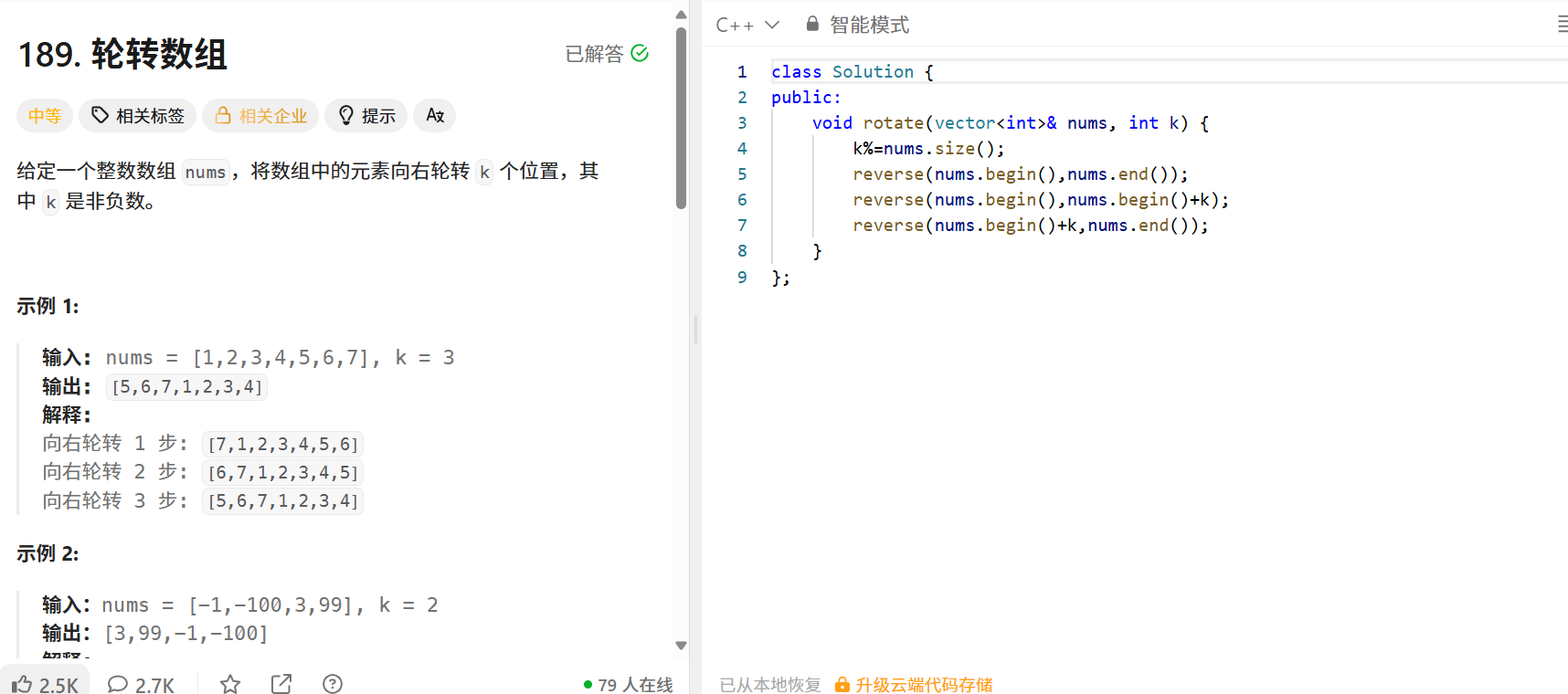
解法(三次反转法):
cpp
class Solution {
public:
void rotate(vector<int>& nums, int k) {
k %= nums.size(); // 避免k超过数组长度
reverse(nums.begin(), nums.end()); // 反转整个数组
reverse(nums.begin(), nums.begin()+k); // 反转前k个元素
reverse(nums.begin()+k, nums.end()); // 反转剩余元素
}
};核心思路 :通过三次反转实现 "轮转",时间复杂度 O (n),空间复杂度 O (1)(原地操作)。比如[1,2,3,4,5,6,7] → 全反转[7,6,5,4,3,2,1] → 反转前 3 个[5,6,7,4,3,2,1] → 反转后 4 个[5,6,7,1,2,3,4]。
2. 55. 跳跃游戏
题目 :初始在数组第一个下标,每个元素是最大跳跃长度,判断能否到达最后一个下标。示例 :输入[2,3,1,1,4] → 输出true
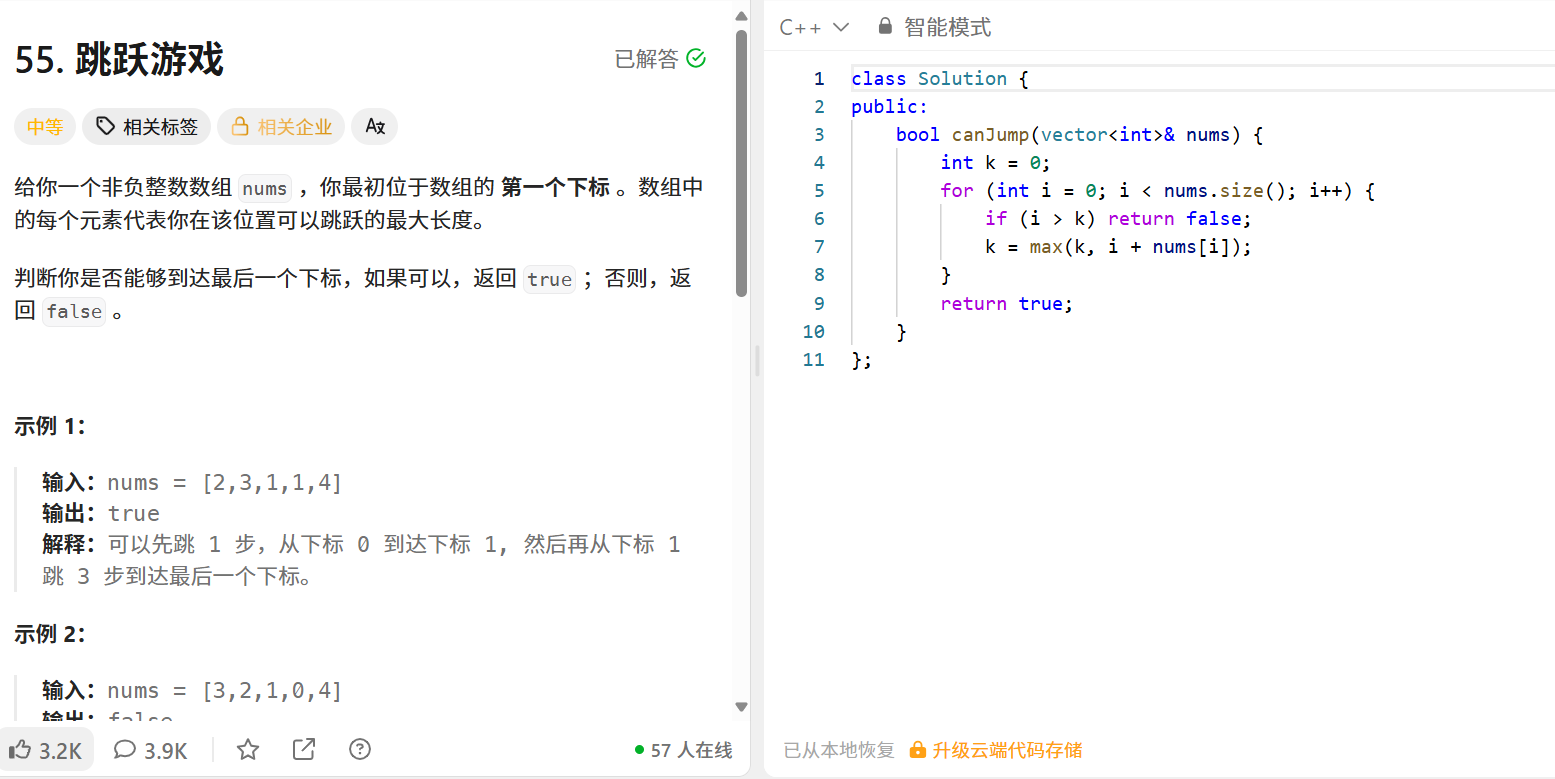
解法(贪心算法):
cpp
class Solution {
public:
bool canJump(vector<int>& nums) {
int max_reach = 0; // 记录当前能到达的最远位置
for (int i = 0; i < nums.size(); i++) {
if (i > max_reach) return false; // 无法到达当前位置
max_reach = max(max_reach, i + nums[i]);
}
return true;
}
};核心思路:不用纠结每一步跳多远,只维护 "当前能到达的最远位置"。如果遍历到某位置时,该位置超过了最远位置 → 无法到达终点;否则更新最远位置,最终判断是否能覆盖终点。
3. 238. 除自身以外数组的乘积
题目 :返回数组answer,其中answer[i]是数组中除nums[i]外所有元素的乘积(不能用除法,时间 O (n))。示例 :输入[1,2,3,4] → 输出[24,12,8,6]
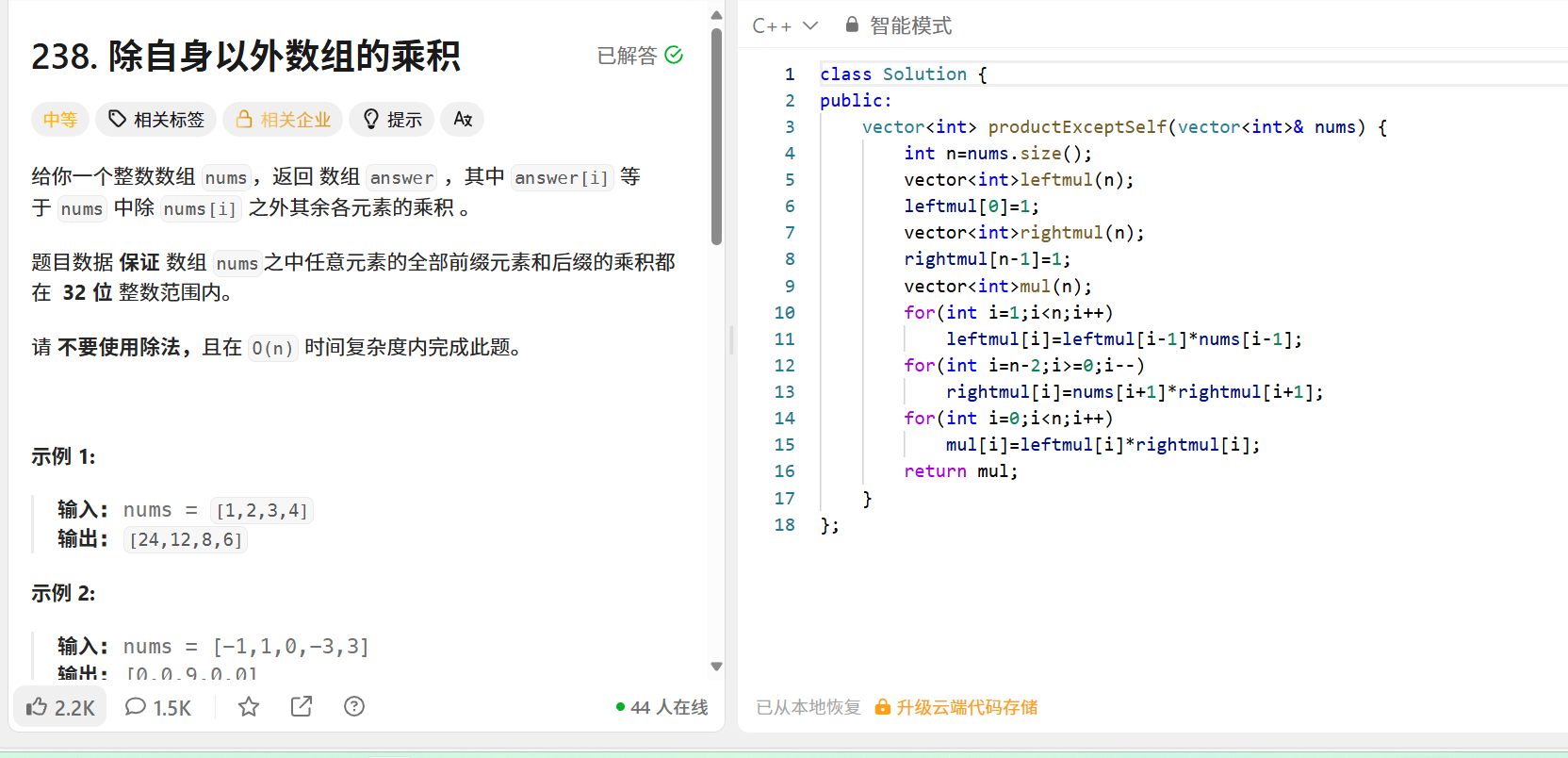
解法(左右前缀积):
cpp
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> left(n, 1); // left[i]:nums[0..i-1]的乘积
vector<int> right(n, 1); // right[i]:nums[i+1..n-1]的乘积
for (int i = 1; i < n; i++) left[i] = left[i-1] * nums[i-1];
for (int i = n-2; i >= 0; i--) right[i] = right[i+1] * nums[i+1];
vector<int> res(n);
for (int i = 0; i < n; i++) res[i] = left[i] * right[i];
return res;
}
};核心思路 :用两个数组分别存 "前缀积" 和 "后缀积",最终answer[i] = 前缀积[i] * 后缀积[i]。空间复杂度 O (n),也可以优化到 O (1)(用结果数组存前缀积,再逆序乘后缀积)。
4. 142. 环形链表 II
题目 :找到链表入环的第一个节点,无环则返回 null。示例 :链表3→2→0→-4→2 → 入环点是 2。
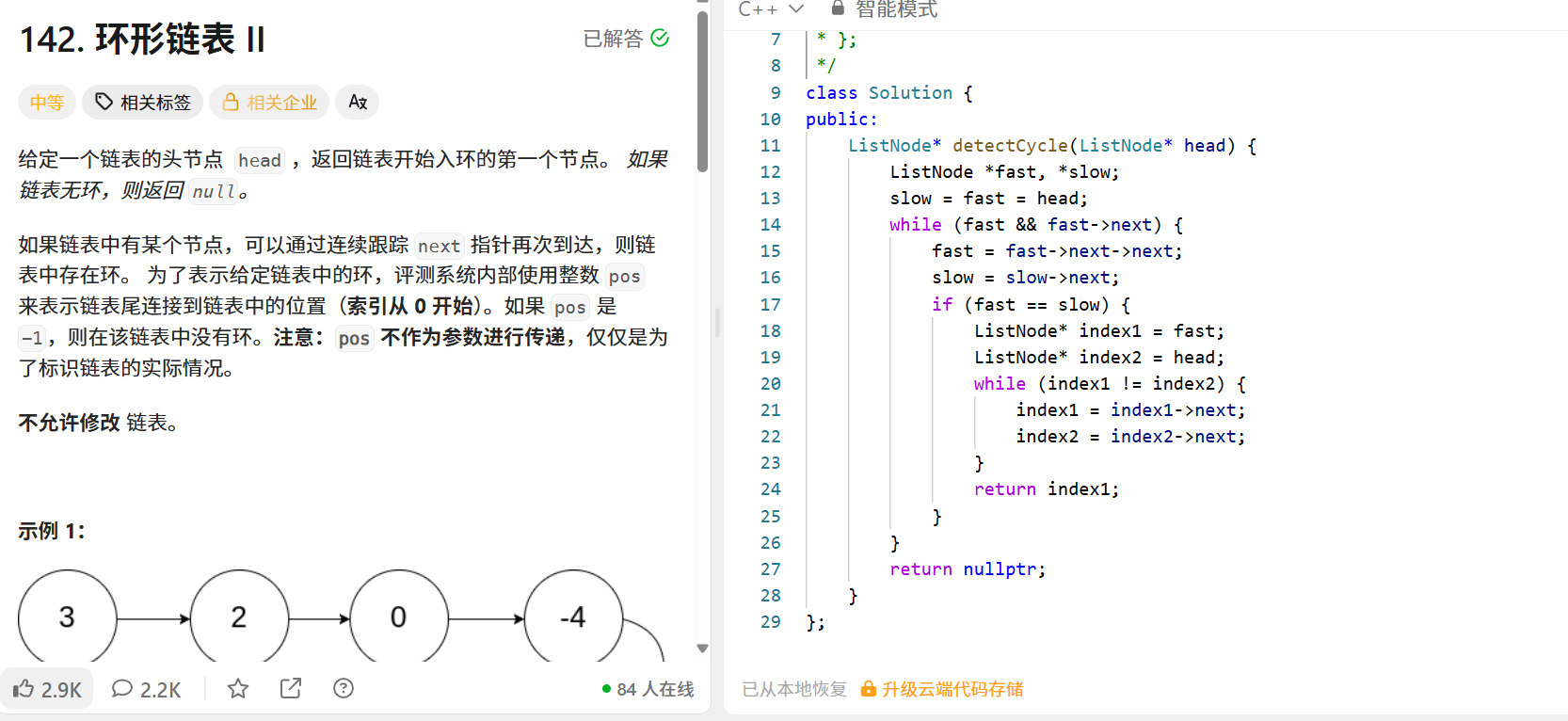
解法(快慢指针):
cpp
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *slow = head, *fast = head;
// 第一步:快慢指针找相遇点
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
// 第二步:相遇点和头节点同时出发,相遇点即入环点
ListNode *p1 = head, *p2 = slow;
while (p1 != p2) {
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
}
return nullptr;
}
};核心思路:
- 快慢指针(快 2 步、慢 1 步),若有环则必相遇;
- 相遇后,一个指针从表头出发,另一个从相遇点出发,同速前进 ,相遇点就是入环点(数学推导:设表头到入环点距离 a,入环点到相遇点距离 b,环长 c,则
2(a+b) = a + b + kc→a = (k-1)c + (c-b))。
5. 28. 找出字符串中第一个匹配项的下标
题目 :在 haystack 中找 needle 的第一个匹配下标,无则返回 - 1。示例 :输入haystack="sadbutsad", needle="sad" → 输出 0
解法(直接调用库函数,面试需手写 KMP):
cpp
class Solution {
public:
int strStr(string haystack, string needle) {
return haystack.find(needle); // 库函数实现,面试建议手写KMP
}
};补充:KMP 算法(避免暴力匹配的重复比较) :核心是预处理 needle 得到前缀函数数组(记录每个位置的最长相等前后缀长度),然后用前缀函数快速匹配,时间复杂度 O (n+m)。
以上就是 5 道题的解法和思路啦~这些题都是面试常考的 "中等难度",掌握思路后能举一反三~
| 题目编号及名称 | 核心解法 | 核心思路 | 注意事项 & 思路亮点 |
|---|---|---|---|
| 189. 轮转数组 | 三次反转法 | 1. 先对k取模(k≥数组长度时简化操作);2. 反转整个数组;3. 反转前k个元素;4. 反转剩余元素。通过反转操作的组合,实现元素的轮转效果。 | • 亮点:原地操作,时间复杂度O(n),空间复杂度O(1),避免额外数组开销;• 注意:k可能大于数组长度,必须先执行k %= nums.size(),否则会出现越界或无效操作。 |
| 55. 跳跃游戏 | 贪心算法 | 1. 维护"当前能到达的最远位置"max_reach;2. 遍历数组,若当前索引超过max_reach,说明无法到达该位置,直接返回false;3. 否则更新max_reach为当前索引+当前元素值的最大值;4. 遍历结束后,若max_reach≥数组末尾索引,返回true。 | • 亮点:无需模拟跳跃过程,仅通过贪心策略维护最远可达位置,时间复杂度O(n),高效简洁;• 注意:初始max_reach为0,遍历从索引0开始,覆盖所有可能的跳跃起点。 |
| 238. 除自身以外数组的乘积 | 左右前缀积法 | 1. 定义left数组:left[i]表示nums[0..i-1]的乘积;2. 定义right数组:right[i]表示nums[i+1..n-1]的乘积;3. 遍历计算left和right数组;4. 结果数组res[i] = left[i] * right[i]。 | • 亮点:规避除法(避免除数为0问题),时间复杂度O(n);• 优化点:可将空间复杂度降至O(1),用res数组先存left值,再逆序遍历乘right值(无需额外right数组)。 |
| 142. 环形链表 II | 快慢指针法 | 1. 快慢指针初始化指向表头,快指针每次走2步,慢指针每次走1步;2. 若有环,两指针必相遇;3. 相遇后,一个指针从表头出发,另一个从相遇点出发,两指针同速前进,相遇点即为入环点;4. 若无环,快指针会先到达null。 | • 亮点:通过数学推导确定入环点,无需额外空间(空间复杂度O(1)),避免哈希表存储节点的开销;• 数学依据:设表头到入环点距离为a,入环点到相遇点距离为b,环长为c,则2(a+b) = a+b+kc → a=(k-1)c+(c-b)。 |
| 28. 找出字符串中第一个匹配项的下标 | KMP算法(面试推荐)/ 库函数 | KMP核心:1. 预处理模式串needle,生成前缀函数数组(记录每个位置的最长相等前后缀长度);2. 用双指针分别遍历主串haystack和模式串needle,利用前缀函数快速跳过重复比较,匹配成功则返回起始索引。 | • 亮点:KMP算法时间复杂度O(n+m)(n为主串长度,m为模式串长度),避免暴力匹配的O(nm)复杂度;• 注意:库函数haystack.find(needle)可快速解题,但面试中需手写KMP算法,核心是前缀函数的理解与实现。 |