Matlab/Simulink 半车主动悬架建模：ADRC 与 PID 的碰撞之旅

matlab/simulink半车主动悬架建模：基于ADRC(自抗扰控制)的主动悬架控制。主体模型为半车主动悬架，采取ADRC控制。输出为车身加速度，悬架动挠度，轮胎动变形。默认输入为正弦路面输入。有与pid控制的效果对比。

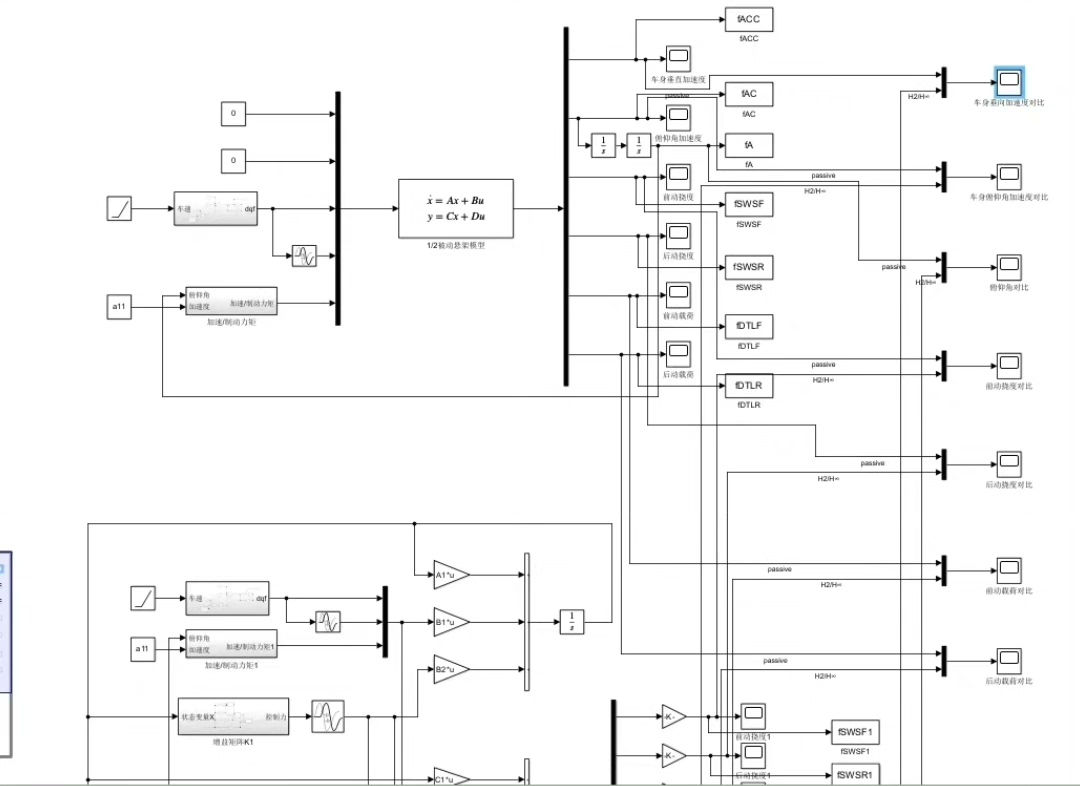
在汽车悬架系统的研究领域，如何提升车辆行驶的平顺性和操纵稳定性一直是热门话题。今天咱就来唠唠基于 Matlab/Simulink 的半车主动悬架建模，主角是自抗扰控制（ADRC），顺便和经典的 PID 控制来个效果大比拼。

半车主动悬架主体模型搭建

咱先把半车主动悬架模型在 Simulink 里搞起来。这个模型就像是汽车悬架的一个简化"替身"，它主要考虑车身垂直方向的运动、悬架的压缩与拉伸，以及轮胎与路面的接触变形。在 Simulink 里，我们可以通过各种模块来构建这个模型，就像搭乐高一样。

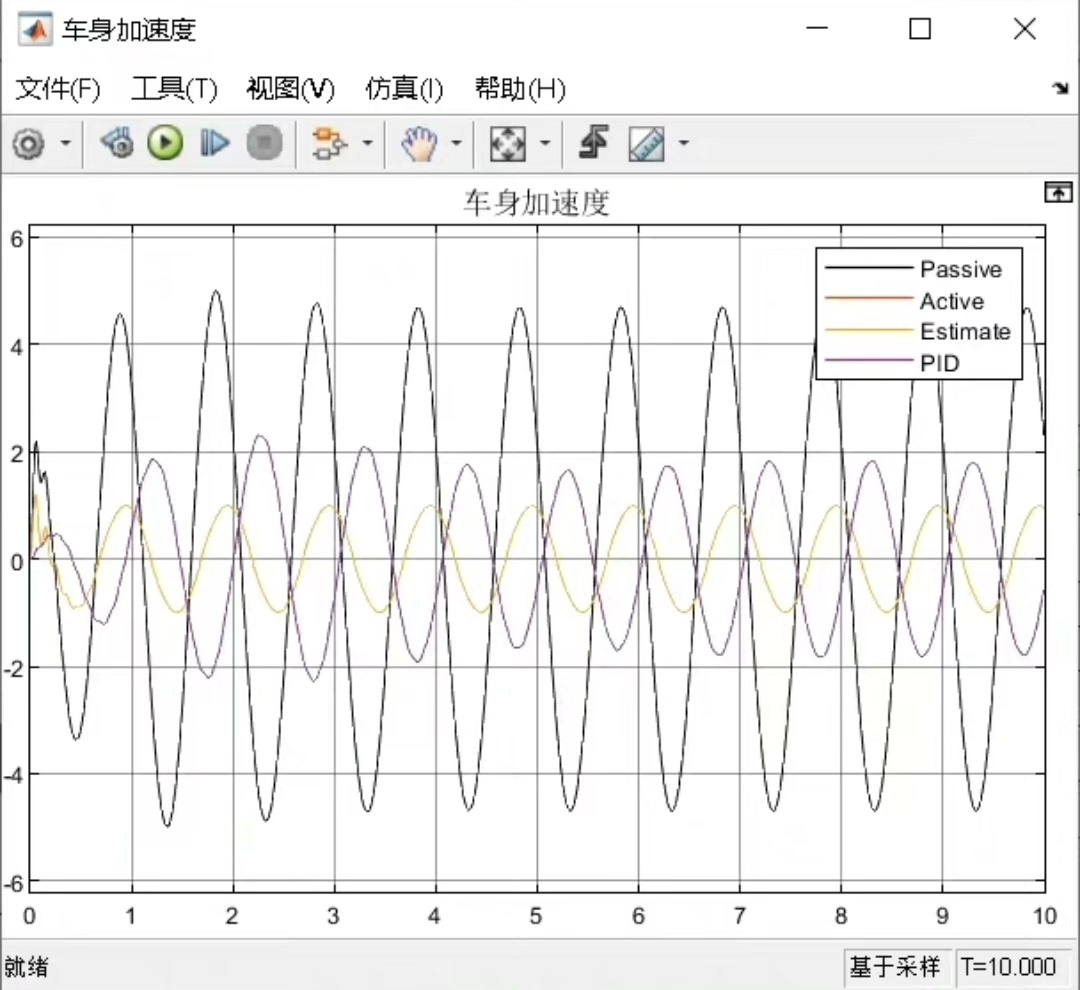
比如，车身质量可以用一个积分器模块来模拟其运动，悬架弹簧和阻尼则可以用相应的力模块来表示。这里简单给个伪代码示意一下悬架力的计算（Matlab 风格）：

matlab 复制代码

% 假设已经定义了弹簧刚度 k 和阻尼系数 c
% 悬架动挠度 z_s - z_u
deflection = z_s - z_u; 
% 悬架力 F_suspension = k * deflection + c * (dz_s/dt - dz_u/dt)
F_suspension = k * deflection + c * (diff(z_s)/dt - diff(z_u)/dt);

这里 zs**是车身位移，z u 是悬架下质量位移，通过这些计算来模拟悬架力对车身运动的影响。

ADRC 控制闪亮登场

ADRC 这玩意儿可不简单，它能把系统内部和外部的干扰统统"抗住"，让系统输出更稳定。在 Simulink 里实现 ADRC 控制，首先得了解它的几个关键部分：跟踪微分器（TD）、扩张状态观测器（ESO）和非线性状态误差反馈控制律（NLSEF）。

跟踪微分器（TD）

TD 的作用是安排过渡过程，让系统输出能够平滑地跟踪输入信号。咱来段简单的 TD 代码：

matlab 复制代码

function [x1, x2] = TD(r, h, x1, x2)
    % r 是输入参考信号，h 是步长
    d = r * h;
    a0 = x2;
    y = x1 - r;
    a1 = sqrt(a0^2 + 8 * r * abs(y) / h);
    if a0 >= 0
        a = (a0 + a1) / 2;
    else
        a = (a0 - a1) / 2;
    end
    if abs(y) <= d
        x2 = x2 - (a / h) * y;
    else
        x2 = x2 - sign(y) * r;
    end
    x1 = x1 + h * x2;
end

这段代码通过不断调整 x1 和 x2，让 x1 能够较好地跟踪输入 r，并且输出是平滑的，避免了传统直接跟踪可能出现的超调等问题。

扩张状态观测器（ESO）

ESO 就像是一个"侦察兵"，能实时观测系统的状态和干扰。代码大概长这样：

matlab 复制代码

function [z1, z2, z3] = ESO(y, u, z1, z2, z3, b0, beta01, beta02, beta03, alpha1, alpha2, alpha3, h)
    % y 是系统输出，u 是控制输入
    e = z1 - y;
    z1 = z1 + h * (z2 - beta01 * fal(e, alpha1, delta));
    z2 = z2 + h * (z3 - beta02 * fal(e, alpha2, delta) + b0 * u);
    z3 = z3 - h * beta03 * fal(e, alpha3, delta);
end

这里通过不断更新 z1、z2 和 z3，把系统状态和干扰都给"观测"出来了，为后续的控制提供有力支持。

非线性状态误差反馈控制律（NLSEF）

有了 TD 和 ESO 的成果，NLSEF 就负责根据观测到的状态和误差来计算最终的控制输入。代码类似这样：

matlab 复制代码

function u0 = NLSEF(v1, v2, z1, z2, z3, kp, kd, alpha01, alpha02, delta)
    e1 = v1 - z1;
    e2 = v2 - z2;
    u0 = kp * fal(e1, alpha01, delta) + kd * fal(e2, alpha02, delta) - z3;
end

通过这几个部分的协同工作，ADRC 就能实现对主动悬架的有效控制啦。

PID 控制也来凑个热闹

PID 控制作为控制领域的"老大哥"，简单易懂还好用。在 Simulink 里，PID 控制模块直接就能用。它通过比例（P）、积分（I）和微分（D）三个环节来调整控制量，代码实现也比较简单：

matlab 复制代码

% 假设设定值为 setpoint，当前反馈值为 feedback
error = setpoint - feedback;
% 积分项累加
integral = integral + error * dt;
% 微分项计算
derivative = (error - previous_error) / dt;
% PID 控制输出
control_output = Kp * error + Ki * integral + Kd * derivative;
previous_error = error;

这里 Kp、Ki 和 Kd 分别是比例、积分和微分系数，通过调整这几个系数来优化控制效果。

效果对比：ADRC vs PID

我们设定默认输入为正弦路面输入，就像车辆行驶在那种有规律起伏的路面上。运行模型后，看看 ADRC 和 PID 控制下的输出：车身加速度，悬架动挠度，轮胎动变形。

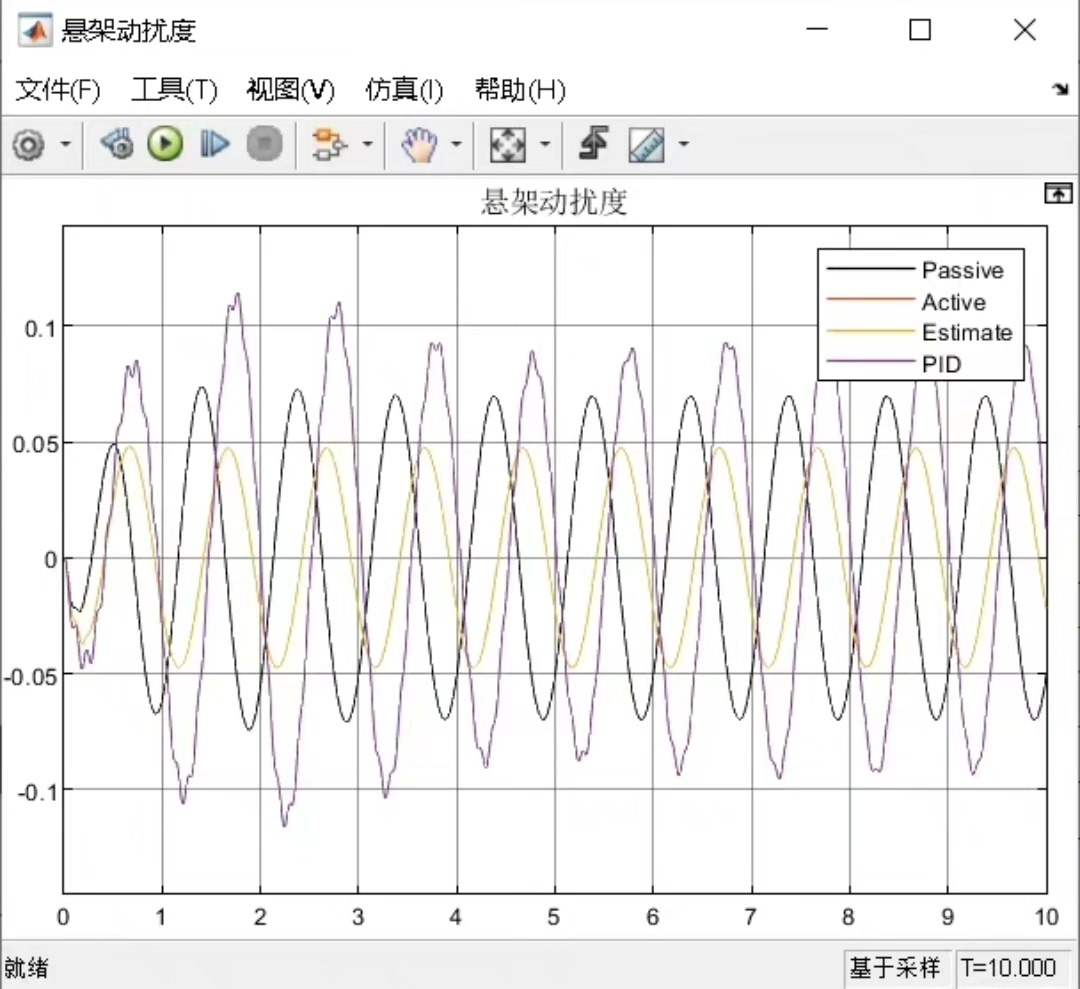
从结果上看，ADRC 控制下的车身加速度在面对正弦路面输入时，波动相对较小，能让车内乘客感觉更平稳。这是因为 ADRC 强大的抗干扰能力，能及时"应对"路面带来的各种干扰。

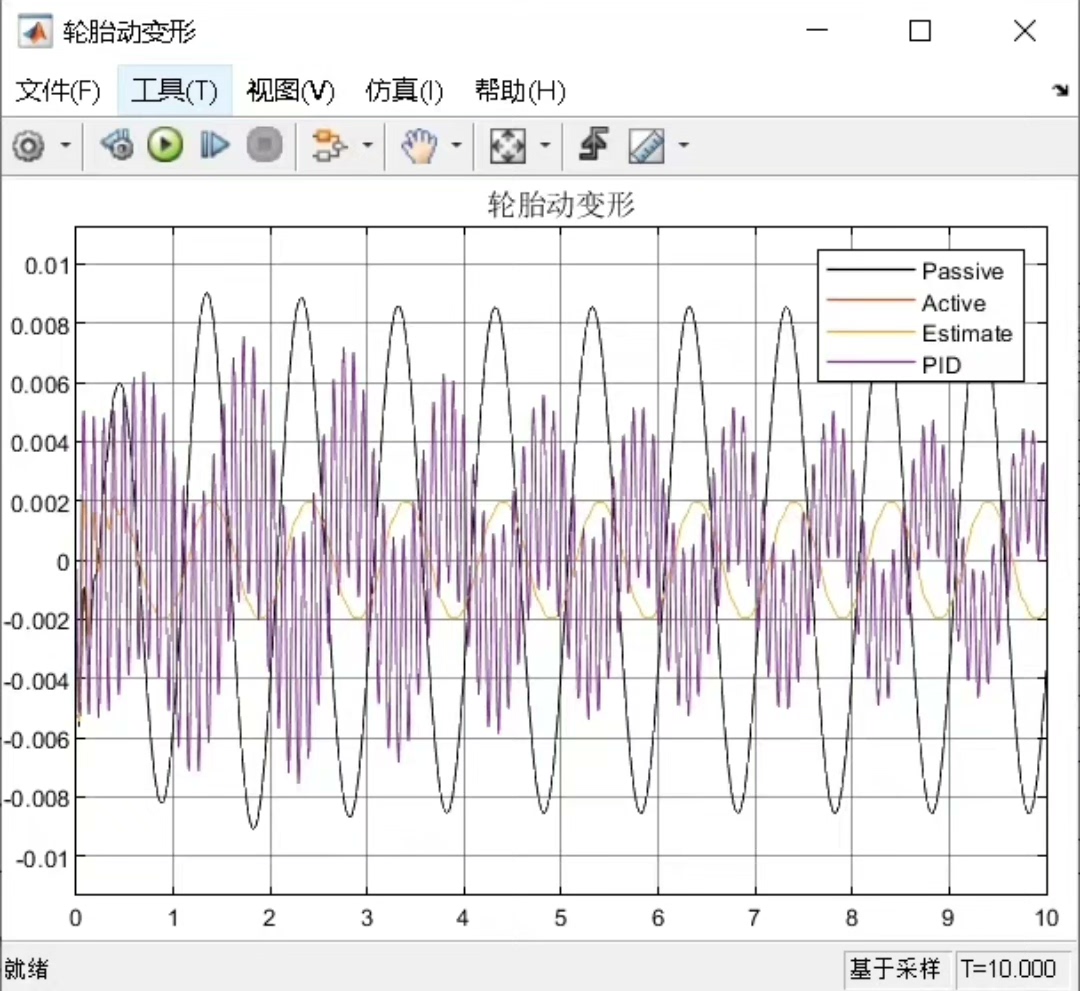
而 PID 控制呢，如果参数调得好，也能有不错的效果，但在面对一些复杂干扰时，可能就不如 ADRC 那么"淡定"了。比如在路面起伏变化较大时，PID 控制下的悬架动挠度可能会出现较大的波动，影响车辆的舒适性和操纵稳定性。

总的来说，这次 Matlab/Simulink 半车主动悬架建模之旅，让我们看到了 ADRC 和 PID 在主动悬架控制上各有千秋。ADRC 以其独特的抗干扰能力在复杂路况下表现出色，而 PID 则凭借简单易调在一些场景中也能发挥作用。希望这篇博文能给研究汽车悬架控制的小伙伴们一些启发。