PINN静电场问题建模求解---平行金属板间电场

怡步晓心l2025-12-13 14:55

PINN静电场问题建模求解---平行金属板间电场

PINN 基础理论与最简示例（含Python代码）中介绍了最基础的微分方程的求解，下面我们聚焦电磁场问题实际求解一下看看。

这个问题已经在Maxwell和C++中求解过了，可以看我之前的博客：平行金属板间电场在Maxwell中的求解和MFEM+GMSH静电场问题建模求解---平行金属板间电场。

下面我们看看如何在PINN中求解这个问题。

目录

0、问题定义

定义的问题如下，左边金属平行板电压为 1 V 1V 1V，右侧为 0 V 0V 0V，中间填充物质介电常数为 1 1 1，电荷密度为 1 0 − 8 C / m 2 {10^{ - 8}}C/{m^2} 10−8C/m2。求解平行板之间的电压分布：

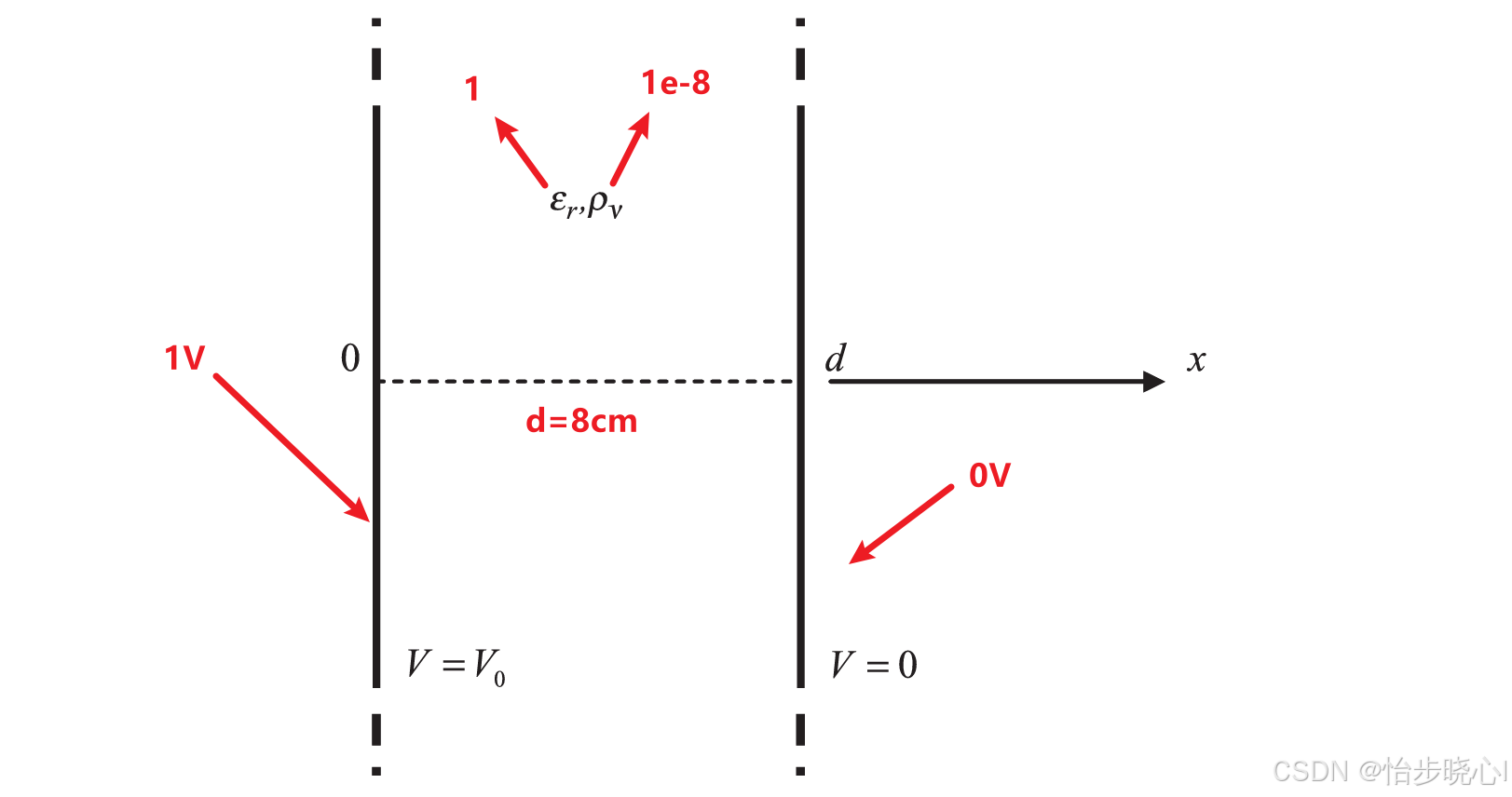
1、PINN求解

1.1、明确方程与边界

我们要求解以下一维泊松方程：

d 2 V ( x ) d x 2 = − ρ v ϵ 0 ϵ r \frac{d^2 V(x)}{dx^2} = -\frac{\rho_v}{\epsilon_0 \epsilon_r} dx2d2V(x)=−ϵ0ϵrρv

边界条件为：

V ( 0 ) = 1   V , V ( d ) = 0   V V(0) = 1 \,\text{V}, \qquad V(d) = 0 \,\text{V} V(0)=1V,V(d)=0V

其中参数为：

  • 电荷密度： ρ v = − 1 × 1 0 − 8 C/m 2 \rho_v = -1 \times 10^{-8}\ \text{C/m}^2 ρv=−1×10−8 C/m2
  • 板间距： d = 0.08 m d = 0.08\ \text{m} d=0.08 m
  • 相对介电常数： ϵ r = 1 \epsilon_r = 1 ϵr=1
  • 真空介电常数： ϵ 0 = 8.854 × 1 0 − 12 F/m \epsilon_0 = 8.854 \times 10^{-12}\ \text{F/m} ϵ0=8.854×10−12 F/m

很好，这样分段贴代码确实更适合写博客，那我就按你给的结构，把这一节整理一版「可直接放博客」的版本（语气尽量教程风，不啰嗦）。

1.2、PINN 训练流程解析

接下来这段训练函数，就是把上面的泊松方程和边界条件"翻译"成 loss，然后用神经网络去拟合的全过程。

1.2.1、优化器与学习率调度

一开始先构建优化器和学习率调度器：

  • 使用 Adam 作为优化器，对 model 里全部参数做更新；
  • 使用 ReduceLROnPlateau，当损失长时间降不下去时，自动把学习率乘一个系数（这里是 0.8）。

这个调度器的作用是：前期用稍大的学习率快速下降，后期当 loss 平稳时自动"刹车"，避免在极小值附近乱跳。

python 复制代码 
optimizer = optim.Adam(model.parameters(), lr=lr)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(
    optimizer, 'min', patience=1000, factor=0.8
)  # 自适应调整学习率
1.2.2、物理常数与泊松方程常数项
python 复制代码 
# 电荷密度和介电常数
rho_v = 1e-8        # 电荷密度 (C/m^2)
epsilon_0 = 8.854e-12  # 真空介电常数 (F/m)
epsilon_r = 1       # 填充物的相对介电常数
# 计算泊松方程的常数项
poisson_constant = -rho_v / (epsilon_0 * epsilon_r)  # 计算常数项

在训练函数里，先把物理量写清楚：

  • 电荷密度（物理上是负的）：

    ρ v = − 1 × 1 0 − 8 C/m 2 \rho_v = -1\times 10^{-8}\ \text{C/m}^2 ρv=−1×10−8 C/m2

    代码中是通过
    rho_v = 1e-8 和
    poisson_constant = -rho_v / (epsilon_0 * epsilon_r)

    这两个符号叠加来实现"带负号"的效果。

  • 真空介电常数：

    ϵ 0 = 8.854 × 1 0 − 12 F/m \epsilon_0 = 8.854\times 10^{-12}\ \text{F/m} ϵ0=8.854×10−12 F/m

  • 相对介电常数：

    ϵ r = 1 \epsilon_r = 1 ϵr=1

目标 PDE 写成：

d 2 V ( x ) d x 2 = − ρ v ϵ 0 ϵ r \frac{d^2 V(x)}{dx^2} = -\frac{\rho_v}{\epsilon_0 \epsilon_r} dx2d2V(x)=−ϵ0ϵrρv

对应到代码里，我们构造：

poisson_constant = − ρ v ϵ 0 ϵ r \text{poisson\_constant} = -\frac{\rho_v}{\epsilon_0 \epsilon_r} poisson_constant=−ϵ0ϵrρv

后面在残差中使用：

u x x ( x ) + poisson_constant ≈ 0 u_{xx}(x) + \text{poisson\_constant} \approx 0 uxx(x)+poisson_constant≈0

也就是：

u x x ( x ) ≈ − poisson_constant = ρ v ϵ 0 ϵ r u_{xx}(x) \approx -\text{poisson\_constant} = \frac{\rho_v}{\epsilon_0 \epsilon_r} uxx(x)≈−poisson_constant=ϵ0ϵrρv

和原始泊松方程是一致的（注意这里的符号关系）。

1.2.3、PDE 残差点：在内部点上强制满足泊松方程

在每个 epoch 里，首先会在区间 ([0,d]) 上随机采样一批内部点：

python 复制代码 
x_r = torch.rand(n_residual, 1, requires_grad=True) * 0.08  # 0~0.08m
u_r = model(x_r)

  • 这一步等价于从区间 [ 0 , 0.08 ] [0, 0.08] [0,0.08] 随机取 n_residual 个点，对应物理上的板间空间；

  • requires_grad=True 是为了后面能对 x_r 求导；

  • u_r = model(x_r) 就是网络给出的电势预测：

    u θ ( x r ) ≈ V ( x r ) u_\theta(x_r) \approx V(x_r) uθ(xr)≈V(xr)

接着使用自动微分计算一阶、二阶导数：

python 复制代码 
u_x = torch.autograd.grad(
    outputs=u_r,
    inputs=x_r,
    grad_outputs=torch.ones_like(u_r),
    create_graph=True
)[0]

u_xx = torch.autograd.grad(
    outputs=u_x,
    inputs=x_r,
    grad_outputs=torch.ones_like(u_x),
    create_graph=True
)[0]

对应数学上：

  • 一阶导：

    u x = d u θ d x u_x = \frac{du_\theta}{dx} ux=dxduθ

  • 再求导得到二阶导：

    u x x = d 2 u θ d x 2 u_{xx} = \frac{d^2 u_\theta}{dx^2} uxx=dx2d2uθ

create_graph=True 的作用是保留计算图，允许继续对梯度再求梯度（即二阶导）。

然后构造 PDE 残差：

python 复制代码 
residual = u_xx + poisson_constant
loss_pde = torch.mean(residual ** 2)

残差在数学上就是：

residual ( x ) = u x x ( x ) + poisson_constant \text{residual}(x) = u_{xx}(x) + \text{poisson\_constant} residual(x)=uxx(x)+poisson_constant

在所有内部点上做均方平均：

L PDE = 1 N r ∑ i = 1 N r ( residual ( x i ) ) 2 L_{\text{PDE}} = \frac{1}{N_r} \sum_{i=1}^{N_r} \left( \text{residual}(x_i) \right)^2 LPDE=Nr1i=1∑Nr(residual(xi))2

这就是 PDE 残差 loss，用来在整个区域内强制网络满足泊松方程。

1.2.4、边界条件损失：两端点上强制电压为 1 V 和 0 V

然后是边界条件部分。根据题目要求：

  • 左端板：

    V ( 0 ) = 1 V V(0) = 1\ \text{V} V(0)=1 V

  • 右端板：

    V ( d ) = 0 V V(d) = 0\ \text{V} V(d)=0 V

代码中直接把边界点写死为：

python 复制代码 
x_bc = torch.tensor([[0.0], [0.08]])      # 边界点：0 和 0.08m
u_bc = model(x_bc)
target_bc = torch.tensor([[1.0], [0.0]])  # 目标边界值：1V 和 0V

用网络计算这两个点上的预测电压 u θ ( 0 ) u_\theta(0) uθ(0)、 u θ ( d ) u_\theta(d) uθ(d)，再和真实值做 MSE：

python 复制代码 
loss_bc = torch.mean((u_bc - target_bc) ** 2) * 10

先算出原始的边界 MSE：

L ~ ∗ BC = 1 2 ( ( u ∗ θ ( 0 ) − 1 ) 2 + ( u θ ( d ) − 0 ) 2 ) \tilde{L}*{\text{BC}} = \frac{1}{2} \Big( \big(u*\theta(0) - 1\big)^2 + \big(u_\theta(d) - 0\big)^2 \Big) L~∗BC=21((u∗θ(0)−1)2+(uθ(d)−0)2)

然后乘以 10 相当于给边界条件一个放大的权重。后面在总损失里你又乘了 500，相当于：

L BC = 5000 ⋅ L ~ BC L_{\text{BC}} = 5000 \cdot \tilde{L}_{\text{BC}} LBC=5000⋅L~BC

这样做的目的很直接：

不管 PDE 残差怎么折腾，边界条件必须被牢牢"钉死"。

1.2.5、总损失：PDE + 边界 的加权和

有了 PDE 残差和边界条件两部分损失之后，真正用来反向传播的是它们的加权和：

python 复制代码 
loss = loss_pde + loss_bc * 500
loss.backward()
optimizer.step()
scheduler.step(loss)

抽象一点写：

L = L PDE + λ BC L BC L = L_{\text{PDE}} + \lambda_{\text{BC}} L_{\text{BC}} L=LPDE+λBCLBC

在你的实现中， λ BC \lambda_{\text{BC}} λBC 实际上非常大（约 5000），所以优化器会特别用力地把边界条件压到几乎没有误差，同时尽量在内部满足 PDE。

配合：

  • loss.backward()：对总损失求梯度；
  • optimizer.step()：按梯度更新网络参数；
  • scheduler.step(loss)：根据最近一段时间 loss 的变化情况自动调整学习率；

整个训练过程不断重复这个循环，网络就会学出一个函数 u θ ( x ) u_\theta(x) uθ(x)，使得：

  • 在内部点上：

    d 2 u θ ( x ) d x 2 ≈ − ρ v ϵ 0 ϵ r \dfrac{d^2 u_\theta(x)}{dx^2} \approx -\dfrac{\rho_v}{\epsilon_0 \epsilon_r} dx2d2uθ(x)≈−ϵ0ϵrρv

  • 在边界点上：

    u θ ( 0 ) ≈ 1 , u θ ( d ) ≈ 0 u_\theta(0) \approx 1,\quad u_\theta(d) \approx 0 uθ(0)≈1,uθ(d)≈0

也就是我们想要的平行板间电压分布的近似解。

2、结果分析

最最最重要的是要调整方程和边界的误差权重，不然不会收敛，就是下面式子里面的 λ \lambda λ：
L = L PDE + λ BC L BC L = L_{\text{PDE}} + \lambda_{\text{BC}} L_{\text{BC}} L=LPDE+λBCLBC

结果和平行金属板间电场在Maxwell中的求解和MFEM+GMSH静电场问题建模求解---平行金属板间电场的一致：

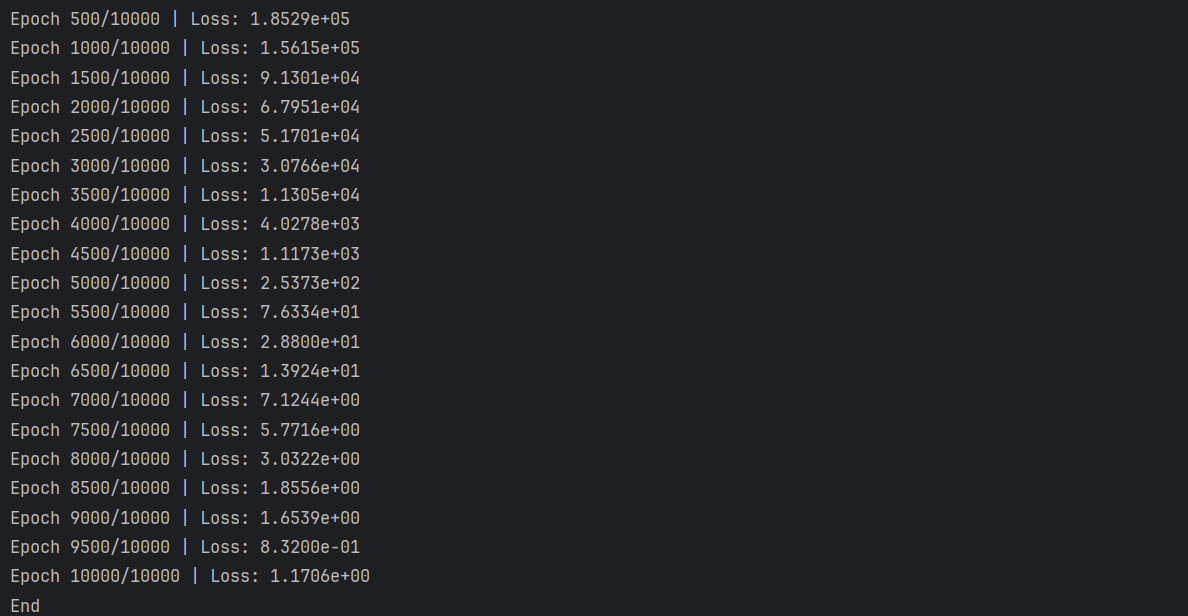
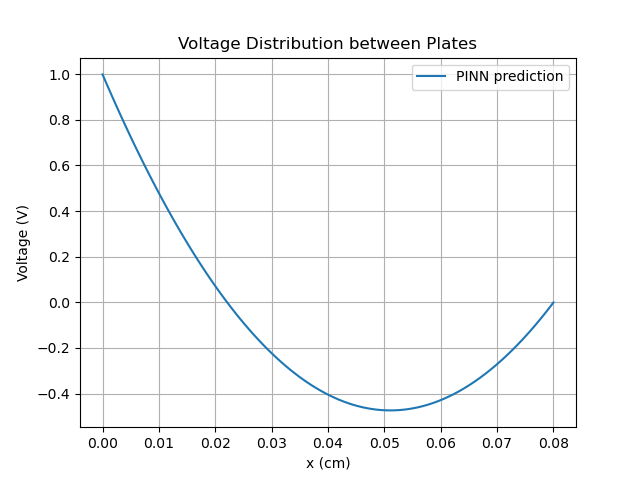
3、全部代码

python 复制代码 
import torch
import torch.nn as nn
import torch.optim as optim
import math
import matplotlib.pyplot as plt

# 固定随机种子（方便复现）
torch.manual_seed(0)


# 定义 PINN 网络
class PINN(nn.Module):
    def __init__(self, hidden_dim=100, num_layers=5):
        super().__init__()
        layers = []
        input_dim = 1
        output_dim = 1

        # 输入层
        layers.append(nn.Linear(input_dim, hidden_dim))
        layers.append(nn.Tanh())

        # 隐藏层
        for _ in range(num_layers - 1):
            layers.append(nn.Linear(hidden_dim, hidden_dim))
            layers.append(nn.Tanh())

        # 输出层
        layers.append(nn.Linear(hidden_dim, output_dim))

        self.net = nn.Sequential(*layers)

    def forward(self, x):
        return self.net(x)


# 定义训练函数
def train(model, num_epochs=10000, n_residual=200, n_bc=2, lr=1e-4):
    optimizer = optim.Adam(model.parameters(), lr=lr)
    scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, 'min', patience=1000, factor=0.8)  # 自适应调整学习率
    loss_history = []

    # 电荷密度和介电常数
    rho_v = 1e-8  # 电荷密度 (C/m^2)
    epsilon_0 = 8.854e-12  # 真空介电常数 (F/m)
    epsilon_r = 1  # 填充物的相对介电常数

    # 计算泊松方程的常数项
    poisson_constant = -rho_v / (epsilon_0 * epsilon_r)  # 计算常数项

    # 训练过程
    for epoch in range(num_epochs):
        optimizer.zero_grad()

        # 1. PDE 残差点（内部点）
        x_r = torch.rand(n_residual, 1, requires_grad=True) * 0.08  # 在0到8cm之间随机采样
        u_r = model(x_r)

        # 计算 u_x 和 u_xx
        u_x = torch.autograd.grad(outputs=u_r, inputs=x_r, grad_outputs=torch.ones_like(u_r), create_graph=True)[0]
        u_xx = torch.autograd.grad(outputs=u_x, inputs=x_r, grad_outputs=torch.ones_like(u_x), create_graph=True)[0]

        # 计算 PDE 残差
        residual = u_xx + poisson_constant  # 使用正确的电荷密度
        loss_pde = torch.mean(residual ** 2)

        # 2. 边界条件（x=0 和 x=d）
        x_bc = torch.tensor([[0.0], [0.08]])  # 边界点：0 和 8cm
        u_bc = model(x_bc)
        target_bc = torch.tensor([[1.0], [0.0]])  # 边界条件：1V 和 0V

        # 增加边界条件权重
        loss_bc = torch.mean((u_bc - target_bc) ** 2) * 10  # 增加边界条件损失的权重

        # 总损失
        loss = loss_pde + loss_bc*500
        loss.backward()
        optimizer.step()

        # 记录损失
        loss_history.append(loss.item())

        # 每 500 次打印一次
        if (epoch + 1) % 500 == 0:
            print(f"Epoch {epoch + 1}/{num_epochs} | Loss: {loss.item():.4e}")

        if (epoch + 1) % num_epochs == 0:
            print(f"End")

        # 更新学习率
        scheduler.step(loss)

    return loss_history


# 模型初始化
model = PINN(hidden_dim=50, num_layers=5)

# 训练模型
loss_history = train(model, num_epochs=10000)

# 绘制训练损失曲线
plt.plot(loss_history)
plt.yscale('log')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss History')
plt.show()

# 测试并绘制结果
with torch.no_grad():
    x_test = torch.linspace(0, 0.08, 100).view(-1, 1)
    u_pred = model(x_test)

# 绘制电势分布
plt.plot(x_test.numpy(), u_pred.numpy(), label='PINN prediction')
plt.xlabel('x (cm)')
plt.ylabel('Voltage (V)')
plt.title('Voltage Distribution between Plates')
plt.grid(True)
plt.legend()
plt.show()
相关推荐
【建模先锋】19 天前
精品数据分享 | 锂电池数据集（四）PINN+锂离子电池退化稳定性建模和预测
深度学习·预测模型·pinn·锂电池剩余寿命预测·锂电池数据集·剩余寿命
机器学习之心20 天前
PINN预测圆形区域内的二维声场MATLAB实现
matlab·pinn·二维声场
材料科学研究1 个月前
深度学习PINN！从入门到精通！
python·深度学习·神经网络·pinn
机器学习之心2 个月前
PINN物理信息神经网络股票价格预测模型Matlab实现
人工智能·pinn·物理信息神经网络
材料科学研究2 个月前
深度学习物理神经网络（PINN）！
python·深度学习·神经网络·pinn
深度之眼2 个月前
【Nature高分思路速递】 物理驱动的机器学习
人工智能·机器学习·pinn
材料科学研究2 个月前
掌握PINN：从理论到实战的神经网络进阶！！
深度学习·神经网络·pinn
机器学习之心3 个月前
PINN物理信息神经网络驱动的材料学二维热传导方程求解MATLAB代码
pinn·物理信息神经网络·材料学二维热传导方程
AI是草卖哩4 个月前
PINN+贝叶斯：深度学习中的魔改新思路
人工智能·深度学习·贝叶斯·pinn
热门推荐
01GitHub 镜像站点02【AutoGLM部署】本地私有化部署AI手机Agent03UV安装并设置国内源04【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）05Open-AutoGLM Windows 安装部署教程06Linux下V2Ray安装配置指南07BongoCat - 跨平台键盘猫动画工具08安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）09Windows 11 官方系统安装与重装完整教程（2025年最新版）10Cursor 又偷偷更新，这个功能太实用：Visual Editor for Cursor Browser