学习目标
-
理论构建能力:深入理解AI for PDEs的数学原理,能够独立推导强形式(Strong Form)与能量形式(Energy Form)的转换机制,并掌握超参数选取的理论依据。
-
模型搭建与优化:
◦ 熟练搭建基于经典MLP和前沿KAN(Kolmogorov-Arnold Networks)架构的PINNs模型。
◦ 掌握深度算子网络(DeepONet)、傅里叶神经算子(FNO)及Transformer形式神经算子的搭建技巧。
-
复杂力学问题求解:能够运用深度能量法(Deep Energy Method)和VINO等方法,解决线弹性、超弹性、塑性力学中的正问题。
-
攻克反问题与断裂难题:掌握利用AI识别弹性模量场、本构方程及缺陷检测的反问题求解策略;并能应用扩展深度能量法解决离散与连续(相场)断裂力学问题。
-
前沿科研落地:具备复现顶刊算法的能力,并能将其迁移应用到自己的科研课题中,为发表高水平论文打下基础
具备的基础知识:
- 具备的基础知识:
精通:高等数学,线性代数,有限元,弹性力学。
熟练:变分原理,张量分析,数值分析,连续介质力学(主要是包括弹性,塑性,超弹性,和断裂力学)。
略懂:数理统计,机器学习,深度学习。不需要具备其他特殊基础知识!把所有精力都放在听课上,授课老师会在课堂中讲的非常清楚。
- 提前安装的软件:
Anaconda的spyder,
python需要安装pytorch库,最好是GPU版本。
讲师介绍
PINN专题主讲老师:来自国内TOP2高校,长期从事 AI for Science 研究,重点聚焦 AI for PDEs 在固体力学中的理论、方法与应用。系统掌握固体力学的理论基础、实验方法与数值计算技术,在物理建模与机器学习方法的深度融合方面具有扎实积累。已在计算力学领域顶级期刊 Computer Methods in Applied Mechanics and Engineering (CMAME)、International Journal for Numerical Methods in Engineering (IJNME) 等发表论文20余篇。担任30余本高水平SCI期刊的审稿人,包括 Journal of the Mechanics and Physics of Solids (JMPS) 等国际顶尖期刊。
专题一:PINN固体力学及断裂力学
第一天:AI for PDEs 整体概述与理论基石 (侧重理论推导与宏观视野)
本专题旨在为后续的上机实操打下坚实的理论基础。
• 上午:发展脉络与趋势
◦ AI for Science 概览与智能计算力学发展历程汇报。
◦ 案例演示: 展示AI在经典力学方程求解中相比传统有限元的效率优势。
• 下午:核心理论手推(板书教学)
◦ 重点推导: 偏微分方程的强形式残差构建 vs 变分原理下的能量形式转换。
◦ 关键理论: 损失函数(Loss Function)的设计原则与超参数自适应调整策略。
◦ 方法论体系: PINNs、Operator Learning、Physics-Informed Neural Operators 区别与联系。
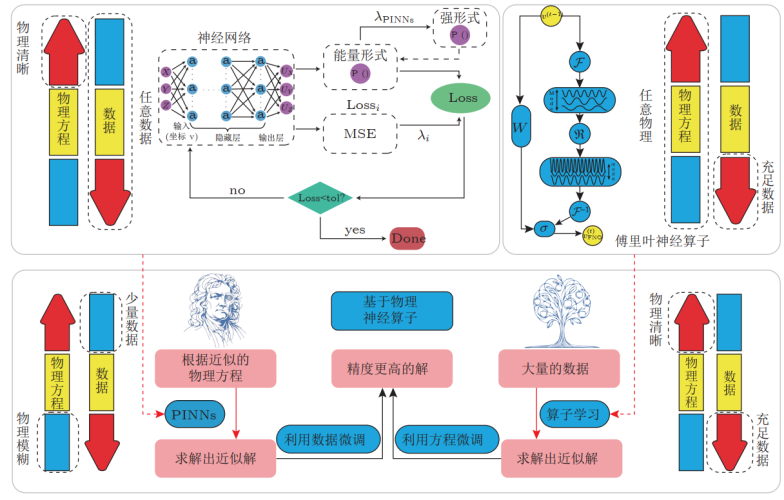
第二天:PINNs 强形式基础架构与进阶模型 (聚焦核心架构搭建)
• 核心内容:
◦ 基于MLP(多层感知机)的标准PINNs搭建。
◦ 基于KAN(Kolmogorov-Arnold Networks)的新型PINNs实现。
• 实战案例 (Case Studies):
◦ 案例 1: 求解高频与低频震荡问题的对比实验(解决谱偏差问题)。
◦ 案例 2: 复杂几何边界下的热传导或简单弹性问题模拟。
◦ 案例3: 热传导问题反问题的求解
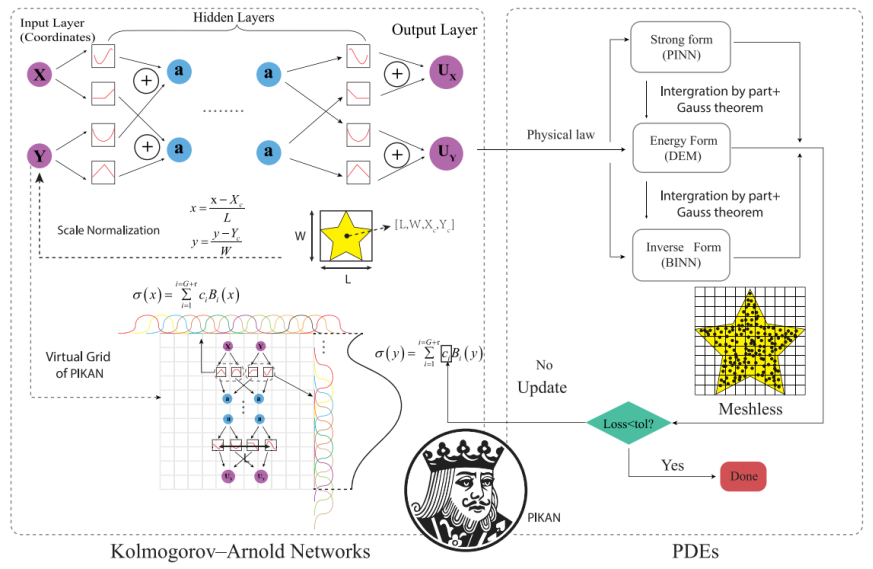
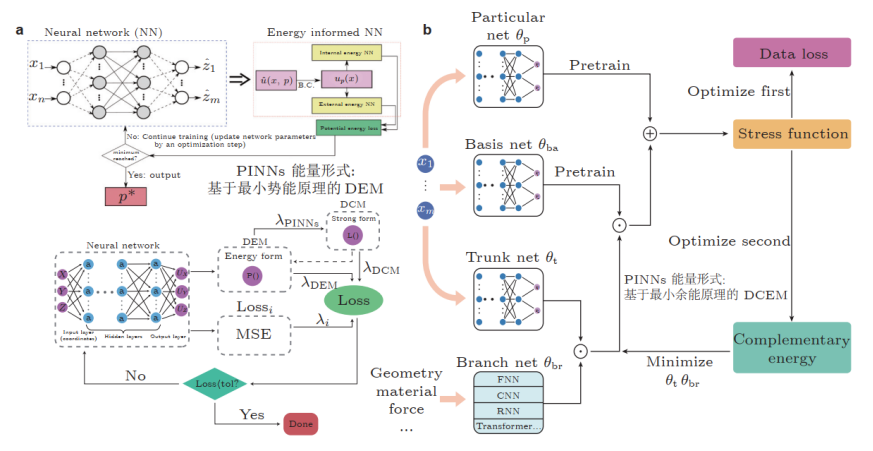
第三天:PINNs 能量形式在固体力学中的深度应用 (聚焦能量法与反问题)
• 核心内容:
◦ 深度能量法 (DEM) 与深度余能法 (DCEM) 的代码实现。
◦ 迁移学习技术在加速收敛中的应用。
• 实战案例 (Case Studies):
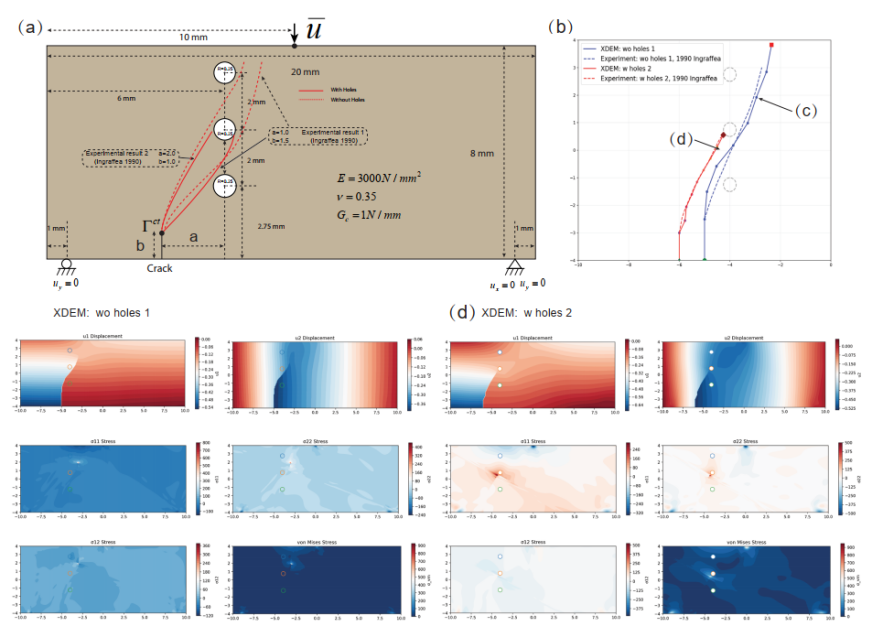
◦ 案例1: 线弹性带孔方板应力集中实验
◦ 案例2: 超弹性材料(如橡胶)在由大变形引发的非线性响应模拟。
◦ 案例3: 余能原理在普朗特和Airy应力函数上的应用
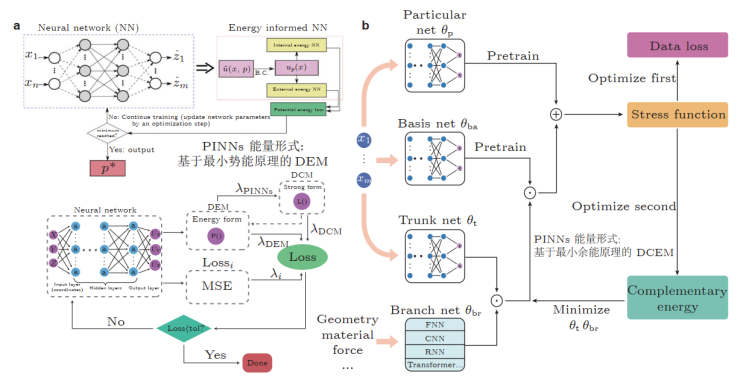
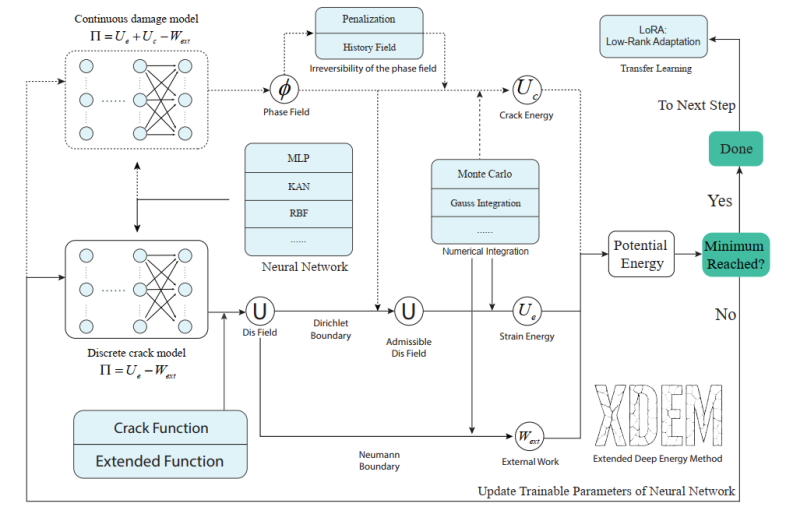
第四天:PINNs 在断裂力学中的前沿挑战 (聚焦离散与连续断裂模型)
• 核心内容:
◦ 离散断裂力学:基于应力强度因子(SIFs)的计算策略。
◦ 连续断裂力学:基于相场断裂(Phase Field)理论的AI求解。
• 实战案例 (Case Studies):
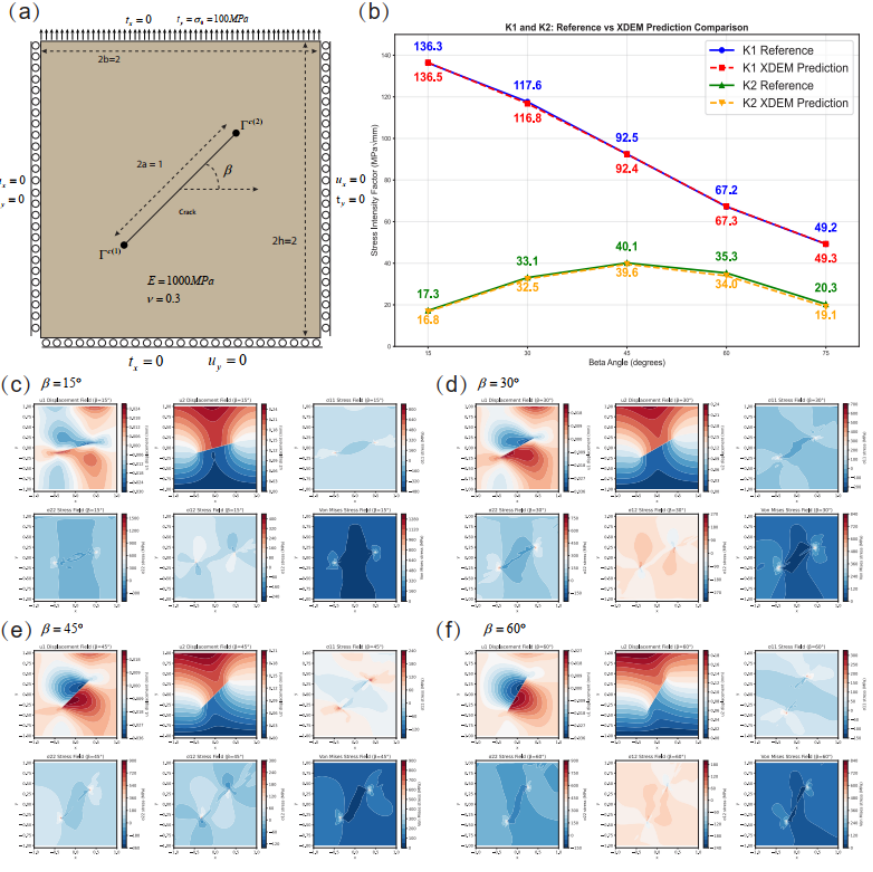
◦ 案例1: 利用扩展深度能量法计算裂纹尖端的奇异性应力场。
◦ 案例2: 模拟矩形板在拉伸载荷下的裂纹萌生与扩展路径(相场云图复现)。
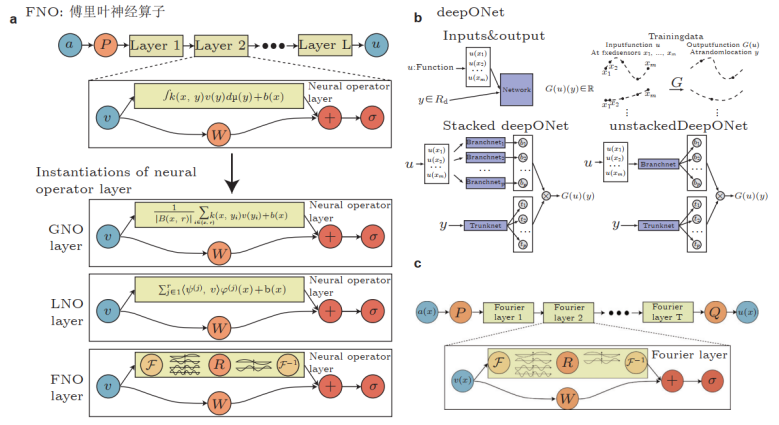
第五天:数据驱动和物理驱动的算子学习 (Operator Learning) (聚焦函数空间映射)
• 核心内容:
◦ DeepONet、FNO(傅里叶神经算子)及Transformer神经算子的模型搭建。
◦ 强形式 PINO (Physics-Informed Neural Operator)。
◦ 能量形式 VINO (Variational Neural Operator)。
• 实战案例 (Case Studies):
◦ 案例1: DeepONet应用------快速预测不同载荷条件下的应力函数分布。
◦ 案例2: FNO应用------复合材料多尺度计算中的均匀化问题(直接预测有效属性)。
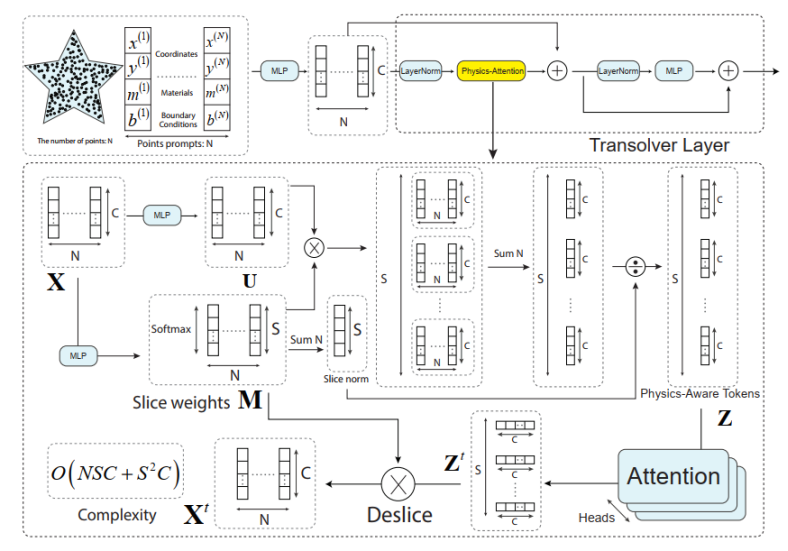
◦ 案例3: Transformer算子在标准力学Benchmark基准题上的性能评估。
◦ 案例4: VINO实战------仅利用物理方程训练网络,直接求解弹性力学边值问题。
◦ 案例5: Transformer算子进阶------处理超弹性材料的复杂非线性本构关系。
PINN固体力学及断裂力学专题
2026.04.13---2026.04.17 (晚上19:00-22:00)
2026.04.20---2026.04.24 (晚上19:00-22:00)
腾讯会议 线上授课(共五天课程 提供全程视频回放和课程群答疑)