MATLAB 中提取冲击信号的解卷积方法探索

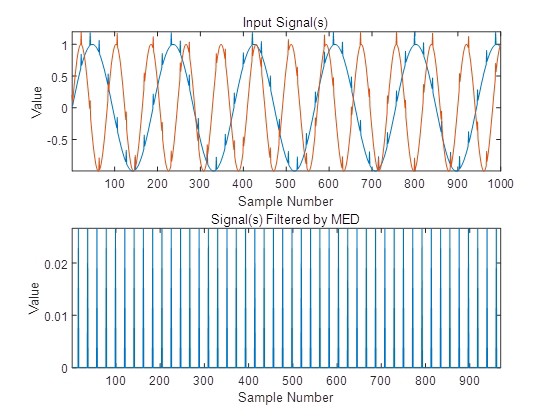
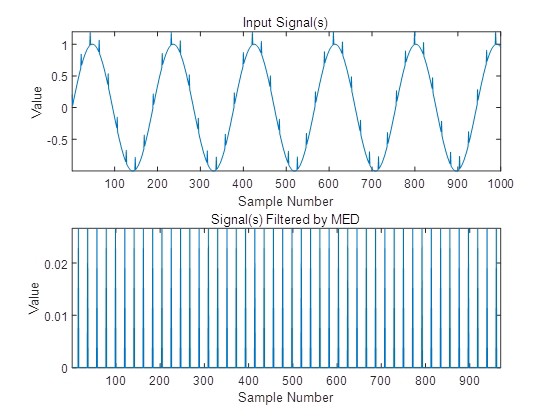
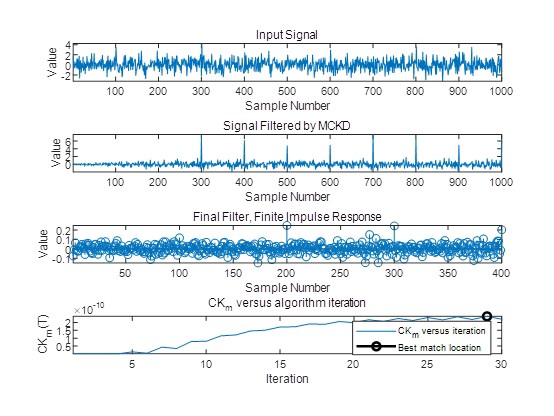
MATLAB环境下用于提取冲击信号的几种解卷积方法卷积混合考虑了信号的时延，每一个单独源信号的时延信号都会和传递路径发生一次线性瞬时混合；解卷积的过程就是找一个合适的滤波器，进行反卷积运算，得到源信号的近似解。声音不可避免的会发生衍射、反射等现象，所以，源声信号及其时延信号在传递过程中会发生卷积然后到达麦克风。所以，卷积模型更符合实际工程问题，利用解卷积思路用于振动、声音信号的信号处理以及齿轮、轴承的故障特征增强的有最小熵解卷积、最大相关峭度解卷积、多点最优最小熵解卷积调整、最大二阶循环平稳盲解卷积等方法。程序运行环境为MATLAB R2018A，包含用于提取冲击信号的几种解卷积方法，可用于一维信号处理与机械故障诊断，也可用于金融时间序列，地震信号，机械振动信号，语音信号，声信号等一维时间序列信号。几种方法如下： [1]最大相关峭度解卷积 [2]二维最小熵解卷积 [3]多点最优最小熵解卷积 [4]最小熵解卷积d-范数精确解方法

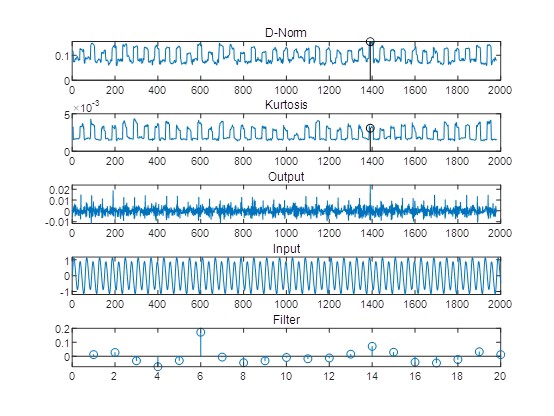
在 MATLAB 的奇妙世界里，处理信号问题总是充满乐趣与挑战。今天咱们来聊聊用于提取冲击信号的几种解卷积方法。

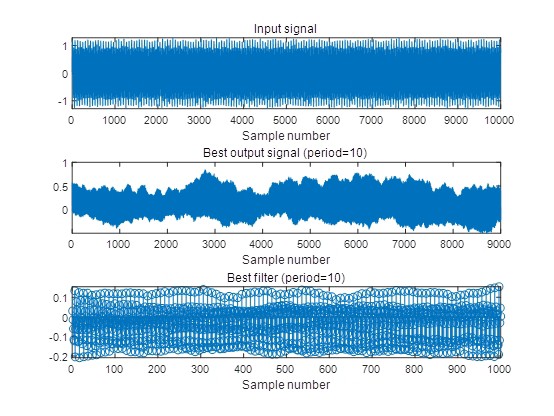
首先得知道，卷积混合这事儿考虑了信号的时延。想象一下，每个单独源信号的时延信号，就像一个个小伙伴，它们会分别和传递路径来一场线性瞬时混合的"聚会"。而解卷积呢，就像是给这场聚会找一个"神奇滤镜"------合适的滤波器，通过反卷积运算，找到源信号的近似解。

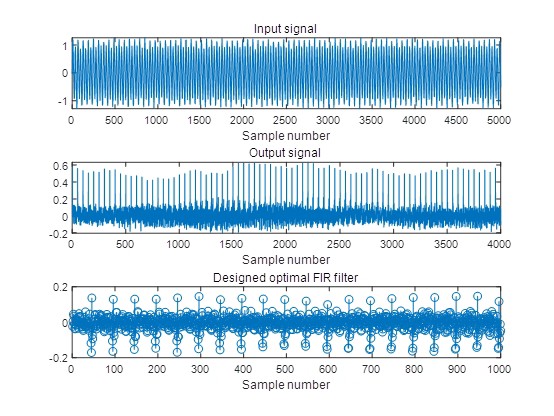
为啥这很重要呢？就拿声音来说，在传播过程中，衍射、反射等现象就像调皮的小精灵，让源声信号及其时延信号在传递过程中玩起了卷积游戏，最后才到达麦克风。所以，卷积模型在实际工程问题里那是相当贴合实际的。利用解卷积思路，在振动、声音信号处理，还有齿轮、轴承故障特征增强等方面都能大显身手。咱们今天就着重看看在 MATLAB R2018A 环境下，用于提取冲击信号的几种解卷积方法，它们对一维信号处理、机械故障诊断，甚至金融时间序列、地震信号、机械振动信号、语音信号和声信号等一维时间序列信号都很有用呢。

最大相关峭度解卷积

最大相关峭度解卷积旨在最大化输出信号的峭度与参考信号之间的相关性。通过优化滤波器，使得输出信号尽可能地接近理想的冲击信号。在 MATLAB 里，大概的实现思路可以像下面这样（这里只是示意性代码，实际应用可能需根据具体情况调整）：

matlab 复制代码

% 假设已经有混合信号 x 和初始滤波器 h0
x = [1 2 3 4 5]; % 示例混合信号
h0 = [0.1 0.2]; % 初始滤波器

% 定义相关参数
num_iterations = 100;
step_size = 0.01;

for k = 1:num_iterations
    y = conv(x, h0); % 卷积运算
    % 这里可能需要计算峭度和相关性，假设已有计算函数
    kurtosis_y = calculate_kurtosis(y); 
    corr_y_ref = calculate_correlation(y, reference_signal); 
    % 根据峭度和相关性调整滤波器
    h0 = h0 + step_size * (calculate_gradient(kurtosis_y, corr_y_ref)); 
end

在这段代码里，首先定义了混合信号 x 和初始滤波器 h0。然后设定迭代次数 numiterations**和步长 step size。在每次迭代中，先对信号和滤波器进行卷积得到输出 y，接着计算 y 的峭度和与参考信号的相关性，最后根据这些结果调整滤波器 h0，让它朝着能更好提取冲击信号的方向变化。

二维最小熵解卷积

二维最小熵解卷积是将最小熵原理拓展到二维空间。这种方法在处理一些具有二维特性的信号时特别有效，比如某些图像相关的信号处理。在 MATLAB 实现时，我们可能要处理二维矩阵相关的操作：

matlab 复制代码

% 假设已有二维混合信号矩阵 X
X = rand(10, 10); % 示例二维混合信号矩阵

% 初始化二维滤波器 H
H = rand(3, 3);

% 进行二维卷积操作
Y = conv2(X, H);

% 计算二维输出信号的熵
entropy_Y = calculate_2d_entropy(Y);

% 这里可以根据熵的值去迭代优化滤波器 H，假设已有优化函数
H = optimize_filter_2d(X, H, entropy_Y);

在这段代码里，首先生成一个二维混合信号矩阵 X 和初始化二维滤波器 H。通过 conv2 函数进行二维卷积得到输出 Y，接着计算 Y 的二维熵，最后根据熵值利用自定义的优化函数来调整二维滤波器 H。

多点最优最小熵解卷积

多点最优最小熵解卷积则是从多个点的角度出发，综合考虑多个位置的信号情况，来优化解卷积过程。下面简单示意一下 MATLAB 代码：

matlab 复制代码

% 假设有一维混合信号 x
x = [1 2 3 4 5 6 7 8 9 10];

% 定义多个点的位置
points = [2 5 8];

% 初始化滤波器 h
h = [0.1 0.2];

for point in points
    % 提取每个点附近的局部信号
    local_x = get_local_signal(x, point); 
    y = conv(local_x, h);
    entropy_y = calculate_entropy(y);
    % 根据熵值调整滤波器 h
    h = update_filter(h, entropy_y); 
end

这段代码里，先定义了一维混合信号 x 和多个点的位置 points，然后初始化滤波器 h。对每个点，先提取该点附近的局部信号，接着进行卷积并计算熵，最后根据熵来调整滤波器 h，从多个点的局部信息综合优化解卷积。

最小熵解卷积 d - 范数精确解方法

这种方法通过寻找最小熵解卷积的 d - 范数精确解来优化滤波器。MATLAB 实现可能如下：

matlab 复制代码

% 假设已有混合信号 x
x = [1 2 3 4 5];

% 定义 d - 范数相关参数
d = 2;

% 计算最小熵解卷积 d - 范数精确解得到滤波器 h
h = calculate_d_norm_min_entropy(x, d);

这里假设已经有混合信号 x，定义了 d - 范数的参数 d，然后通过自定义函数 calculated normminentropy 来计算得到滤波器 h，从而实现基于最小熵解卷积 d - 范数精确解的信号处理。

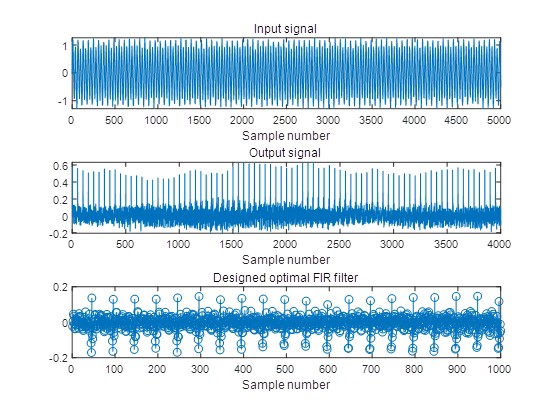
以上就是 MATLAB 环境下用于提取冲击信号的几种解卷积方法啦，每一种都有其独特的思路和应用场景，希望能给大家在信号处理的探索之路上带来一些启发。