C++的map和set

关联式容器

序列式容器 (Sequence Containers)

元素按线性顺序排列
通过下标或迭代器访问元素

关联式容器 (Associative Containers)

元素按特定顺序排列（哈希表、红黑树）
通过键(Key)或迭代器访问元素
提供快速的查找功能

键值对

键值对用来表示具有一一对应关系的一种结构，该结构中一般只包含两个成员变量key和value，key代表键值，value表示与key对应的信息。
SGI-STL对pair的定义

cpp 复制代码

template <class T1, class T2>
struct pair
{

    T1 first;
    T2 second;

    pair(): first(T1()), second(T2())
    {}

    pair(const T1& a, const T2& b): first(a), second(b)
    {}
};

树形结构的关联式容器

根据应用场景的不同，STL总共实现了两种不同结构的关联式容器：树型结构与哈希结构。
树型结 构的关联式容器主要有四种：map、set、multimap、multiset。这四种容器的共同点是使用平衡二叉搜索树(即红黑树)作为其底层结构。

set

与map/multimap不同，map/multimap中存储的元素是真正的键值对<key, value>，set中的元素实际是<value, value>（也可理解为<key，key>）构成的键值对。
set中插入元素时，只需要传参value即可。
set中的元素不可以重复(因此可以使用set进行去重)。
使用set的迭代器遍历set中的元素，可以得到有序序列，底层是因为红黑树是搜索树，中序是有序的
set中的元素默认按照小于来比较，最后迭代器遍历就是升序，换句话说底层红黑树此时中序是升序的
set中查找某个元素，时间复杂度为：log2n
set中的元素不允许修改，因为修改会破坏搜索树的结构
set中的底层使用平衡二叉搜索树(红黑树)来实现

set的使用

模板参数列表

第一个模板参数可以认为是key，也可以认为是value，最后set底层元素是<T ,T>
第二个模板参数是比较规则，可以认为是底层红黑树中序的顺序，如果是小于比较那红黑树的中序就是升序，如果是大于比较那红黑树的中序就是降序
第三个模板参数是空间配置器类型

构造函数

默认构造，初始化一个空set

begin

返回一个迭代器，迭代器中的红黑树节点指针指向红黑树最小节点

end

返回红黑树中最大节点的下一个位置的迭代器，可以理解为迭代器中红黑树节点指针是nullptr

empty

判断set是不是为空，也就是红黑树是不是为空

size

返回set中元素个数，即红黑树中节点个数

insert

往set中插入元素，value_type就是key的类型，如果已经存在，那就返回元素对应的迭代器，还有false表示插入失败

假如不存在，那就插入，然后返回插入元素的迭代器，还有true表示插入成功

erase

**第一个erase函数：**根据迭代器先查找，然后删除迭代器指向的元素

**第二个erase函数：**删除所有键为val的元素，返回删除元素个数

swap

set中只有一个成员红黑树，交换两个set其实就是交换红黑树

clear

清理底层红黑树所有节点

find

查找键为val的元素，如果找不到就返回end()，如果找到了就返回元素对应的迭代器

count

返回set中键为val的元素的个数，因为set中不允许元素重复，所以这个返回值只会是0或1

set的模拟实现

set模拟实现

map

map中的的元素是键值对，即<key，value>
map中的key是唯一的，并且不能修改，不然就破坏了搜索树的结构
默认按照小于的方式对key进行比较来对元素进行排序
map中的元素如果用迭代器去遍历，可以得到一个有序的序列，其实就是红黑树的中序遍历
map的底层为二叉平衡搜索树(红黑树)，查找效率为log2 N
支持operator[ ]操作符，operator[ ]中实际进行的是一个插入查找。

map的使用

模板参数列表

第一个模板参数可以认为是key，也就是键的类型
第二个模板参数是value，也就是值的类型，最终map底层元素的类型其实就是<key，value>
第三个模板参数是比较规则，如果是小于比较那红黑树的中序就是升序，如果是大于比较那红黑树的中序就是降序
第四个模板参数是空间配置器类型

构造函数

默认构造，初始化一个空map

begin

返回一个迭代器，迭代器中的红黑树节点指针指向红黑树最小节点

end

返回红黑树中最大节点的下一个位置对应的迭代器，可以理解为迭代器中红黑树节点指针是nullptr

empty

判断map是不是为空，也就是红黑树是不是为空

size

返回map中元素个数，即红黑树中节点个数

insert

往map中插入元素，注意这里value_type是pair<Key，Value>，如果已经存在，那就返回元素对应的迭代器，还有false表示插入失败

假如不存在，那就插入，然后返回插入元素的迭代器，还有true表示插入成功

erase

**第一个erase函数：**根据迭代器先查找，然后删除迭代器指向的元素

**第二个erase函数：**删除所有键为k 的元素，返回删除元素个数

swap

map中只有一个成员红黑树，交换两个map其实就是交换红黑树

clear

清理底层红黑树所有节点

find

查找键为k 的元素，如果找不到就返回end()，如果找到了就返回元素对应的迭代器

count

返回map中键为k的元素的个数，因为map中不允许元素重复，所以这个返回值只会是0或1

operator[]

map的operator[ ]会返回键为k的元素对应的值value的引用。这个函数是一个插入查询函数，该函数会先尝试插入<k, Value()>的元素，如果键为k的元素已存在，那就插入失败，insert会返回已存在元素的迭代器还有false，operator[ ]利用迭代器返回已存在元素对应值的引用，如果插入成功，insert就就返回新插入元素的迭代器和true，然后operator[ ]利用迭代器返回元素中值的引用

cpp 复制代码

(*((this->insert(make_pair(k,mapped_type()))).first)).second

map的模拟实现

multiset

multiset中的元素是<value, value>的键值对，其底层结构还是红黑树
与set的区别是，multiset中的元素可以重复，set是中元素是唯一的，multiset每次插入必定成功，而set插入时如果元素已经存在则会插入失败
使用迭代器对multiset中的元素进行遍历，可以得到有序的序列
multiset中的元素不能修改
在multiset中找某个元素，时间复杂度为log2n

multimap

multimap和map的唯一不同就是：map中的键key是唯一的，而multimap中键key是可以****重复的。

multimap中的key是可以重复的，multimap中的元素是<key，value>
multimap中的元素默认根据key按小于的顺序来进行排序
multimap中没有重载operator[ ]操作，因为multimap中允许key相同的元素存在，而这几个元素的值可以不同，这时operator[ ]要返回哪一个元素的值的引用呢，所以multimap中直接不提供operator[ ]

AVL树

AVL树的概念

AVL树是在二叉搜索树的基础上添加了平衡因子，用来使搜索树保持平衡，对于一颗AVL树，要么是一颗空树，要么其每个节点都满足左右子树高度差不超过1

AVL树节点的定义

cpp 复制代码

template<class T>
struct AVLTreeNode
{
 AVLTreeNode(const T& data)
     : _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr)
 , _data(data), _bf(0)
 {}
 AVLTreeNode<T>* _pLeft;   // 该节点的左孩子
 AVLTreeNode<T>* _pRight;  // 该节点的右孩子
 AVLTreeNode<T>* _pParent; // 该节点的双亲
 T _data;
 int _bf;                  // 该节点的平衡因子
};

AVL树的插入

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也是二叉搜索树。AVL树的插入过程可以分为两步：

按照二叉搜索树的方式插入新节点
依次往上调整节点的平衡因子

cpp 复制代码

bool Insert(const T& data)
{
    // 1. 先按照二叉搜索树的规则将节点插入到AVL树中
    // ...
    
    // 2. 新节点插入后，AVL树的平衡性可能会遭到破坏，此时就需要更新平衡因子，并检测是否
    //破坏了AVL树的平衡性
    
 /*
 pCur插入后，pParent的平衡因子一定需要调整，在插入之前，pParent
 的平衡因子分为三种情况：-1，0, 1, 分以下两种情况：
  1. 如果pCur插入到pParent的左侧，只需给pParent的平衡因子-1即可
  2. 如果pCur插入到pParent的右侧，只需给pParent的平衡因子+1即可
  
 此时：pParent的平衡因子可能有三种情况：0，正负1， 正负2
  1. 如果pParent的平衡因子为0，说明插入之前pParent的平衡因子为正负1，插入后被调整
成0，此时子树的高度没有变化，所以无需继续往上调整
  2. 如果pParent的平衡因子为正负1，说明插入前pParent的平衡因子一定为0，插入后被更
新成正负1，此时该子树的高度增加，所以需要往上继续调整
  3. 如果pParent的平衡因子为正负2，则pParent的平衡因子违反平衡树的性质，需要对其进
行旋转处理
 */

 while (pParent)
 {
        // 更新双亲的平衡因子
     if (pCur == pParent->_pLeft)
         pParent->_bf--;
     else
         pParent->_bf++;
     // 更新后检测双亲的平衡因子
     if (0 == pParent->_bf)
     {    
            break;
     }
     else if (1 == pParent->_bf || -1 == pParent->_bf)
     {
              // 插入前父节点的平衡因子是0，插入后父节点的平衡因为为1 或者 -1 ，说明以父节点
    为根的二叉树的高度增加了一层，因此需要继续向上调整
         pCur = pParent;
         pParent = pCur->_pParent;
     }
     else
     {
     // 双亲的平衡因子为正负2，违反了AVL树的平衡性，需要对以pParent为根的树进行旋转处理
      f(2 == pParent->_bf)
      {
              // ...
      }
      else
      {
              // ...
       }

  }


  return true;
}

pCur插入后，pParent的平衡因子一定需要调整，在插入之前，pParent的平衡因子分为三种情况：-1，0, 1, 分以下两种情况：

如果pCur插入到pParent的左侧，只需给pParent的平衡因子-1即可
如果pCur插入到pParent的右侧，只需给pParent的平衡因子+1即可

此时：pParent的平衡因子可能有三种情况：0，正负1，正负2

如果pParent的平衡因子为0，说明插入之前pParent的平衡因子为正负1，插入后被调整
成0，此时子树的高度没有变化，所以无需继续往上调整
如果pParent的平衡因子为正负1，说明插入前pParent的平衡因子一定为0，插入后被更
新成正负1，此时该子树的高度增加，所以需要往上继续调整
如果pParent的平衡因子为正负2，则pParent的平衡因子违反平衡树的性质，需要对其进
行旋转处理

AVL树的旋转

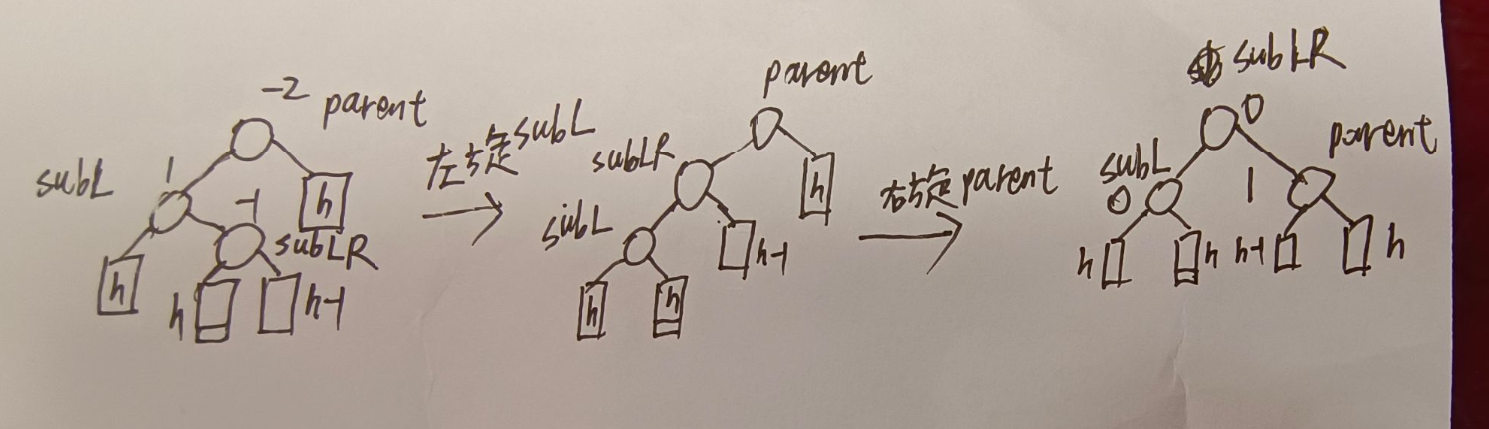
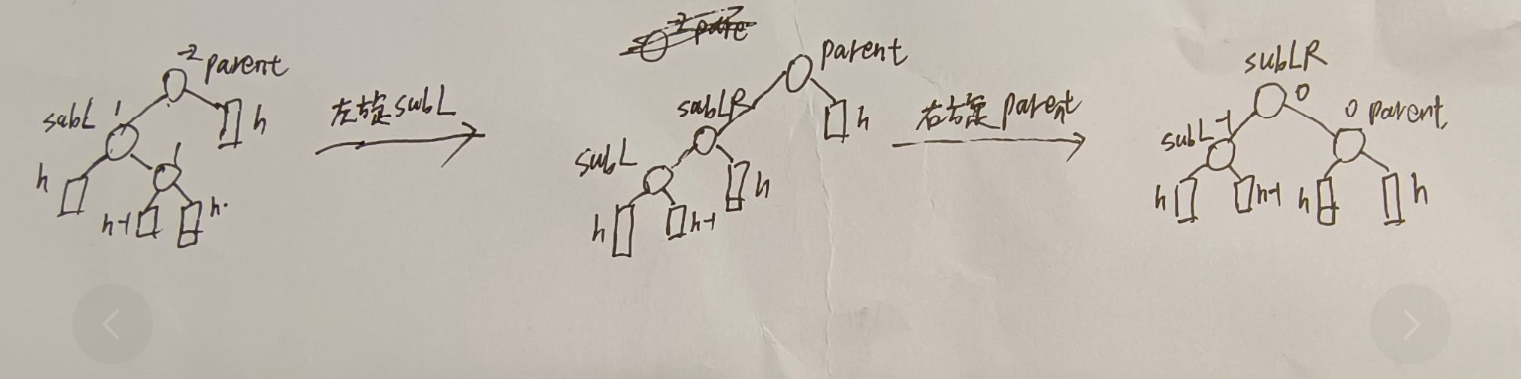
parent平衡因子为-2：

为-2说明parent左边高，那就找到parent左孩子节点subL，假如subL的平衡因子为-1，说明还是左边高，那就一个parent的右旋即可

假如subL的平衡因子为1，那就说明右边高，这里subLR的平衡因子会影响最后parent和subL的平衡因子，却不会影响旋转的方式

注意：

1、所谓双旋，起始就是两次单旋而已

2、假如只需要一次单旋，那么会涉及两个节点的平衡因子的改变，且这两个节点平衡因子最后都会是0

3、假如需要两次旋转，会涉及到三个节点，其中会有两个节点的平衡因子最后是0，另一个节点平衡因子根据subLR或subRL一开始的平衡因子来决定

4、一次单旋中，会涉及到四个节点，其中有两个节点都可能为空（最上面和最下面），最终需要调整的指针个数是4~6，两个不可能为空的节点各有两个指针需要调整，那两个可以为空的节点每有一个不为空，那就会多一个需要调整的指针

parent的平衡因子为2：

仿照为-2的思路即可

AVL树的验证

AVL树是在二叉搜索树的基础上添加了平衡因子的设置，所以AVL树的验证分为两步，一个是二叉搜索树性质的验证，另一个是平衡树性质的验证

1、对搜索树性质的验证看中序是不是有序的

2、对平衡树性质的验证检查每个节点的平衡因子绝对值不超过1即可

AVL树的模拟实现

AVL树模拟

红黑树

红黑树的概念

红黑树是在搜索树的基础上添加了颜色规则，对于一颗红黑树，要么该树是一颗空树，要么该树的根节点是黑，每条路径上都有相同数量的黑色节点，且不能有相邻的红色节点

红黑树不像AVL树一样保证绝对的平衡，而是保证该树的最长路径不会超过最短路径的二倍，保证的是相对的平衡，这样放宽条件可大大减少旋转次数提高效率

为什么最长路径不超过最短路径的二倍？

每条路径上的黑色节点个数相同，不能有相邻的红色节点，所以最长路径就是红色间隔黑色，而最短路径就是只有黑色，所以最长路径是最短路径的二倍

红黑树节点的定义

cpp 复制代码

// 节点的颜色
enum Color{RED, BLACK};
// 红黑树节点的定义
template<class ValueType>
struct RBTreeNode
{
 RBTreeNode(const ValueType& data = ValueType()，Color color = RED)
     : _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr)
     , _data(data), _color(color)
 {}
 RBTreeNode<ValueType>* _pLeft;   // 节点的左孩子
 RBTreeNode<ValueType>* _pRight;  // 节点的右孩子
 RBTreeNode<ValueType>* _pParent; // 节点的双亲(红黑树需要旋转，为了实现简单给
出该字段)
 ValueType _data;            // 节点的值域
 Color _color;               // 节点的颜色
};

**注意：**红黑树节点的默认构造我们给的是红色，因为如果插入黑色节点，那么一定会破坏每条路径有相同数量黑色节点的规则，而如果插入红色节点则不一定破坏

红黑树的插入操作

红黑树是在二叉搜索树的基础上加上颜色条件，因此红黑树的插入可分为两步：

按照二叉搜索树规则插入新节点
新节点插入后，检查红黑树不能有相邻红色节点的性质是否遭到破坏
插入红色新节点cur，如果parent是黑色，那就不用调整
如果parent是红色，那就得调整，因为红黑树的根节点是黑色，所以parent肯定不是根节点，不是根节点那parent的父节点肯定存在，因为不能有相邻红色节点，所以grandfa一定是黑色，这时我们要根据叔叔节点来判断调整策略，我们需要先判断parent是grandfa的哪个孩子，然后就能得到叔叔节点了

1、叔叔节点存在且为红色

只需要将parent和uncle变为黑色，grandfa变为红色，grandfa子树每条路径的黑色节点个数不变，但需要往上继续调整，因为变红的granfa很有可能会再次导致有相邻的红色节点

cur是parent的左孩子还是右孩子不重要，因为调整策略是给parent和uncle变色，根本就没有旋转

2、叔叔节点不存在或叔叔节点存在且为黑色

这时cur是parent的左孩子还是右孩子是有关系的，因为这时必须涉及旋转

假如parent是左孩子，cur也是左孩子，那这时就grandfa右旋，右边的路径黑色节点个数不变，左边的黑色节点个数减1，然后grandfa变色，右边路径的黑色节点个数也减1，然后parent再变成黑色，所有路径黑色节点个数加一，和之前一样，并且此时不再需要往上继续调整了，因为parent是子树的根且是黑色

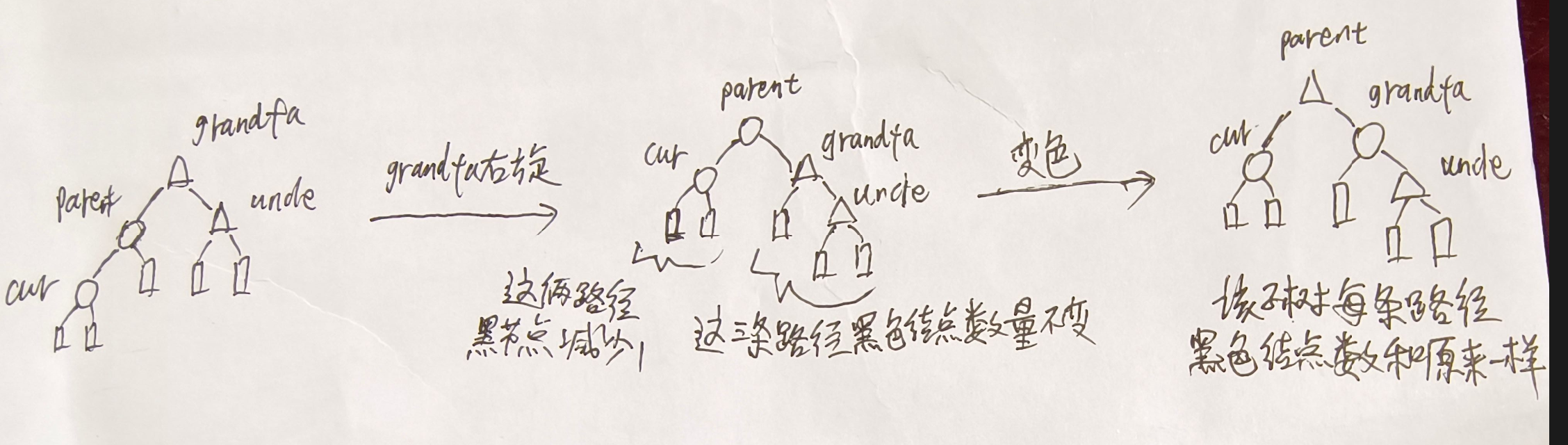
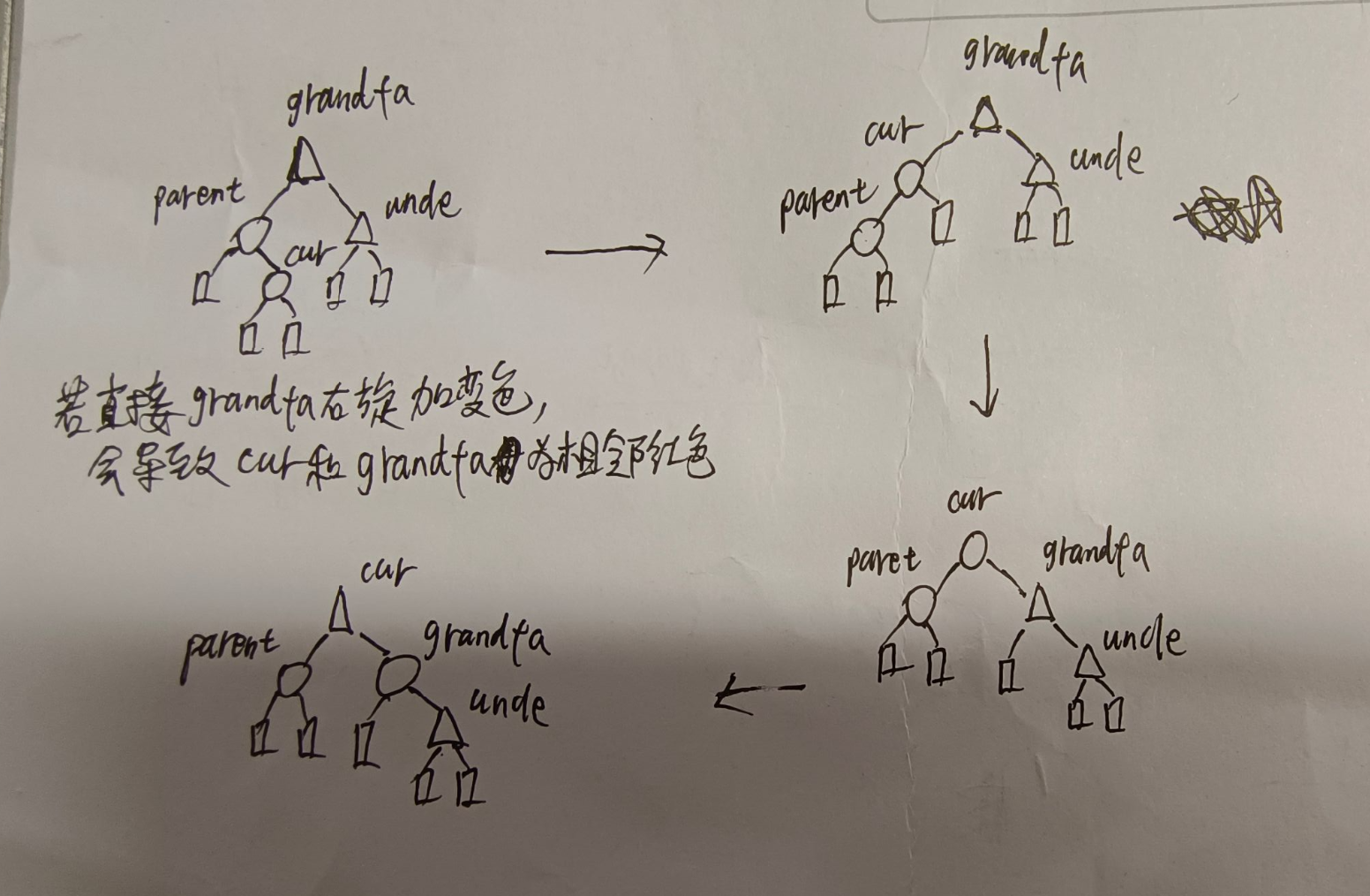
假如parent是左孩子，cur是右孩子，那这时单单一个右旋加变色就不行了，因为最后cur和grandfa都是红色，还是不合规则，所以要进行两次旋转，先对parent左旋，然后对grandfa右旋，最后将grandfa和变成红，cur变成黑

红黑树的验证

红黑树是在二叉搜索树的基础上添加了颜色规则，所以要验证的有四点，中序是否有序来检验是不是搜索树，根节点是否为黑、是否不存在相邻的红色节点、每条路径上黑色节点个数是否相同三点保证是平衡树，如果都满足就是红黑树

红黑树与AVL树的比较

红黑树和AVL树都是高效的平衡二叉搜索树，查询的时间复杂度都是log2n，红黑树不追求绝对平衡，其只保证最长路径不超过最短路径的2倍，相对而言，减少了插入删除导致旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

红黑树的迭代器

begin()与end()

STL明确规定，begin()与end()代表的是一段前闭后开的区间，而对红黑树进行中序遍历后可以得到一个有序的序列，因此，begin()返回的迭代器指向的是红黑树中最小节点(即最左侧节点) ，end()返回的迭代器指向的是最大节点(最右侧节点)的下一个位置，关键是最大节点的下一个位置在哪块？
我们在设计红黑树迭代器的时候，其实结构和链表的迭代器结构差不多，里面有一个红黑树节点的指针，对于最大节点的下一个位置，我们选用的方案是让红黑树节点指针的值为nullptr，然后end()--会使红黑树节点指针指向最大节点，要实现这个操作，我们必须在迭代器中记录红黑树根节点才可以，不然仅凭一个nullptr如何找到最大节点

operator++和operator--

++操作就是让红黑树节点指针指向下一个键更大的节点，如果当前节点右子树不为空，那下一个就是右子树的最小节点，如果为空，左子树都是比该节点小的，所以得往上找该节点的（右向父节点），就是父节点的左子树包含该节点。

--操作就是让红黑树结点指针指向上一个更小的值，如果该节点的左子树不为空，那就应该指向左子树中最大节点，如果左子树为空，那右子树全是比该节点大的，不和条件，所以要往上找左向父节点，也就是父节点右子树包含该节点。
总结：
1、红黑树迭代器中有红黑树节点的指针，其中begin（）返回的迭代器，指向的是最小节点，end()返回的迭代器，指向的是最大节点的下一个位置，也就是nullptr
2、要想完成end()--然后指向最大节点这个操作，光靠一个nullptr肯定不行，所以迭代器中还需要记录红黑树的根节点

红黑树的模拟实现（包含迭代器）

红黑树模拟实现

关联式容器

序列式容器 (Sequence Containers)

关联式容器 (Associative Containers)

键值对

树形结构的关联式容器

set

set的使用

模板参数列表

构造函数

begin

end

empty

size

insert

erase

swap

clear

find

count

set的模拟实现

map

map的使用

模板参数列表

构造函数

begin

end

empty

size

insert

erase

swap

clear

find

count

operator[]

map的模拟实现

multiset

multimap

AVL****树

AVL树的概念

AVL树节点的定义

AVL树的插入

AVL树的旋转

AVL树的验证

AVL树的模拟实现

红黑树

红黑树的概念

红黑树节点的定义

红黑树的插入操作

1、叔叔节点存在且为红色

2、叔叔节点不存在或叔叔节点存在且为黑色

红黑树的验证

红黑树与AVL树的比较

红黑树的迭代器

begin()与end()

operator++和operator--

红黑树的模拟实现（包含迭代器）

AVL树