跳表（SkipList）平衡树的数据结构设计与并发实践

1. 《跳表深度解析：从原理到实战，为什么Redis和LevelDB都选择它？》

2. 《跳表VS红黑树：谁才是并发环境下的王者数据结构？》

3. 《图解跳表：5张图彻底掌握这个O(log n)的优雅数据结构》

4. 《ConcurrentSkipListMap实现原理：Java并发跳表的精妙设计》

5. 《跳表设计哲学：用概率和随机性构建的高性能索引系统》

二、跳表：重新定义快速查找的数据结构

在计算机科学的世界里，我们一直在寻找能够高效存储和检索数据的数据结构。平衡二叉树（如AVL树、红黑树）长期统治着这一领域，直到1989年，William Pugh教授提出了一种革命性的替代方案------跳表（SkipList）。这种数据结构以其惊人的简洁性和媲美平衡树的性能，迅速在各大系统中崭露头角。

2.1 跳表的核心设计思想

跳表的本质是一个多层次的、有序的链表结构。它的设计灵感来自于现实生活中的地铁系统：有快车（特急）和慢车（各站停车）之分。快车只停靠主要车站，可以快速到达较远的目的地；而慢车站站都停，可以从任意站点出发。

 L3: 头  -----------------------> 42 -----------------------> 尾
      ↓                           ↓                           ↓
 L2: 头 --------> 19 --------> 42 --------> 65 --------> 尾
      ↓           ↓           ↓           ↓           ↓
 L1: 头 -> 7 -> 19 -> 26 -> 42 -> 50 -> 65 -> 79 -> 尾
      ↓   ↓   ↓   ↓   ↓   ↓   ↓   ↓   ↓
 L0: 头-7-19-26-42-50-65-79-尾 (底层完整有序链表)

核心特性：

• 底层（L0）：包含所有元素的有序单向链表

• 上层索引层：通过随机算法生成，加速查找过程

• 时间复杂度：查找、插入、删除均为O(log n)（平均情况）

• 空间复杂度：O(n)，比原始链表多约2倍的节点

2.2 跳表的工作原理深度剖析

2.2.1 查找操作：多层搜索的艺术

查找是跳表最核心的操作。算法从最高层开始，利用索引快速跳过大量元素：

 查找元素50的过程：
 1. L3: 头 → 42 (50>42，继续前进) → 尾 (到达末尾，下降一层)
 2. L2: 42 → 65 (50<65，下降一层)
 3. L1: 42 → 50 (找到!)

算法步骤：

1. 从最高层头节点开始

2. 在当前层向右移动，直到下一个节点值大于等于目标值

3. 如果当前节点值等于目标值，返回成功

4. 否则下降一层，重复步骤2-3

5. 到达底层仍未找到，返回失败

这种"先横后纵"的搜索策略，使得跳表能够像二分查找一样快速定位元素。

2.2.2 插入操作：随机确定层数的智慧

插入操作的巧妙之处在于随机确定新节点的层数：

 # 随机层数生成算法（常用实现）
 def random_level():
     level = 1
     # 以1/2的概率增加层数
     while random() < 0.5 and level < MAX_LEVEL:
         level += 1
     return level

插入过程：

1. 通过查找算法找到插入位置的前驱节点（每层记录）

2. 随机生成新节点的层数k

3. 创建新节点，将其插入到0到k层的链表中

4. 更新相关节点的指针

这个随机过程确保了高层索引的稀疏性：大约1/2的节点有第1层索引，1/4有第2层，1/8有第3层...这种分布自然形成了类似平衡树的结构。

2.2.3 删除操作：安全的指针更新

删除操作需要找到待删除节点在每一层的前驱节点，然后安全地更新指针：

1. 查找待删除节点，记录每一层的前驱节点

2. 从最高层到底层，逐层更新前驱节点的next指针

3. 释放被删除节点的内存

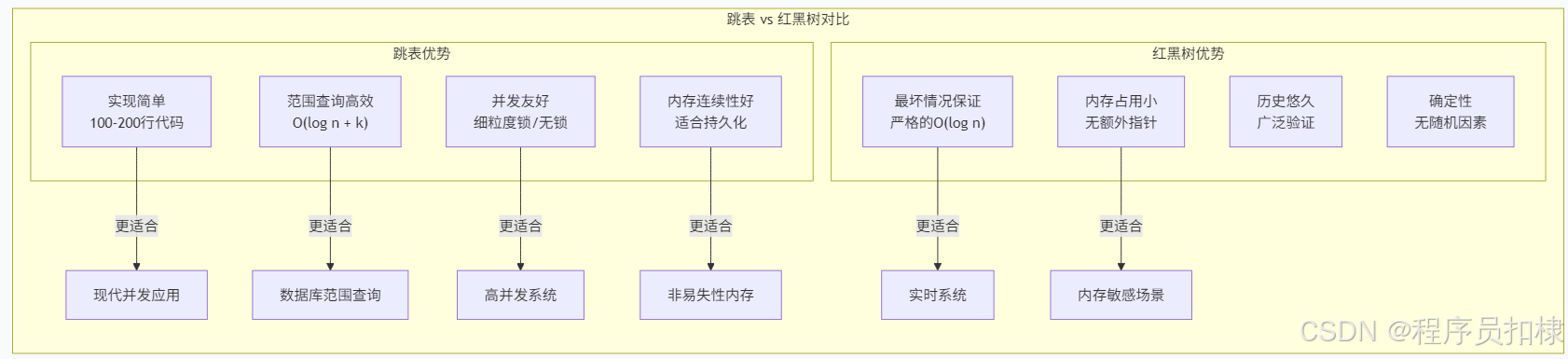
2.3 跳表与平衡树的对比优势

2.3.1 实现简单性

红黑树的实现通常需要300-500行代码，需要考虑多种旋转情况和颜色调整。而跳表的核心实现通常只需100-200行代码，逻辑清晰直观。

2.3.2 范围查询的高效性

跳表进行范围查询(range query)极为高效：

 查询[26, 65]之间的所有元素：
 1. 先查找26（O(log n)）
 2. 从26开始，在底层链表向右遍历直到超过65（O(k)，k为结果数量）

相比之下，平衡树需要进行复杂的中序遍历。

2.3.3 并发友好的设计

这是跳表最显著的优势之一。在并发环境下：

• 平衡树：通常需要全局锁或复杂的锁策略

• 跳表：可以使用细粒度锁或无锁编程

2.4 ConcurrentSkipListMap：Java并发跳表的实现精髓

Java的ConcurrentSkipListMap是跳表在并发环境下的经典实现，其设计哲学体现了现代并发数据结构的智慧。

2.4.1 无锁查找

查找操作完全不需要锁！这是因为：

1. 节点一旦插入，就不会被移动（只更新指针）

2. 使用volatile保证内存可见性

3. 允许"先发布后连接"的弱一致性

2.4.2 乐观锁插入

插入操作采用CAS（Compare-And-Swap）原子操作：

 // 伪代码展示插入的核心思想
 do {
     // 1. 找到插入位置的前驱和后继节点
     // 2. 创建新节点，指向后继
     // 3. CAS更新前驱的next指针
 } while (!casSuccess);

如果CAS失败（其他线程修改了链表），则重试整个查找过程。

2.4.3 标记删除策略

删除操作采用两步法：

1. 逻辑删除：将节点标记为已删除

2. 物理删除：在适当的时候从链表中移除

这种"懒删除"策略避免了复杂的同步问题。

2.5 跳表的实际应用场景

2.5.1 Redis有序集合

Redis的Sorted Set使用跳表作为底层实现之一，支持：

• O(log n)的插入、删除、查找

• 高效的范围查询（ZRANGE命令）

• 排名查询（ZRANK命令）

2.5.2 LevelDB/RocksDB

这些KV存储引擎使用跳表作为内存表（MemTable）的实现：

• 支持快速写入（内存中排序）

• 支持高效的范围扫描

• 易于实现快照和并发控制

2.5.3 Apache Cassandra

Cassandra使用跳表维护SSTable中的索引，充分利用其并发友好的特性。

2.6 跳表的性能优化技巧

2.6.1 层数限制策略

 // 动态调整最大层数
 MAX_LEVEL = Math.max(16, (int)(Math.log(expectedSize) / Math.log(2)));

2.6.2 概率参数调优

调整层数增长概率可以平衡时间和空间：

• 降低概率（如1/4）：减少空间开销，略微增加查找时间

• 提高概率（如3/4）：加快查找速度，增加空间使用

2.6.3 内存布局优化

 // 紧凑型节点结构
 struct SkipListNode {
     int value;
     int level;
     SkipListNode* next[1]; // 柔性数组，根据level动态分配
 };

2.7 跳表的局限性及应对策略

1. 内存开销：比红黑树多约2倍内存

   • 应对：使用压缩指针、对象池等技术

2. 最坏情况性能：理论上可能退化为O(n)

   • 应对：设置合理的最大层数限制

3. 缓存局部性：不如数组结构友好

   • 应对：节点内存预分配、缓存友好布局

2.8 未来展望：跳表在新时代的应用

随着非易失性内存（NVM）和多核处理器的普及，跳表的优势将进一步凸显：

• NVM友好：指针操作比树旋转更适合持久化内存

• 可扩展性：更好的多核并发性能

• 机器学习集成：自适应调整索引策略

三、总结

跳表以其优雅的设计哲学------用简单的随机性替代复杂的确定性规则，在数据结构领域开辟了一条新路。它告诉我们，有时候"足够好"的随机解决方案，比"绝对完美"的确定性方案更具实用价值。

在分布式系统、数据库、实时计算等对并发性能要求极高的领域，跳表正逐渐成为首选的数据结构。它的成功不仅在于技术上的优势，更在于其设计理念的先进性：在简单与高效之间找到了完美的平衡点。

正如计算机科学大师Donald Knuth所言："跳表是那些你希望自己早就发明出来的算法之一。"掌握跳表，不仅意味着掌握了一种高效的数据结构，更意味着理解了一种以简驭繁的工程智慧。

---