关键词:Rejection sampling
文章目录
- 一、说明
- 二、什么是拒收抽样?
-
- [2.1 什么是蒙特卡罗方法?](#2.1 什么是蒙特卡罗方法?)
- [2.2 什么是拒收抽样?](#2.2 什么是拒收抽样?)
- [2.3 简单例子演示拒收抽样是如何运作的?](#2.3 简单例子演示拒收抽样是如何运作的?)
- 三、拒收抽样实例
- [四、一个简单的 Python 实现](#四、一个简单的 Python 实现)
- 五、后记
一、说明
拒绝抽样是一种统计方法,它利用一个包络函数从目标分布中生成样本。该包络函数限定了目标分布的密度范围,并允许基于包含目标密度和包络密度的概率准则来接受样本。该技术从目标分布中生成独立样本,并且需要选择合适的包络函数来最大化接受概率并最小化计算效率损失。
二、什么是拒收抽样?
2.1 什么是蒙特卡罗方法?
如果一种方法/算法使用随机数来解决问题,则它被归类为蒙特卡罗方法。在拒绝抽样中,蒙特卡罗方法(即随机性)有助于在算法中实现某个准则。
2.2 什么是拒收抽样?
拒绝抽样是一种蒙特卡罗算法,它借助代理分布从复杂的("难以抽样的")分布中抽取数据。
就抽样而言,几乎所有蒙特卡罗方法的核心思想是:如果无法从目标分布函数中采样,则使用另一个分布函数(因此称为提议函数)。
然而,抽样程序必须"遵循目标分布"。遵循"目标分布"意味着我们应该根据样本出现的概率获得若干个样本。简而言之,应该从高概率区域抽取更多样本。
这也意味着,当我们使用提议函数时,必须引入必要的修正,以确保我们的抽样过程符合目标分布函数!这种"修正"就以验收标准的形式体现出来。
2.3 简单例子演示拒收抽样是如何运作的?
先看一个最最简单的示例:在下图中,我们想得到黄色部分的抽样样本,用蒙特卡洛算法如何获得?
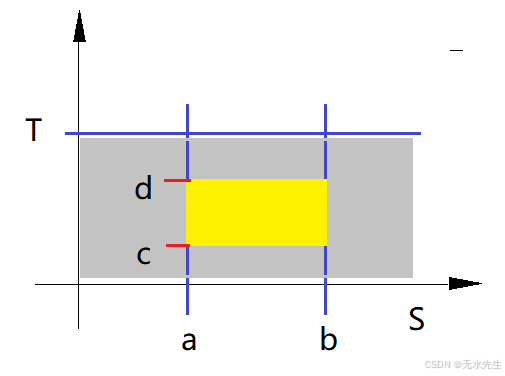
算法如下:
step1:先对横坐标【0,S】区间进行均匀分布抽样,这用计算机获取并不难。
x = u n i s a m p l e ( 0 , S ) x = uni_{sample}(0,S) x=unisample(0,S)
step2:判别x值,如果
i f a < x < b if \;\;\;a<x<b ifa<x<b
保留这个x值.
i f x < a 或 x > b if \;\;\; x<a \;或 \; x>b ifx<a或x>b
放弃这个x值,重新抽取x.
step 3:保留横坐标x,对纵坐标【0,T】区间进行均匀分布抽样,这用计算机获取并不难。
y = u n i s a m p l e ( 0 , T ) y = uni_{sample}(0,T) y=unisample(0,T)
step 4:判别y值,如果
i f c < y < d if \;\;\;c<y<d ifc<y<d
保留这个y值.
i f y < c 或 y > d if \;\;\; y<c \;或 \; y>d ify<c或y>d
放弃这个y值,重新抽取y.
反复上述step1--step4成千上万次,就能得到黄色区域的均匀抽样。这就是拒绝采样的最核心思路。下面我们看一些复杂问题。
三、拒收抽样实例
我将借助一个例子来解释这个算法。考虑一个目标分布函数,我们无法从中进行采样。该函数的图像及其函数形式如下所示。
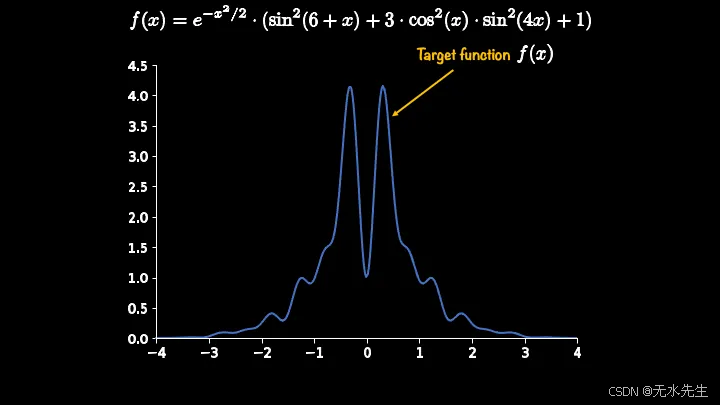
这是一个一维目标函数,我们的任务是获取落在 -3 和 3 之间的样本。提议函数的一种选择是均匀分布函数。下面显示了它的函数形式,即 g(x)。

如果我把这个提议函数和我们的目标函数一起绘制成图表,那么它看起来会像这样:
按回车键或点击查看完整尺寸的图片
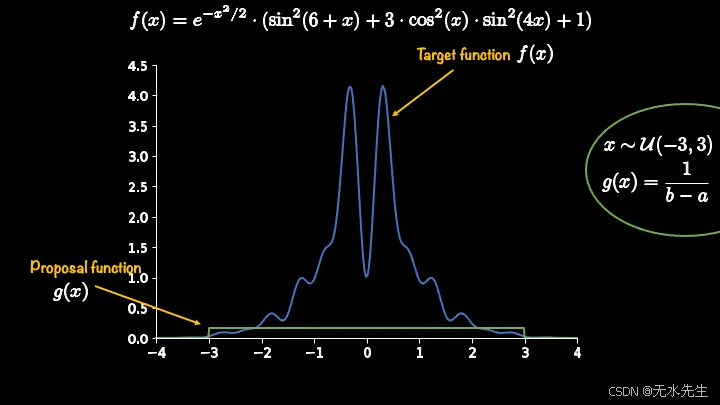
如您所见,目前我们的提案函数并未完全涵盖目标函数。一旦我们制定出修正措施(或验收标准),这种涵盖的重要性就会显现出来。
一个简单的解决方法是对提议函数进行缩放,但缩放常数应该是多少呢?......这是拒绝采样的一个挑战,但对于更简单的一维目标函数,可以通过最大化来获得。这个缩放常数用符号C或M表示。在本教程中,我将使用C。
缩放后,我们的图将如下所示。在本例中, C的值为25。
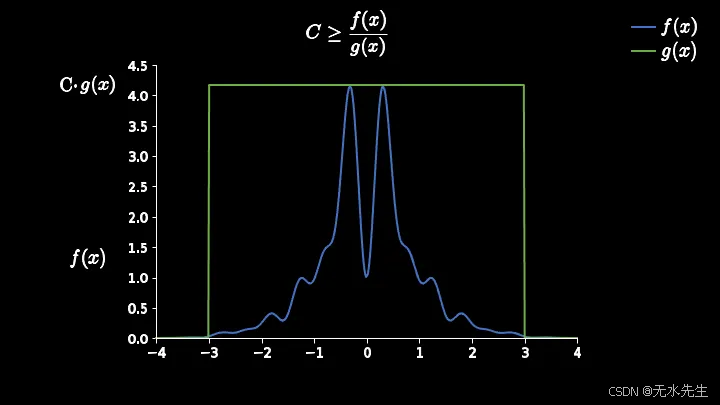
现在我们准备使用提出的函数进行采样。接下来,我们将对这两个函数进行采样结果的评估。为了方便您理解,我在这里用图片来展示。
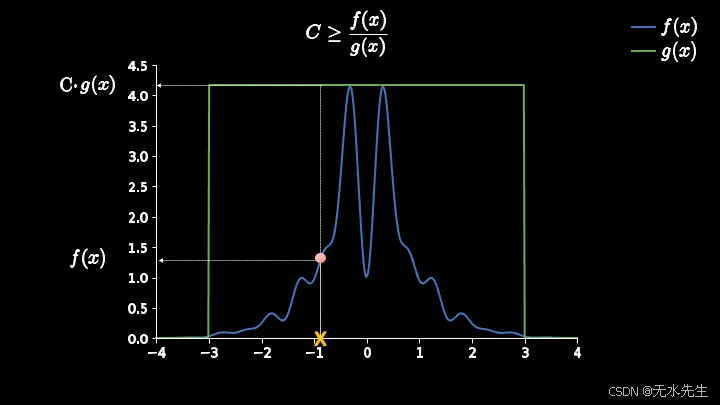
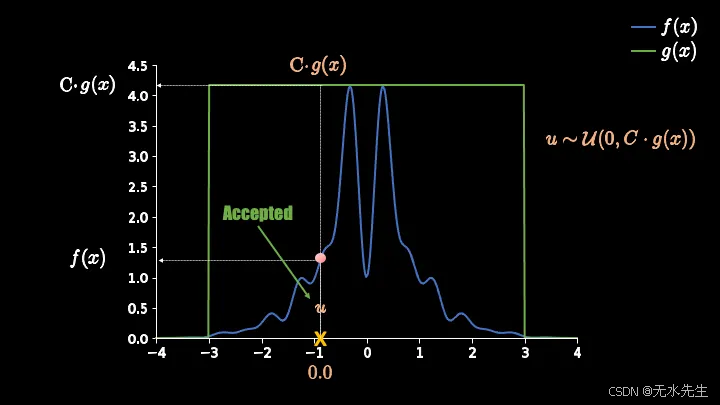
样本用橙色 X 标记。粉色点表示其 f(x) 的值。您还可以看到它在提议函数 g(x) 下的值。由于我们使用均匀分布作为提议函数,因此所有样本出现的概率均相等,它们的值都将等于C g(x)。
现在我们需要找到一个准则,以确保最终结果符合目标分布函数。上面的图应该有助于我们对这个准则形成初步的理解。我将图中粉色点和橙色 X 所在的那条垂直线称为评估线。
你应该这样想------"如果我能在这个评估线上得到一个数字,并且如果这个数字低于粉红色点,那么我就接受样品 X,否则我就拒绝它"。
但是,这个所谓的数字从何而来?我们如何确保它会落在所谓的评估线上?
这就需要用到随机性(也就是蒙特卡罗方法)。但在此之前,让我先展示一下这个图的旋转版本,它能提供更好的可视化效果(希望也能帮助你更好地理解)。
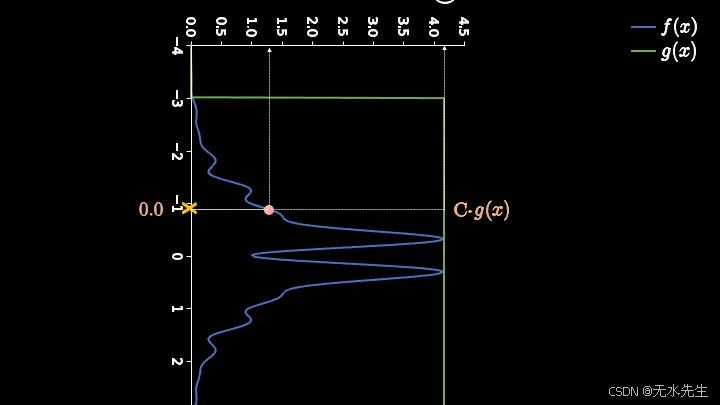
在这个旋转后的版本中,我们可以看到坐标轴的范围是 (0, Cg(x)),接受样本 X 的标准是找到一个介于 0 和 Cg(x) 之间的数字。如果这个数字位于粉色点的左侧,我们就接受样本;否则,我们就拒绝样本。
这里的核心思想是,粉色标记左右两侧的线段并不相等,并且(在某种程度上)反映了样本出现的概率。但问题仍然是,谁来告诉我们这个落在评估线上的数值呢?
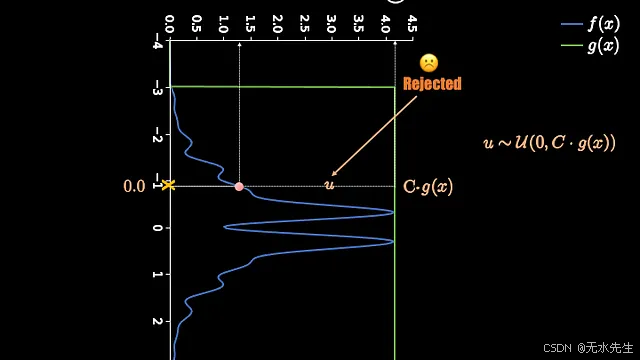
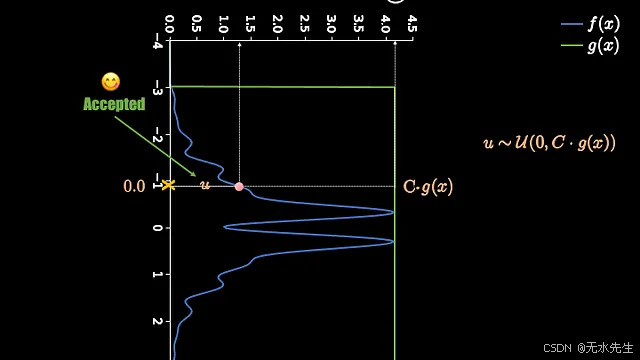
为了得到这个数值,我们将使用另一个取值范围为 0 到 Cg(x) 的均匀分布。尽管均匀分布中的所有随机数出现的概率均等,但我们可以看到,由于评估线的宽度更大,落在右侧的数值也会更多。正是这种随机性的运用,使得该算法被归类为蒙特卡罗算法。以下两张图分别展示了接受和拒绝事件。
根据以上解释,可以看出我们对 X 的接受标准可以用数学方式表示为:

也就是说,如果"u"低于粉色点,我们就接受!......请参见下图的原始图表:
需要注意的是,当样品被拒收时,我们会将其丢弃并重复该过程,即
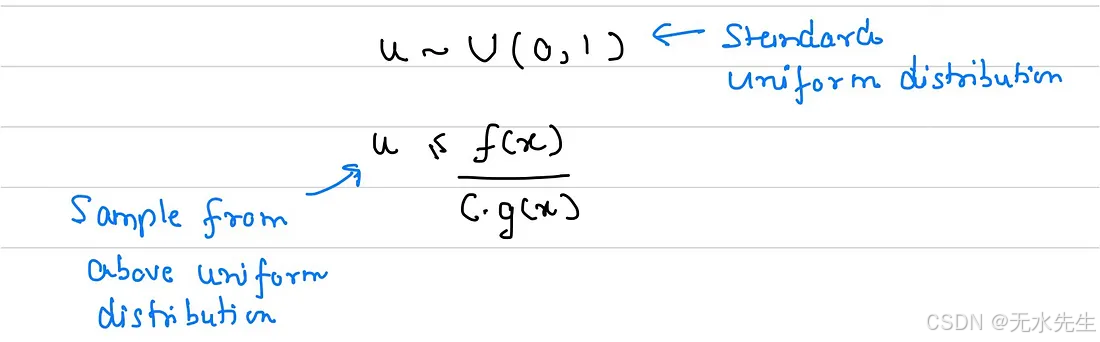
我还想让你们熟悉一下该验收准则的另一种表述方式。在这种表述方式中,我们将从均匀分布中获取"u",该均匀分布的样本值介于 0 到 1 之间,即标准均匀分布。如果使用这种表述方式,则验收准则如下所示:
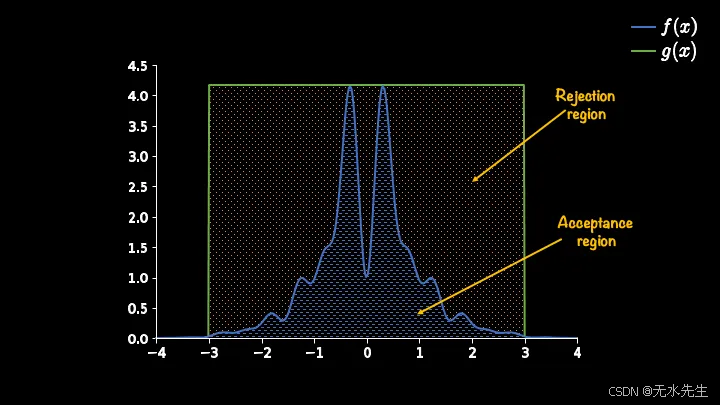
如果我们多次重复此算法,最终会得到如下所示的图表:
显而易见,很多样品都会被拒收😩
一种解决方法是通过选择另一个提议分布函数来缩小拒绝域。请记住,您应该选择既能进行有效采样又能很好地概括目标函数(当然,是在缩放之后!)的提议分布函数。下面我将向您展示如何使用高斯分布作为提议函数。
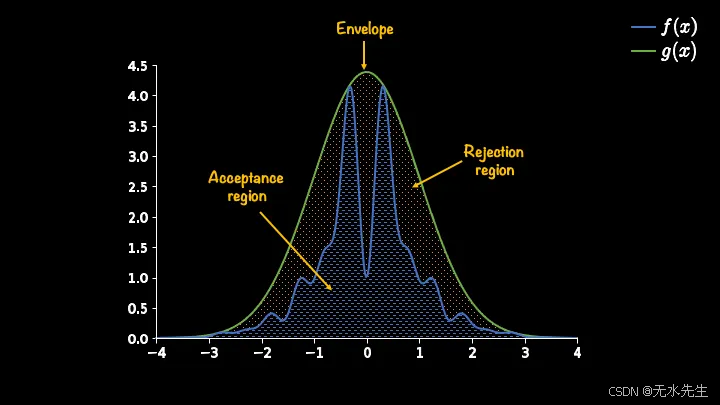
拒绝域已显著缩小。此时,缩放常数 C 为 11。
四、一个简单的 Python 实现

使用上述简单的 Python 实现,我尝试了我们的两种提议分布函数(即均匀分布和高斯分布),结果如下:
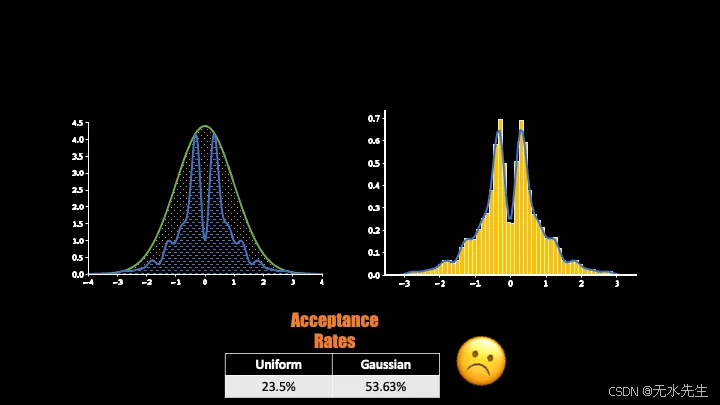
正如预期的那样,选择高斯分布作为提议函数要好得多(接受率为 53.63%),但效率仍然很低!
五、后记
以上我们介绍了最简单的拒收抽样模型。该算法有局限性和挑战,比如效率不高,复杂问题难以实施,不过有很多改进措施,我们将在以后慢慢探讨。