[hot100 NO.13~18]

🔥普通数组

13🎈.最大子数组和

一、核心思路：动态规划（DP）

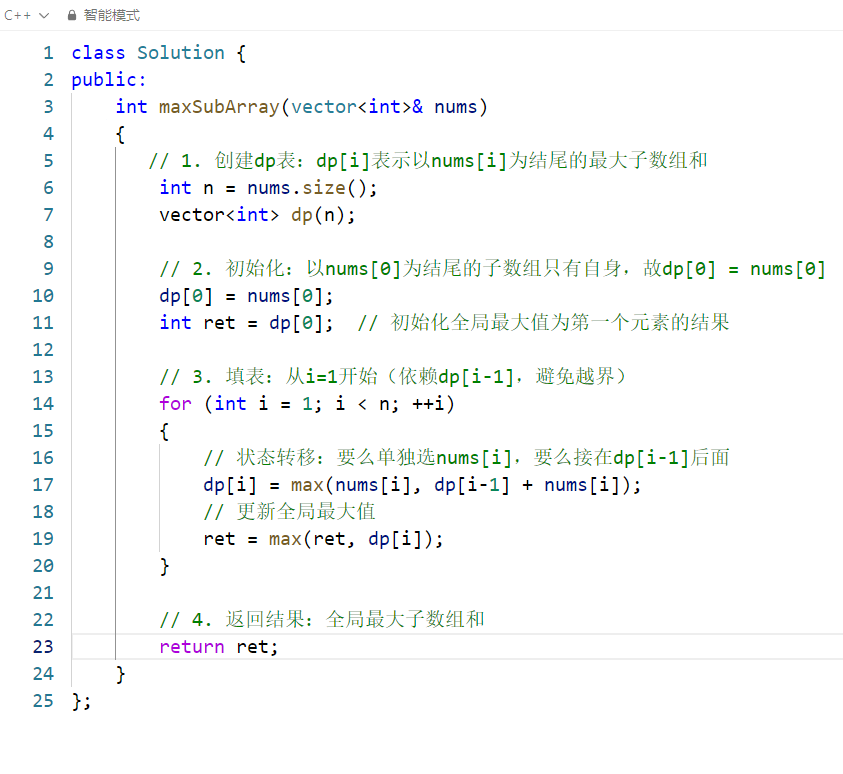
该解法的核心是动态规划 ，通过定义状态 dp[i] 表示「以 nums[i] 为结尾的最大子数组和」，将原问题拆解为更小的子问题，逐步推导最优解。

二、代码逐行解析

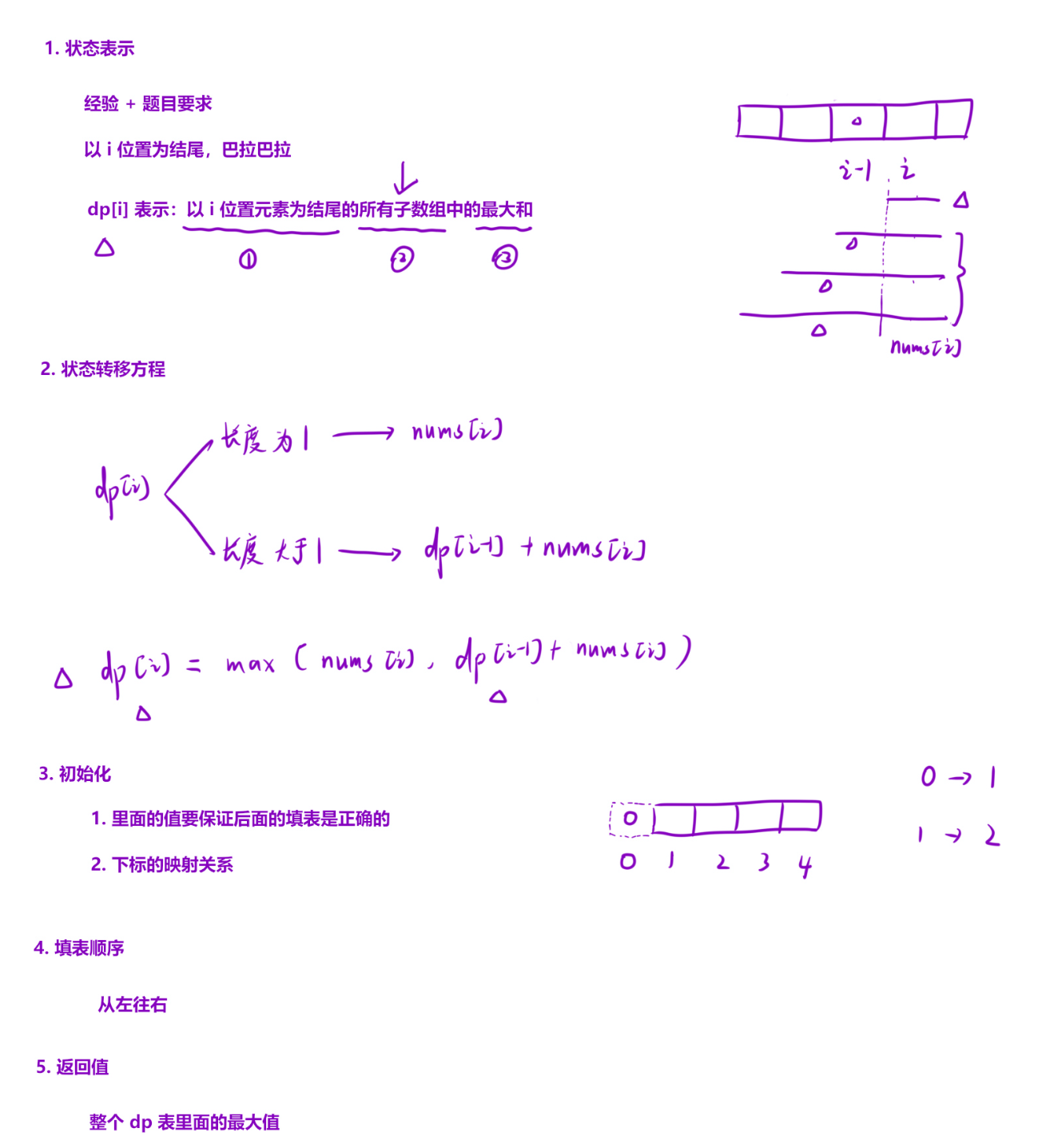
1. 状态定义

cpp 复制代码

// 1. 创建dp表：dp[i]表示以nums[i]为结尾的最大子数组和
int n = nums.size();
vector<int> dp(n);

dp[i] 的含义：必须包含 nums[i] 的子数组中，能得到的最大和。（例如：nums = [-2,1,-3]，则 dp[1] = 1（子数组 [1]），dp[2] = max(-3, 1+(-3)) = -2（子数组 [-3]））
为什么要「以 nums[i] 结尾」？保证状态转移的连续性：dp[i] 仅依赖前一个状态 dp[i-1]，避免遗漏子数组的衔接情况。

2. 初始化

cpp 复制代码

// 2. 初始化：以nums[0]为结尾的子数组只有自身，故dp[0] = nums[0]
dp[0] = nums[0];
int ret = dp[0];  // 初始化全局最大值为第一个元素的结果

边界条件：数组第一个元素没有前驱，因此以 nums[0] 结尾的子数组只能是它自己，故 dp[0] = nums[0]。
ret 用于记录全局最大子数组和 （因为最终答案不一定是 dp[n-1]，例如 nums = [1,-2,3]，dp[2]=3 才是最大值）。

3. 状态转移（填表）

cpp 复制代码

// 3. 填表：从i=1开始（依赖dp[i-1]，避免越界）
for (int i = 1; i < n; ++i) 
{
    // 状态转移：要么单独选nums[i]，要么接在dp[i-1]后面
    dp[i] = max(nums[i], dp[i-1] + nums[i]);
    // 更新全局最大值
    ret = max(ret, dp[i]);
}

状态转移方程 ：dp[i] = max(nums[i], dp[i-1] + nums[i])对 nums[i] 有两种选择：
- 选择 1：单独作为子数组（放弃前面的子数组），和为 nums[i]；
- 选择 2：接在以 nums[i-1] 结尾的最优子数组后面，和为 dp[i-1] + nums[i]；取两者的最大值，即为「以 nums[i] 结尾的最大子数组和」。
更新全局最大值 ：每次计算完 dp[i]，都要和当前 ret 比较，确保 ret 始终是所有 dp[0...i] 中的最大值。

4. 返回结果

cpp 复制代码

// 4. 返回结果：全局最大子数组和
return ret;

最终 ret 就是整个数组的最大子数组和（不一定以最后一个元素结尾）。

三、示例推演

以 nums = [-2,1,-3,4,-1,2,1,-5,4] 为例：

i	nums[i]	dp[i] = max(nums[i], dp[i-1]+nums[i])	ret（全局最大值）
0	-2	-2	-2
1	1	max(1, -2+1)=1	1
2	-3	max(-3, 1-3)=-2	1
3	4	max(4, -2+4)=4	4
4	-1	max(-1, 4-1)=3	4
5	2	max(2, 3+2)=5	5
6	1	max(1, 5+1)=6	6
7	-5	max(-5, 6-5)=1	6
8	4	max(4, 1+4)=5	6

最终结果为 6（对应子数组 [4,-1,2,1]），符合预期。

四、复杂度分析

时间复杂度：O (n)，仅遍历数组一次，每个元素的计算是 O (1)。
空间复杂度：O (n)，使用了长度为 n 的 dp 数组（可优化为 O (1)：仅用变量保存前一个 dp 值，无需数组）。

五、空间优化版（可选）

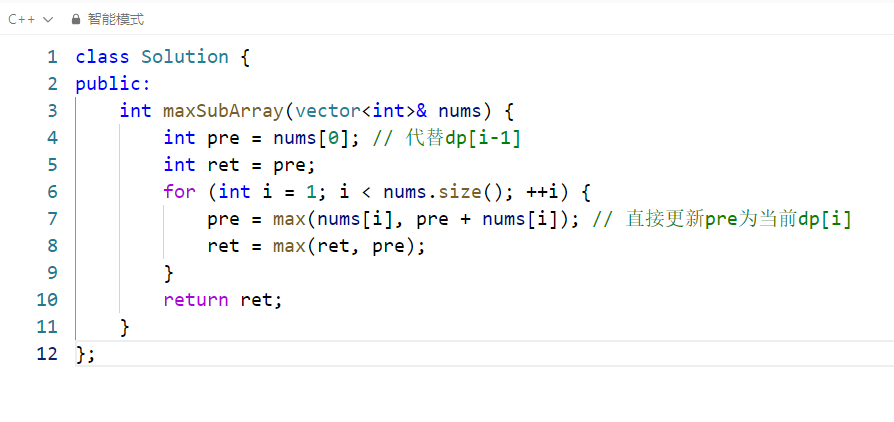
去掉 dp 数组，用 pre 变量保存前一个状态，空间复杂度降至 O (1)，逻辑完全等价。

总结

该解法的核心是动态规划的状态定义技巧：通过「强制以当前元素结尾」的状态定义，将子问题解耦，保证状态转移的简洁性；最终通过全局遍历找到所有可能的子数组和的最大值。

14🎈. 合并区间

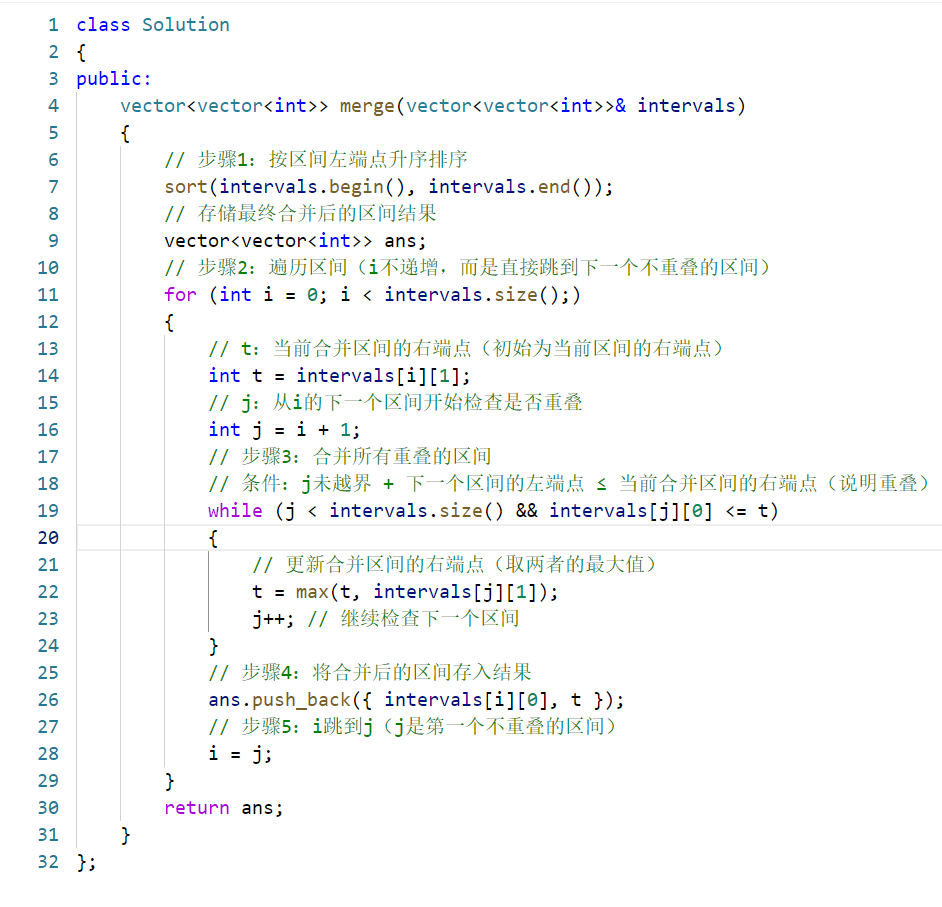
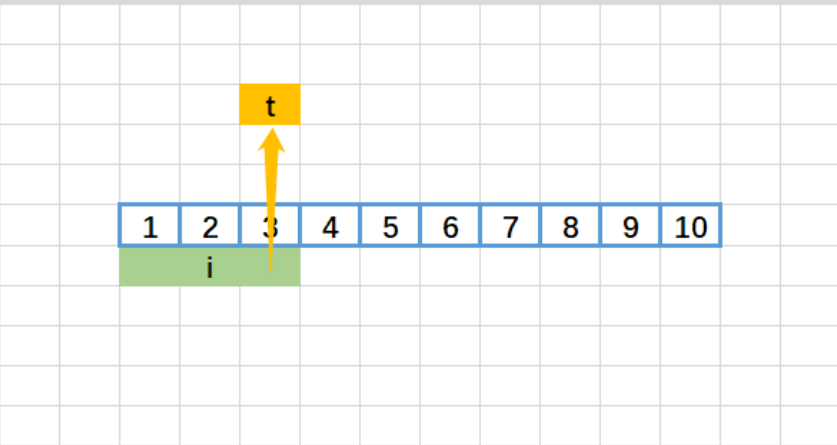
【算法解析：区间合并】

这道题的核心是合并重叠或相邻的区间，代码通过「排序 + 一次遍历合并」的思路实现，时间复杂度主要由排序决定（O (n log n)），空间复杂度 O (log n)（排序的系统栈空间）或 O (n)（存储结果）。

一、核心思路

排序：先按区间的左端点升序排序，确保所有可能重叠的区间都相邻，这是合并的前提；
遍历合并：逐个检查区间，将当前区间与后续所有重叠的区间合并为一个大区间，直到遇到不重叠的区间为止，再将合并后的区间存入结果。

二、关键细节说明

排序规则 ：sort(intervals.begin(), intervals.end()) 对二维向量排序时，默认按第一个元素升序 ，第一个元素相等则按第二个元素升序。例如：输入 [[1,3],[2,6],[8,10],[15,18]] 排序后仍为原顺序；输入 [[2,3],[1,4]] 排序后变为 [[1,4],[2,3]]。
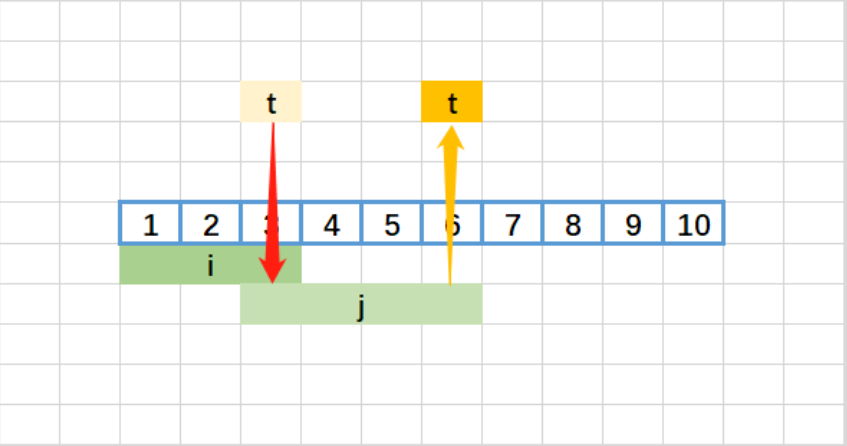
重叠判断条件 ：intervals[j][0] <= t：下一个区间的左端点 ≤ 当前合并区间的右端点 → 两个区间重叠 / 相邻，需要合并。例如：当前合并区间是 [1,3]，下一个区间是 [2,6] → 2 ≤ 3，合并为 [1,6]；若下一个区间是 [4,5] → 4 > 3，不重叠，停止合并。
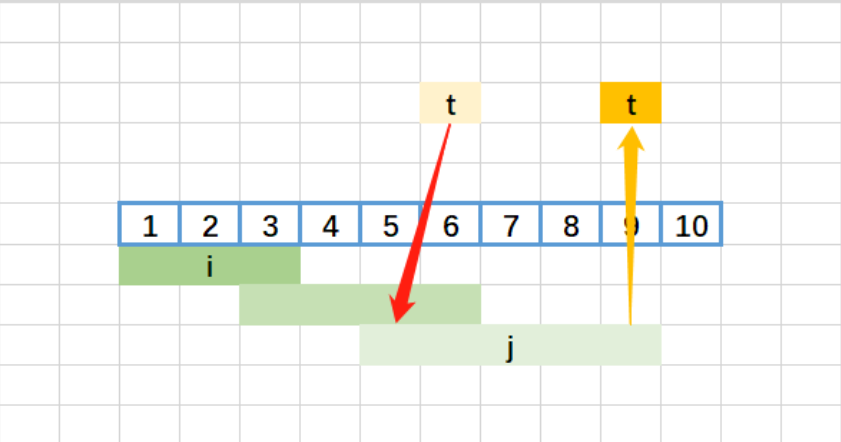
合并区间的右端点更新 ：t = max(t, intervals[j][1])：必须取最大值，避免出现「当前区间包含后续区间」的情况。例如：当前合并区间是 [1,5]，下一个区间是 [2,4] → 合并后右端点仍为 5（而非 4）。
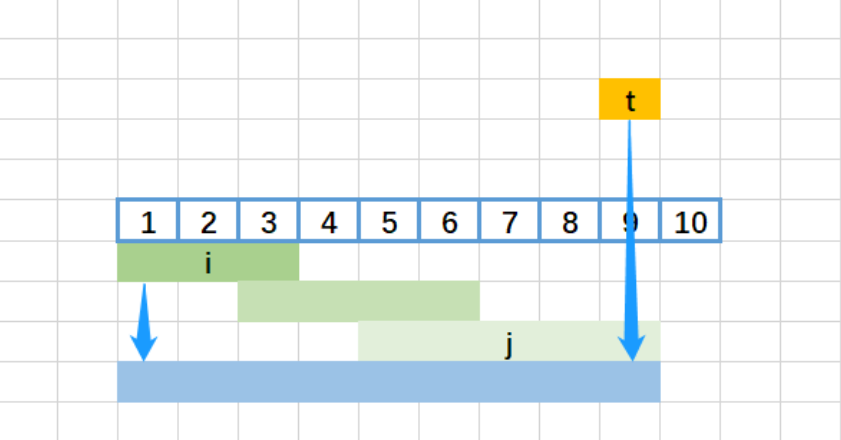
循环变量 i 的更新 ：i = j 而非 i++，因为 j 已经跳过了所有与当前区间重叠的区间，直接跳到下一个需要处理的区间，避免重复遍历。

三、示例演示

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]

排序后：[[1,3],[2,6],[8,10],[15,18]]；
第一次循环（i=0）：
- t = 3，j=1；
- 检查 j=1：2 ≤ 3 → t = max(3,6)=6，j=2；
- 检查 j=2：8 > 6 → 退出 while；
- 存入 [1,6]，i=2；
第二次循环（i=2）：
- t=10，j=3；
- 检查 j=3：15 > 10 → 退出 while；
- 存入 [8,10]，i=3；
第三次循环（i=3）：
- t=18，j=4（越界）→ 退出 while；
- 存入 [15,18]，i=4（循环结束）；
最终结果：[[1,6],[8,10],[15,18]]。

四、边界情况处理

空输入：intervals = [] → 直接返回空数组；
单个区间：intervals = [[1,2]] → 直接返回原区间；
完全重叠：intervals = [[1,10],[2,3],[4,5]] → 合并为 [[1,10]]；
相邻区间：intervals = [[1,2],[3,4]] → 不合并，返回原区间（因为 3 > 2）；若输入是 [[1,2],[2,4]] → 合并为 [[1,4]]（因为 2 ≤ 2）。

总结

该算法的核心是「排序后贪心合并」：排序保证了重叠区间相邻，贪心策略（尽可能合并所有重叠区间）保证了一次遍历即可完成合并，时间效率和空间效率均为最优。

15🎈. 轮转数组

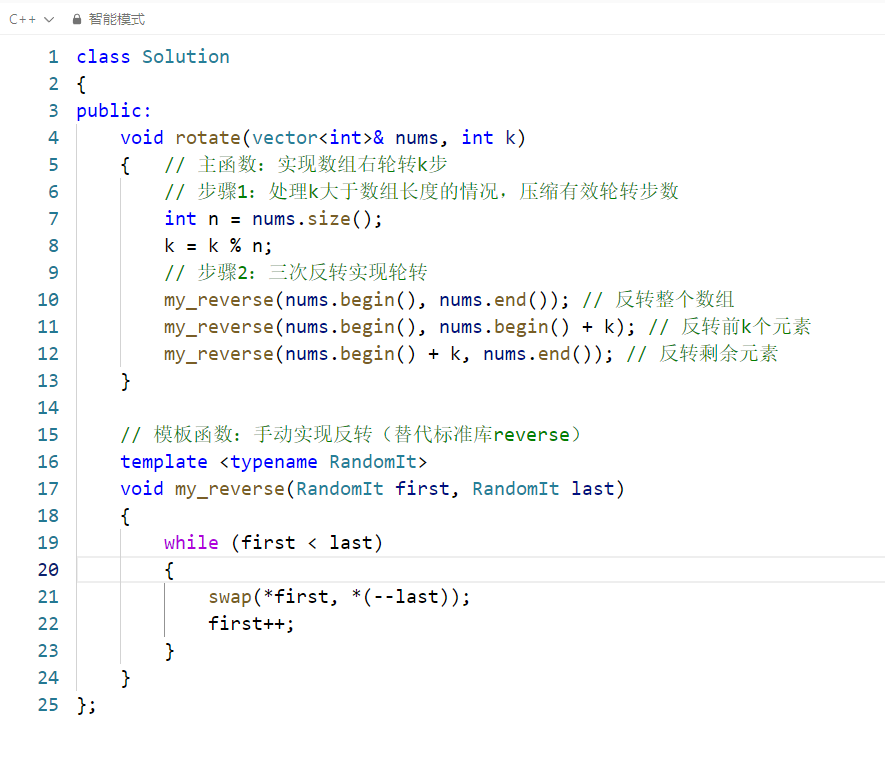
完整代码逐行解析

这份代码的核心是三次反转法实现数组右轮转 ，并手动实现了通用的 my_reverse 反转函数。以下从「代码结构」「核心函数 my_reverse」「轮转逻辑」三个维度拆解，结合示例讲清每一步的作用。

核心函数：`my_reverse` 解析

my_reverse 是手动实现的「通用反转函数」，功能和 C++ 标准库 reverse 完全一致，核心是双指针 + 左闭右开区间。

1. 模板参数 `RandomIt`

含义：「随机访问迭代器」（如 vector<int>::iterator），支持 ++/--/*/< 等操作，保证 O (1) 访问元素；
作用：让函数适配任意可随机访问的容器（vector、array、string 等），而非仅针对 vector<int>。

2. 函数参数 `first` / `last`

first：反转区间的起始迭代器（包含，左边界）；
last：反转区间的结束迭代器（不包含，右边界）；
例：my_reverse(nums.begin(), nums.end()) 表示反转 [0, n) 区间（整个数组）；my_reverse(nums.begin(), nums.begin()+3) 表示反转 [0, 3) 区间（前 3 个元素）。

3. 核心循环逻辑

cpp 复制代码

while (first < last) { // 两指针未相遇时循环
    swap(*first, *(--last)); // 交换元素 + 右指针左移
    first++; // 左指针右移
}

分步拆解 （以反转 [1,2,3,4] 为例，first 指向 1，last 指向 4 的下一位）：

循环次数	first 指向	last 指向	操作	数组变化
初始	1	4 的下一位	--last → last 指向 4	[1,2,3,4]
第 1 次	1	4	swap(1,4) → first++	[4,2,3,1]
第 2 次	2	1	first < last？2 < 1 → 循环结束	最终 [4,3,2,1]

关键细节：

--last：先将 last 左移一位（指向区间最后一个有效元素），再交换，符合「左闭右开」的规则；
swap(*first, *(--last))：*first 取迭代器指向的元素值，swap 交换两个元素的内容；
循环终止条件 first < last：避免中间元素（如数组长度为奇数时的中心元素）重复交换。

三、轮转核心逻辑：三次反转

1. 预处理：`k = k % n`

原因：轮转 n 步等价于不轮转（数组回到原位），因此只需计算 k 对 n 的余数，压缩有效步数；
例：n=7，k=10 → 10%7=3，轮转 10 步和轮转 3 步效果完全一致，减少无效操作。

2. 三次反转的原理（以示例 `nums=[1,2,3,4,5,6,7], k=3` 为例）

步骤	操作	数组变化
初始数组	-	[1,2,3,4,5,6,7]
步骤 1：反转整个数组	my_reverse(0,7)	[7,6,5,4,3,2,1]
步骤 2：反转前 k 个	my_reverse(0,3)	[5,6,7,4,3,2,1]
步骤 3：反转剩余元素	my_reverse(3,7)	[5,6,7,1,2,3,4]（最终）

逻辑本质：

右轮转 k 步 = 「将数组后 k 个元素移到开头」；
三次反转通过「整体反转 + 局部反转」，无需额外空间实现元素迁移：
1. 整体反转：把后 k 个元素翻到 "前 k 个位置"（但顺序是反的）；
2. 反转前 k 个：修正后 k 个元素的顺序；
3. 反转剩余元素：修正前 n-k 个元素的顺序。

3. 三次反转的代码对应

步骤 1：my_reverse(nums.begin(), nums.end()) → 反转整个数组（区间 [0, n)）；
步骤 2：my_reverse(nums.begin(), nums.begin()+k) → 反转前 k 个元素（区间 [0, k)）；
步骤 3：my_reverse(nums.begin()+k, nums.end()) → 反转从 k 到末尾的元素（区间 [k, n)）。

四、时间 / 空间复杂度

时间复杂度 ：O(n)
- my_reverse 反转区间长度为 m 时，时间复杂度 O (m)；
- 三次反转的总长度：n + k + (n-k) = 2n → 整体 O (n)。
空间复杂度 ：O(1)
- 仅使用常数级临时变量（迭代器、交换用的临时值），无额外数组 / 容器，原地修改。

五、边界情况测试

1. k=0（无需轮转）

k%n=0，三次反转依次为：反转整个数组→反转前 0 个（无操作）→反转剩余 n 个（即再次反转整个数组）→ 数组回到原位。

2. n=1（单元素数组）

无论 k 是多少，k%1=0，三次反转后数组不变。

3. k=n（轮转 n 步）

等价于 k=0，数组不变。

4. 示例 2：nums=[-1,-100,3,99], k=2

n=4，k%4=2；
步骤 1：反转整个数组 → [99,3,-100,-1]；
步骤 2：反转前 2 个 → [3,99,-100,-1]；
步骤 3：反转后 2 个 → [3,99,-1,-100]（符合预期）。

六、关键易错点提醒

左闭右开区间 ：my_reverse 的 last 是 "结束的下一位"，比如反转前 3 个元素，需传 nums.begin()+3 而非 nums.begin()+2；
k 取模 ：必须先执行 k = k % n，否则当 k > n 时会导致反转区间越界；
迭代器操作 ：--last 要放在 swap 里，避免先移动 first 导致指针错位。

总结

这份代码的核心是「三次反转法」的高效实现：

手动实现的 my_reverse 保证了通用型和原地操作；
k%n 压缩有效步数，避免无效轮转；
三次反转通过 "整体 + 局部" 的反转逻辑，在 O (n) 时间、O (1) 空间内完成数组右轮转，是该题的最优解法。

16🎈. 除自身以外数组的乘积

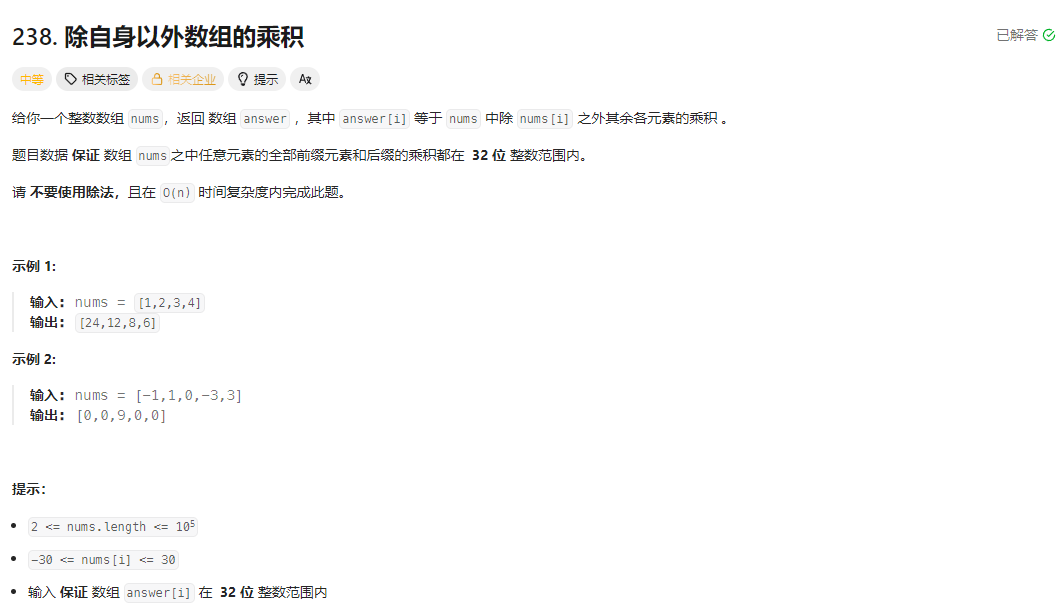
题目背景

要解决的问题是：给定一个整数数组 nums，返回一个数组 ret，其中 ret[i] 等于 nums 中除 nums[i] 之外其余所有元素的乘积。要求不能使用除法，且时间复杂度尽可能优化（最优为 O (n)）。

核心思路

本题的核心是前缀乘积 + 后缀乘积：

前缀乘积数组 f：f[i] 表示 nums[0] 到 nums[i-1] 的乘积（即 i 左侧所有元素的乘积）。
后缀乘积数组 g：g[i] 表示 nums[i+1] 到 nums[n-1] 的乘积（即 i 右侧所有元素的乘积）。
最终结果 ret[i] = f[i] * g[i]（左侧乘积 × 右侧乘积，即排除 nums[i] 的所有元素乘积）。

代码逐行解析

1. 初始化变量

cpp 复制代码

int n = nums.size();
vector<int> f(n), g(n);

n：数组 nums 的长度，后续遍历、数组初始化都依赖这个长度。
f 和 g：分别存储前缀乘积、后缀乘积，长度与 nums 一致。

2. 前缀 / 后缀乘积的边界初始化

cpp 复制代码

f[0] = g[n-1] = 1;

f[0] = 1：第 0 个元素左侧没有元素 ，乘积的 "空集" 定义为 1（乘法单位元），这样后续计算 f[1] = f[0] * nums[0] 才正确。
g[n-1] = 1：最后一个元素右侧没有元素，同理，空集乘积为 1。

3. 计算前缀乘积数组 `f`

cpp 复制代码

for(int i = 1; i < n; i++) {
    f[i] = f[i-1] * nums[i-1];
}

遍历从 i=1 开始（因为 f[0] 已初始化）。
f[i] 的含义：nums[0] ~ nums[i-1] 的乘积（i 左侧所有元素的乘积）。
举例：
- 若 nums = [1,2,3,4]，则：
  - f[1] = f[0] * nums[0] = 1 * 1 = 1（元素 2 左侧只有 1）；
  - f[2] = f[1] * nums[1] = 1 * 2 = 2（元素 3 左侧是 1×2）；
  - f[3] = f[2] * nums[2] = 2 * 3 = 6（元素 4 左侧是 1×2×3）。

4. 计算后缀乘积数组 `g`

cpp 复制代码

for(int i = n-2; i >= 0; i--) {
    g[i] = g[i+1] * nums[i+1];
}

遍历从 i=n-2 开始（因为 g[n-1] 已初始化），从后往前算。
g[i] 的含义：nums[i+1] ~ nums[n-1] 的乘积（i 右侧所有元素的乘积）。
举例（仍以 nums = [1,2,3,4] 为例）：
- g[2] = g[3] * nums[3] = 1 * 4 = 4（元素 3 右侧只有 4）；
- g[1] = g[2] * nums[2] = 4 * 3 = 12（元素 2 右侧是 3×4）；
- g[0] = g[1] * nums[1] = 12 * 2 = 24（元素 1 右侧是 2×3×4）。

5. 计算最终结果

cpp 复制代码

vector<int> ret(n);
for(int i = 0; i < n; i++) {
    ret[i] = f[i] * g[i];
}
return ret;

每个位置 i 的结果 = 左侧乘积 × 右侧乘积。
举例（nums = [1,2,3,4]）：
- ret[0] = f[0] * g[0] = 1 * 24 = 24（排除 1，乘积是 2×3×4）；
- ret[1] = f[1] * g[1] = 1 * 12 = 12（排除 2，乘积是 1×3×4）；
- ret[2] = f[2] * g[2] = 2 * 4 = 8（排除 3，乘积是 1×2×4）；
- ret[3] = f[3] * g[3] = 6 * 1 = 6（排除 4，乘积是 1×2×3）。

复杂度分析

时间复杂度：O (n)。三次遍历数组（前缀、后缀、结果计算），每次遍历都是 O (n)，总时间为 O (n)。
空间复杂度 ：O (n)。额外使用了两个长度为 n 的数组 f 和 g。

17🎈. 缺失的第一个正数

问题分析

要找到未排序整数数组中缺失的最小正整数，且要求时间复杂度 O (n)、空间复杂度 O (1)，核心思路是利用数组本身作为哈希表：

缺失的最小正整数一定在 [1, n+1] 范围内（n 为数组长度），因为如果 [1,n] 都出现，答案就是 n+1。
遍历数组，将数值为 x（且 1≤x≤n）的元素放到数组第 x-1 位（即数值和索引对应）。
再次遍历数组，第一个索引 i 对应的数值不等于 i+1 时，i+1 就是答案；若全部对应，答案为 n+1。

代码解释

归位过程 ：
- 遍历每个元素，若元素 nums[i] 是 [1,n] 范围内的数，且它不在正确的位置（nums[nums[i]-1] != nums[i]），则交换它到正确位置。
- 使用 while 而非 if 是因为交换后当前位置可能又出现新的需要归位的数（例如交换后 nums[i] 仍在 [1,n] 但未归位）。
查找缺失值 ：
- 遍历归位后的数组，第一个 nums[i] != i+1 的位置，i+1 就是缺失的最小正整数。
- 若所有位置都归位（即 [1,n] 都存在），则返回 n+1。

复杂度分析

时间复杂度：O (n)。每个元素最多被交换到正确位置一次，总交换次数为 O (n)，遍历数组也是 O (n)，整体为 O (n)。
空间复杂度：O (1)。仅使用常数级额外空间（交换操作是原地的）。

要理解nums[nums[i] - 1] != nums[i]这个条件，我们需要先回到核心思路 ：把数值 x（满足 1≤x≤n）放到数组中索引为 x-1 的位置（即「数值和索引一一对应」）。

先拆解符号含义

为了方便，我们先定义：

x = nums[i]：当前遍历到的数组第 i 位的数值；
target_idx = x - 1：数值 x 应该在的「正确索引位置」（比如 x=3 应该在索引 2 处，x=1 应该在索引 0 处）；
nums[target_idx]：当前「正确索引位置」上的数值。

因此，nums[nums[i] - 1] != nums[i] 翻译过来就是：当前数值 x 应该在的位置上，放的不是 x 本身 → 说明 x 还没归位，需要交换。

为什么需要这个条件？（反过来看更易理解）

如果去掉这个条件，直接交换 nums[i] 和 nums[x-1]，会出现无限循环的问题。

举个例子：假设数组是 [1,2,3]（已经完全归位），遍历到 i=0 时：

x = nums[0] = 1，target_idx = 0；
如果没有 nums[target_idx] != x 的判断，会执行 swap(nums[0], nums[0])（自己和自己交换）；
交换后数组不变，下一次循环还是满足 1≤x≤n，会再次交换 → 无限循环。

而加上 nums[target_idx] != x 后：

nums[0] = 1，nums[target_idx] = nums[0] = 1，此时 1 == 1 → 条件不成立，跳过交换，避免了无意义的循环。

结合具体例子理解

我们用示例 2 nums = [3,4,-1,1] 一步步分析：

第一步：遍历 `i=0`，`nums[i] = 3`

x=3，满足 1≤3≤4（n=4）；
target_idx = 3-1 = 2；
检查 nums[2]（当前是 -1）是否等于 3 → -1 != 3 → 条件成立，需要交换；
交换 nums[0] 和 nums[2] → 数组变为 [-1,4,3,1]。

此时 `i=0` 还没结束（因为是 `while` 循环），现在 `nums[i] = -1`

-1 不满足 1≤x≤4 → while 循环终止，i 自增到 1。

遍历 `i=1`，`nums[i] = 4`

x=4，满足 1≤4≤4；
target_idx = 4-1 = 3；
检查 nums[3]（当前是 1）是否等于 4 → 1 != 4 → 条件成立，交换；
交换 nums[1] 和 nums[3] → 数组变为 [-1,1,3,4]。

此时 `i=1` 仍在 `while` 循环中，现在 `nums[i] = 1`

x=1，满足 1≤1≤4；
target_idx = 1-1 = 0；
检查 nums[0]（当前是 -1）是否等于 1 → -1 != 1 → 条件成立，交换；
交换 nums[1] 和 nums[0] → 数组变为 [1,-1,3,4]。

此时 `i=1` 仍在 `while` 循环中，现在 `nums[i] = -1`

-1 不满足 1≤x≤4 → while 循环终止，i 自增到 2。

遍历 `i=2`，`nums[i] = 3`

x=3，target_idx=2；
检查 nums[2]（就是 3）是否等于 3 → 3 == 3 → 条件不成立，跳过交换。

遍历 `i=3`，`nums[i] = 4`

x=4，target_idx=3；
检查 nums[3]（就是 4）是否等于 4 → 4 == 4 → 条件不成立，跳过交换。

最终数组归位为 [1,-1,3,4]，遍历找第一个 nums[i] != i+1 的位置（i=1，-1≠2），返回 2。

总结这个条件的作用

避免无意义的交换 ：如果数值已经在正确位置上，不需要交换（比如 x=3 已经在索引 2 处）；
避免无限循环：如果没有这个条件，数值会在两个位置之间反复交换（或自己和自己交换），导致程序卡死；
保证归位的正确性：只有当「正确位置上的数不是当前数」时，才需要交换，确保每个数最终能落到自己的位置上。

简单来说，这个条件就是判断「当前数是否已经在正确位置」，只有不在时，才需要交换归位。

🔥矩阵

18🎈. 矩阵置零

关键细节深度解释

1. `ranges::contains` 和 `ranges::fill` 的作用（C++20 特性）

ranges::contains(matrix[0], 0)：等价于「遍历第一行所有元素，判断是否有 0」，替代了手动写 for 循环，代码更简洁；
ranges::fill(matrix[0], 0)：等价于「遍历第一行所有元素，全部赋值为 0」，替代手动循环。

一、核心思路

该解法的核心是利用矩阵自身的第一行和第一列作为标记空间，避免额外开辟 O (m+n) 的存储空间，将空间复杂度优化至 O (1)。核心逻辑：

先记录第一行是否原本包含 0（避免标记过程覆盖原始状态）；
遍历矩阵（从第二行开始），用第一行 / 第一列的元素标记对应行 / 列是否需要置 0；
根据标记对矩阵（除第一行外）置 0；
最后根据初始记录，决定是否将第一行整体置 0。

二、逐行解析

1. 初始化与第一行零标记

cpp 复制代码

int m = matrix.size(), n = matrix[0].size();
bool first_row_has_zero = ranges::contains(matrix[0], 0);

m：矩阵行数，n：矩阵列数；
first_row_has_zero：提前记录第一行是否有 0。关键原因：后续会用第一行作为列的标记位，直接修改第一行的值，因此必须先保存原始状态，否则会丢失第一行是否该置 0 的信息；
ranges::contains：C++20 的范围库函数，等价于遍历matrix[0]判断是否有 0，简化代码。

2. 用第一行 / 列做标记（核心步骤）

cpp 复制代码

for (int i = 1; i < m; i++) 
{
    for (int j = 0; j < n; j++) 
    {
        if (matrix[i][j] == 0) 
        {
            matrix[i][0] = matrix[0][j] = 0;
        }
    }
}

遍历范围：i从 1 开始（跳过第一行，第一行留作标记位），j从 0 到 n-1（覆盖所有列）；
标记规则：如果matrix[i][j] = 0，则：
- matrix[i][0] = 0：标记第i行需要整体置 0；
- matrix[0][j] = 0：标记第j列需要整体置 0；
示例：若matrix[2][3] = 0，则matrix[2][0]和matrix[0][3]都会被设为 0，后续根据这两个标记将第 2 行、第 3 列全部置 0。

3. 根据标记置 0（倒序遍历关键）

cpp 复制代码

for (int i = 1; i < m; i++) 
{
    for (int j = n - 1; j >= 0; j--) 
    {
        if (matrix[i][0] == 0 || matrix[0][j] == 0) 
        {
            matrix[i][j] = 0;
        }
    }
}

遍历范围：仍从第 2 行开始（第一行最后处理）；
核心细节：j 倒序遍历（从 n-1 到 0） ：
- 若正序遍历j（从 0 开始），会先修改matrix[i][0]（第 i 行第 0 列），而matrix[i][0]是第 i 行的标记位，提前修改会导致后续列的判断出错；
- 倒序遍历可避免修改标记位本身，确保所有判断基于原始标记值；
置 0 规则：只要行标记（matrix[i][0]）或列标记（matrix[0][j]）为 0，当前位置就置 0。

4. 处理第一行

cpp 复制代码

if (first_row_has_zero) 
{
    ranges::fill(matrix[0], 0);
}

根据最初记录的first_row_has_zero，若第一行原本有 0，则将第一行全部置 0；
ranges::fill：C++20 范围库函数，等价于遍历matrix[0]将所有元素设为 0，简化代码。

三、关键优势

空间优化：无需额外数组存储行 / 列的零标记，仅用矩阵自身空间，空间复杂度 O (1)；
时间效率：仅需三次遍历矩阵，时间复杂度 O (m*n)（最优复杂度，必须遍历所有元素）；
鲁棒性：通过提前记录第一行状态、倒序遍历列，避免标记位被覆盖导致的错误。

四、示例验证

以矩阵 [[1,1,1],[1,0,1],[1,1,1]] 为例：

初始first_row_has_zero = false（第一行无 0）；
遍历到matrix[1][1] = 0，设置matrix[1][0] = 0、matrix[0][1] = 0；
倒序遍历第 2 行（i=1）：
- j=2：matrix[1][0]=0 → 置 0 → matrix[1][2] = 0；
- j=1：matrix[1][0]=0 → 置 0 → matrix[1][1] = 0；
- j=0：matrix[1][0]=0 → 置 0 → matrix[1][0] = 0；
first_row_has_zero = false，第一行保持不变；
最终矩阵：[[1,0,1],[0,0,0],[1,0,1]]（符合预期）。

为什么要倒着遍历❓

要理解倒序遍历列（j 从 n-1 到 0） 的核心原因，我们需要先明确「标记位的作用」和「正序遍历的风险」，结合具体例子拆解会更清晰。

一、核心前提：标记位的含义

matrix[i][0] 是第 i 行的标记位 （表示第 i 行是否需要整体置 0），在遍历第 i 行的列时，这个标记位的值必须保持原始状态，不能被提前修改。

二、正序遍历的致命问题

假设我们正序遍历 j（从 0 到 n-1），看这个过程会发生什么：

cpp 复制代码

// 错误示例：正序遍历j
for (int i = 1; i < m; i++) {
    for (int j = 0; j < n; j++) { // j从0开始
        if (matrix[i][0] == 0 || matrix[0][j] == 0) {
            matrix[i][j] = 0; // 第一步就修改了matrix[i][0]
        }
    }
}

当 j=0 时：

触发条件 matrix[i][0] == 0（因为这是第 i 行的标记位，本身就是 0）；
执行 matrix[i][0] = 0（看似没变化，但如果标记位原本不是 0，这里会被错误修改）；
更关键的是：如果标记位原本是非 0 （比如第 i 行不需要置 0，但第 j 列需要），正序遍历会先把 matrix[i][0] 改成 0，导致后续 j=1、2... 时，所有列都错误地触发行标记位条件，把整行置 0（而原本只需要置对应列）。

三、倒序遍历的解决思路

倒序遍历 j（从 n-1 到 0），本质是先处理所有非标记位的列，最后处理标记位本身：

cpp 复制代码

// 正确示例：倒序遍历j
for (int i = 1; i < m; i++) {
    for (int j = n-1; j >= 0; j--) { // j从最后一列开始
        if (matrix[i][0] == 0 || matrix[0][j] == 0) {
            matrix[i][j] = 0;
        }
    }
}

遍历过程：

先处理 j=n-1、n-2...1：这些列的判断基于原始的标记位值 （matrix[i][0] 还没被修改），不会出错；
最后处理 j=0：此时所有非标记位的列已经处理完毕，即使修改 matrix[i][0]，也不会影响其他列的判断。

四、具体例子验证

cpp 复制代码

[1, 2, 3]
[0, 5, 6] // i=1行，matrix[1][0]=0（标记位）
[7, 8, 9]

正序遍历 j 的错误结果：

j=0：matrix[1][0] == 0 → 置 0（无变化）；
j=1：matrix[1][0] == 0 → 错误置 0（原本只有 j=0 列需要置 0，现在 j=1 也被置 0）；
j=2：matrix[1][0] == 0 → 错误置 0；
最终第 1 行被全部置 0（错误）。

倒序遍历 j 的正确结果：

j=2：判断 matrix[1][0]==0 → 置 0（符合预期，因为第 1 行需要整体置 0）；
j=1：判断 matrix[1][0]==0 → 置 0（符合预期）；
j=0：判断 matrix[1][0]==0 → 置 0（最后处理标记位，不影响前面的判断）；
最终第 1 行全部置 0（正确，因为标记位本身就表示第 1 行需要置 0）。

再换一个例子（标记位非 0，仅列需要置 0）：矩阵：

cpp 复制代码

[1, 0, 3] // matrix[0][1]=0（第1列标记位）
[4, 5, 6] // i=1行，matrix[1][0]=4（行标记位非0）
[7, 8, 9]

正序遍历 j 的错误结果：

j=0：matrix[1][0]=4 且 matrix[0][0]=1 → 不置 0（正确）；
j=1：matrix[1][0]=4 且 matrix[0][1]=0 → 置 0（正确）；
j=2：matrix[1][0]=4 且 matrix[0][2]=3 → 不置 0（正确）；看似没问题？但如果是这个矩阵：

cpp 复制代码

[1, 0, 3]
[4, 5, 6]
[7, 8, 0] // matrix[2][0]=7（行标记位非0），matrix[0][2]=0（列标记位）

正序遍历 j（i=2 行）：

j=0：matrix[2][0]=7 且 matrix[0][0]=1 → 不置 0（正确）；
j=1：matrix[2][0]=7 且 matrix[0][1]=0 → 置 0（正确）；
j=2：matrix[2][0]=7 且 matrix[0][2]=0 → 置 0（正确）；但如果标记位和列标记叠加，且行标记位原本是 0 但被提前修改：

cpp 复制代码

[1, 0, 3]
[0, 5, 6] // matrix[1][0]=0（行标记位）
[7, 8, 0] // matrix[2][0]=7（行标记位），matrix[0][2]=0（列标记位）

正序遍历 i=2 行 j=0 时：

若此时有其他条件导致 matrix[2][0] 被置 0（比如代码逻辑失误），后续 j=1、2 都会错误置 0；
而倒序遍历从根本上避免了「标记位被提前修改」的风险，无论场景如何，都能保证判断基于原始标记值。

总结

倒序遍历列的核心目的是：在修改标记位（matrix [i][0]）之前，先处理完所有依赖该标记位的列，确保每一列的置 0 判断都基于「原始的标记状态」，而非被修改后的状态，避免逻辑错误。这是该解法中最关键的细节，也是保证算法正确性的核心。

🔥普通数组

13🎈.最大子数组和

一、核心思路：动态规划（DP）

二、代码逐行解析

1. 状态定义

2. 初始化

3. 状态转移（填表）

4. 返回结果

三、示例推演

四、复杂度分析

五、空间优化版（可选）

总结

14🎈. 合并区间

【算法解析：区间合并】

一、核心思路

二、关键细节说明

三、示例演示

四、边界情况处理

总结

15🎈. 轮转数组

完整代码逐行解析

核心函数：my_reverse 解析

1. 模板参数 RandomIt

2. 函数参数 first / last

3. 核心循环逻辑

三、轮转核心逻辑：三次反转

1. 预处理：k = k % n

2. 三次反转的原理（以示例 nums=[1,2,3,4,5,6,7], k=3 为例）

3. 三次反转的代码对应

四、时间 / 空间复杂度

五、边界情况测试

1. k=0（无需轮转）

2. n=1（单元素数组）

3. k=n（轮转 n 步）

4. 示例 2：nums=[-1,-100,3,99], k=2

六、关键易错点提醒

总结

16🎈. 除自身以外数组的乘积

题目背景

核心思路

代码逐行解析

1. 初始化变量

2. 前缀 / 后缀乘积的边界初始化

3. 计算前缀乘积数组 f

4. 计算后缀乘积数组 g

5. 计算最终结果

复杂度分析

17🎈. 缺失的第一个正数

问题分析

代码解释

复杂度分析

先拆解符号含义

为什么需要这个条件？（反过来看更易理解）

结合具体例子理解

第一步：遍历 i=0，nums[i] = 3

此时 i=0 还没结束（因为是 while 循环），现在 nums[i] = -1

遍历 i=1，nums[i] = 4

此时 i=1 仍在 while 循环中，现在 nums[i] = 1

此时 i=1 仍在 while 循环中，现在 nums[i] = -1

遍历 i=2，nums[i] = 3

遍历 i=3，nums[i] = 4

总结这个条件的作用

🔥矩阵

18🎈. 矩阵置零

关键细节深度解释

1. ranges::contains 和 ranges::fill 的作用（C++20 特性）

一、核心思路

二、逐行解析

1. 初始化与第一行零标记

2. 用第一行 / 列做标记（核心步骤）

3. 根据标记置 0（倒序遍历关键）

4. 处理第一行

三、关键优势

四、示例验证

一、核心前提：标记位的含义

二、正序遍历的致命问题

三、倒序遍历的解决思路

四、具体例子验证

正序遍历 j 的错误结果：

核心函数：`my_reverse` 解析

1. 模板参数 `RandomIt`

2. 函数参数 `first` / `last`

1. 预处理：`k = k % n`

2. 三次反转的原理（以示例 `nums=[1,2,3,4,5,6,7], k=3` 为例）

3. 计算前缀乘积数组 `f`

4. 计算后缀乘积数组 `g`

第一步：遍历 `i=0`，`nums[i] = 3`

此时 `i=0` 还没结束（因为是 `while` 循环），现在 `nums[i] = -1`

遍历 `i=1`，`nums[i] = 4`

此时 `i=1` 仍在 `while` 循环中，现在 `nums[i] = 1`

此时 `i=1` 仍在 `while` 循环中，现在 `nums[i] = -1`

遍历 `i=2`，`nums[i] = 3`

遍历 `i=3`，`nums[i] = 4`

1. `ranges::contains` 和 `ranges::fill` 的作用（C++20 特性）